期中真题专项复习03 解答题(含答案)--2024-2025学年八年级数学下册(冀教版)
文档属性
| 名称 | 期中真题专项复习03 解答题(含答案)--2024-2025学年八年级数学下册(冀教版) |  | |
| 格式 | docx | ||
| 文件大小 | 951.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 13:12:58 | ||
图片预览




文档简介
2024-2025学年八年级数学下册(冀教版)
期中真题专项复习03 解答题
一、解答题
1.(2024八下·唐山期中)如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(3,4)、C(4,2),则点B的坐标为 ;
(2)图中格点△ABC的面积为 ;
(3)判断格点△ABC的形状,并说明理由.
2.(2024八下·石家庄期中)如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:
碗的数量(只) 1 2 3 4 5 …
高度 4 5.2 6.4 7.6 8.8 …
(1)用h(cm)表示这摞碗的高度,用x(只)表示这摞碗的数量,求出h与x的函数关系式;
(2)求10个碗的总高度;
(3)若这摞碗的高度为,求这摞碗的数量.
3.(2024八下·唐山期中)在平行四边形中,已知,垂直于,点O是两条对角线的交点,,求的长.
4.(2024八下·承德期中)如图,在中,的平分线交边于点E,若,求的度数.
5.(2024八下·石家庄期中)如图,在平面直角坐标系中,线段的端点为,.
(1)求所在直线的解析式;
(2)某同学设计了一个动画;
在函数中,输入b的值,得到直线,其中点D在x轴上,点C在y轴上.
①当时,则求得两点坐标分别为C(____________),D(____________);
②在输入过程中,若的面积为5,直线就会发蓝光,求此时输入的b值;
③若直线与线段有交点,且交点的横坐标不大于纵坐标时,直线就会发红光,直接写出此时输入的b的取值范围______.
6.(2024八下·栾城期中)为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),其中A组:,B组:,C组:,D组:,E组:,并绘制了如下不完整的统计图.
(1)本次调查一共随机抽取了 名学生的成绩,频数分布直方图中 ,扇形统计图中A组占 %;
(2)补全学生成绩频数分布直方图;
(3)若将竞赛成绩在90分及以上的记为优秀,求优秀学生所在扇形对应圆心角的度数.
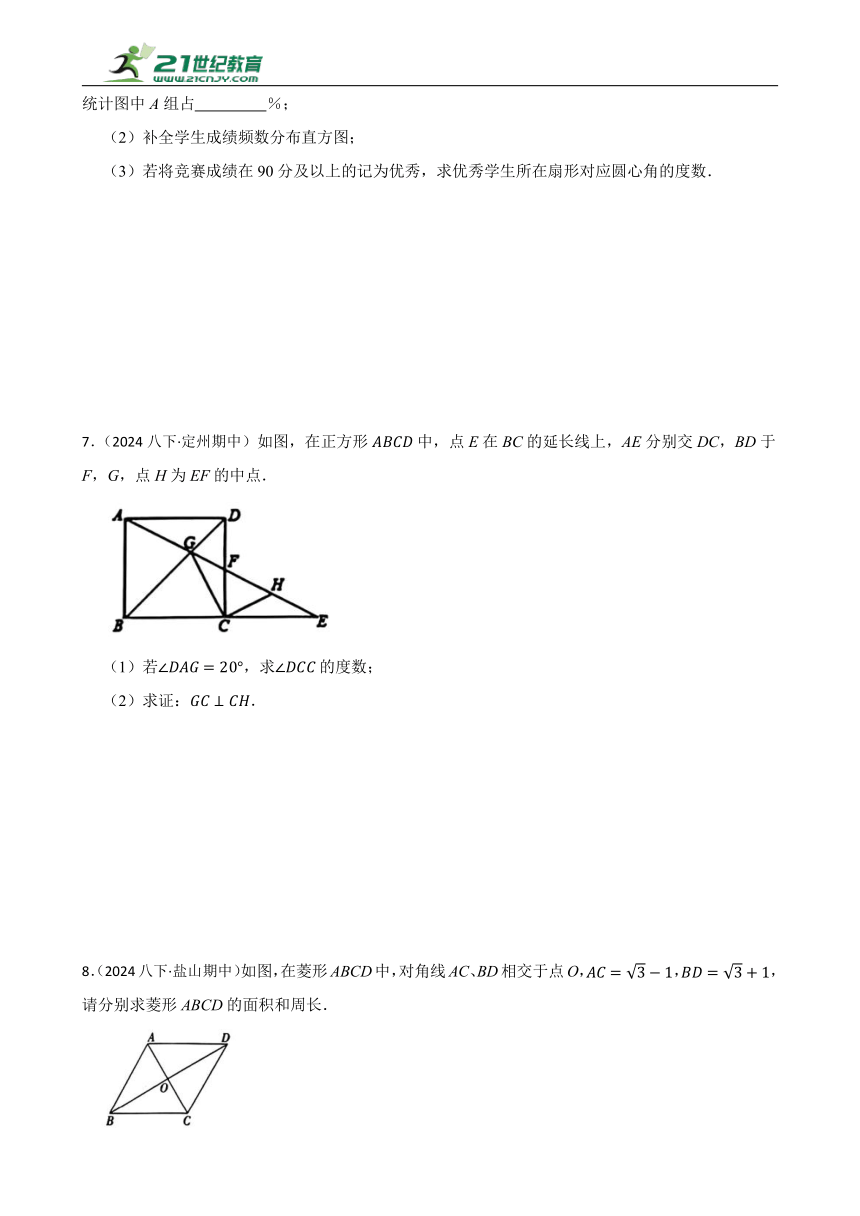
7.(2024八下·定州期中)如图,在正方形中,点E在BC的延长线上,AE分别交DC,BD于F,G,点H为EF的中点.
(1)若,求的度数;
(2)求证:.
8.(2024八下·盐山期中)如图,在菱形ABCD中,对角线AC、BD相交于点O,,,请分别求菱形ABCD的面积和周长.
9.(2024八下·石家庄期中)某专卖店购进两种礼盒进行销售,两种礼盒的进价、售价如表所示.现计划购进两种礼盒共100个,其中种礼盒不少于60个.设购进种礼盒个,两种礼盒全部售完,该专卖店获利元.
进价(元/个) 售价(元/个)
160 220
120 160
(1)求与之间的函数关系式;
(2)若购进100个礼盒的总费用不超过15000元,求最大利润为多少元?
(3)在(2)的条件下,该专卖店对种礼盒以每个优惠元的价格进行优惠促销活动,B种礼盒每个进价、售价保持不变,若最大利润为4900元,则m的值为 .
10.(2024八下·承德期中)数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(阴影部分)”这一推论.
请根据下图完成这个推论的证明过程.
证明:因为
(____________+____________)
由已知条件可得:
_____________=______________
_____________=______________
所以
11.(2024八下·隆化期中)如图,长方形ABCD中,长cm,宽cm,动点P在折线上从A向C移动(点P不与点C重合),设点P运动的路径长为xcm,的面积为cm2.
(1)当点P在AD上运动时,BCP的面积__________,当点P在DC上运动时,BCP的面积__________ (填“增大”“减小”或“不变”)
(2)求y关于x的函数表达式,并指出自变量x的取值范围;
(3)当x为何值时,BCP为等腰三角形.
12.(2024八下·平泉期中)已知矩形沿直线折叠,使点C落在同一平面内处,与交于点E,,求的长.
13.(2024八下·南昌期中)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB边上一点.过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当点D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
14.(2024八下·隆化期中)如图,已知在平面直角坐标系中,直线交x轴于点,交y轴于点.
(1)求直线的函数表达式;
(2)M是x轴上一点,当面积为5时,求点M的坐标.
15.(2024八下·隆化期中)已知点,试分别根据下列条件求出点的坐标.
(1)点在轴上;
(2)点到轴的距离为5,且在第四象限.
(3)若点与轴平行.
16.(2024八下·丰润期中)如图,在四边形中,,,,,、点从点出发沿边以的速度向点移动;同时,点从点出发沿边以的速度向点移动,当一点到达终点时,另一点也随之停止运动,设运动时间为.
(1)______,______(用含的代数式表示);
(2)当两点间的距离是时,求的值;
(3)填空:
当______时,四边形是菱形;
当______时,四边形是矩形.
17.(2024八下·丛台期中)在矩形ABCD中,,,点E是射线BC上一个动点,连接AE并延长交射线DC于点F.将△ABE沿直线AE翻折到△AB'E,延长AB与直线CD交于点M.
(1)求证:;
(2)当点E是边BC的中点时,求CM的长:
(3)当时,求CM的长,
18.(2024八下·丰润期中) 如图,已知 ABCD 对角线AC、BD相交于点 O, 延长CD到点 E, 使CD=DE,连接AE.
(1)求证:四边形ABDE是平行四边形:
(2)连接BE,交AD于点F, 连接OF, 判断CE与OF的数量关系, 并说明理由.
19.(2024八下·遵化期中)平面直角坐标系中,点P的坐标为.
(1)试判断点是否在一次函数的图象上,并说明理由;
(2)如图,一次函数的图象与轴、轴分别相交于点,若点在的内部,求的取值范围.
20.(2024八下·遵化期中)如图,在平面直角坐标系中,过点的直线与直线相交于点,动点在直线上运动.求:
(1)直线的解析式;
(2)当的面积是的面积的时,求出这时点的坐标.
21.(2024八下·遵化期中)如图,在矩形中,,点是上与不重合的任意一点,设,点到的距离为,求出关于自变量的函数关系式,并求出自变量的取值范围.
22.(2024八下·遵化期中)在平面直角坐标系中,已知点与点关于轴对称.
(1)试确定点的坐标.
(2)如果点关于轴的对称点是,求的面积.
23.(2024八下·遵化期中)指出下列关系式中的变量和常量.
(1)球的表面积与球的半径的关系式为.
(2)一物体自高处自由落下,这个物体运动的距离与它下落的时间的关系式为(其中).
24.(2024八下·卢龙期中)如图,一列快车从甲地驶往乙地,-列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲、乙两地之间的距离为 ;
(2)请解释图中点B的实际意义为 ;
(3)求慢车和快车的速度分别是多少?
25.(2024八下·卢龙期中)已知点,分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到两坐标轴的距离相等;
(4)与点的连线平行于x轴.
26.(2024八下·平泉期中)如图,,,,,点是中点、点是中点,点从出发,以每秒个单位的速度沿运动包括点,,,到达点停止,运动时间为.
(1) 、 .
(2)当为什么值时,的面积是.求出值,并简要说明理由.
(3)当为何值时,四边形是平行四边形,说明理由并求此时线段的长.
(4)当点在边上运动时,是等腰三角形,直接写出的值.
27.(2024八下·石家庄期中)某中学举行校庆活动,使用了两架小型无人机进行现场拍摄,1号机所在高度与上升时间的函数图象如图所示;2号机从高度,以的速度上升,两架无人机同时起飞,设2号机所在高度为.
(1)求1号机所在高度与上升时间之间的函数表达式(不必写出的取值范围);
(2)2号机所在高度与上升时间之间的函数表达式为 ,并在图中画出该函数图象(描两点画图象);
(3)在某时刻两架无人机能否位于同一高度?如果能,求此时两架无人机的高度;如果不能,请说明理由.
28.(2024八下·宣化期中)早晨小欣与妈妈同时从家里出发,小欣步行上学、妈妈骑自行车上班,两人的行进方向正好相反,规定从家往学校的方向为正,如图是他们离家的路程(米)与时间(分钟)之间的函数图象.妈妈骑车走了分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为米/分钟,妈妈骑车的速度为米/分钟,并且妈妈与小欣同时到达学校.试回答下列问题:
(1)求、点的坐标;
(2)求的关系式;
(3)求小欣早晨上学需要的时间.
29.(2024八下·定州期中)如图,在中,.BD平分交AC于点D.过D作交AB于点E.交BC于点F.连接EF.
(1)求证:四边形是菱形;
(2)若,,求BF的长.
30.(2024八下·蒸湘期中)如图,直线的图象与轴交于点,直线的图象与轴交于点,两者相交于点.
(1)方程组的解是 ;
(2)当与同时成立时,的取值范围为 ;
(3)在直线的图象上存在异于点的另一点,使得与的面积相等,求出点的坐标.
31.(2024八下·石家庄期中)如图,在中,,,.动点从点出发沿以速度向终点运动,同时点从点出发,以速度沿射线运动,当点到达终点时,点也随之停止运动,设点的运动时间为秒.
(备用图) (备用图)
(1)的长为 cm.
(2)当时,用含的代数式表示线段的长 .
(3)连结.是否存在的值,使得与互相平分?若存在,求出的值;若不存在,请说明理由.
(4)若点关于直线对称的点恰好落在直线上,请直接写出的值.
32.(2024八下·石家庄期中)如图,在中,是的中点,是的中点,过点作,与的延长线相交于点,连接.
(1)求证:四边形是平行四边形;
(2)填空:
①当满足条件时,四边形是 形;
②如果,,,则四边形的面积是 .
答案解析部分
1.(1)(0,0);(2)5 ;(3)直角三角形
2.(1)由表格可知,x每个1只,h个
(2)当时
答:10个碗的总高度为.
(3)当时
答:这摞碗有7个.
根据表格所给数据,写出h与x的函数关系式即可;
(2)把x=10代入一次函数表达式中,求出h的值即可得到10个碗的总高度;
(3)把h=11.2代入一次函数表达式中,求出x的值即可得到答案.
3.
4.
5.(1)直线的解析式为
(2)①
②或
③
6.(1)400;60;5
(2)解:组的人数为:(人),
补全学生成绩频数分布直方图如下:
(3)解:.
答:优秀学生所在扇形对应圆心角的度数为.
(1)本次调查一共随机抽取的学生总人数96÷24%=400(名),
∴B组的人数为:400×15%=60(名),
∴m=60,
∵A组的人数为20人,
∴扇形统计图中A组占的百分比为:×100%=5%,
故答案为:400;60;5.
(1)利用“C”的人数除以对应的百分比可得总人数,再求出“B”的人数,再求出“A”的百分比即可;
(2)先求出“E”的人数,再作出条形统计图即可;
(3)先求出“优秀”的百分比,再乘以360°可得答案.
7.(1)解:四边形是正方形,,,
,,
(2)证明:四边形是正方形,是直角三角形,
点为EF的中点.,,
,,,
由(1)可知,,,.
(1)利用正方形的性质准备条件,根据SAS证明,根据全等三角形的性质即可求解;
(2)由正方形的性质证是直角三角形,根据直角三角形斜边上中线的性质得到 CH=FH,利用角之间的关系求证即可.
8.解:∵在菱形ABCD中,,,
∴菱形ABCD的面积.
,,,
∴,
∴菱形ABCD的周长为.
利用菱形的面积等于对角线乘积的一半求出菱形的面积;再利用勾股定理求出BC的长,最后利用菱形的周长公式求解即可.
9.(1)
(2)由题可列
又 且为整数
y随x而
在中
当时 (元)
(3)8
解:(3)由题有:y=(220-160-m)x+(160-120)(100-x)=(20-m)x+4000,
020-m>0,
y随x的增大而增大,
,
当x=75时,y取最大值,
即4900= (20-m)×75,
解得:m=8,
最大利润为4900元时m的值为8.
故答案为:8.
(1)设购进种礼盒个,则购进B种礼盒(100-x)个,根据总利润=A的利润+B的利润,列出方程整理即可得到答案;
(2)根据购进100个礼盒的总费用不超过15000元,列出不等式求出x≤75,由种礼盒不少于60个,得到,再根据一次函数的性质求解即可;
(3)根据题意得到y=(20-m)x+4000,由010.,;,;,
11.(1)不变;变小;(2);(3)2cm或5cm或8cm
12.
13.(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形.
(1)先证明四边形ADEC是平行四边形,从而得出CE=AD;
(2)首先证明四边形BECD是平行四边形,然后根据直角三角形斜边上的中线的性质得出CD=BD,从而得出四边形BECD是菱形。
14.(1)
(2)M点的坐标为或
15.(1)
(2)
(3)
16.(1),;
(2);
(3); .
17.(1)证明:四边形ABCD是矩形,
,,
由折叠性质可得:
,,
,
(2)点E是边BC的中点,
,
四边形ABCD是矩形,,
,,,
,
,
,
,
设,
,,
在Rt△ADM中,,
,
解得:,CM的长为;
(3)当时,设,应分为
两种情况:
第一种情况,如图,点E在线段BC上,
,,
在Rt△ADM中,,
,
解得:,
CM的长为;
第二种情况,如图,点E在线段BC的延长线上,
,,
在Rt△ADM中,,
,
解得:,
CM的长为21;
综上,当时,CM的长为或21.
(1)根据矩形的性质可得AB∥CD,根据平行线的性质可得∠F=∠BAF,根据折叠的性质可得∠BAF=∠MAF,进而推出∠F=∠MAF,根据等角对等边即可求得;
(2)根据矩形的性质和平行线的性质可得∠F=∠ABF,依据AAS判定△AEB≌△FEC得到AB=CF=6,设CM为x,分别表示出AM,DM,依据勾股定理列出方程,解方程即可求得;
(3)分两种情况:①点E在线段BC上,②点E在线段BC的延长线上,先分别表示出AM,DM,根据勾股定理列出方程,解方程即可求得CM.
18.(1)证明: ∵四边形ABCD 是平行四边形
∴AB=CD,AB∥CD
∵CD = DE
∴AB=DE
∵AB∥DE
∴四边形ABDE是平行四边形
(2)CE=4OF
理由:∵四边形ABCD 是平行四边形,对角线AC、BD相交于点 O
∴O 是BD 的中点
∵四边形ABDE是平行四边形,对角线AD、BE相交于点 F
∴点 F 是 BE 的中点
∴OF是△BDE的中位线
∴2OF=DE
∵CD = DE
∴4OF=CE
(1)先根据平行四边形的性质得到AB=CD,AB∥CD,进而结合题意即可得到AB=DE,再根据平行四边形的判定即可求解;
(2)先根据平行四边形的性质得到O 是BD 的中点,点 F 是 BE 的中点,进而根据三角形的中位线即可得到2OF=DE,从而即可求解。
19.(1)点是否在一次函数的图象上。
理由:当时,,
点在函数图象上;
(2)函数,
当时,,当时,,
点坐标为,点坐标为,
点在的内部,
,,,
.
本题考查一次函数的图象和特征,待定系数法求一次函数的解析式.
(1)要判断点(m+1,m﹣1)是否的函数图象上,将这个点的坐标代入函数解析式,观察等式是否成立可进行判断.
(2)先令和,可求出点坐标和点坐标,再根据题意可列出不等式组:0<m+1<6,0<m﹣1<3,m﹣1<﹣(m+1)+3,解不等式组可求出实数的取值范围.
20.(1)设直线的解析式是,
根据题意得:,解得:,
则直线的解析式是;
(2),当时,,
,,的面积为;
设点的坐标为,,
解得或,
当时,,
当时,,
则点的坐标为或.
本题考查两条直线相交问题,用待定系数法求一次函数的解析式、坐标与图形性质以及三角形面积求法.
(1)设直线的解析式是,将点代入函数解析式可列出方程组,解方程组可求出的值,据此可求出解析式;
(2)当时,可求出点的坐标,利用三角形的面积公式求出的面积,再根据面积公式可求出点的横坐标,再代入解析式可求出点的纵坐标,据此可求出点的坐标.
21.解:连接,如图所示:
为矩形,点是上与不重合的任意一点,
,,
,,,
,点到的距离为,
,整理得,
点是上与不重合的任意一点,即,
又,
,即.
综上所述,有.
本题考查矩形的性质、勾股定理,三角形面积公式.根据矩形的性质可知点是上与、不重合的任意一点,可推出,又,利用等面积法可列出等式,进而可得到关于自变量的函数关系式,再利用勾股定理可求出的长,根据即可求出自变量的取值范围.
22.(1)∵点A(a+b,2﹣a)与点B(a﹣5,b﹣2a)关于y轴对称,
∴,
解得:,
∴点A、B的坐标分别为:(4,1),(﹣4,1);
(2)∵点B关于x轴的对称的点是C,
∴C点坐标为:(﹣4,﹣1),
∴△ABC的面积为:×BC×AB=×2×8=8.
解:(1)∵点A(a+b,2﹣a)与点B(a﹣5,b﹣2a)关于y轴对称,
∴,
解得:,
∴点A、B的坐标分别为:(4,1),(﹣4,1);
(2)∵点B关于x轴的对称的点是C,
∴C点坐标为:(﹣4,﹣1),
∴△ABC的面积为:×BC×AB=×2×8=8.
本题考查平面直角坐标系中,各象限内点的坐标的符号的确定方法,三角形面积求法.
(1)根据在平面直角坐标系中,关于y轴对称时,横坐标为相反数,纵坐标不变,可列出方程组,解方程组可求出a,b,进而求出点的坐标 ;
(2)根据点B关于x轴的对称的点是C,可求出C点坐标,再利用三角形面积公式进行计算可求出答案.
23.(1)关系式为中,变量是,常量是.
(2)关系式为中,变量是,常量是
解:(1)关系式为中,变量是,常量是.
(2)关系式为中,变量是,常量是.
本题考查函数的基本定义.
(1)根据函数的定义: 自变量是在一定取值范围内(定义域)随意取值的变量,据此可确定变量和常量.
(2)根据函数的定义: 自变量是在一定取值范围内(定义域)随意取值的变量,据此可确定变量和常量.
24.(1)900km
(2)当慢车行驶4小时时,慢车和快车相遇;
(3)由图象可知慢车行驶900km,用12h,
∴慢车的速度:900÷12=75(km/h),
∵行驶4小时时,慢车和快车相遇,
∴慢车和快车行驶速度之和为:900÷4=225(km/h),
∴快车的速度:225﹣75=150(km/h),
解:(1)由图像可知甲、乙两地之间的距离为900km;
(2)当两车出发4小时后在B点相遇;
(3)由图象可知慢车行驶900km,用12h,
∴慢车的速度:900÷12=75(km/h),
∵行驶4小时时,慢车和快车相遇,
∴慢车和快车行驶速度之和为:900÷4=225(km/h),
∴快车的速度:225﹣75=150(km/h),
本题考查利用函数的图象解决实际问题.
(1)根据图像可直接找出甲、乙两地之间的距离;
(2)由坐标系中点的意义可得出点B的实际意义 ;
(2)由D点坐标,结合速度=路程÷时间可先求出慢车速度,再由B点坐标可知快、慢车两车速度和,据此可求出快车速度;
25.(1)P(-5.5,0)
(2)P(0,11)
(3)点P的坐标为或(-11,-11)
(4)点P(-4,3)
解:(1)∵点在轴上,
∴,
解得:,
∴,
∴点的坐标为;
(2)∵点在轴上,
∴,
解得:,
∴,
∴点的坐标为;
(3)∵点到两坐标轴的距离相等,
∴,
∴或,
解得:或,
当时,,,
此时点的坐标为;
当时,,,
此时点的坐标为;
综上所述,点的坐标为或;
(4)∵点与点的连线平行于轴,
∴,
解得:,
∴,
∴点的坐标为.
本题考查平面直角坐标系中坐标与图形的性质特点.
(1)根据轴上点的纵坐标为,据此可列出方程,解方程可求出的值,进而写出点P的坐标;
(2)根据轴上点的横坐标为,据此可列出方程,解方程可求出的值,进而写出点P的坐标;
(3)根据点到两坐标轴的距离相等,据此可列出方程,解方程可求出的值,进而写出点P的坐标;;
(4)根据平行于轴上的直线上的点的纵坐标相等据此可列出方程,解方程可求出的值,进而写出点P的坐标;.
26.(1),
(2)或
(3)
(4)或或或
27.(1)解:设与关系式为
将分别代入解得
与关系式为
(2)
(3)若
则
两架无人机可以位于同一高度.高度为9米.
解:(2)由题可得:y2=0.5x+6,
当x=0时,y2=6,当x=6时,y2=9,
该函数图象如下图所示:
故答案为:y2=0.5x+6.
(1)利用待定系数法求直线y1的表达式即可;
(2)根据题意直接写出y2的函数表达式即可;由函数表达式可知该函数结构(0,6),(6,9),画出函数图象即可;
(3)令 ,求出x的值,即可得到两架无人机能位于的同一高度.
28.(1),
(2)
(3)分钟
29.(1)证明:,,四边形是平行四边形.
平分,.,,
,,四边形是菱形
(2)解:,,.
设,则,,
在中,,,
解得,,.
(1)先证四边形BFDE是平行四边形,再根据角平分线的定义和平行线的性质,结合等腰三角形的判定证EB=ED,即可得到平行四边形BFDE是菱形;
(2)设BF=x,于是有DE=BE=x,AE=8﹣x,在RtADE中,由勾股定理可得AE2=DE2+AD2,求出x的值即可.
30.(1)
(2)
(3)解:令,则,
.
点异于点,
,.
.
解:(1)由图象知: 直线与的交点坐标为(2,2) ,
∴ 方程组的解是;
(2)由图象知: 时x>1, 时x<3,
∴与同时成立时的x范围为;
故答案为: .
(1)方程组的解是直线与的交点坐标,据此即得结论;
(2) 分别与时的x范围,再求其公共部分即可;
(3) 设,可得, 据此解答即可.
31.(1)10
(2)
(3)若与互相平分
则四边形是平行四边形
即
当时,与互相平分.
(4)或
解:(1)四边形ABCD是平行四边形, ,
AB=CD=6cm,
,
.
故答案为:10.
(2)由(1)有,CB=10cm,
当点Q刚好运动到点B时,所花时间为10÷8=,
,
点Q必在点B的右侧,
BQ=CQ-CB=8t-10,
故答案为:8t-10.
(4)当点P关于直线AQ对称的点落在线段AB上时,如图所示,
由轴对称的性质可得∠PAQ=∠P'AQ,
BC∥AD,
∠PAQ=∠BQA,
∠P'AQ=∠BQA,
BQ=BA=6cm,
CQ=CB-BQ=10-6=4cm,
8t=4,
解得: ;
当点P关于直线AQ对称的点落在射线BA上时,如图所示,
由轴对称的性质可知:∠1=∠2,
BC∥AD,
∠1=∠3,
∠2=∠4(对顶角相等),
∠4=∠3,
BQ=AB=6cm,
CQ=CB+BQ=10+6=16cm,
8t=16,
解得:t=2.
综上所述, 或.
故答案为:或 .
(1)根据平行四边形的性质得到AB=CD=6cm,再利用勾股定理计算即可;
(2)先证明点Q一定在点B的右侧,再利用线段的和差表示即可;
(3) 若与互相平分,则四边形是平行四边形,根据平行四边形的性质建立方程,解方程即可得到t的值;
(4)分两种情况讨论,当点P关于直线AQ对称的点落在线段AB上时,根据轴对称的性质和平行线的性质证得BQ=BA=6cm,得出CQ的长,即可求解t的值;当点P关于直线AQ对称的点落在射线BA上时,利用平行线的性质和对顶角相等得到BQ=BA=6cm,得出CQ的长,即可求解t的值.
32.(1)证明: ,
又E是AD的中点
又(对顶角相等),
(AAS) ,
且,
四边形AFBD是平行四边形.
(2)矩;1
解:(2)①由(1)有, 四边形AFBD是平行四边形,
,
是等腰三角形,
BD=CD,
AD⊥BC,
∠ADB=90°,
四边形是矩形.
故答案为:矩.
②,,
是等腰直角三角形,
是的中点,
AD⊥BC,
BD=AD=1,
由①可知四边形是矩形,
BD=AD,
四边形是正方形,
四边形的面积=AD2=1.
故答案为:1.
(1)先根据平行线的性质得到,再根据中点的定义得到AE=DE,进而可利用AAS证明,得出AF=CD,则AF=BD,再根据平行四边形的判定方法即可得到结论;
(2)①根据等腰三角形的性质“三线合一”得到AD⊥BC,再结合(1)中结论即可判断四边形是矩形;
②根据等腰直角三角形的性质得到AD⊥BC,进而可证得四边形是正方形,然后根据正方形的面积公式计算即可.
期中真题专项复习03 解答题
一、解答题
1.(2024八下·唐山期中)如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(3,4)、C(4,2),则点B的坐标为 ;
(2)图中格点△ABC的面积为 ;
(3)判断格点△ABC的形状,并说明理由.
2.(2024八下·石家庄期中)如图,把一些相同规格的碗整齐地叠放在水平桌面上,这摞碗的高度随着碗的数量变化而变化的情况如表格所示:
碗的数量(只) 1 2 3 4 5 …
高度 4 5.2 6.4 7.6 8.8 …
(1)用h(cm)表示这摞碗的高度,用x(只)表示这摞碗的数量,求出h与x的函数关系式;
(2)求10个碗的总高度;
(3)若这摞碗的高度为,求这摞碗的数量.
3.(2024八下·唐山期中)在平行四边形中,已知,垂直于,点O是两条对角线的交点,,求的长.
4.(2024八下·承德期中)如图,在中,的平分线交边于点E,若,求的度数.
5.(2024八下·石家庄期中)如图,在平面直角坐标系中,线段的端点为,.
(1)求所在直线的解析式;
(2)某同学设计了一个动画;
在函数中,输入b的值,得到直线,其中点D在x轴上,点C在y轴上.
①当时,则求得两点坐标分别为C(____________),D(____________);
②在输入过程中,若的面积为5,直线就会发蓝光,求此时输入的b值;
③若直线与线段有交点,且交点的横坐标不大于纵坐标时,直线就会发红光,直接写出此时输入的b的取值范围______.
6.(2024八下·栾城期中)为了激发学生的航天兴趣,某校举行了太空科普知识竞赛,竞赛结束后随机抽取了部分学生成绩进行统计,按成绩分为如下5组(满分100分),其中A组:,B组:,C组:,D组:,E组:,并绘制了如下不完整的统计图.
(1)本次调查一共随机抽取了 名学生的成绩,频数分布直方图中 ,扇形统计图中A组占 %;
(2)补全学生成绩频数分布直方图;
(3)若将竞赛成绩在90分及以上的记为优秀,求优秀学生所在扇形对应圆心角的度数.
7.(2024八下·定州期中)如图,在正方形中,点E在BC的延长线上,AE分别交DC,BD于F,G,点H为EF的中点.
(1)若,求的度数;
(2)求证:.
8.(2024八下·盐山期中)如图,在菱形ABCD中,对角线AC、BD相交于点O,,,请分别求菱形ABCD的面积和周长.
9.(2024八下·石家庄期中)某专卖店购进两种礼盒进行销售,两种礼盒的进价、售价如表所示.现计划购进两种礼盒共100个,其中种礼盒不少于60个.设购进种礼盒个,两种礼盒全部售完,该专卖店获利元.
进价(元/个) 售价(元/个)
160 220
120 160
(1)求与之间的函数关系式;
(2)若购进100个礼盒的总费用不超过15000元,求最大利润为多少元?
(3)在(2)的条件下,该专卖店对种礼盒以每个优惠元的价格进行优惠促销活动,B种礼盒每个进价、售价保持不变,若最大利润为4900元,则m的值为 .
10.(2024八下·承德期中)数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线,则所容两长方形面积相等(阴影部分)”这一推论.
请根据下图完成这个推论的证明过程.
证明:因为
(____________+____________)
由已知条件可得:
_____________=______________
_____________=______________
所以
11.(2024八下·隆化期中)如图,长方形ABCD中,长cm,宽cm,动点P在折线上从A向C移动(点P不与点C重合),设点P运动的路径长为xcm,的面积为cm2.
(1)当点P在AD上运动时,BCP的面积__________,当点P在DC上运动时,BCP的面积__________ (填“增大”“减小”或“不变”)
(2)求y关于x的函数表达式,并指出自变量x的取值范围;
(3)当x为何值时,BCP为等腰三角形.
12.(2024八下·平泉期中)已知矩形沿直线折叠,使点C落在同一平面内处,与交于点E,,求的长.
13.(2024八下·南昌期中)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D在AB边上一点.过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当点D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由.
14.(2024八下·隆化期中)如图,已知在平面直角坐标系中,直线交x轴于点,交y轴于点.
(1)求直线的函数表达式;
(2)M是x轴上一点,当面积为5时,求点M的坐标.
15.(2024八下·隆化期中)已知点,试分别根据下列条件求出点的坐标.
(1)点在轴上;
(2)点到轴的距离为5,且在第四象限.
(3)若点与轴平行.
16.(2024八下·丰润期中)如图,在四边形中,,,,,、点从点出发沿边以的速度向点移动;同时,点从点出发沿边以的速度向点移动,当一点到达终点时,另一点也随之停止运动,设运动时间为.
(1)______,______(用含的代数式表示);
(2)当两点间的距离是时,求的值;
(3)填空:
当______时,四边形是菱形;
当______时,四边形是矩形.
17.(2024八下·丛台期中)在矩形ABCD中,,,点E是射线BC上一个动点,连接AE并延长交射线DC于点F.将△ABE沿直线AE翻折到△AB'E,延长AB与直线CD交于点M.
(1)求证:;
(2)当点E是边BC的中点时,求CM的长:
(3)当时,求CM的长,
18.(2024八下·丰润期中) 如图,已知 ABCD 对角线AC、BD相交于点 O, 延长CD到点 E, 使CD=DE,连接AE.
(1)求证:四边形ABDE是平行四边形:
(2)连接BE,交AD于点F, 连接OF, 判断CE与OF的数量关系, 并说明理由.
19.(2024八下·遵化期中)平面直角坐标系中,点P的坐标为.
(1)试判断点是否在一次函数的图象上,并说明理由;
(2)如图,一次函数的图象与轴、轴分别相交于点,若点在的内部,求的取值范围.
20.(2024八下·遵化期中)如图,在平面直角坐标系中,过点的直线与直线相交于点,动点在直线上运动.求:
(1)直线的解析式;
(2)当的面积是的面积的时,求出这时点的坐标.
21.(2024八下·遵化期中)如图,在矩形中,,点是上与不重合的任意一点,设,点到的距离为,求出关于自变量的函数关系式,并求出自变量的取值范围.
22.(2024八下·遵化期中)在平面直角坐标系中,已知点与点关于轴对称.
(1)试确定点的坐标.
(2)如果点关于轴的对称点是,求的面积.
23.(2024八下·遵化期中)指出下列关系式中的变量和常量.
(1)球的表面积与球的半径的关系式为.
(2)一物体自高处自由落下,这个物体运动的距离与它下落的时间的关系式为(其中).
24.(2024八下·卢龙期中)如图,一列快车从甲地驶往乙地,-列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲、乙两地之间的距离为 ;
(2)请解释图中点B的实际意义为 ;
(3)求慢车和快车的速度分别是多少?
25.(2024八下·卢龙期中)已知点,分别根据下列条件求出点P的坐标.
(1)点P在x轴上;
(2)点P在y轴上;
(3)点P到两坐标轴的距离相等;
(4)与点的连线平行于x轴.
26.(2024八下·平泉期中)如图,,,,,点是中点、点是中点,点从出发,以每秒个单位的速度沿运动包括点,,,到达点停止,运动时间为.
(1) 、 .
(2)当为什么值时,的面积是.求出值,并简要说明理由.
(3)当为何值时,四边形是平行四边形,说明理由并求此时线段的长.
(4)当点在边上运动时,是等腰三角形,直接写出的值.
27.(2024八下·石家庄期中)某中学举行校庆活动,使用了两架小型无人机进行现场拍摄,1号机所在高度与上升时间的函数图象如图所示;2号机从高度,以的速度上升,两架无人机同时起飞,设2号机所在高度为.
(1)求1号机所在高度与上升时间之间的函数表达式(不必写出的取值范围);
(2)2号机所在高度与上升时间之间的函数表达式为 ,并在图中画出该函数图象(描两点画图象);
(3)在某时刻两架无人机能否位于同一高度?如果能,求此时两架无人机的高度;如果不能,请说明理由.
28.(2024八下·宣化期中)早晨小欣与妈妈同时从家里出发,小欣步行上学、妈妈骑自行车上班,两人的行进方向正好相反,规定从家往学校的方向为正,如图是他们离家的路程(米)与时间(分钟)之间的函数图象.妈妈骑车走了分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为米/分钟,妈妈骑车的速度为米/分钟,并且妈妈与小欣同时到达学校.试回答下列问题:
(1)求、点的坐标;
(2)求的关系式;
(3)求小欣早晨上学需要的时间.
29.(2024八下·定州期中)如图,在中,.BD平分交AC于点D.过D作交AB于点E.交BC于点F.连接EF.
(1)求证:四边形是菱形;
(2)若,,求BF的长.
30.(2024八下·蒸湘期中)如图,直线的图象与轴交于点,直线的图象与轴交于点,两者相交于点.
(1)方程组的解是 ;
(2)当与同时成立时,的取值范围为 ;
(3)在直线的图象上存在异于点的另一点,使得与的面积相等,求出点的坐标.
31.(2024八下·石家庄期中)如图,在中,,,.动点从点出发沿以速度向终点运动,同时点从点出发,以速度沿射线运动,当点到达终点时,点也随之停止运动,设点的运动时间为秒.
(备用图) (备用图)
(1)的长为 cm.
(2)当时,用含的代数式表示线段的长 .
(3)连结.是否存在的值,使得与互相平分?若存在,求出的值;若不存在,请说明理由.
(4)若点关于直线对称的点恰好落在直线上,请直接写出的值.
32.(2024八下·石家庄期中)如图,在中,是的中点,是的中点,过点作,与的延长线相交于点,连接.
(1)求证:四边形是平行四边形;
(2)填空:
①当满足条件时,四边形是 形;
②如果,,,则四边形的面积是 .
答案解析部分
1.(1)(0,0);(2)5 ;(3)直角三角形
2.(1)由表格可知,x每个1只,h个
(2)当时
答:10个碗的总高度为.
(3)当时
答:这摞碗有7个.
根据表格所给数据,写出h与x的函数关系式即可;
(2)把x=10代入一次函数表达式中,求出h的值即可得到10个碗的总高度;
(3)把h=11.2代入一次函数表达式中,求出x的值即可得到答案.
3.
4.
5.(1)直线的解析式为
(2)①
②或
③
6.(1)400;60;5
(2)解:组的人数为:(人),
补全学生成绩频数分布直方图如下:
(3)解:.
答:优秀学生所在扇形对应圆心角的度数为.
(1)本次调查一共随机抽取的学生总人数96÷24%=400(名),
∴B组的人数为:400×15%=60(名),
∴m=60,
∵A组的人数为20人,
∴扇形统计图中A组占的百分比为:×100%=5%,
故答案为:400;60;5.
(1)利用“C”的人数除以对应的百分比可得总人数,再求出“B”的人数,再求出“A”的百分比即可;
(2)先求出“E”的人数,再作出条形统计图即可;
(3)先求出“优秀”的百分比,再乘以360°可得答案.
7.(1)解:四边形是正方形,,,
,,
(2)证明:四边形是正方形,是直角三角形,
点为EF的中点.,,
,,,
由(1)可知,,,.
(1)利用正方形的性质准备条件,根据SAS证明,根据全等三角形的性质即可求解;
(2)由正方形的性质证是直角三角形,根据直角三角形斜边上中线的性质得到 CH=FH,利用角之间的关系求证即可.
8.解:∵在菱形ABCD中,,,
∴菱形ABCD的面积.
,,,
∴,
∴菱形ABCD的周长为.
利用菱形的面积等于对角线乘积的一半求出菱形的面积;再利用勾股定理求出BC的长,最后利用菱形的周长公式求解即可.
9.(1)
(2)由题可列
又 且为整数
y随x而
在中
当时 (元)
(3)8
解:(3)由题有:y=(220-160-m)x+(160-120)(100-x)=(20-m)x+4000,
0
y随x的增大而增大,
,
当x=75时,y取最大值,
即4900= (20-m)×75,
解得:m=8,
最大利润为4900元时m的值为8.
故答案为:8.
(1)设购进种礼盒个,则购进B种礼盒(100-x)个,根据总利润=A的利润+B的利润,列出方程整理即可得到答案;
(2)根据购进100个礼盒的总费用不超过15000元,列出不等式求出x≤75,由种礼盒不少于60个,得到,再根据一次函数的性质求解即可;
(3)根据题意得到y=(20-m)x+4000,由0
11.(1)不变;变小;(2);(3)2cm或5cm或8cm
12.
13.(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形.
(1)先证明四边形ADEC是平行四边形,从而得出CE=AD;
(2)首先证明四边形BECD是平行四边形,然后根据直角三角形斜边上的中线的性质得出CD=BD,从而得出四边形BECD是菱形。
14.(1)
(2)M点的坐标为或
15.(1)
(2)
(3)
16.(1),;
(2);
(3); .
17.(1)证明:四边形ABCD是矩形,
,,
由折叠性质可得:
,,
,
(2)点E是边BC的中点,
,
四边形ABCD是矩形,,
,,,
,
,
,
,
设,
,,
在Rt△ADM中,,
,
解得:,CM的长为;
(3)当时,设,应分为
两种情况:
第一种情况,如图,点E在线段BC上,
,,
在Rt△ADM中,,
,
解得:,
CM的长为;
第二种情况,如图,点E在线段BC的延长线上,
,,
在Rt△ADM中,,
,
解得:,
CM的长为21;
综上,当时,CM的长为或21.
(1)根据矩形的性质可得AB∥CD,根据平行线的性质可得∠F=∠BAF,根据折叠的性质可得∠BAF=∠MAF,进而推出∠F=∠MAF,根据等角对等边即可求得;
(2)根据矩形的性质和平行线的性质可得∠F=∠ABF,依据AAS判定△AEB≌△FEC得到AB=CF=6,设CM为x,分别表示出AM,DM,依据勾股定理列出方程,解方程即可求得;
(3)分两种情况:①点E在线段BC上,②点E在线段BC的延长线上,先分别表示出AM,DM,根据勾股定理列出方程,解方程即可求得CM.
18.(1)证明: ∵四边形ABCD 是平行四边形
∴AB=CD,AB∥CD
∵CD = DE
∴AB=DE
∵AB∥DE
∴四边形ABDE是平行四边形
(2)CE=4OF
理由:∵四边形ABCD 是平行四边形,对角线AC、BD相交于点 O
∴O 是BD 的中点
∵四边形ABDE是平行四边形,对角线AD、BE相交于点 F
∴点 F 是 BE 的中点
∴OF是△BDE的中位线
∴2OF=DE
∵CD = DE
∴4OF=CE
(1)先根据平行四边形的性质得到AB=CD,AB∥CD,进而结合题意即可得到AB=DE,再根据平行四边形的判定即可求解;
(2)先根据平行四边形的性质得到O 是BD 的中点,点 F 是 BE 的中点,进而根据三角形的中位线即可得到2OF=DE,从而即可求解。
19.(1)点是否在一次函数的图象上。
理由:当时,,
点在函数图象上;
(2)函数,
当时,,当时,,
点坐标为,点坐标为,
点在的内部,
,,,
.
本题考查一次函数的图象和特征,待定系数法求一次函数的解析式.
(1)要判断点(m+1,m﹣1)是否的函数图象上,将这个点的坐标代入函数解析式,观察等式是否成立可进行判断.
(2)先令和,可求出点坐标和点坐标,再根据题意可列出不等式组:0<m+1<6,0<m﹣1<3,m﹣1<﹣(m+1)+3,解不等式组可求出实数的取值范围.
20.(1)设直线的解析式是,
根据题意得:,解得:,
则直线的解析式是;
(2),当时,,
,,的面积为;
设点的坐标为,,
解得或,
当时,,
当时,,
则点的坐标为或.
本题考查两条直线相交问题,用待定系数法求一次函数的解析式、坐标与图形性质以及三角形面积求法.
(1)设直线的解析式是,将点代入函数解析式可列出方程组,解方程组可求出的值,据此可求出解析式;
(2)当时,可求出点的坐标,利用三角形的面积公式求出的面积,再根据面积公式可求出点的横坐标,再代入解析式可求出点的纵坐标,据此可求出点的坐标.
21.解:连接,如图所示:
为矩形,点是上与不重合的任意一点,
,,
,,,
,点到的距离为,
,整理得,
点是上与不重合的任意一点,即,
又,
,即.
综上所述,有.
本题考查矩形的性质、勾股定理,三角形面积公式.根据矩形的性质可知点是上与、不重合的任意一点,可推出,又,利用等面积法可列出等式,进而可得到关于自变量的函数关系式,再利用勾股定理可求出的长,根据即可求出自变量的取值范围.
22.(1)∵点A(a+b,2﹣a)与点B(a﹣5,b﹣2a)关于y轴对称,
∴,
解得:,
∴点A、B的坐标分别为:(4,1),(﹣4,1);
(2)∵点B关于x轴的对称的点是C,
∴C点坐标为:(﹣4,﹣1),
∴△ABC的面积为:×BC×AB=×2×8=8.
解:(1)∵点A(a+b,2﹣a)与点B(a﹣5,b﹣2a)关于y轴对称,
∴,
解得:,
∴点A、B的坐标分别为:(4,1),(﹣4,1);
(2)∵点B关于x轴的对称的点是C,
∴C点坐标为:(﹣4,﹣1),
∴△ABC的面积为:×BC×AB=×2×8=8.
本题考查平面直角坐标系中,各象限内点的坐标的符号的确定方法,三角形面积求法.
(1)根据在平面直角坐标系中,关于y轴对称时,横坐标为相反数,纵坐标不变,可列出方程组,解方程组可求出a,b,进而求出点的坐标 ;
(2)根据点B关于x轴的对称的点是C,可求出C点坐标,再利用三角形面积公式进行计算可求出答案.
23.(1)关系式为中,变量是,常量是.
(2)关系式为中,变量是,常量是
解:(1)关系式为中,变量是,常量是.
(2)关系式为中,变量是,常量是.
本题考查函数的基本定义.
(1)根据函数的定义: 自变量是在一定取值范围内(定义域)随意取值的变量,据此可确定变量和常量.
(2)根据函数的定义: 自变量是在一定取值范围内(定义域)随意取值的变量,据此可确定变量和常量.
24.(1)900km
(2)当慢车行驶4小时时,慢车和快车相遇;
(3)由图象可知慢车行驶900km,用12h,
∴慢车的速度:900÷12=75(km/h),
∵行驶4小时时,慢车和快车相遇,
∴慢车和快车行驶速度之和为:900÷4=225(km/h),
∴快车的速度:225﹣75=150(km/h),
解:(1)由图像可知甲、乙两地之间的距离为900km;
(2)当两车出发4小时后在B点相遇;
(3)由图象可知慢车行驶900km,用12h,
∴慢车的速度:900÷12=75(km/h),
∵行驶4小时时,慢车和快车相遇,
∴慢车和快车行驶速度之和为:900÷4=225(km/h),
∴快车的速度:225﹣75=150(km/h),
本题考查利用函数的图象解决实际问题.
(1)根据图像可直接找出甲、乙两地之间的距离;
(2)由坐标系中点的意义可得出点B的实际意义 ;
(2)由D点坐标,结合速度=路程÷时间可先求出慢车速度,再由B点坐标可知快、慢车两车速度和,据此可求出快车速度;
25.(1)P(-5.5,0)
(2)P(0,11)
(3)点P的坐标为或(-11,-11)
(4)点P(-4,3)
解:(1)∵点在轴上,
∴,
解得:,
∴,
∴点的坐标为;
(2)∵点在轴上,
∴,
解得:,
∴,
∴点的坐标为;
(3)∵点到两坐标轴的距离相等,
∴,
∴或,
解得:或,
当时,,,
此时点的坐标为;
当时,,,
此时点的坐标为;
综上所述,点的坐标为或;
(4)∵点与点的连线平行于轴,
∴,
解得:,
∴,
∴点的坐标为.
本题考查平面直角坐标系中坐标与图形的性质特点.
(1)根据轴上点的纵坐标为,据此可列出方程,解方程可求出的值,进而写出点P的坐标;
(2)根据轴上点的横坐标为,据此可列出方程,解方程可求出的值,进而写出点P的坐标;
(3)根据点到两坐标轴的距离相等,据此可列出方程,解方程可求出的值,进而写出点P的坐标;;
(4)根据平行于轴上的直线上的点的纵坐标相等据此可列出方程,解方程可求出的值,进而写出点P的坐标;.
26.(1),
(2)或
(3)
(4)或或或
27.(1)解:设与关系式为
将分别代入解得
与关系式为
(2)
(3)若
则
两架无人机可以位于同一高度.高度为9米.
解:(2)由题可得:y2=0.5x+6,
当x=0时,y2=6,当x=6时,y2=9,
该函数图象如下图所示:
故答案为:y2=0.5x+6.
(1)利用待定系数法求直线y1的表达式即可;
(2)根据题意直接写出y2的函数表达式即可;由函数表达式可知该函数结构(0,6),(6,9),画出函数图象即可;
(3)令 ,求出x的值,即可得到两架无人机能位于的同一高度.
28.(1),
(2)
(3)分钟
29.(1)证明:,,四边形是平行四边形.
平分,.,,
,,四边形是菱形
(2)解:,,.
设,则,,
在中,,,
解得,,.
(1)先证四边形BFDE是平行四边形,再根据角平分线的定义和平行线的性质,结合等腰三角形的判定证EB=ED,即可得到平行四边形BFDE是菱形;
(2)设BF=x,于是有DE=BE=x,AE=8﹣x,在RtADE中,由勾股定理可得AE2=DE2+AD2,求出x的值即可.
30.(1)
(2)
(3)解:令,则,
.
点异于点,
,.
.
解:(1)由图象知: 直线与的交点坐标为(2,2) ,
∴ 方程组的解是;
(2)由图象知: 时x>1, 时x<3,
∴与同时成立时的x范围为;
故答案为: .
(1)方程组的解是直线与的交点坐标,据此即得结论;
(2) 分别与时的x范围,再求其公共部分即可;
(3) 设,可得, 据此解答即可.
31.(1)10
(2)
(3)若与互相平分
则四边形是平行四边形
即
当时,与互相平分.
(4)或
解:(1)四边形ABCD是平行四边形, ,
AB=CD=6cm,
,
.
故答案为:10.
(2)由(1)有,CB=10cm,
当点Q刚好运动到点B时,所花时间为10÷8=,
,
点Q必在点B的右侧,
BQ=CQ-CB=8t-10,
故答案为:8t-10.
(4)当点P关于直线AQ对称的点落在线段AB上时,如图所示,
由轴对称的性质可得∠PAQ=∠P'AQ,
BC∥AD,
∠PAQ=∠BQA,
∠P'AQ=∠BQA,
BQ=BA=6cm,
CQ=CB-BQ=10-6=4cm,
8t=4,
解得: ;
当点P关于直线AQ对称的点落在射线BA上时,如图所示,
由轴对称的性质可知:∠1=∠2,
BC∥AD,
∠1=∠3,
∠2=∠4(对顶角相等),
∠4=∠3,
BQ=AB=6cm,
CQ=CB+BQ=10+6=16cm,
8t=16,
解得:t=2.
综上所述, 或.
故答案为:或 .
(1)根据平行四边形的性质得到AB=CD=6cm,再利用勾股定理计算即可;
(2)先证明点Q一定在点B的右侧,再利用线段的和差表示即可;
(3) 若与互相平分,则四边形是平行四边形,根据平行四边形的性质建立方程,解方程即可得到t的值;
(4)分两种情况讨论,当点P关于直线AQ对称的点落在线段AB上时,根据轴对称的性质和平行线的性质证得BQ=BA=6cm,得出CQ的长,即可求解t的值;当点P关于直线AQ对称的点落在射线BA上时,利用平行线的性质和对顶角相等得到BQ=BA=6cm,得出CQ的长,即可求解t的值.
32.(1)证明: ,
又E是AD的中点
又(对顶角相等),
(AAS) ,
且,
四边形AFBD是平行四边形.
(2)矩;1
解:(2)①由(1)有, 四边形AFBD是平行四边形,
,
是等腰三角形,
BD=CD,
AD⊥BC,
∠ADB=90°,
四边形是矩形.
故答案为:矩.
②,,
是等腰直角三角形,
是的中点,
AD⊥BC,
BD=AD=1,
由①可知四边形是矩形,
BD=AD,
四边形是正方形,
四边形的面积=AD2=1.
故答案为:1.
(1)先根据平行线的性质得到,再根据中点的定义得到AE=DE,进而可利用AAS证明,得出AF=CD,则AF=BD,再根据平行四边形的判定方法即可得到结论;
(2)①根据等腰三角形的性质“三线合一”得到AD⊥BC,再结合(1)中结论即可判断四边形是矩形;
②根据等腰直角三角形的性质得到AD⊥BC,进而可证得四边形是正方形,然后根据正方形的面积公式计算即可.
同课章节目录
