期中真题专项复习02 填空题(含答案)--2024-2025学年八年级数学下册(冀教版)
文档属性
| 名称 | 期中真题专项复习02 填空题(含答案)--2024-2025学年八年级数学下册(冀教版) |  | |
| 格式 | docx | ||
| 文件大小 | 814.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 13:28:27 | ||
图片预览


文档简介
2024-2025学年八年级数学下册(冀教版)
期中真题专项复习02 填空题
一、填空题
1.(2024八下·石家庄期中)点关于x轴对称的点的坐标是 .
2.(2024八下·唐山期中)如图,在矩形ABCD中,,以点B为圆心,BC长为半径画弧,交边AD于点E,若AE·ED=,则矩形ABCD的面积为 .
3.(2024八下·承德期中)实验探究:如图所示,对折矩形纸片,使与重合,得到折痕,把纸片展平;再一次折叠纸片,使点落在上,并使折痕经过点,得到折痕,同时得到线段,.请你观察如图,猜想等于 .
4.(2021八下·罗平期中)如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件 (只添一个即可),使四边形ABCD是平行四边形
5.(2019八下·卢龙期中)在函数y= 中,自变量x的取值范围是 .
6.(2024八下·隆化期中)如图,在平面直角坐标系xOy中,直线与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交点交于点D,则点C的坐标为 ,点D的坐标为 .
7.(2024八下·丰润期中) 如图, 菱形 ABCD 的边长为. ,对角线AC, BD交于点 O, OA=1, 则菱形ABCD的面积为 .
8.(2024八下·遵化期中)已知一次函数的图象经过点且和直线平行,则该函数的表达式为 .
9.(2024八下·遵化期中)已知点和点关于轴对称,那么 .
10.(2024八下·卢龙期中)某市地铁票价计费标准如表所示:乘车距离x(单位:公里)
乘车距离x
票价(元) 3 4 5 6 每增加1元可乘20公里
另外,使用市政交通一卡通,每个自然月每张卡片支出累计满100元后,超出部分打8折;满150元后,超出部分打5折;支出累计达400元后,不再打折.小红妈妈上班时,需要乘坐地铁15公里到达公司,每天上下班共乘坐两次,如果每次乘坐地铁都使用市政交通一卡通,那么每月第22次乘坐地铁上下班时,她刷卡支出的费用是 元.
11.(2024八下·卢龙期中)点在第-象限,且到y轴的距离为3,直线轴,且.则点C的坐标为 .
12.(2024八下·卢龙期中)点与点关于y轴对称,则的值为 .
13.(2024八下·卢龙期中)剧院里1排5号可以用表示,则表示 .
14.(2024八下·庐江期中)如图所示,平行四边形ABCD中,顶点A、B、D在坐标轴上,AD=5,AB=9,点A的坐标为(﹣3,0),则点C的坐标为
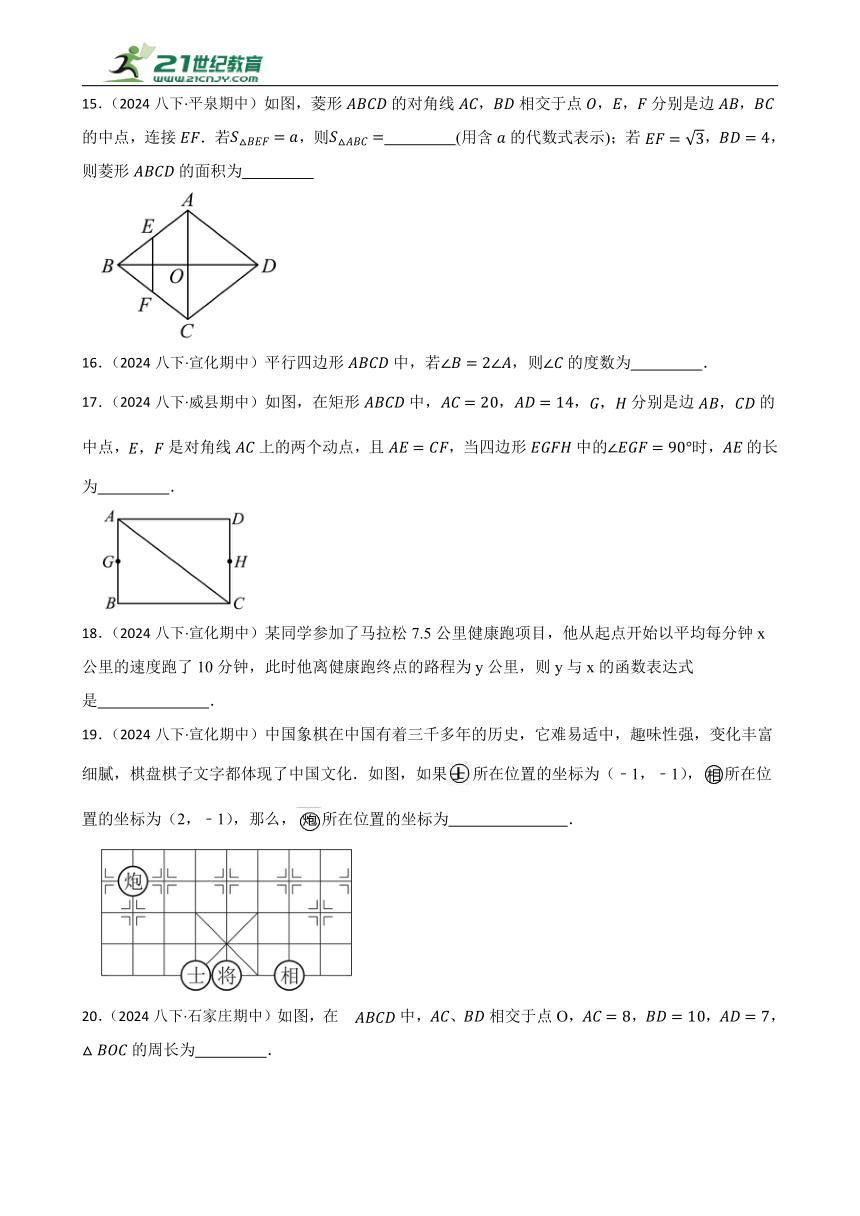
15.(2024八下·平泉期中)如图,菱形的对角线,相交于点,,分别是边,的中点,连接.若,则 (用含的代数式表示);若,,则菱形的面积为
16.(2024八下·宣化期中)平行四边形中,若,则的度数为 .
17.(2024八下·威县期中)如图,在矩形中,,,分别是边的中点,是对角线上的两个动点,且,当四边形中的时,的长为 .
18.(2024八下·宣化期中)某同学参加了马拉松7.5公里健康跑项目,他从起点开始以平均每分钟x公里的速度跑了10分钟,此时他离健康跑终点的路程为y公里,则y与x的函数表达式是 .
19.(2024八下·宣化期中)中国象棋在中国有着三千多年的历史,它难易适中,趣味性强,变化丰富细腻,棋盘棋子文字都体现了中国文化.如图,如果所在位置的坐标为(﹣1,﹣1),所在位置的坐标为(2,﹣1),那么,所在位置的坐标为 .
20.(2024八下·石家庄期中)如图,在中,、相交于点O,,,,的周长为 .
21.(2024八下·澧县期中)如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
22.(2024八下·澧县期中)如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .
23.(2024八下·定州期中)如图,在中,,为边BC上一动点(且点P不与点B、C重合),于,于.则EF的最小值为 .
24.(2024八下·定州期中)如图,在平面直角坐标系中,四边形是菱形.若点A的坐标是.则菱形的周长为 .
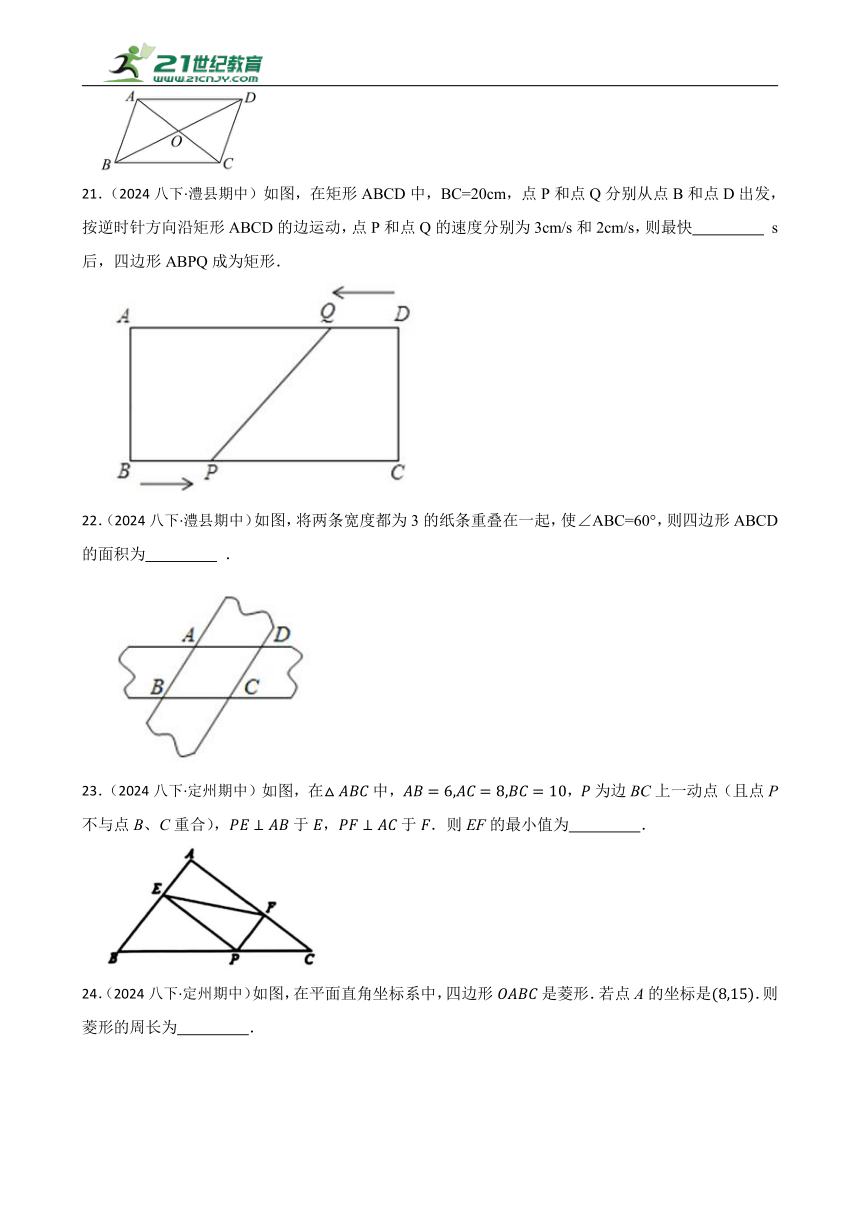
25.(2024八下·定州期中)如图,矩形中,,两条对角线AC、BD所夹的钝角为120°,则BC的长为 .
26.(2024八下·定州期中)如图,在中,D、E分别为AB和AC中点,若,则DE的长为 .
27.(2024八下·盐山期中)如图,E,F分别是的边AB,CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若的面积为2,的面积为4,的面积为26,则阴影部是的面积为 .
28.(2024八下·盐山期中)如图,在矩形ABCD中,对角线AC、BD相交于点O.已知,,则BC的长为 .
29.(2024八下·丰润期中)如图,菱形的边长为,对角线交于点,,则菱形的面积为 .
30.(2024八下·石家庄期中)如图,在平面直角坐标系中,放置一平面镜,其中点的坐标分别为,,从点发射光线,其图象对应的函数解析式为.
①若入射光线与平面镜有公共点,的取值范围是 .
②规定横坐标与纵坐标均为整数的点是整点,光线经过镜面反射后,反射光线与轴相交于点,点是整点的个数是 .
31.(2024八下·石家庄期中)在周长为600米的三角形地块中修建如图所示的三条水渠,则水渠的总长为 米.
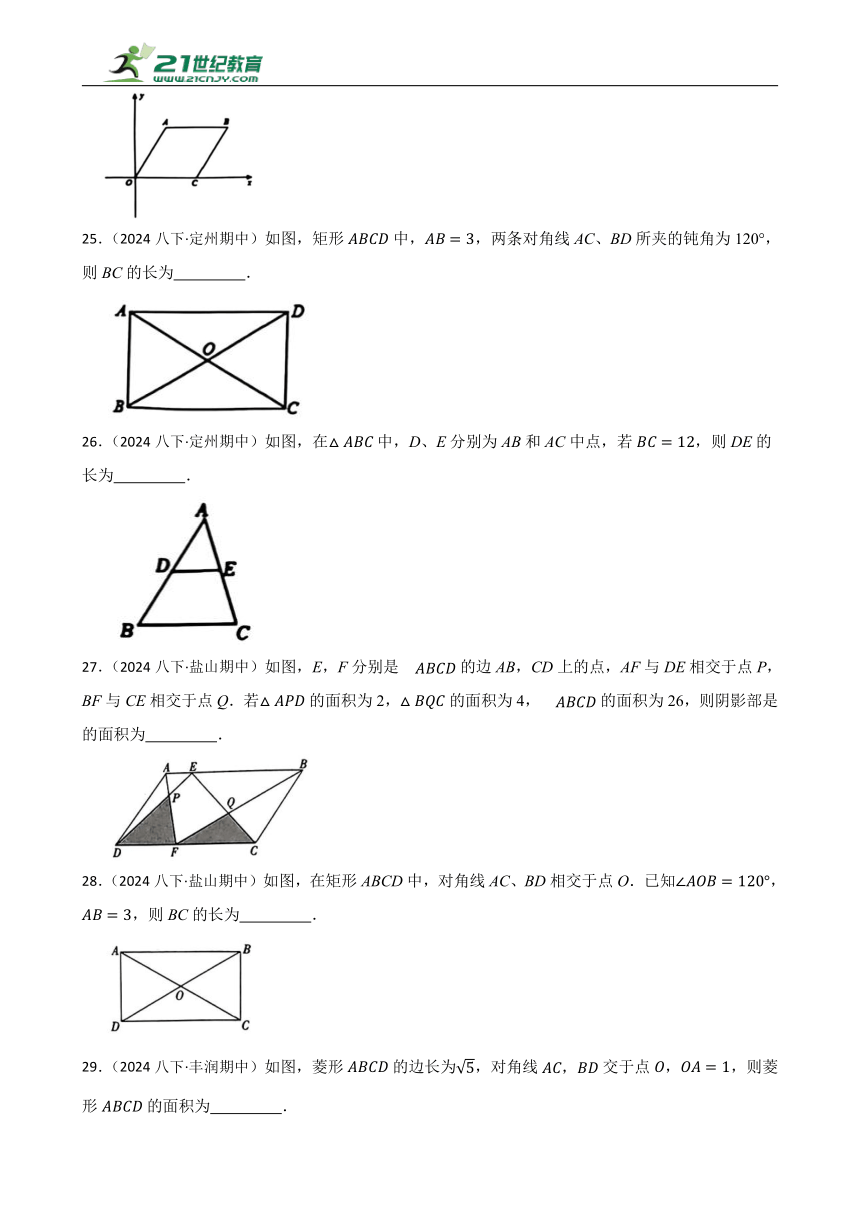
32.(2024八下·邯郸经济技术开发期中)在学习《坐标与图形的位置》的课堂上,老师让同学们自主编题,小刚同学编的题目是:“已知正方形ABCD(边长自定),请建立适当的平面直角坐标系,确定正方形ABCD各顶点的坐标”.同桌小华同学按题目要求建立了平面直角坐标系并正确的写出了正方形各顶点的坐标,若在小华同学建立的平面直角坐标系中,正方形ABCD关于x轴对称,但不关于y轴对称,点A的坐标为,则点C的坐标为 .
33.(2024八下·邯郸经济技术开发期中)某水果销售商有100千克苹果,当苹果单价为15元/千克时,能全部销售完,市场调查表明苹果单价每提高1元,销售量减少6千克,若苹果单价提高x元,则苹果销售额y关于x的函数表达式为 .
34.(2024八下·邯郸经济技术开发期中)小明在教室中的座位为第3行第6列,记为,小亮在第5行第1列,记为 .
35.(2024八下·石家庄期中)已知,点P在一次函数的图象上,且到y轴的距离为3,则点P的坐标为 .
36.(2024八下·武邑期中)如图,矩形的对角线的垂直平分线交于点E,交于点F.连接,,若,,则的长为.
37.(2024八下·武邑期中)若在四边形中,的长度之比是,则四边形是平行四边形,判定的依据是.
38.(2024八下·阜平期中) 如图,在矩形中,,,分别是边的中点,是对角线上的两个动点,且,当四边形中的时,的长为 .
39.(2024八下·阜平期中) 如图,某小区要在一块空地上围一个四边形花坛,,分别是边,的中点,且米,则的长为 米.
40.(2024八下·路南期中)四边形ABCD是边长为4的正方形,点E在线段AD上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF,如图,当时,则 .
41.(2024八下·任泽期中)如图,在菱形纸片中,.
(1) .
(2)点E在边上,将菱形纸片沿折叠,点C对应点为点,且是的垂直平分线,则的大小为 .
42.(2024八下·大渡口期中)已知点B的坐标为,它向右平移4个单位长度,再向上平移2个单位长度,得到点,则点的坐标为 .
43.(2024八下·安次期中)如图,在平面直角坐标系中,已知点,以点O为圆心,的长为半径画弧,交网格线于点,则①的长为.②a的值是.
44.(2024八下·雄安期中)如图1,E,F分别为矩形纸带的边上的点,,将纸带沿折叠成图2(G为和的交点),则 ;再沿折叠成图3(H为和的交点),则图3中的 .
45.(2024八下·邢台期中)在平面直角坐标系中,已知,点与点关于轴对称,,则的面积为 .
46.(2024八下·邢台期中)某班学生参加学校组织的“垃圾分类”知识竞赛,将学生成绩制成如图所示的频数分布直方图(每组数据包括左端值不包括右端值),其中成绩为“优良”(80分及80分以上)的学生所占百分比为 .
47.(2024八下·献县期中)如图,在菱形中,,,E为边的中点,连接BE,则菱形的面积等于 ,的长等于 .
48.(2024八下·三河期中)如图,在矩形中,,分别是边,上的动点,是线段的中点,,,,为垂足,连接.若,,,则的最小值是 .
49.(2024八下·顺平期中)将形状、大小相同的两个矩形,如图摆放,已知,在边上找一点F,使得,连接.若,则 .
50.(2024八下·昌黎期中)门卫保安老张在校门口观察马路上车辆通行情况,观察了10分钟,其间共有50辆车通过.其中自行车5辆,电动车25辆,汽车20辆,在这段时间内,电动车通过的频率是 .
答案解析部分
1.
2.5
3.
4.BO=DO
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形.
故答案为:BO=DO.
根据题目条件结合平行四边形的判定方法:对角线互相平分的四边形是平行四边形分别进行分析即可.
5.x≥1
解:根据题意得:x﹣1≥0,
解得:x≥1.
故答案为:x≥1.
因为当函数表达式是二次根式时,被开方数为非负数,所以x﹣1≥0,解不等式可求x的范围.
6.(-1,0);(0,)
7.4
解:∵四边形为菱形,边长为,
∴,,,,
∴,
∴,
∴,
∴菱形的面积为,
故答案为:
先根据菱形的性质得到,,,,进而运用勾股定理求出OB,从而得到BD,再根据菱形的面积公式即可求解。
8.
解:由一次函数y=kx+b的图象平行于直线y=2x﹣3,可知k=2
则一次函数为y=2x+b,
将A的坐标(1,3)代入,得:2+b=3,
解得:b=1
这个一次函数的解析式是y=2x+1.
故答案为:y=2x+1.
本题考查待定系数法求一次函数解析式.根据两直线平行可得k=2,可得直线解析式为y=2x+b,将点A(1,3)代入解析式可求出b的值,据此可求出直线解析式.
9.10
解:点和点关于轴对称,
,,
.
故答案为:10.
本题考查关于轴对称的点的坐标.根据关于轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数.据此可求出的值,据此可求出答案.
10.4
解:小红妈妈每天的上下班的费用分别为5元,即每天10元,10天后花费100元,第22次乘坐地铁时,价格给予8折优惠,此时花费5×0.8=4元,
故答案为:4.
本题考查分段函数的应用问题.根据优惠方案,分别计算每次乘车的费用,再进行累计可求出答案.
11.(3,7)或(3,1)
解:∵点在第一象限,且到轴的距离为,
∴,
∵直线轴,
∴点的横坐标为,
又∵,
∴点的纵坐标为或,
∴点的坐标为或.
故答案为:或.
本题考查坐标与图形的性质.根据点的特征,可求出点的坐标,再根据轴可确定点横坐标,再根据可确定点的纵坐标.分两种情况可写出点的坐标.
12.1
解:∵点与点关于轴对称,
∴,,
解得:,,
∴.
故答案为:.
本题考查关于轴,轴对称的点的坐标特征.根据平面直角坐标系中两点关于轴对称的特征:纵坐标相同,横坐标互为相反,可列出方程组,解方程组可求出,的值,据此可求出式子的值.
13.6排2号
解:∵影院里1排5号可以用表示,
∴表示的是6排2号.
故答案为:6排2号.
本题考查坐标确定位置.根据题意可得,第一个数表示排,第二个数表示号,将有序数对转化为位置问题,可选出答案.
14.(9,4)
解:∵四边形ABCD是平行四边形,
∴CD=AB=9,
∵点A的坐标为(﹣3,0),
∴OA=3,
∴OD==4,
∴点C的坐标为(9,4).
故答案为:(9,4).
由平行四边形的性质得出CD=AB=9,由勾股定理求出OD,即可得出点C的坐标.
15.;
16.60°
17.3或17
18.
19.(﹣3,2)
20.16
21.4
解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
根据矩形的性质,可得BC与AD的关系,根据矩形的判定定理,可得BP=AQ,根据解题元一次方程,可得答案.
22.6
解:∵纸条的对边平行,即AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵两张纸条的宽度都是3,
∴S四边形ABCD=AB×3=BC×3,
∴AB=BC,
∴平行四边形ABCD是菱形,即四边形ABCD是菱形.
如图,过A作AE⊥BC,垂足为E,
∵∠ABC=60°,
∴∠BAE=90°﹣60°=30°,
∴AB=2BE,
在△ABE中,AB2=BE2+AE2,
即AB2=AB2+32,
解得AB=2,
∴S四边形ABCD=BC AE=2×3=6.
故答案是:6.
先根据两组对边分别平行证明四边形ABCD是平行四边形,再根据两张纸条的宽度相等,利用面积求出AB=BC,然后根据邻边相等的平行四边形是菱形;根据宽度是3cm与∠ABC=60°求出菱形的边长,然后利用菱形的面积=底×高计算即可.
23.4.8
解:连接
∵,,
∴
∴
∴是直角三角形,
又∵,
∴四边形是矩形
∴
∵当时,有最小值
∴最小
∴
∴
∴
∴
故答案为:.
连接AP,根据勾股定理的逆定理证是直角三角形;根据三个角是直角的四边形是矩形判定四边形AEPF是矩形,得EF=AP;当AP垂直BC时,AP有最小值,故EF最小;根据三角形的面积公式,求出AP,即EF的值.
24.68
解:如图所示,过A作轴于点E,
∵点A的坐标是
∴,
∴
∵四边形是菱形,
∴,
∴菱形的周长.
故答案为:68.
过A作AE⊥x轴于点E,利用勾股定理求出OA的长即可.
25.
解:四边形是矩形,
,,,
,
,
,
是等边三角形,
,
,
,
∴.
故答案为:.
根据矩形的性质证等边三角形AOB,根据等边三角形的性质,结合勾股定理求解.
26.6
解:∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
又BC=12,
∴,
故答案为:6.
三角形的中位线平行于第三边,并且等于第三边的一半,据此求解。
27.7
连接EF,过点E作EM⊥DC于点M,如图所示:
∵S△DEC=DC×EM,S平行四边形ABCD=DC×EM=26,
∴S△DEC=×26=13,
∵四边形ABCD是平行四边形,
∴AB//CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,S△EFQ=S△BCQ,S△EFD=S△ADF,
∴S△EFP=S△ADP,S△APD=2S△APD=2,S△BQC=4,
∴S四边形EPFQ=2+4=6,
∴S阴影=S△DEC-S四边形EPFQ=13-6=7,
故答案为:7.
连接EF,过点E作EM⊥DC于点M,先求出S△EFP=S△ADP,S△APD=2S△APD=2,S△BQC=4,再利用割补法求出S阴影=S△DEC-S四边形EPFQ=13-6=7即可.
28.
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OD,
∵∠AOB=120°,
∴∠AOD=60°,
∴△AOD是等边三角形,
∴∠ADO=60°,∠BAC=30°,
∴AC=2BC,
∴4BC2=BC2+9,
解得:BC=,
故答案为:.
先证出△AOD是等边三角形,可得∠ADO=60°,∠BAC=30°,再结合4BC2=BC2+9,求出BC的长即可.
29.
30.;7
解:①当入射光线刚好经过点A(4,2)时,
得2=4n+n,
解得:n=;
当入射光线刚好经过点B(4,6)时,
得6=4n+n,
解得:n=,
入射光线与平面镜有公共点,的取值范围是.
故答案为:.
②如图所示,作出点C关于AB的对称点C',作直线AC'、BC'分别交y轴于点E1、E2,
C(-1,0),A(4,2),
C'坐标为(9,0),
设直线AC'的表达式为y1=kx+b(k≠0),
把A(4,2),C'(9,0)代入y1=kx+b(k≠0),
得,
解得:,
直线AC'的表达式为,
设直线BC'的表达式为y2=ax+c(a≠0),
把B(4,6),C'(9,0)代入y2=ax+c(a≠0),
得,
解得:,
直线BC'的表达式为,
当x=0时,,,
即点E1(0,),点E2(0,),
点整点有:4,5,6,7,8,9,10,共7个.
故答案为:7.
①利用待定系数法分别求出直线AC和直线BC的表达式即可得到n的取值范围;
②作出点C关于AB的对称点C',作直线AC'、BC'分别交y轴于点E1、E2,先根据轴对称的性质求出点C'的坐标,再利用待定系数法分别求出AC',BC'的表达式,进而得到AC',BC'于y轴的交点坐标,根据点E的坐标在此范围内即可得到答案.
31.300
解:如图所示,
点D、E、F分别是AB、BC、CD的中点,
DF、DE、EF都是的中位线,
的周长是600米,
BC+AC+AB=600米,
米,
水渠的总长为300米.
故答案为:300.
先证明DF、DE、EF都是的中位线,进而得到再根据的周长是600米求解即可.
32.
33.
34.
35.或
36.2
37.两组对边分别相等的四边形是平行四边形
38.3或17
解:如图所示:
在矩形中,,则,,
分别是边的中点,
,
,
,
在和中,
,
;
在和中,
,
;
四边形是平行四边形,
,
四边形是矩形,
,
,
;
如图所示:
在矩形中,,则,,
分别是边的中点,
,
,
,
在和中,
,
;
在和中,
,
;
四边形是平行四边形,
,
四边形是矩形,
,
,
,则,
;
综上所述,的长为3或17,
故答案为:3或17.
根据题意分两种情况讨论,进而运用矩形的性质、三角形全等的判定与性质证明四边形是矩形,再结合矩形的性质代入数值,从而即可求解。
39.16
解:∵,分别是边,的中点,且米,
∴BC=2EF=16米,
故答案为:16.
利用三角形中位线的定理及性质求解即可得出答案.
40.
解:过点F作FH⊥AD交AD的延长线于点H,作FM⊥AB于点M,如图所示:
∴四边形AMFH是矩形,
∴FM=AH,AM=FH,
∵AD=4,AE=1,
∴DE=3,
∵四边形ABCD与四边形EFGC是正方形,
∴EF=EC,∠CEF=90°,∠H=∠EDC=90°,
∴∠FEH+∠CED=90°,∠FEH+∠FEH=90°,
∴∠FEH=∠CED,
∴△EFG≌△CED(AAS),
∴FH=DE=3,EH=CD=4,
即点F到AD的距离为3,
∴BM=AB+AM=4+3=7,FM=AE+EH=5,
∴BF=,
故答案为:.
过点F作FH⊥AD交AD的延长线于点H,作FM⊥AB于点M,先利用“AAS”证出△EFG≌△CED,可得FH=DE=3,EH=CD=4,再利用线段的和差求出BM和FM的长,最后利用勾股定理求出BF的长即可.
41.60;75
42.
43.,
44.;
45.
46.
47.;
48.8
49.
50.
期中真题专项复习02 填空题
一、填空题
1.(2024八下·石家庄期中)点关于x轴对称的点的坐标是 .
2.(2024八下·唐山期中)如图,在矩形ABCD中,,以点B为圆心,BC长为半径画弧,交边AD于点E,若AE·ED=,则矩形ABCD的面积为 .
3.(2024八下·承德期中)实验探究:如图所示,对折矩形纸片,使与重合,得到折痕,把纸片展平;再一次折叠纸片,使点落在上,并使折痕经过点,得到折痕,同时得到线段,.请你观察如图,猜想等于 .
4.(2021八下·罗平期中)如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件 (只添一个即可),使四边形ABCD是平行四边形
5.(2019八下·卢龙期中)在函数y= 中,自变量x的取值范围是 .
6.(2024八下·隆化期中)如图,在平面直角坐标系xOy中,直线与x轴交于点A,与y轴交于点B,将△AOB沿过点A的直线折叠,使点B落在x轴负半轴上,记作点C,折痕与y轴交点交于点D,则点C的坐标为 ,点D的坐标为 .
7.(2024八下·丰润期中) 如图, 菱形 ABCD 的边长为. ,对角线AC, BD交于点 O, OA=1, 则菱形ABCD的面积为 .
8.(2024八下·遵化期中)已知一次函数的图象经过点且和直线平行,则该函数的表达式为 .
9.(2024八下·遵化期中)已知点和点关于轴对称,那么 .
10.(2024八下·卢龙期中)某市地铁票价计费标准如表所示:乘车距离x(单位:公里)
乘车距离x
票价(元) 3 4 5 6 每增加1元可乘20公里
另外,使用市政交通一卡通,每个自然月每张卡片支出累计满100元后,超出部分打8折;满150元后,超出部分打5折;支出累计达400元后,不再打折.小红妈妈上班时,需要乘坐地铁15公里到达公司,每天上下班共乘坐两次,如果每次乘坐地铁都使用市政交通一卡通,那么每月第22次乘坐地铁上下班时,她刷卡支出的费用是 元.
11.(2024八下·卢龙期中)点在第-象限,且到y轴的距离为3,直线轴,且.则点C的坐标为 .
12.(2024八下·卢龙期中)点与点关于y轴对称,则的值为 .
13.(2024八下·卢龙期中)剧院里1排5号可以用表示,则表示 .
14.(2024八下·庐江期中)如图所示,平行四边形ABCD中,顶点A、B、D在坐标轴上,AD=5,AB=9,点A的坐标为(﹣3,0),则点C的坐标为
15.(2024八下·平泉期中)如图,菱形的对角线,相交于点,,分别是边,的中点,连接.若,则 (用含的代数式表示);若,,则菱形的面积为
16.(2024八下·宣化期中)平行四边形中,若,则的度数为 .
17.(2024八下·威县期中)如图,在矩形中,,,分别是边的中点,是对角线上的两个动点,且,当四边形中的时,的长为 .
18.(2024八下·宣化期中)某同学参加了马拉松7.5公里健康跑项目,他从起点开始以平均每分钟x公里的速度跑了10分钟,此时他离健康跑终点的路程为y公里,则y与x的函数表达式是 .
19.(2024八下·宣化期中)中国象棋在中国有着三千多年的历史,它难易适中,趣味性强,变化丰富细腻,棋盘棋子文字都体现了中国文化.如图,如果所在位置的坐标为(﹣1,﹣1),所在位置的坐标为(2,﹣1),那么,所在位置的坐标为 .
20.(2024八下·石家庄期中)如图,在中,、相交于点O,,,,的周长为 .
21.(2024八下·澧县期中)如图,在矩形ABCD中,BC=20cm,点P和点Q分别从点B和点D出发,按逆时针方向沿矩形ABCD的边运动,点P和点Q的速度分别为3cm/s和2cm/s,则最快 s后,四边形ABPQ成为矩形.
22.(2024八下·澧县期中)如图,将两条宽度都为3的纸条重叠在一起,使∠ABC=60°,则四边形ABCD的面积为 .
23.(2024八下·定州期中)如图,在中,,为边BC上一动点(且点P不与点B、C重合),于,于.则EF的最小值为 .
24.(2024八下·定州期中)如图,在平面直角坐标系中,四边形是菱形.若点A的坐标是.则菱形的周长为 .
25.(2024八下·定州期中)如图,矩形中,,两条对角线AC、BD所夹的钝角为120°,则BC的长为 .
26.(2024八下·定州期中)如图,在中,D、E分别为AB和AC中点,若,则DE的长为 .
27.(2024八下·盐山期中)如图,E,F分别是的边AB,CD上的点,AF与DE相交于点P,BF与CE相交于点Q.若的面积为2,的面积为4,的面积为26,则阴影部是的面积为 .
28.(2024八下·盐山期中)如图,在矩形ABCD中,对角线AC、BD相交于点O.已知,,则BC的长为 .
29.(2024八下·丰润期中)如图,菱形的边长为,对角线交于点,,则菱形的面积为 .
30.(2024八下·石家庄期中)如图,在平面直角坐标系中,放置一平面镜,其中点的坐标分别为,,从点发射光线,其图象对应的函数解析式为.
①若入射光线与平面镜有公共点,的取值范围是 .
②规定横坐标与纵坐标均为整数的点是整点,光线经过镜面反射后,反射光线与轴相交于点,点是整点的个数是 .
31.(2024八下·石家庄期中)在周长为600米的三角形地块中修建如图所示的三条水渠,则水渠的总长为 米.
32.(2024八下·邯郸经济技术开发期中)在学习《坐标与图形的位置》的课堂上,老师让同学们自主编题,小刚同学编的题目是:“已知正方形ABCD(边长自定),请建立适当的平面直角坐标系,确定正方形ABCD各顶点的坐标”.同桌小华同学按题目要求建立了平面直角坐标系并正确的写出了正方形各顶点的坐标,若在小华同学建立的平面直角坐标系中,正方形ABCD关于x轴对称,但不关于y轴对称,点A的坐标为,则点C的坐标为 .
33.(2024八下·邯郸经济技术开发期中)某水果销售商有100千克苹果,当苹果单价为15元/千克时,能全部销售完,市场调查表明苹果单价每提高1元,销售量减少6千克,若苹果单价提高x元,则苹果销售额y关于x的函数表达式为 .
34.(2024八下·邯郸经济技术开发期中)小明在教室中的座位为第3行第6列,记为,小亮在第5行第1列,记为 .
35.(2024八下·石家庄期中)已知,点P在一次函数的图象上,且到y轴的距离为3,则点P的坐标为 .
36.(2024八下·武邑期中)如图,矩形的对角线的垂直平分线交于点E,交于点F.连接,,若,,则的长为.
37.(2024八下·武邑期中)若在四边形中,的长度之比是,则四边形是平行四边形,判定的依据是.
38.(2024八下·阜平期中) 如图,在矩形中,,,分别是边的中点,是对角线上的两个动点,且,当四边形中的时,的长为 .
39.(2024八下·阜平期中) 如图,某小区要在一块空地上围一个四边形花坛,,分别是边,的中点,且米,则的长为 米.
40.(2024八下·路南期中)四边形ABCD是边长为4的正方形,点E在线段AD上,连接CE,以CE为边,作正方形CEFG(点D,点F在直线CE的同侧),连接BF,如图,当时,则 .
41.(2024八下·任泽期中)如图,在菱形纸片中,.
(1) .
(2)点E在边上,将菱形纸片沿折叠,点C对应点为点,且是的垂直平分线,则的大小为 .
42.(2024八下·大渡口期中)已知点B的坐标为,它向右平移4个单位长度,再向上平移2个单位长度,得到点,则点的坐标为 .
43.(2024八下·安次期中)如图,在平面直角坐标系中,已知点,以点O为圆心,的长为半径画弧,交网格线于点,则①的长为.②a的值是.
44.(2024八下·雄安期中)如图1,E,F分别为矩形纸带的边上的点,,将纸带沿折叠成图2(G为和的交点),则 ;再沿折叠成图3(H为和的交点),则图3中的 .
45.(2024八下·邢台期中)在平面直角坐标系中,已知,点与点关于轴对称,,则的面积为 .
46.(2024八下·邢台期中)某班学生参加学校组织的“垃圾分类”知识竞赛,将学生成绩制成如图所示的频数分布直方图(每组数据包括左端值不包括右端值),其中成绩为“优良”(80分及80分以上)的学生所占百分比为 .
47.(2024八下·献县期中)如图,在菱形中,,,E为边的中点,连接BE,则菱形的面积等于 ,的长等于 .
48.(2024八下·三河期中)如图,在矩形中,,分别是边,上的动点,是线段的中点,,,,为垂足,连接.若,,,则的最小值是 .
49.(2024八下·顺平期中)将形状、大小相同的两个矩形,如图摆放,已知,在边上找一点F,使得,连接.若,则 .
50.(2024八下·昌黎期中)门卫保安老张在校门口观察马路上车辆通行情况,观察了10分钟,其间共有50辆车通过.其中自行车5辆,电动车25辆,汽车20辆,在这段时间内,电动车通过的频率是 .
答案解析部分
1.
2.5
3.
4.BO=DO
∵AO=CO,BO=DO,
∴四边形ABCD是平行四边形.
故答案为:BO=DO.
根据题目条件结合平行四边形的判定方法:对角线互相平分的四边形是平行四边形分别进行分析即可.
5.x≥1
解:根据题意得:x﹣1≥0,
解得:x≥1.
故答案为:x≥1.
因为当函数表达式是二次根式时,被开方数为非负数,所以x﹣1≥0,解不等式可求x的范围.
6.(-1,0);(0,)
7.4
解:∵四边形为菱形,边长为,
∴,,,,
∴,
∴,
∴,
∴菱形的面积为,
故答案为:
先根据菱形的性质得到,,,,进而运用勾股定理求出OB,从而得到BD,再根据菱形的面积公式即可求解。
8.
解:由一次函数y=kx+b的图象平行于直线y=2x﹣3,可知k=2
则一次函数为y=2x+b,
将A的坐标(1,3)代入,得:2+b=3,
解得:b=1
这个一次函数的解析式是y=2x+1.
故答案为:y=2x+1.
本题考查待定系数法求一次函数解析式.根据两直线平行可得k=2,可得直线解析式为y=2x+b,将点A(1,3)代入解析式可求出b的值,据此可求出直线解析式.
9.10
解:点和点关于轴对称,
,,
.
故答案为:10.
本题考查关于轴对称的点的坐标.根据关于轴的对称点的坐标特点:横坐标不变,纵坐标互为相反数.据此可求出的值,据此可求出答案.
10.4
解:小红妈妈每天的上下班的费用分别为5元,即每天10元,10天后花费100元,第22次乘坐地铁时,价格给予8折优惠,此时花费5×0.8=4元,
故答案为:4.
本题考查分段函数的应用问题.根据优惠方案,分别计算每次乘车的费用,再进行累计可求出答案.
11.(3,7)或(3,1)
解:∵点在第一象限,且到轴的距离为,
∴,
∵直线轴,
∴点的横坐标为,
又∵,
∴点的纵坐标为或,
∴点的坐标为或.
故答案为:或.
本题考查坐标与图形的性质.根据点的特征,可求出点的坐标,再根据轴可确定点横坐标,再根据可确定点的纵坐标.分两种情况可写出点的坐标.
12.1
解:∵点与点关于轴对称,
∴,,
解得:,,
∴.
故答案为:.
本题考查关于轴,轴对称的点的坐标特征.根据平面直角坐标系中两点关于轴对称的特征:纵坐标相同,横坐标互为相反,可列出方程组,解方程组可求出,的值,据此可求出式子的值.
13.6排2号
解:∵影院里1排5号可以用表示,
∴表示的是6排2号.
故答案为:6排2号.
本题考查坐标确定位置.根据题意可得,第一个数表示排,第二个数表示号,将有序数对转化为位置问题,可选出答案.
14.(9,4)
解:∵四边形ABCD是平行四边形,
∴CD=AB=9,
∵点A的坐标为(﹣3,0),
∴OA=3,
∴OD==4,
∴点C的坐标为(9,4).
故答案为:(9,4).
由平行四边形的性质得出CD=AB=9,由勾股定理求出OD,即可得出点C的坐标.
15.;
16.60°
17.3或17
18.
19.(﹣3,2)
20.16
21.4
解;设最快x秒,四边形ABPQ成为矩形,由BP=AQ得
3x=20﹣2x.
解得x=4,
故答案为:4.
根据矩形的性质,可得BC与AD的关系,根据矩形的判定定理,可得BP=AQ,根据解题元一次方程,可得答案.
22.6
解:∵纸条的对边平行,即AB∥CD,AD∥BC,
∴四边形ABCD是平行四边形,
∵两张纸条的宽度都是3,
∴S四边形ABCD=AB×3=BC×3,
∴AB=BC,
∴平行四边形ABCD是菱形,即四边形ABCD是菱形.
如图,过A作AE⊥BC,垂足为E,
∵∠ABC=60°,
∴∠BAE=90°﹣60°=30°,
∴AB=2BE,
在△ABE中,AB2=BE2+AE2,
即AB2=AB2+32,
解得AB=2,
∴S四边形ABCD=BC AE=2×3=6.
故答案是:6.
先根据两组对边分别平行证明四边形ABCD是平行四边形,再根据两张纸条的宽度相等,利用面积求出AB=BC,然后根据邻边相等的平行四边形是菱形;根据宽度是3cm与∠ABC=60°求出菱形的边长,然后利用菱形的面积=底×高计算即可.
23.4.8
解:连接
∵,,
∴
∴
∴是直角三角形,
又∵,
∴四边形是矩形
∴
∵当时,有最小值
∴最小
∴
∴
∴
∴
故答案为:.
连接AP,根据勾股定理的逆定理证是直角三角形;根据三个角是直角的四边形是矩形判定四边形AEPF是矩形,得EF=AP;当AP垂直BC时,AP有最小值,故EF最小;根据三角形的面积公式,求出AP,即EF的值.
24.68
解:如图所示,过A作轴于点E,
∵点A的坐标是
∴,
∴
∵四边形是菱形,
∴,
∴菱形的周长.
故答案为:68.
过A作AE⊥x轴于点E,利用勾股定理求出OA的长即可.
25.
解:四边形是矩形,
,,,
,
,
,
是等边三角形,
,
,
,
∴.
故答案为:.
根据矩形的性质证等边三角形AOB,根据等边三角形的性质,结合勾股定理求解.
26.6
解:∵D,E分别是AB,AC的中点,
∴DE是△ABC的中位线,
又BC=12,
∴,
故答案为:6.
三角形的中位线平行于第三边,并且等于第三边的一半,据此求解。
27.7
连接EF,过点E作EM⊥DC于点M,如图所示:
∵S△DEC=DC×EM,S平行四边形ABCD=DC×EM=26,
∴S△DEC=×26=13,
∵四边形ABCD是平行四边形,
∴AB//CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,S△EFQ=S△BCQ,S△EFD=S△ADF,
∴S△EFP=S△ADP,S△APD=2S△APD=2,S△BQC=4,
∴S四边形EPFQ=2+4=6,
∴S阴影=S△DEC-S四边形EPFQ=13-6=7,
故答案为:7.
连接EF,过点E作EM⊥DC于点M,先求出S△EFP=S△ADP,S△APD=2S△APD=2,S△BQC=4,再利用割补法求出S阴影=S△DEC-S四边形EPFQ=13-6=7即可.
28.
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=AC,OB=BD,AC=BD,
∴OA=OD,
∵∠AOB=120°,
∴∠AOD=60°,
∴△AOD是等边三角形,
∴∠ADO=60°,∠BAC=30°,
∴AC=2BC,
∴4BC2=BC2+9,
解得:BC=,
故答案为:.
先证出△AOD是等边三角形,可得∠ADO=60°,∠BAC=30°,再结合4BC2=BC2+9,求出BC的长即可.
29.
30.;7
解:①当入射光线刚好经过点A(4,2)时,
得2=4n+n,
解得:n=;
当入射光线刚好经过点B(4,6)时,
得6=4n+n,
解得:n=,
入射光线与平面镜有公共点,的取值范围是.
故答案为:.
②如图所示,作出点C关于AB的对称点C',作直线AC'、BC'分别交y轴于点E1、E2,
C(-1,0),A(4,2),
C'坐标为(9,0),
设直线AC'的表达式为y1=kx+b(k≠0),
把A(4,2),C'(9,0)代入y1=kx+b(k≠0),
得,
解得:,
直线AC'的表达式为,
设直线BC'的表达式为y2=ax+c(a≠0),
把B(4,6),C'(9,0)代入y2=ax+c(a≠0),
得,
解得:,
直线BC'的表达式为,
当x=0时,,,
即点E1(0,),点E2(0,),
点整点有:4,5,6,7,8,9,10,共7个.
故答案为:7.
①利用待定系数法分别求出直线AC和直线BC的表达式即可得到n的取值范围;
②作出点C关于AB的对称点C',作直线AC'、BC'分别交y轴于点E1、E2,先根据轴对称的性质求出点C'的坐标,再利用待定系数法分别求出AC',BC'的表达式,进而得到AC',BC'于y轴的交点坐标,根据点E的坐标在此范围内即可得到答案.
31.300
解:如图所示,
点D、E、F分别是AB、BC、CD的中点,
DF、DE、EF都是的中位线,
的周长是600米,
BC+AC+AB=600米,
米,
水渠的总长为300米.
故答案为:300.
先证明DF、DE、EF都是的中位线,进而得到再根据的周长是600米求解即可.
32.
33.
34.
35.或
36.2
37.两组对边分别相等的四边形是平行四边形
38.3或17
解:如图所示:
在矩形中,,则,,
分别是边的中点,
,
,
,
在和中,
,
;
在和中,
,
;
四边形是平行四边形,
,
四边形是矩形,
,
,
;
如图所示:
在矩形中,,则,,
分别是边的中点,
,
,
,
在和中,
,
;
在和中,
,
;
四边形是平行四边形,
,
四边形是矩形,
,
,
,则,
;
综上所述,的长为3或17,
故答案为:3或17.
根据题意分两种情况讨论,进而运用矩形的性质、三角形全等的判定与性质证明四边形是矩形,再结合矩形的性质代入数值,从而即可求解。
39.16
解:∵,分别是边,的中点,且米,
∴BC=2EF=16米,
故答案为:16.
利用三角形中位线的定理及性质求解即可得出答案.
40.
解:过点F作FH⊥AD交AD的延长线于点H,作FM⊥AB于点M,如图所示:
∴四边形AMFH是矩形,
∴FM=AH,AM=FH,
∵AD=4,AE=1,
∴DE=3,
∵四边形ABCD与四边形EFGC是正方形,
∴EF=EC,∠CEF=90°,∠H=∠EDC=90°,
∴∠FEH+∠CED=90°,∠FEH+∠FEH=90°,
∴∠FEH=∠CED,
∴△EFG≌△CED(AAS),
∴FH=DE=3,EH=CD=4,
即点F到AD的距离为3,
∴BM=AB+AM=4+3=7,FM=AE+EH=5,
∴BF=,
故答案为:.
过点F作FH⊥AD交AD的延长线于点H,作FM⊥AB于点M,先利用“AAS”证出△EFG≌△CED,可得FH=DE=3,EH=CD=4,再利用线段的和差求出BM和FM的长,最后利用勾股定理求出BF的长即可.
41.60;75
42.
43.,
44.;
45.
46.
47.;
48.8
49.
50.
同课章节目录
