本溪市2009年11月普通高中模块结业验收考试
文档属性
| 名称 | 本溪市2009年11月普通高中模块结业验收考试 |

|
|
| 格式 | zip | ||
| 文件大小 | 228.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-12-19 00:00:00 | ||
图片预览


文档简介
本溪市2009年11月普通高中模块结业验收考试
数学(必修1)试卷
说明:本试卷分第Ⅰ卷和第Ⅱ卷两部分.试卷满分150分,答题时间:120分钟
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12个小题,每小题5分,共60分. 在每小题的四个选项中,只有一项是符合题目要求的.
注意:请在机读答题卡中作答,不要答在试题中
(1)已知集合A{ 1,2,3 },且A中含有一个奇数,则这样的集合A的个数是
(A)1 (B)2 (C)3 (D)4
(2)设全集U是实数集R,M = {或},P = {},则图中阴影部分所表示的集合是
(A){ } (B){}
(C){} (D){}
(3)设表示不超过的最大整数,若函数,则=
(A) (B) (C) (D)
(4)设函数 若,则实数的取值范围是
(A) (B) (C) (D)
(5)已知奇函数R),满足,且,则
(A) (B) (C) (D)2
(6)函数在区间上的值域是,则实数的取值范围是
(A) (B) (C) (D)
(7)函数的零点个数是
(A)0 (B)1 (C)2 (D)3
(8)满足,下列不等式正确的是
(A) (B) (C) (D)
(9)已知函数(且),满足对任意实数,当时,总有,则实数的取值范围是
(A)(1,3) (B)(0,) (C)(1,) (D)(0,1)
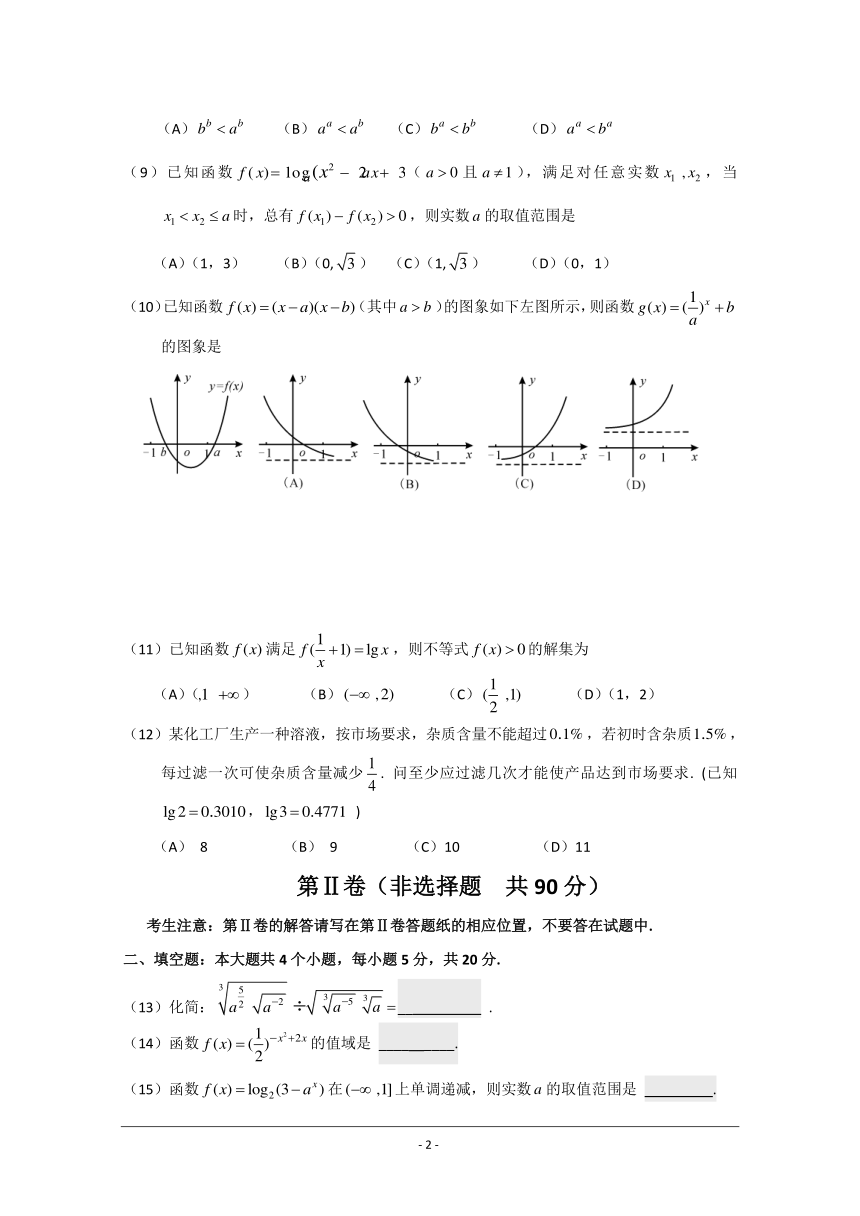
(10)已知函数(其中)的图象如下左图所示,则函数的图象是
(11)已知函数满足,则不等式的解集为
(A)() (B) (C) (D)(1,2)
(12)某化工厂生产一种溶液,按市场要求,杂质含量不能超过,若初时含杂质,每过滤一次可使杂质含量减少. 问至少应过滤几次才能使产品达到市场要求. (已知 , )
(A) 8 (B) 9 (C)10 (D)11
第Ⅱ卷(非选择题 共90分)
考生注意:第Ⅱ卷的解答请写在第Ⅱ卷答题纸的相应位置,不要答在试题中.
二、填空题:本大题共4个小题,每小题5分,共20分.
(13)化简:__ .
(14)函数的值域是 ____ ____.
(15)函数在上单调递减,则实数的取值范围是 .
(16)关于函数(),有下列命题:① 函数图象关于轴对称;
② 当时,函数在上为增函数;③ 当时,函数有最大值,且最大值为;④ 函数的值域是.
其中正确命题的序号是_____________. (写出所有正确命题的序号)
三、解答题:本大题共6个小题,共70分.
(17)(本题满分10分)记函数的定义域为集合A,函数的定义域为集合B.
(Ⅰ)求集合A;
(Ⅱ)若,求实数的取值范围.
(18)(本题满分12分)
(Ⅰ)已知,且,求;
(Ⅱ)解方程:.
(19)(本题满分12分)已知函数.
(Ⅰ)判断并证明的奇偶性;
(Ⅱ)证明在上为减函数.
(20)(本题满分12分)已知二次函数的定义域为R,,在时取得最值. 又若为一次函数,且.
(Ⅰ)求的解析式(含的解析式);
(Ⅱ)若时,恒成立,求实数的取值范围.
(21)(本题满分12分)某化工企业生产甲、乙两种产品.根据市场调查与预测,甲产品的利润与投资成正比,其关系如图(1)所示;乙产品的利润与投资的算术平方根成正比,其关系如图(2)所示.
(Ⅰ)分别将甲、乙两种产品的利润表示为投资的函数关系式;
(Ⅱ)设该企业准备投资100万元资金,并全部投入甲、乙两种产品的生产.怎样分配这100万元资金,才能使企业获得最大利润,其最大利润为多少万元?(精确到1万元)
(22)(本题满分12分)定义在区间D上的函数,如果满足:对任意,存在常数成立,则称是D上的有界函数,其中M称为函数的上界.已知函数
(Ⅰ)当时,求函数在(,0)上的值域,并判断在(,0)上是否为有界函数,请说明理由;
(Ⅱ)若函数在上是以3为上界的有界函数,求实数的取值范围.
本溪市2009年11月普通高中模块结业验收考试
数学(必修1)试卷参考答案
一、选择题:1.D 2.B 3.B 4.A 5.D 6.B 7.C 8.D 9.C 10.A 11.D 12.C
二、填空题:13. (或或) 14. 15. 16. ①③
三、解答题:
17.解:(Ⅰ)由已知得: A={ …… 4分
(Ⅱ)由B={={ …… 6分
B={或 …… 8分
AB ……10分
18.解:(Ⅰ) 由 得 …… 2分
=2 …… 4分
又 …… 6分
(Ⅱ)方程 ,可化为
两边同乘以并整理得: …… 8分
或 …… 10分
或 ……12分19. 解:(Ⅰ)为奇函数. …… 2分
证明如下:函数的定义域为R,
且 …… 4分
为奇函数 …… 6分
(Ⅱ)设R,则,设
则,
()()=
…… 8分,…10分
函数在上为减函数 ……12分
20. 解:(Ⅰ)设 …… 2分
又 ,为一次函数
…………4分
的解析式为 ……5分
(Ⅱ)由(Ⅰ)可知,
当时,要使,恒成立, 则有,
即,此时符合条件的不存在; ……7分
当时 ,要使,恒成立, 则有
即此时符合条件的的范围是 ……9分
当时,要使,恒成立, 则有
即 显然成立,此时符合条件的的范围是 ……… 11分
综合上述可知,实数的取值范围是 …… 12分
21. 解:(Ⅰ)设投资为万元,甲产品的利润为万元,乙产品的利润为万元
由题设 …… 2分
由图(1)可知,由图(2)可知, … 4分
…… 6分
(Ⅱ) 设甲产品投入万元,则乙产品投入为100万元,设企业利润为万元
则 () …… 8分
设,则
()
时,,此时 …… 10分
当甲产品投入万元,则乙产品投入为20.25万元时,企业获得的最大利润为30万元. …… 12分
22. 解:(Ⅰ)当时,在(,0)上单调递减, ……2分
所以,即在(,0)上的值域为(3, ……4分
故不存在常数成立,
所以在(,0)上不是有界函数 ……6分
(Ⅱ)由题意可知,在上恒成立,即
即,
即 在上恒成立,
……8分
设, ,由,
设,,
在上递减,在上递增 ……10分
在的最大值为,在上的最小值为1
实数的取值范围是[,1]. ……12分
PAGE
- 1 -
数学(必修1)试卷
说明:本试卷分第Ⅰ卷和第Ⅱ卷两部分.试卷满分150分,答题时间:120分钟
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12个小题,每小题5分,共60分. 在每小题的四个选项中,只有一项是符合题目要求的.
注意:请在机读答题卡中作答,不要答在试题中
(1)已知集合A{ 1,2,3 },且A中含有一个奇数,则这样的集合A的个数是
(A)1 (B)2 (C)3 (D)4
(2)设全集U是实数集R,M = {或},P = {},则图中阴影部分所表示的集合是
(A){ } (B){}
(C){} (D){}
(3)设表示不超过的最大整数,若函数,则=
(A) (B) (C) (D)
(4)设函数 若,则实数的取值范围是
(A) (B) (C) (D)
(5)已知奇函数R),满足,且,则
(A) (B) (C) (D)2
(6)函数在区间上的值域是,则实数的取值范围是
(A) (B) (C) (D)
(7)函数的零点个数是
(A)0 (B)1 (C)2 (D)3
(8)满足,下列不等式正确的是
(A) (B) (C) (D)
(9)已知函数(且),满足对任意实数,当时,总有,则实数的取值范围是
(A)(1,3) (B)(0,) (C)(1,) (D)(0,1)
(10)已知函数(其中)的图象如下左图所示,则函数的图象是
(11)已知函数满足,则不等式的解集为
(A)() (B) (C) (D)(1,2)
(12)某化工厂生产一种溶液,按市场要求,杂质含量不能超过,若初时含杂质,每过滤一次可使杂质含量减少. 问至少应过滤几次才能使产品达到市场要求. (已知 , )
(A) 8 (B) 9 (C)10 (D)11
第Ⅱ卷(非选择题 共90分)
考生注意:第Ⅱ卷的解答请写在第Ⅱ卷答题纸的相应位置,不要答在试题中.
二、填空题:本大题共4个小题,每小题5分,共20分.
(13)化简:__ .
(14)函数的值域是 ____ ____.
(15)函数在上单调递减,则实数的取值范围是 .
(16)关于函数(),有下列命题:① 函数图象关于轴对称;
② 当时,函数在上为增函数;③ 当时,函数有最大值,且最大值为;④ 函数的值域是.
其中正确命题的序号是_____________. (写出所有正确命题的序号)
三、解答题:本大题共6个小题,共70分.
(17)(本题满分10分)记函数的定义域为集合A,函数的定义域为集合B.
(Ⅰ)求集合A;
(Ⅱ)若,求实数的取值范围.
(18)(本题满分12分)
(Ⅰ)已知,且,求;
(Ⅱ)解方程:.
(19)(本题满分12分)已知函数.
(Ⅰ)判断并证明的奇偶性;
(Ⅱ)证明在上为减函数.
(20)(本题满分12分)已知二次函数的定义域为R,,在时取得最值. 又若为一次函数,且.
(Ⅰ)求的解析式(含的解析式);
(Ⅱ)若时,恒成立,求实数的取值范围.
(21)(本题满分12分)某化工企业生产甲、乙两种产品.根据市场调查与预测,甲产品的利润与投资成正比,其关系如图(1)所示;乙产品的利润与投资的算术平方根成正比,其关系如图(2)所示.
(Ⅰ)分别将甲、乙两种产品的利润表示为投资的函数关系式;
(Ⅱ)设该企业准备投资100万元资金,并全部投入甲、乙两种产品的生产.怎样分配这100万元资金,才能使企业获得最大利润,其最大利润为多少万元?(精确到1万元)
(22)(本题满分12分)定义在区间D上的函数,如果满足:对任意,存在常数成立,则称是D上的有界函数,其中M称为函数的上界.已知函数
(Ⅰ)当时,求函数在(,0)上的值域,并判断在(,0)上是否为有界函数,请说明理由;
(Ⅱ)若函数在上是以3为上界的有界函数,求实数的取值范围.
本溪市2009年11月普通高中模块结业验收考试
数学(必修1)试卷参考答案
一、选择题:1.D 2.B 3.B 4.A 5.D 6.B 7.C 8.D 9.C 10.A 11.D 12.C
二、填空题:13. (或或) 14. 15. 16. ①③
三、解答题:
17.解:(Ⅰ)由已知得: A={ …… 4分
(Ⅱ)由B={={ …… 6分
B={或 …… 8分
AB ……10分
18.解:(Ⅰ) 由 得 …… 2分
=2 …… 4分
又 …… 6分
(Ⅱ)方程 ,可化为
两边同乘以并整理得: …… 8分
或 …… 10分
或 ……12分19. 解:(Ⅰ)为奇函数. …… 2分
证明如下:函数的定义域为R,
且 …… 4分
为奇函数 …… 6分
(Ⅱ)设R,则,设
则,
()()=
…… 8分,…10分
函数在上为减函数 ……12分
20. 解:(Ⅰ)设 …… 2分
又 ,为一次函数
…………4分
的解析式为 ……5分
(Ⅱ)由(Ⅰ)可知,
当时,要使,恒成立, 则有,
即,此时符合条件的不存在; ……7分
当时 ,要使,恒成立, 则有
即此时符合条件的的范围是 ……9分
当时,要使,恒成立, 则有
即 显然成立,此时符合条件的的范围是 ……… 11分
综合上述可知,实数的取值范围是 …… 12分
21. 解:(Ⅰ)设投资为万元,甲产品的利润为万元,乙产品的利润为万元
由题设 …… 2分
由图(1)可知,由图(2)可知, … 4分
…… 6分
(Ⅱ) 设甲产品投入万元,则乙产品投入为100万元,设企业利润为万元
则 () …… 8分
设,则
()
时,,此时 …… 10分
当甲产品投入万元,则乙产品投入为20.25万元时,企业获得的最大利润为30万元. …… 12分
22. 解:(Ⅰ)当时,在(,0)上单调递减, ……2分
所以,即在(,0)上的值域为(3, ……4分
故不存在常数成立,
所以在(,0)上不是有界函数 ……6分
(Ⅱ)由题意可知,在上恒成立,即
即,
即 在上恒成立,
……8分
设, ,由,
设,,
在上递减,在上递增 ……10分
在的最大值为,在上的最小值为1
实数的取值范围是[,1]. ……12分
PAGE
- 1 -
同课章节目录
