《第12讲:组合图形的面积》小升初人教版六年级数学专题复习(学案)
文档属性
| 名称 | 《第12讲:组合图形的面积》小升初人教版六年级数学专题复习(学案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 17:51:01 | ||
图片预览


文档简介
小升初人教版六年级数学专题复习
第12讲:组合图形的面积
【经典案例】
【例1】如图,已知正方形的边长是6cm,求图中阴影部分的面积。
【思路提示】
求复杂图形的面积可以用割补等方法,将复杂图形转化为学过的图形。
【思路分析】
如图,在图中画两条虚线,发现:
①原图中圆内空白部分的面积=圆外空白部分的面积;
②正方形的面积一一个整圆的面积=图中空白部分面积的一半;
③正方形的面积一全部空白部分的面积=阴影部分的面积。
【规范解答】
6×6-(6÷2) ×3.14=7.74(cm )
6×6-7.74×2=20.52(cm )
答:阴影部分的面积是20.52cm 。
【方法点拨】
根据图形的特点,对图形进行分割,将一个图形的面积转化为两个图形的面积和(差),使隐蔽的关系明朗化,从而顺利解题。
【强化训练】
【原型题】
原型题1:求下面图中阴影部分的面积。 订正:
原型题2:如图,半圆中长方形的宽是长的一半,圆的半径为4cm,则阴影部分的面积是多少平方厘米 订正:
【变式题】
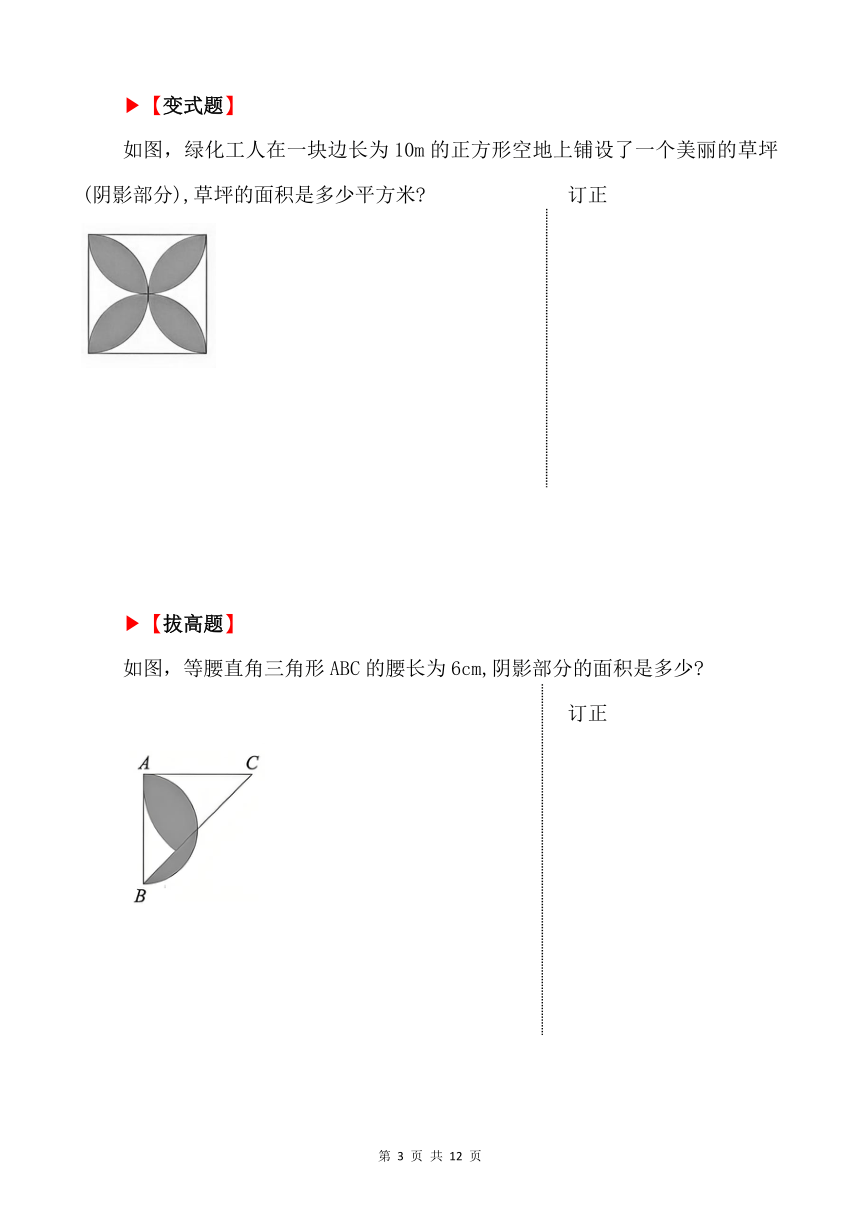
如图,绿化工人在一块边长为10m的正方形空地上铺设了一个美丽的草坪(阴影部分),草坪的面积是多少平方米 订正
【拔高题】
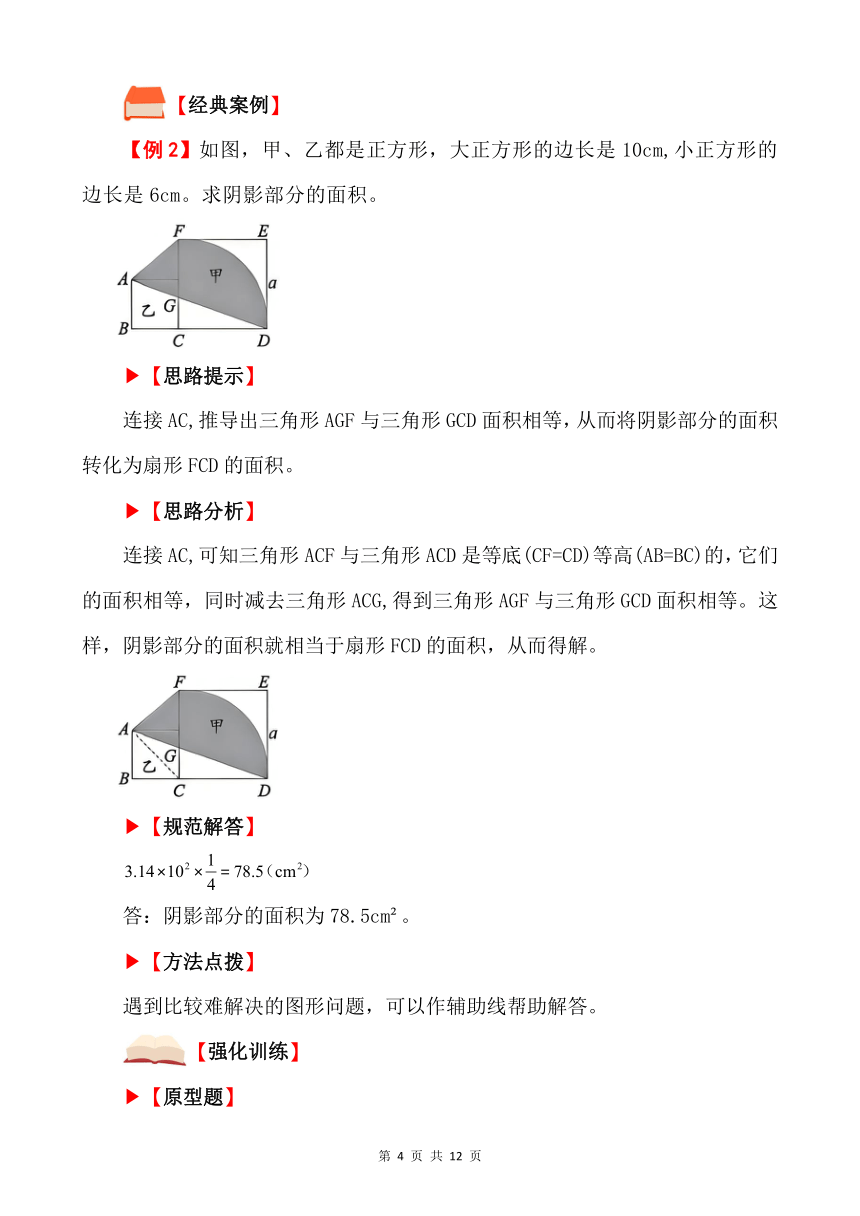
如图,等腰直角三角形ABC的腰长为6cm,阴影部分的面积是多少 订正
【经典案例】
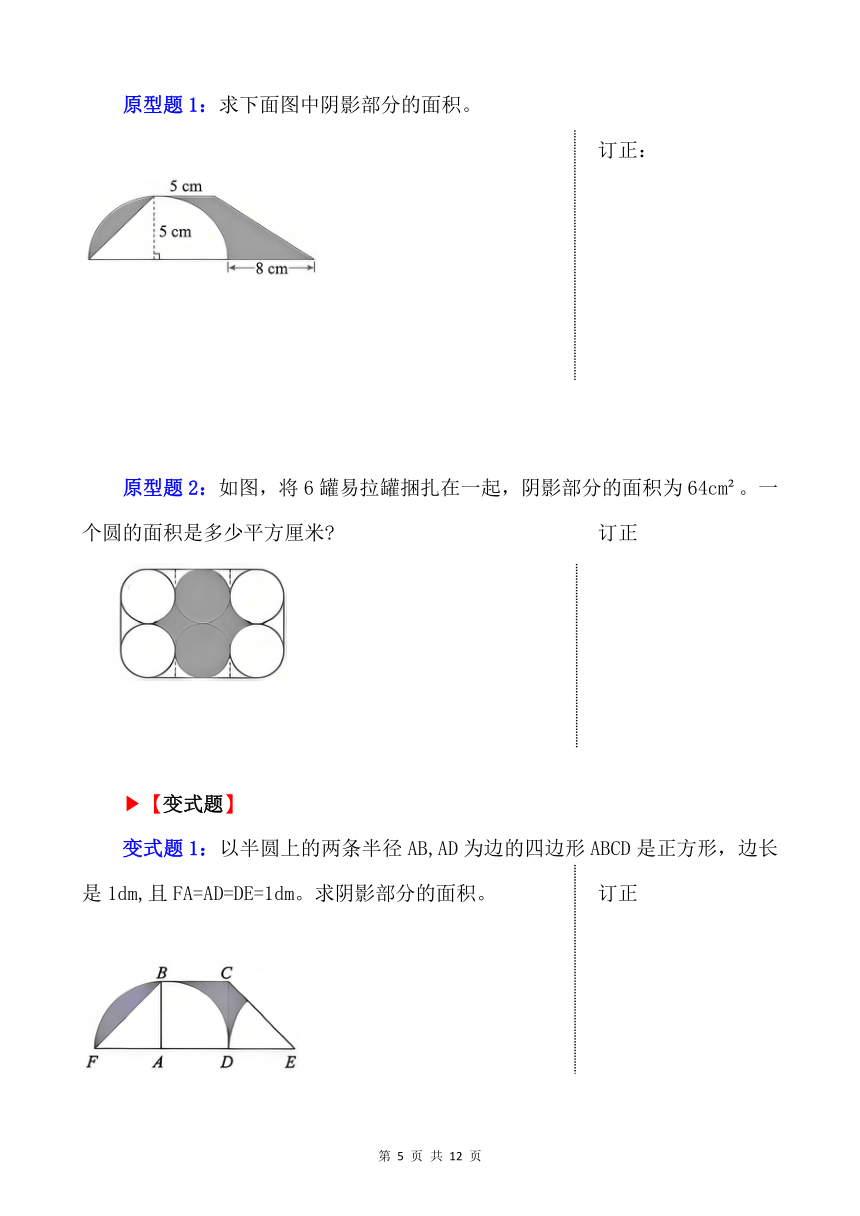
【例2】如图,甲、乙都是正方形,大正方形的边长是10cm,小正方形的边长是6cm。求阴影部分的面积。
【思路提示】
连接AC,推导出三角形AGF与三角形GCD面积相等,从而将阴影部分的面积转化为扇形FCD的面积。
【思路分析】
连接AC,可知三角形ACF与三角形ACD是等底(CF=CD)等高(AB=BC)的,它们的面积相等,同时减去三角形ACG,得到三角形AGF与三角形GCD面积相等。这样,阴影部分的面积就相当于扇形FCD的面积,从而得解。
【规范解答】
答:阴影部分的面积为78.5cm 。
【方法点拨】
遇到比较难解决的图形问题,可以作辅助线帮助解答。
【强化训练】
【原型题】
原型题1:求下面图中阴影部分的面积。
订正:
原型题2:如图,将6罐易拉罐捆扎在一起,阴影部分的面积为64cm 。一个圆的面积是多少平方厘米 订正
【变式题】
变式题1:以半圆上的两条半径AB,AD为边的四边形ABCD是正方形,边长是1dm,且FA=AD=DE=1dm。求阴影部分的面积。 订正
变式题2:如图,平行四边形ABCD的面积是100cm 。求阴影部分的面积。 订正
【拔高题】
如图,BO=2DO,阴影部分的面积是4cm 。那么,梯形ABCD的面积是多少平方厘米 订正
【经典案例】
【例3】求图中阴影部分的面积。(单位:cm)
【思路提示】
运用割补法将阴影部分的面积转化为大圆的面积—三角形AOB的面积去计算。
【思路分析】
观察上图,图中阴影部分的面积不规则,可以将左下角的阴影部分分为两部分,将这两部分分别补在阴影部分的位置,使图形得到转化,如下图所示:
由上图可知,阴影部分的面积等于扇形AOB与三角形AOB的面积之差,所以阴影部分的面积=大圆的面积-三角形AOB的面积。
【规范解答】
答:阴影部分的面积是4.56cm 。
【方法点拨】
将不规则图形的面积利用分割移补法,转化为一个面积大小不变的规则的图形去计算,更为简单。
【强化训练】
【原型题】
原型题1:求图中阴影部分的面积。(单位:cm)
订正:
原型题2:图中四个圆的半径都是3cm,求阴影部分的面积。
订正
【变式题】
变式题1:在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(如图),求图中阴影部分的面积占整个图形面积的几分之几。 订正
变式题2:右图是一个漂亮的图形,图中大圆的直径是6cm,阴影部分的面积为多少平方厘米 订正
【拔高题】
如图,把长方形ABCD绕点A顺时针旋转90°,求阴影部分的面积。(单位:cm) 订正
参考答案
【例1】 【原型题1】
6×6÷2=18(m2)
【例1】 【原型题1】
3.14×4 ÷2-4×4÷2×2=9.12(cm )
【例1】 【变式题】
2×3.14×(10÷2) -10 =57(m )
【例1】 【拔高题】
【例2】 【原型题1】
(5+8)×5÷2=32.5(cm )
提示:如图,用割补法可看出阴影部分是一个上底为5cm,下底为8cm,高为5cm的梯形。
【例2】 【原型题2】
圆的半径的平方:64÷8=8
一个圆的面积:3.14×8=25.12(cm )
【例2】 【变式题1】
解析:连接BD,如图所示:
【例2】 【变式题2】
连接AC(图略),可以看出平行四边形ABCD面积的一半等于圆半径的平方。阴影部分的面积:
【例2】 【拔高题】
答案:18cm
解析:根据三角形等底等高面积相等的性质。
三角形BCD的面积=三角形ACD的面积,所以三角形BOC的面积=三角形AOD的面积=4cm 。因为BO=2DO,所以三角形COD的面积=三角形BOC的面积÷2=2 cm 。因为三角形AOB的面积=三角形AOD的面积×2=8cm ,所以梯形ABCD的面积为8+4+4+2=18(cm )。
【例3】 【原型题1】
【例3】 【原型题2】
3.14×3 ×2+(3+3)×(3+3)=92.52(cm )
解析:将图形进行割补,如下图:把阴影部分分割补成四个半圆和一个正方形,四个半圆可以看成是两个圆,求两个圆的面积:3.14×3 ×2=56.52(cm ),再求出正方形的面积:(3+3)×(3+3)=36(cm ),最后两个面积相加得出阴影部分的面积。
【例3】 【变式题1】
如下图所示,将等腰三角形分成两个直角三角形,再拼成一个长方形,阴影部分的面积正好是长方形的三分之一,所以阴影部分占整个图形面积的三分之一。
【例3】 【变式题2】
6÷2=3(cm)
3.14×3 -3×3-3.14×(3÷2) ×2=5.13(cm )
【例3】 【拔高题】
3.14×10 ÷4-3.14×8 ÷4=28.26(cm )
第12讲:组合图形的面积
【经典案例】
【例1】如图,已知正方形的边长是6cm,求图中阴影部分的面积。
【思路提示】
求复杂图形的面积可以用割补等方法,将复杂图形转化为学过的图形。
【思路分析】
如图,在图中画两条虚线,发现:
①原图中圆内空白部分的面积=圆外空白部分的面积;
②正方形的面积一一个整圆的面积=图中空白部分面积的一半;
③正方形的面积一全部空白部分的面积=阴影部分的面积。
【规范解答】
6×6-(6÷2) ×3.14=7.74(cm )
6×6-7.74×2=20.52(cm )
答:阴影部分的面积是20.52cm 。
【方法点拨】
根据图形的特点,对图形进行分割,将一个图形的面积转化为两个图形的面积和(差),使隐蔽的关系明朗化,从而顺利解题。
【强化训练】
【原型题】
原型题1:求下面图中阴影部分的面积。 订正:
原型题2:如图,半圆中长方形的宽是长的一半,圆的半径为4cm,则阴影部分的面积是多少平方厘米 订正:
【变式题】
如图,绿化工人在一块边长为10m的正方形空地上铺设了一个美丽的草坪(阴影部分),草坪的面积是多少平方米 订正
【拔高题】
如图,等腰直角三角形ABC的腰长为6cm,阴影部分的面积是多少 订正
【经典案例】
【例2】如图,甲、乙都是正方形,大正方形的边长是10cm,小正方形的边长是6cm。求阴影部分的面积。
【思路提示】
连接AC,推导出三角形AGF与三角形GCD面积相等,从而将阴影部分的面积转化为扇形FCD的面积。
【思路分析】
连接AC,可知三角形ACF与三角形ACD是等底(CF=CD)等高(AB=BC)的,它们的面积相等,同时减去三角形ACG,得到三角形AGF与三角形GCD面积相等。这样,阴影部分的面积就相当于扇形FCD的面积,从而得解。
【规范解答】
答:阴影部分的面积为78.5cm 。
【方法点拨】
遇到比较难解决的图形问题,可以作辅助线帮助解答。
【强化训练】
【原型题】
原型题1:求下面图中阴影部分的面积。
订正:
原型题2:如图,将6罐易拉罐捆扎在一起,阴影部分的面积为64cm 。一个圆的面积是多少平方厘米 订正
【变式题】
变式题1:以半圆上的两条半径AB,AD为边的四边形ABCD是正方形,边长是1dm,且FA=AD=DE=1dm。求阴影部分的面积。 订正
变式题2:如图,平行四边形ABCD的面积是100cm 。求阴影部分的面积。 订正
【拔高题】
如图,BO=2DO,阴影部分的面积是4cm 。那么,梯形ABCD的面积是多少平方厘米 订正
【经典案例】
【例3】求图中阴影部分的面积。(单位:cm)
【思路提示】
运用割补法将阴影部分的面积转化为大圆的面积—三角形AOB的面积去计算。
【思路分析】
观察上图,图中阴影部分的面积不规则,可以将左下角的阴影部分分为两部分,将这两部分分别补在阴影部分的位置,使图形得到转化,如下图所示:
由上图可知,阴影部分的面积等于扇形AOB与三角形AOB的面积之差,所以阴影部分的面积=大圆的面积-三角形AOB的面积。
【规范解答】
答:阴影部分的面积是4.56cm 。
【方法点拨】
将不规则图形的面积利用分割移补法,转化为一个面积大小不变的规则的图形去计算,更为简单。
【强化训练】
【原型题】
原型题1:求图中阴影部分的面积。(单位:cm)
订正:
原型题2:图中四个圆的半径都是3cm,求阴影部分的面积。
订正
【变式题】
变式题1:在一个等腰三角形中,两条与底边平行的线段将三角形的两条边等分成三段(如图),求图中阴影部分的面积占整个图形面积的几分之几。 订正
变式题2:右图是一个漂亮的图形,图中大圆的直径是6cm,阴影部分的面积为多少平方厘米 订正
【拔高题】
如图,把长方形ABCD绕点A顺时针旋转90°,求阴影部分的面积。(单位:cm) 订正
参考答案
【例1】 【原型题1】
6×6÷2=18(m2)
【例1】 【原型题1】
3.14×4 ÷2-4×4÷2×2=9.12(cm )
【例1】 【变式题】
2×3.14×(10÷2) -10 =57(m )
【例1】 【拔高题】
【例2】 【原型题1】
(5+8)×5÷2=32.5(cm )
提示:如图,用割补法可看出阴影部分是一个上底为5cm,下底为8cm,高为5cm的梯形。
【例2】 【原型题2】
圆的半径的平方:64÷8=8
一个圆的面积:3.14×8=25.12(cm )
【例2】 【变式题1】
解析:连接BD,如图所示:
【例2】 【变式题2】
连接AC(图略),可以看出平行四边形ABCD面积的一半等于圆半径的平方。阴影部分的面积:
【例2】 【拔高题】
答案:18cm
解析:根据三角形等底等高面积相等的性质。
三角形BCD的面积=三角形ACD的面积,所以三角形BOC的面积=三角形AOD的面积=4cm 。因为BO=2DO,所以三角形COD的面积=三角形BOC的面积÷2=2 cm 。因为三角形AOB的面积=三角形AOD的面积×2=8cm ,所以梯形ABCD的面积为8+4+4+2=18(cm )。
【例3】 【原型题1】
【例3】 【原型题2】
3.14×3 ×2+(3+3)×(3+3)=92.52(cm )
解析:将图形进行割补,如下图:把阴影部分分割补成四个半圆和一个正方形,四个半圆可以看成是两个圆,求两个圆的面积:3.14×3 ×2=56.52(cm ),再求出正方形的面积:(3+3)×(3+3)=36(cm ),最后两个面积相加得出阴影部分的面积。
【例3】 【变式题1】
如下图所示,将等腰三角形分成两个直角三角形,再拼成一个长方形,阴影部分的面积正好是长方形的三分之一,所以阴影部分占整个图形面积的三分之一。
【例3】 【变式题2】
6÷2=3(cm)
3.14×3 -3×3-3.14×(3÷2) ×2=5.13(cm )
【例3】 【拔高题】
3.14×10 ÷4-3.14×8 ÷4=28.26(cm )
同课章节目录
