《第13讲:圆的周长》小升初人教版六年级数学专题复习(学案)
文档属性
| 名称 | 《第13讲:圆的周长》小升初人教版六年级数学专题复习(学案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 17:52:28 | ||
图片预览


文档简介
小升初人教版六年级数学专题复习
第13讲:圆的周长
【经典案例】
【例1】一只小蚂蚁要从A到C(如图),它有两条不同的路线可以走,哪条路线比较短
【思路提示】
观察发现:大半圆的直径AC,等于两个小半圆的直径AB、BC的和。计算半圆的周长时,要注意明确是否包括直径。
【思路分析】
要想知道哪条路线比较短,就要分别计算出路线①和路线②的长度,再进行比较。
仔细观察可知,路线①是直径为AC的圆的周长的一半,路线②是直径分别为AB,BC的圆的周长的一半的和。
【规范解答】
路线①:3.14×(80+40)÷2=188.4(cm)
路线②:3.14×80÷2+3.14×40÷2=188.4(cm)
188.4=188.4
答:两条路线同样长。
【方法点拨】
由几个半圆围成的图形,若大半圆的直径等于几个小半 圆的直径和,则大半圆的周长等于这几个小半圆的周长和。
【强化训练】
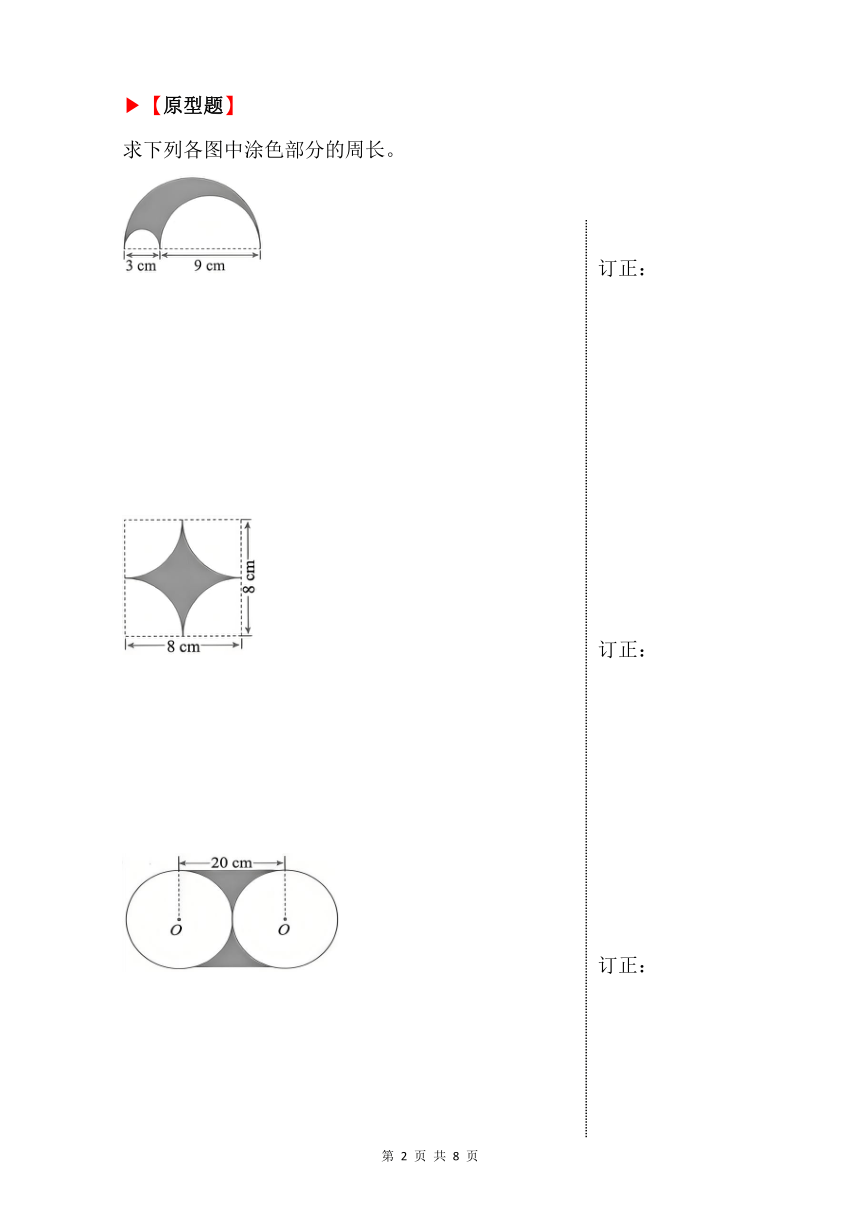
【原型题】
求下列各图中涂色部分的周长。
订正:
订正:
订正:
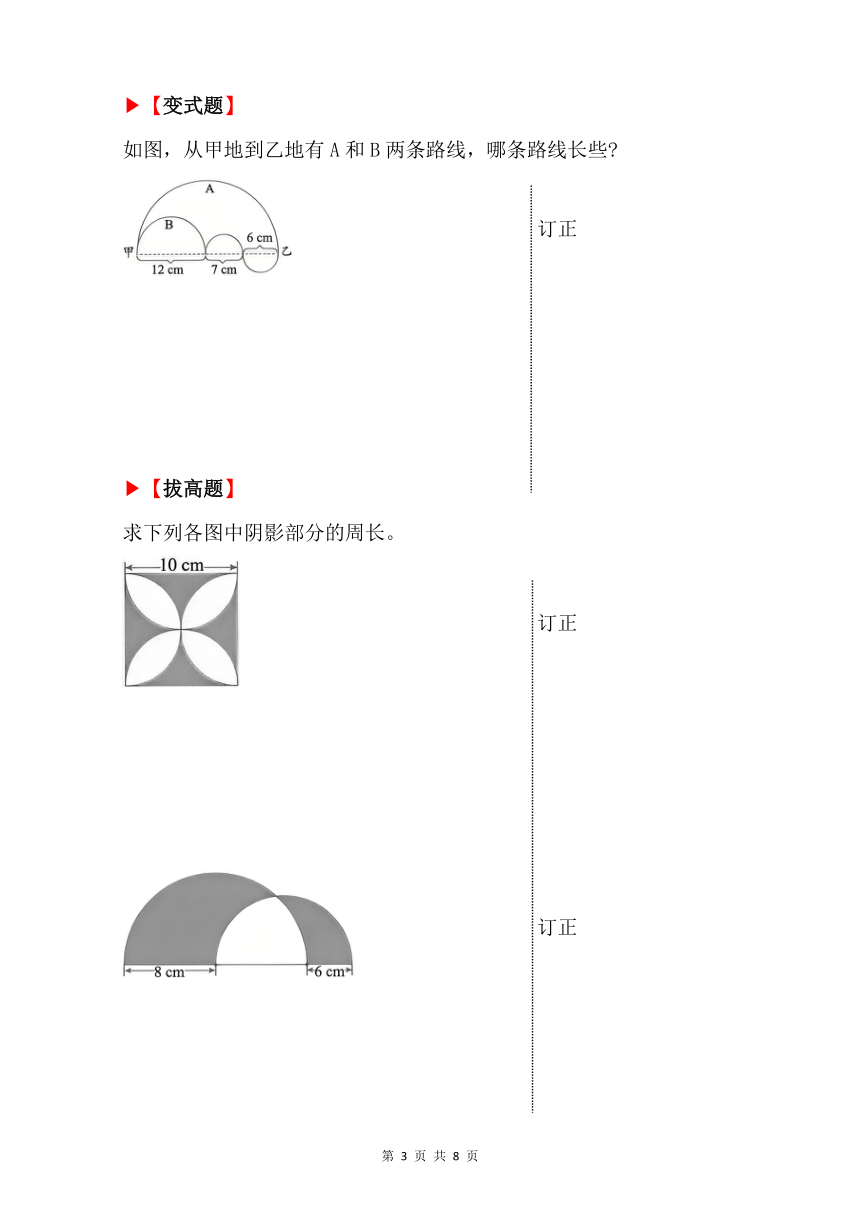
【变式题】
如图,从甲地到乙地有A和B两条路线,哪条路线长些
订正
【拔高题】
求下列各图中阴影部分的周长。
订正
订正
【经典案例】
【例2】王叔叔到商店买了4瓶一样的啤酒,售货员将4瓶啤酒捆扎在一起,如图所示,捆3圈至少用绳子多少厘米 (一个啤酒瓶底面圆的直径为7cm)
【思路提示】
可以将绳子的长度分为曲线部分和线段部分分别计算。
【思路分析】
观察发现,绳子的长度包含两部分:第一部分是环绕在啤酒瓶上的曲线部分的绳长,第二部分是两个啤酒瓶之间的线段部分的绳长。如下图所示:
【规范解答】
3.14×7+7×4=49.98(cm) 49.98×3=149.94(cm)
【方法点拨】
计算复杂图形的周长,关键是确定由哪几条线段或圆弧组成,通过分解组成,曲、直分开计算,线段与线段相加,圆弧与圆弧组合,最后求总长。
【强化训练】
【原型题】
原型题1:如图有3根截面直径都是4dm的圆柱形木棍,用一根绳子把它们捆成一捆(接头处不计),最短需要多少分米的绳子 订正:
原型题2:把底面直径为6dm的圆柱形钢管用铁丝捆成如图所示的形状(从底部看),若接头处不计,至少需要多少分米长的铁丝 订正:
【变式题】
变式题1:有7根直径为10cm的塑料管(厚度忽略不计),如图所示,用一根绳子把它们捆在一起,如果接头处忽略不计,绳子的长度至少是多少厘米 订正
变式题2:下面是一个花瓣图形,它是由8个直径是2cm的小圆的圆周的一部分连成的,图中蓝点是这些圆的圆心。花瓣图形的周长和面积分别是多少 订正
【拔高题】
把一些同样大小的圆柱形木头分别捆成如下图所示(从底面方向看)的形状,图中每个圆的直径都是20cm。像这样继续捆下去,第④组至少需要多少厘米的绳子 第n组呢 订正
参考答案
【例1】 【原型题】
图1:3.14×3÷2=4.71(cm) 3.14×9÷2=14.13(cm)
3.14×(3+9)÷2=18.84(cm) 4.71+14.13+18.84=37.68(cm)
图2:3.14×8=25.12(cm)
图3:3.14×20+20×2=102.8(cm)
【例1】 【变式题】
3.14×(12+7+6)÷2=39.25(cm)
3.14×12÷2+3.14×7÷2+3.14×6÷2=39.25(cm)
39.25=39.25
A和B两条路线一样长。
【例1】 【拔高题】
图1:3.14×10×2+10×4=102.8(cm)
图2:3.14×8+3.14×(8+6)÷2+8+6=61.1(cm)
解析:如图,可知阴影部分的周长由四部分组成。
阴影部分的周长=圆O 周长的一半十圆O 周长的一半十线段AO 的长度十线段BC的长度。
【例2】 【原型题1】
3.14×4+3×4=24.56(dm)
【例2】 【原型题2】
3.14×6+6×5=48.84(dm)
【例2】 【变式题1】
3.14×10+6×10=91.4(cm)
【例2】 【变式题2】
周长:5×3.14×2=31.4(cm)
面积:4×4+3.14×1 =19.14(cm )
解析:作辅助线:
从图中可以看出:花瓣图形的周长等于4个半径为1cm的圆周长的一半加上4个半径为1cm的圆周长白的,即等于5个半径为1cm的圆的周长。花瓣图形的面积等于边长为4cm的正方形的面积加上1个半径为1cm的圆的面积。
【例2】 【拔高题】
3.14×20+20×4×4=382.8(cm)
3.14×20+20n×4=(62.8+80n)cm
解析:每一行两边都是1,每一个数等于它上方两数之和。第7行数字为1,6,15,20,15,6,1,第8行数字为1,7,21,35,35,21,7,1,所以第5个数是35。
第13讲:圆的周长
【经典案例】
【例1】一只小蚂蚁要从A到C(如图),它有两条不同的路线可以走,哪条路线比较短
【思路提示】
观察发现:大半圆的直径AC,等于两个小半圆的直径AB、BC的和。计算半圆的周长时,要注意明确是否包括直径。
【思路分析】
要想知道哪条路线比较短,就要分别计算出路线①和路线②的长度,再进行比较。
仔细观察可知,路线①是直径为AC的圆的周长的一半,路线②是直径分别为AB,BC的圆的周长的一半的和。
【规范解答】
路线①:3.14×(80+40)÷2=188.4(cm)
路线②:3.14×80÷2+3.14×40÷2=188.4(cm)
188.4=188.4
答:两条路线同样长。
【方法点拨】
由几个半圆围成的图形,若大半圆的直径等于几个小半 圆的直径和,则大半圆的周长等于这几个小半圆的周长和。
【强化训练】
【原型题】
求下列各图中涂色部分的周长。
订正:
订正:
订正:
【变式题】
如图,从甲地到乙地有A和B两条路线,哪条路线长些
订正
【拔高题】
求下列各图中阴影部分的周长。
订正
订正
【经典案例】
【例2】王叔叔到商店买了4瓶一样的啤酒,售货员将4瓶啤酒捆扎在一起,如图所示,捆3圈至少用绳子多少厘米 (一个啤酒瓶底面圆的直径为7cm)
【思路提示】
可以将绳子的长度分为曲线部分和线段部分分别计算。
【思路分析】
观察发现,绳子的长度包含两部分:第一部分是环绕在啤酒瓶上的曲线部分的绳长,第二部分是两个啤酒瓶之间的线段部分的绳长。如下图所示:
【规范解答】
3.14×7+7×4=49.98(cm) 49.98×3=149.94(cm)
【方法点拨】
计算复杂图形的周长,关键是确定由哪几条线段或圆弧组成,通过分解组成,曲、直分开计算,线段与线段相加,圆弧与圆弧组合,最后求总长。
【强化训练】
【原型题】
原型题1:如图有3根截面直径都是4dm的圆柱形木棍,用一根绳子把它们捆成一捆(接头处不计),最短需要多少分米的绳子 订正:
原型题2:把底面直径为6dm的圆柱形钢管用铁丝捆成如图所示的形状(从底部看),若接头处不计,至少需要多少分米长的铁丝 订正:
【变式题】
变式题1:有7根直径为10cm的塑料管(厚度忽略不计),如图所示,用一根绳子把它们捆在一起,如果接头处忽略不计,绳子的长度至少是多少厘米 订正
变式题2:下面是一个花瓣图形,它是由8个直径是2cm的小圆的圆周的一部分连成的,图中蓝点是这些圆的圆心。花瓣图形的周长和面积分别是多少 订正
【拔高题】
把一些同样大小的圆柱形木头分别捆成如下图所示(从底面方向看)的形状,图中每个圆的直径都是20cm。像这样继续捆下去,第④组至少需要多少厘米的绳子 第n组呢 订正
参考答案
【例1】 【原型题】
图1:3.14×3÷2=4.71(cm) 3.14×9÷2=14.13(cm)
3.14×(3+9)÷2=18.84(cm) 4.71+14.13+18.84=37.68(cm)
图2:3.14×8=25.12(cm)
图3:3.14×20+20×2=102.8(cm)
【例1】 【变式题】
3.14×(12+7+6)÷2=39.25(cm)
3.14×12÷2+3.14×7÷2+3.14×6÷2=39.25(cm)
39.25=39.25
A和B两条路线一样长。
【例1】 【拔高题】
图1:3.14×10×2+10×4=102.8(cm)
图2:3.14×8+3.14×(8+6)÷2+8+6=61.1(cm)
解析:如图,可知阴影部分的周长由四部分组成。
阴影部分的周长=圆O 周长的一半十圆O 周长的一半十线段AO 的长度十线段BC的长度。
【例2】 【原型题1】
3.14×4+3×4=24.56(dm)
【例2】 【原型题2】
3.14×6+6×5=48.84(dm)
【例2】 【变式题1】
3.14×10+6×10=91.4(cm)
【例2】 【变式题2】
周长:5×3.14×2=31.4(cm)
面积:4×4+3.14×1 =19.14(cm )
解析:作辅助线:
从图中可以看出:花瓣图形的周长等于4个半径为1cm的圆周长的一半加上4个半径为1cm的圆周长白的,即等于5个半径为1cm的圆的周长。花瓣图形的面积等于边长为4cm的正方形的面积加上1个半径为1cm的圆的面积。
【例2】 【拔高题】
3.14×20+20×4×4=382.8(cm)
3.14×20+20n×4=(62.8+80n)cm
解析:每一行两边都是1,每一个数等于它上方两数之和。第7行数字为1,6,15,20,15,6,1,第8行数字为1,7,21,35,35,21,7,1,所以第5个数是35。
同课章节目录
