《第10讲:数与形课件》(共17张PPT) 小升初人教版六年级数学专题复习
文档属性
| 名称 | 《第10讲:数与形课件》(共17张PPT) 小升初人教版六年级数学专题复习 |  | |
| 格式 | pptx | ||
| 文件大小 | 27.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 17:52:51 | ||
图片预览






文档简介
(共17张PPT)
小升初人教版六年级数学专题复习
第10讲:数与形
【经典案例】
【思路提示】
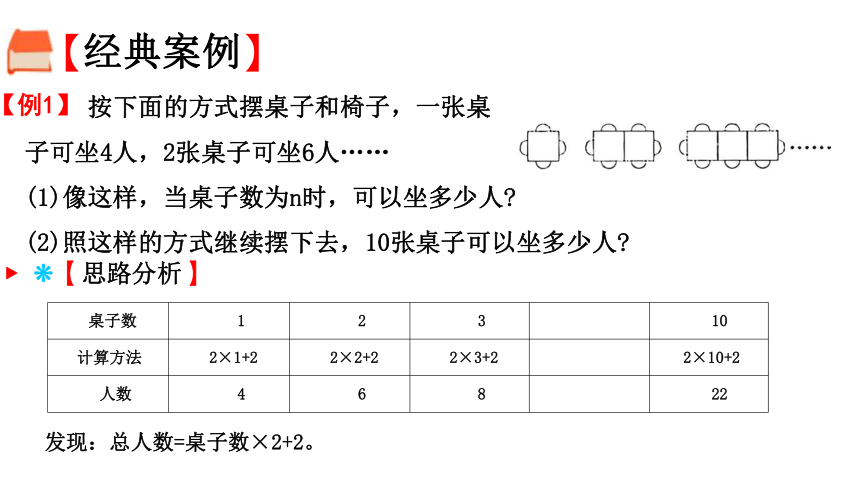
【例1】
按下面的方式摆桌子和椅子,一张桌
子可坐4人,2张桌子可坐6人……
(1)像这样,当桌子数为n时,可以坐多少人
(2)照这样的方式继续摆下去,10张桌子可以坐多少人
每多一张桌子就会多坐两个人。
【经典案例】
【思路分析】
【例1】
按下面的方式摆桌子和椅子,一张桌
子可坐4人,2张桌子可坐6人……
(1)像这样,当桌子数为n时,可以坐多少人
(2)照这样的方式继续摆下去,10张桌子可以坐多少人
观察上图,一张桌子坐4人,每增加一张桌子就多坐2人。第一张桌子坐了4人,增加(n-1)张桌子,就增加2(n-1)人,n张桌子一共可以坐4+2(n-1)=(2n+2)人。也可想象为左右两边的2人是固定的,一张桌子坐2人,所以n张桌子可坐(2+2n)人。
根据题意,也可以列表分析:
【经典案例】
【思路分析】
【例1】
按下面的方式摆桌子和椅子,一张桌
子可坐4人,2张桌子可坐6人……
(1)像这样,当桌子数为n时,可以坐多少人
(2)照这样的方式继续摆下去,10张桌子可以坐多少人
桌子数 1 2 3 10
计算方法 2×1+2 2×2+2 2×3+2 2×10+2
人数 4 6 8 22
发现:总人数=桌子数×2+2。
【经典案例】
【规范解答】
【例1】
按下面的方式摆桌子和椅子,一张桌
子可坐4人,2张桌子可坐6人……
(1)像这样,当桌子数为n时,可以坐多少人
(2)照这样的方式继续摆下去,10张桌子可以坐多少人
(1)当桌子数为n时,可以坐(2n+2)人。
(2)2×10+2=22(人)
答:10张桌子可以坐22人。
【经典案例】
【方法点拨】
【例1】
按下面的方式摆桌子和椅子,一张桌
子可坐4人,2张桌子可坐6人……
(1)像这样,当桌子数为n时,可以坐多少人
(2)照这样的方式继续摆下去,10张桌子可以坐多少人
数形结合法的实质是将抽象的数学语言与直观的图形结合起来,使代数问题几何化,几何问题代数化。
【原型题】
【强化训练】
【规范解答】
将正方形纸片按规律拼成如下的图案。
1.像这样,第n个图案中有多少张纸片
2.像这样,第几个图案中恰好有45张纸片
(1)(4n+1)张
(2)4n+1=45 n=11
答:(1)第n个图案中有(4n+1)张纸片。
(2)第11个图案中恰好有45张纸片.
【变式题】
【强化训练】
【规范解答】
如图,按照规律拼成下列图案,第8个图形是由多少根小棒拼成的
第8个图形是由108根小棒拼成的。
【拔高题】
【强化训练】
【规范解答】
用大小相同的正方形木块铺地面,第一次铺2块,以后每次都把前面一次铺的完全围起来(如图),以此类推。铺了n次后一共用了多少块木块
2n(2n—1)块
【经典案例】
【思路提示】
【例2】
自然数按下图的规律排列,则第28行第29列的数是多少
找出每行每列的排列规律是解决问题的关键。
【经典案例】
【规范解答】
【例2】
自然数按下图的规律排列,
则第28行第29列的数是多少
812
【经典案例】
【方法点拨】
【例2】
自然数按下图的规律排列,
则第28行第29列的数是多少
解答此类问题时,要先根据前面行数和列数的排列找出规律。
【原型题1】
【强化训练】
【规范解答】
李老师把自然数(0除外)按下面的样子排列。
1.照这样排下去,第7行有多少个数 第12行有多少个数
2.第1行到第7行一共有多少个数
1. 7×2-1=13(个) 12×2-1=23(个)
2. 1+3+5+7+9+11+13=49(个)
【原型题2】
【强化训练】
【规范解答】
下面“杨辉三角”中,第8行第5个数是多少
第8行第5个数是35
【变式题】
【强化训练】
【规范解答】
将自然数1,2,3,4,…按照
如图方式排列,依次在2,3,5,7,10, …数
的位置处拐弯。如果数字2算作第一次拐弯,
那么第50次拐弯的数字是多少
第50次拐弯处的数为:
1+2+4+6+…+50
=1+(2+50)×25÷2
=651
【拔高题】
【强化训练】
【规范解答】
你能利用下面的图发现(a-b)2=a2-2ab+b2这一公式吗 利用你所学的面积计算的知识,尝试探索一下。
(a-b) =a×a-a×b-a×b+b×b=a -2ab+b
不要放起自己
一步一个脚印
小升初思维特训
小升初人教版六年级数学专题复习
第10讲:数与形
【经典案例】
【思路提示】
【例1】
按下面的方式摆桌子和椅子,一张桌
子可坐4人,2张桌子可坐6人……
(1)像这样,当桌子数为n时,可以坐多少人
(2)照这样的方式继续摆下去,10张桌子可以坐多少人
每多一张桌子就会多坐两个人。
【经典案例】
【思路分析】
【例1】
按下面的方式摆桌子和椅子,一张桌
子可坐4人,2张桌子可坐6人……
(1)像这样,当桌子数为n时,可以坐多少人
(2)照这样的方式继续摆下去,10张桌子可以坐多少人
观察上图,一张桌子坐4人,每增加一张桌子就多坐2人。第一张桌子坐了4人,增加(n-1)张桌子,就增加2(n-1)人,n张桌子一共可以坐4+2(n-1)=(2n+2)人。也可想象为左右两边的2人是固定的,一张桌子坐2人,所以n张桌子可坐(2+2n)人。
根据题意,也可以列表分析:
【经典案例】
【思路分析】
【例1】
按下面的方式摆桌子和椅子,一张桌
子可坐4人,2张桌子可坐6人……
(1)像这样,当桌子数为n时,可以坐多少人
(2)照这样的方式继续摆下去,10张桌子可以坐多少人
桌子数 1 2 3 10
计算方法 2×1+2 2×2+2 2×3+2 2×10+2
人数 4 6 8 22
发现:总人数=桌子数×2+2。
【经典案例】
【规范解答】
【例1】
按下面的方式摆桌子和椅子,一张桌
子可坐4人,2张桌子可坐6人……
(1)像这样,当桌子数为n时,可以坐多少人
(2)照这样的方式继续摆下去,10张桌子可以坐多少人
(1)当桌子数为n时,可以坐(2n+2)人。
(2)2×10+2=22(人)
答:10张桌子可以坐22人。
【经典案例】
【方法点拨】
【例1】
按下面的方式摆桌子和椅子,一张桌
子可坐4人,2张桌子可坐6人……
(1)像这样,当桌子数为n时,可以坐多少人
(2)照这样的方式继续摆下去,10张桌子可以坐多少人
数形结合法的实质是将抽象的数学语言与直观的图形结合起来,使代数问题几何化,几何问题代数化。
【原型题】
【强化训练】
【规范解答】
将正方形纸片按规律拼成如下的图案。
1.像这样,第n个图案中有多少张纸片
2.像这样,第几个图案中恰好有45张纸片
(1)(4n+1)张
(2)4n+1=45 n=11
答:(1)第n个图案中有(4n+1)张纸片。
(2)第11个图案中恰好有45张纸片.
【变式题】
【强化训练】
【规范解答】
如图,按照规律拼成下列图案,第8个图形是由多少根小棒拼成的
第8个图形是由108根小棒拼成的。
【拔高题】
【强化训练】
【规范解答】
用大小相同的正方形木块铺地面,第一次铺2块,以后每次都把前面一次铺的完全围起来(如图),以此类推。铺了n次后一共用了多少块木块
2n(2n—1)块
【经典案例】
【思路提示】
【例2】
自然数按下图的规律排列,则第28行第29列的数是多少
找出每行每列的排列规律是解决问题的关键。
【经典案例】
【规范解答】
【例2】
自然数按下图的规律排列,
则第28行第29列的数是多少
812
【经典案例】
【方法点拨】
【例2】
自然数按下图的规律排列,
则第28行第29列的数是多少
解答此类问题时,要先根据前面行数和列数的排列找出规律。
【原型题1】
【强化训练】
【规范解答】
李老师把自然数(0除外)按下面的样子排列。
1.照这样排下去,第7行有多少个数 第12行有多少个数
2.第1行到第7行一共有多少个数
1. 7×2-1=13(个) 12×2-1=23(个)
2. 1+3+5+7+9+11+13=49(个)
【原型题2】
【强化训练】
【规范解答】
下面“杨辉三角”中,第8行第5个数是多少
第8行第5个数是35
【变式题】
【强化训练】
【规范解答】
将自然数1,2,3,4,…按照
如图方式排列,依次在2,3,5,7,10, …数
的位置处拐弯。如果数字2算作第一次拐弯,
那么第50次拐弯的数字是多少
第50次拐弯处的数为:
1+2+4+6+…+50
=1+(2+50)×25÷2
=651
【拔高题】
【强化训练】
【规范解答】
你能利用下面的图发现(a-b)2=a2-2ab+b2这一公式吗 利用你所学的面积计算的知识,尝试探索一下。
(a-b) =a×a-a×b-a×b+b×b=a -2ab+b
不要放起自己
一步一个脚印
小升初思维特训
同课章节目录
