第三单元第4讲 长方体和正方体表面积的计算 课件(共40张PPT)-五年级数学下册同步知识点讲练(人教版)
文档属性
| 名称 | 第三单元第4讲 长方体和正方体表面积的计算 课件(共40张PPT)-五年级数学下册同步知识点讲练(人教版) |  | |
| 格式 | pptx | ||
| 文件大小 | 52.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 19:46:43 | ||
图片预览










文档简介
(共40张PPT)
第4讲:
第三单元
长方体和正方体表面积的计算
表面积的意义与长方体表面积的计算方法
知识点①
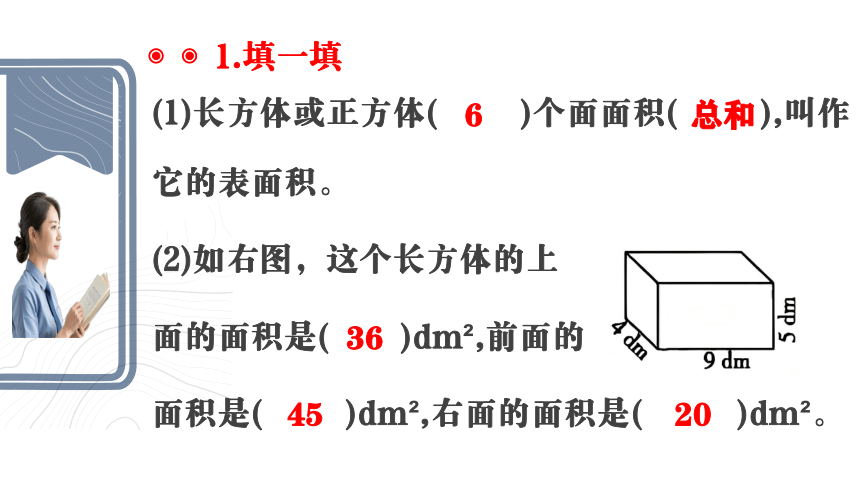
(1)长方体或正方体( )个面面积( ),叫作它的表面积。
(2)如右图,这个长方体的上
面的面积是( )dm ,前面的
面积是( )dm ,右面的面积是( )dm 。
1.填一填
6
总和
36
45
20
2.光明小学要举行少先队大队委员会选举,需要制作一个投票箱(如图),投票箱的长是4dm,宽是2dm,高是5dm。做这个投票箱需要硬纸板多少平方分米 (上面的孔大小忽略不计)
4×2=8(dm )
(1)上、下每个面面积:
(2)左、右每个面面积:
2×5=10(dm )
(3)前、后每个面面积:
4×5=20(dm )
(4)需要硬纸板的面积:
(8+10+20)×2=76(dm )
答:做这个投票箱需要硬纸板( )dm 。
76
举一反三1
(1)长方体有____个面,每个面都是____形(特殊情况下有两个相对的面是正方形)。
(2)计算长方体的表面积时,需要先求出____个面的总面积,公式为_____________。
(3)一个长方体的长是5cm,宽是3cm,高是4cm,它的表面积是____cm 。
1.填空题
6
长方
6
2(ab+ah+bh)
94
(1)一个长方体纸盒的表面积是指( )。
A.盒子的体积 B.盒子所有面的面积之和
C.盒子底面的面积 D.盒子侧面的面积之和
2.选择题。
B
(2)制作一个无盖的长方体鱼缸,需要计算( )个面的面积。
A.3 B.4
C.5 D.6
2.选择题。
C
(3)长方体的长、宽、高分别扩大到原来的2倍,表面积会扩大到原来的( )倍。
A.2 B.4
C.6 D.8
2.选择题。
B
(1)表面积和体积的单位都是长度单位。( )
(2)长方体的表面积计算公式是2(ab+ah+bh),其中(a,b,h)分别代表长、宽、高。( )
(3)一个长方体的长是6dm,宽是5dm,高是4dm,它的表面积是148平方分米。( )
3.判断题。
×
√
√
正方体的表面积
知识点②
4×4=16(dm )
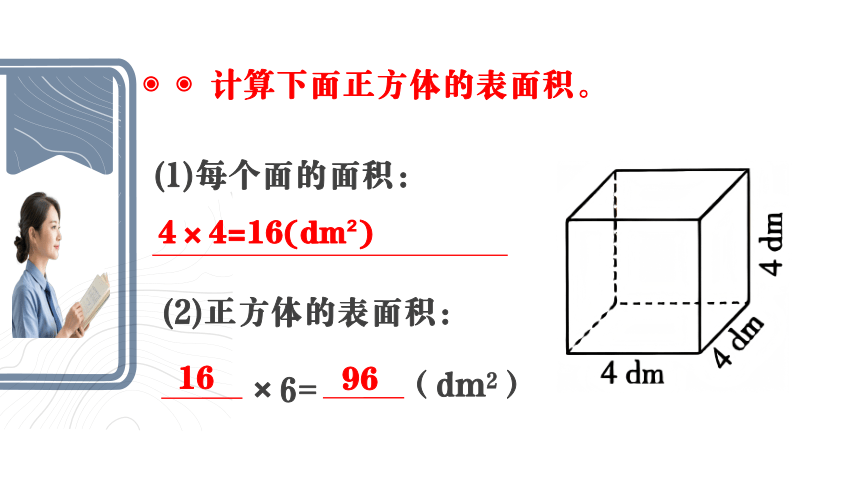
(1)每个面的面积:
计算下面正方体的表面积。
16
(2)正方体的表面积:
×6=
(dm2)
96
举一反三2
(1)一个正方体的棱长为4cm,它的表面积是____平方厘米。
(2)正方体的表面积是96cm ,它的棱长是______厘米。
(3)用纸板制作一个棱长为0.5m的正方体包装盒,至少需要________平方米的纸板。
1.填空题
96
4
1.5
(1)正方体的表面积计算公式是( )。
A.6a B.6a2
C.a3 D.12a
2.选择题。
B
(2)两个正方体的棱长分别是2cm和3cm,它们的表面积相差( )cm 。
A.12 B.30
C.54 D.24
2.选择题。
B
(3)一个正方体木块的棱长是20cm,若把它切成棱长为2cm的小正方体,表面积总和会增加( )cm 。
A.2400 B. 4800
C. 7200 D. 9600
2.选择题。
C
(1)正方体的表面积等于棱长的平方乘以6。( )
(2)棱长扩大2倍的正方体,表面积会扩大4倍。( )
(3)表面积相等的两个正方体,棱长一定相等。( )
3.判断题。
×
√
√
(1)正方体的棱长为4cm,求表面积。
4.看图计算题
6×42=96(cm2)
4cm
(2)正方体的展开图,每个面边长为5dm。原正方体的表面积是多少?
4.看图计算题
6×52=150(dm2)
(3)堆叠的正方体,每个小正方体棱长0.8m,共堆了3层(每层1个)。所有小正方体的表面积总和是多少?
4.看图计算题
3×6×0.82=11.52(m2)
长方体表面积的实际应用
知识点③
聪聪用长方形纸板制作一个长方体。他先把一张长16cm,宽7cm的纸板沿虚线折叠,做出了长方体相邻的2个面(如下图),然后再用纸板做出其他4个面,围成长方体。聪聪一共用了多少平方厘米的纸板 (接头处忽略不计)
16-10=6(cm)
(10×7+10×6+7×6)×2=344(cm )
答:聪聪一共用了344cm 的纸板。
举一反三3
(1)一个无盖的长方体玻璃鱼缸,长8分米,宽5分米,高6分米。制作这个鱼缸至少需要____平方分米的玻璃。
(2)学校要在长10米、宽4米、高3米的教室墙面(不含地面和天花板)贴瓷砖,贴瓷砖的面积是____平方米。
(3)用包装纸包装一个长15cm、宽10cm、高8cm的长方体礼盒,若接头处忽略不计,至少需要_____平方厘米的包装纸。
1.填空题
196
84
700
(1)粉刷一间长6米、宽5米、高4米的教室,需粉刷的面积是( )平方米。(门、窗面积共10平方米,不粉刷地面)
A.118 B.108
C.98 D.88
2.选择题。
B
(2)一个长方体通风管,横截面是边长2分米的正方形,长2米。制作一节这样的通风管需要铁皮( )平方分米。
A.16 B.160
C.16.8 D.168
2.选择题。
B
(3)一个长方体的长、宽、高分别扩大到原来的2倍,表面积会扩大到原来的( )倍。
A.2 B.4
C.6 D.8
2.选择题。
B
(1)长方体木箱的厚度会影响它的表面积计算。( )
(2)一个无盖的金鱼缸的表面积等于它的5个面的面积之和。( )
(3)棱长为a的正方体的表面积是6a ,所以所有正方体的表面积都是边长的平方的6倍。( )
3.判断题。
×
√
√
(1)一个长方体仓库,长12米,宽8米,高4米。仓库内壁(包括地面)需要粉刷水泥,如果每平方米需要水泥5千克,扣除门窗面积15平方米,一共需要多少千克水泥?
4.解决实际问题
总粉刷面积:
12×8+2×(12×4+8×4)-15
=96+160-15
=241(平方米)
需要水泥:241×5=1205(千克)
答: 一共需要1205千克水泥。
(2)某品牌磁带盒长12cm,宽7cm,高2cm。现将10盒磁带用包装纸包成一摞(如图,仅上下叠加),至少需要多少平方厘米的包装纸?
4.解决实际问题
叠加后长方体高为2×10=20cm,
表面积:
2×(12×7+12×20+7×20)
=2×544
=1088(cm )
答:至少需要1088平方厘米的包装纸。
(3)一个长方形蓄水池,长5米,宽3米,深2米。现要在池底和内壁铺满边长为2分米的正方形瓷砖,至少需要多少块瓷砖?
4.解决实际问题
池底面积:5×3=15(m )=1500(dm )
内壁面积:2×(5×2+3×2)×10=320(dm )
总需瓷砖:(1500+320)÷(2×2)=455(块)
答:至少需要455块瓷砖。
根据特殊长方体展开图求表面积
知识点④
如图,这个长方体底面是一个正方形,下图是这个长方体的侧面展开图,你能求出这个长方体的表面积吗
20÷4=5(cm);5×5×2+5×8×4=210(cm )
答:这个长方体的表面积是210cm 。
举一反三4
1.下图的纸板可以折成一个长方体纸盒(单位:厘米),这个长方体纸盒的表面积是多少平方厘米?
解决实际问题
14-2-2=10(厘米)
(10×6+10×2+6×2)×2
=(60+20+12)×2
=92×2
=184(平方厘米)
答:这个长方体纸盒的表面积是184平方厘米。
2.如图表示一个长方体展开图的前面、右面和上面(每个小方格表示1平方厘米)画出展开图的另外3个面,并算出长方体的表面积。
解决实际问题
这个长方体的长呈5厘米。宽是4厘米。高是2厘米。
(5×4+5×2+4×2)×2
=(20+10+8)×2
=38×2
=76(平方厘米)
答:长方体的表面积是76平方厘米。
如下图。
3.如图,是长方体的展开图,量出有关数据,求出这个长方体的表面积和体积。
解决实际问题
长方体的表面积:
(8×5+5×3+3×8)×2 长方体的体积:
=(40+15+24)×2 =8×5×3
=79×2 =40×3
=158(平方分米) =120(立方分米)
答:这个长方体的表面积是158平方分米,体积是120立方分米。
一个正方体木块的表面积是96dm ,把它沿虚线锯成大小相等的8个小正方体木块,表面积增加了多少平方分米
能力提升
96÷6×6=96(dm )
答:表面积增加了96dm 。
解决长方体或正方体表面积的实际问题时,需要根据实际情况,确定计算哪几个面的总面积。
第4讲:
第三单元
长方体和正方体表面积的计算
表面积的意义与长方体表面积的计算方法
知识点①
(1)长方体或正方体( )个面面积( ),叫作它的表面积。
(2)如右图,这个长方体的上
面的面积是( )dm ,前面的
面积是( )dm ,右面的面积是( )dm 。
1.填一填
6
总和
36
45
20
2.光明小学要举行少先队大队委员会选举,需要制作一个投票箱(如图),投票箱的长是4dm,宽是2dm,高是5dm。做这个投票箱需要硬纸板多少平方分米 (上面的孔大小忽略不计)
4×2=8(dm )
(1)上、下每个面面积:
(2)左、右每个面面积:
2×5=10(dm )
(3)前、后每个面面积:
4×5=20(dm )
(4)需要硬纸板的面积:
(8+10+20)×2=76(dm )
答:做这个投票箱需要硬纸板( )dm 。
76
举一反三1
(1)长方体有____个面,每个面都是____形(特殊情况下有两个相对的面是正方形)。
(2)计算长方体的表面积时,需要先求出____个面的总面积,公式为_____________。
(3)一个长方体的长是5cm,宽是3cm,高是4cm,它的表面积是____cm 。
1.填空题
6
长方
6
2(ab+ah+bh)
94
(1)一个长方体纸盒的表面积是指( )。
A.盒子的体积 B.盒子所有面的面积之和
C.盒子底面的面积 D.盒子侧面的面积之和
2.选择题。
B
(2)制作一个无盖的长方体鱼缸,需要计算( )个面的面积。
A.3 B.4
C.5 D.6
2.选择题。
C
(3)长方体的长、宽、高分别扩大到原来的2倍,表面积会扩大到原来的( )倍。
A.2 B.4
C.6 D.8
2.选择题。
B
(1)表面积和体积的单位都是长度单位。( )
(2)长方体的表面积计算公式是2(ab+ah+bh),其中(a,b,h)分别代表长、宽、高。( )
(3)一个长方体的长是6dm,宽是5dm,高是4dm,它的表面积是148平方分米。( )
3.判断题。
×
√
√
正方体的表面积
知识点②
4×4=16(dm )
(1)每个面的面积:
计算下面正方体的表面积。
16
(2)正方体的表面积:
×6=
(dm2)
96
举一反三2
(1)一个正方体的棱长为4cm,它的表面积是____平方厘米。
(2)正方体的表面积是96cm ,它的棱长是______厘米。
(3)用纸板制作一个棱长为0.5m的正方体包装盒,至少需要________平方米的纸板。
1.填空题
96
4
1.5
(1)正方体的表面积计算公式是( )。
A.6a B.6a2
C.a3 D.12a
2.选择题。
B
(2)两个正方体的棱长分别是2cm和3cm,它们的表面积相差( )cm 。
A.12 B.30
C.54 D.24
2.选择题。
B
(3)一个正方体木块的棱长是20cm,若把它切成棱长为2cm的小正方体,表面积总和会增加( )cm 。
A.2400 B. 4800
C. 7200 D. 9600
2.选择题。
C
(1)正方体的表面积等于棱长的平方乘以6。( )
(2)棱长扩大2倍的正方体,表面积会扩大4倍。( )
(3)表面积相等的两个正方体,棱长一定相等。( )
3.判断题。
×
√
√
(1)正方体的棱长为4cm,求表面积。
4.看图计算题
6×42=96(cm2)
4cm
(2)正方体的展开图,每个面边长为5dm。原正方体的表面积是多少?
4.看图计算题
6×52=150(dm2)
(3)堆叠的正方体,每个小正方体棱长0.8m,共堆了3层(每层1个)。所有小正方体的表面积总和是多少?
4.看图计算题
3×6×0.82=11.52(m2)
长方体表面积的实际应用
知识点③
聪聪用长方形纸板制作一个长方体。他先把一张长16cm,宽7cm的纸板沿虚线折叠,做出了长方体相邻的2个面(如下图),然后再用纸板做出其他4个面,围成长方体。聪聪一共用了多少平方厘米的纸板 (接头处忽略不计)
16-10=6(cm)
(10×7+10×6+7×6)×2=344(cm )
答:聪聪一共用了344cm 的纸板。
举一反三3
(1)一个无盖的长方体玻璃鱼缸,长8分米,宽5分米,高6分米。制作这个鱼缸至少需要____平方分米的玻璃。
(2)学校要在长10米、宽4米、高3米的教室墙面(不含地面和天花板)贴瓷砖,贴瓷砖的面积是____平方米。
(3)用包装纸包装一个长15cm、宽10cm、高8cm的长方体礼盒,若接头处忽略不计,至少需要_____平方厘米的包装纸。
1.填空题
196
84
700
(1)粉刷一间长6米、宽5米、高4米的教室,需粉刷的面积是( )平方米。(门、窗面积共10平方米,不粉刷地面)
A.118 B.108
C.98 D.88
2.选择题。
B
(2)一个长方体通风管,横截面是边长2分米的正方形,长2米。制作一节这样的通风管需要铁皮( )平方分米。
A.16 B.160
C.16.8 D.168
2.选择题。
B
(3)一个长方体的长、宽、高分别扩大到原来的2倍,表面积会扩大到原来的( )倍。
A.2 B.4
C.6 D.8
2.选择题。
B
(1)长方体木箱的厚度会影响它的表面积计算。( )
(2)一个无盖的金鱼缸的表面积等于它的5个面的面积之和。( )
(3)棱长为a的正方体的表面积是6a ,所以所有正方体的表面积都是边长的平方的6倍。( )
3.判断题。
×
√
√
(1)一个长方体仓库,长12米,宽8米,高4米。仓库内壁(包括地面)需要粉刷水泥,如果每平方米需要水泥5千克,扣除门窗面积15平方米,一共需要多少千克水泥?
4.解决实际问题
总粉刷面积:
12×8+2×(12×4+8×4)-15
=96+160-15
=241(平方米)
需要水泥:241×5=1205(千克)
答: 一共需要1205千克水泥。
(2)某品牌磁带盒长12cm,宽7cm,高2cm。现将10盒磁带用包装纸包成一摞(如图,仅上下叠加),至少需要多少平方厘米的包装纸?
4.解决实际问题
叠加后长方体高为2×10=20cm,
表面积:
2×(12×7+12×20+7×20)
=2×544
=1088(cm )
答:至少需要1088平方厘米的包装纸。
(3)一个长方形蓄水池,长5米,宽3米,深2米。现要在池底和内壁铺满边长为2分米的正方形瓷砖,至少需要多少块瓷砖?
4.解决实际问题
池底面积:5×3=15(m )=1500(dm )
内壁面积:2×(5×2+3×2)×10=320(dm )
总需瓷砖:(1500+320)÷(2×2)=455(块)
答:至少需要455块瓷砖。
根据特殊长方体展开图求表面积
知识点④
如图,这个长方体底面是一个正方形,下图是这个长方体的侧面展开图,你能求出这个长方体的表面积吗
20÷4=5(cm);5×5×2+5×8×4=210(cm )
答:这个长方体的表面积是210cm 。
举一反三4
1.下图的纸板可以折成一个长方体纸盒(单位:厘米),这个长方体纸盒的表面积是多少平方厘米?
解决实际问题
14-2-2=10(厘米)
(10×6+10×2+6×2)×2
=(60+20+12)×2
=92×2
=184(平方厘米)
答:这个长方体纸盒的表面积是184平方厘米。
2.如图表示一个长方体展开图的前面、右面和上面(每个小方格表示1平方厘米)画出展开图的另外3个面,并算出长方体的表面积。
解决实际问题
这个长方体的长呈5厘米。宽是4厘米。高是2厘米。
(5×4+5×2+4×2)×2
=(20+10+8)×2
=38×2
=76(平方厘米)
答:长方体的表面积是76平方厘米。
如下图。
3.如图,是长方体的展开图,量出有关数据,求出这个长方体的表面积和体积。
解决实际问题
长方体的表面积:
(8×5+5×3+3×8)×2 长方体的体积:
=(40+15+24)×2 =8×5×3
=79×2 =40×3
=158(平方分米) =120(立方分米)
答:这个长方体的表面积是158平方分米,体积是120立方分米。
一个正方体木块的表面积是96dm ,把它沿虚线锯成大小相等的8个小正方体木块,表面积增加了多少平方分米
能力提升
96÷6×6=96(dm )
答:表面积增加了96dm 。
解决长方体或正方体表面积的实际问题时,需要根据实际情况,确定计算哪几个面的总面积。
