第三单元第7讲 长方体和正方体体积的统一公式课件(共39张PPT)-五年级数学下册同步知识点讲练(人教版)
文档属性
| 名称 | 第三单元第7讲 长方体和正方体体积的统一公式课件(共39张PPT)-五年级数学下册同步知识点讲练(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 51.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-30 00:00:00 | ||
图片预览











文档简介
(共39张PPT)
第7讲:
第三单元
长方体和正方体体积的统一公式
长方体和正方体体积的统一公式
知识点①
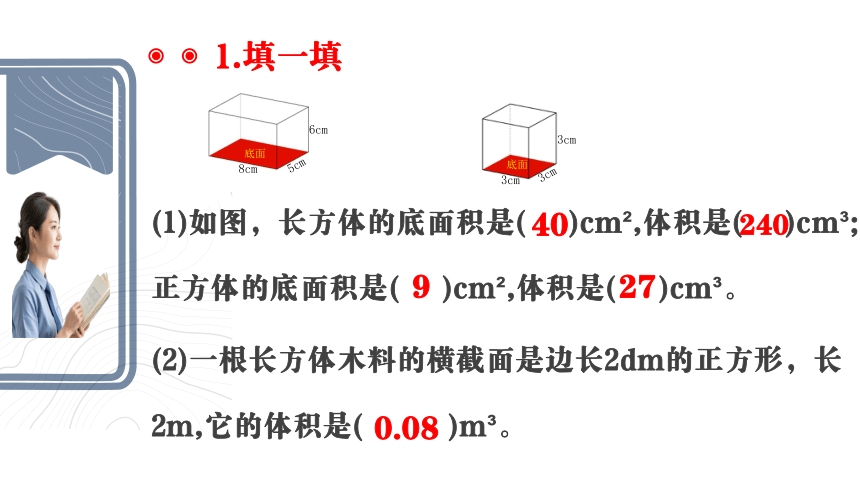
(1)如图,长方体的底面积是( )cm ,体积是( )cm ;正方体的底面积是( )cm ,体积是( )cm 。
(2)一根长方体木料的横截面是边长2dm的正方形,长2m,它的体积是( )m 。
1.填一填
40
240
9
27
0.08
8cm
5cm
6cm
底面
3cm
3cm
3cm
底面
(1)一根长方体钢材,横截面的面积是110cm ,长是5m,它的体积是( )cm 。
A.550 B.5500 C.55000
2. 选一选。
C
(2)有一根横截面面积是4dm ,长是30dm的长方体木料,如果将长截去5dm,那么截去部分的体积是( )dm 。
A.120 B.100 C.20
2. 选一选。
C
3. 某装饰公司订购500根方木,每根方木长5m,横截面是一个边长为0.3m的正方形。这些方木一共有多少立方米
解决问题
0.3×0.3×5×500=225(m )
答:这些方木一共有225m 。
4.手工课上,华华将一块体积为240cm 的橡皮泥做成了一个底面积是40cm 的长方体,做成的长方体的高是多少厘米
解决问题
240÷40=6(cm)
答:做成的长方体的高是6cm。
举一反三1
(1)一个长方体底面积是24cm ,高5cm,体积是______。
(2)正方体的棱长是6dm,它的体积可以表示为底面积×高,即______×______×______=______。
(3)一个长方体体积是120dm ,高8dm,底面积是______。
1.填空题
120cm
6dm
15dm
6dm
6dm
216dm
(1)长方体和正方体体积的统一公式是( )。
A.长+宽+高 B.底面积×高
C.表面积×高 D.棱长×棱长
2.选择题。
B
(2)一个长方体长5cm,宽4cm,高10cm,它的体积是( )。
A.200cm B.100cm
C.19cm D.400cm
2.选择题。
A
(3)正方体体积公式的正确表述是( )。
A.棱长×3 B.棱长×棱长
C.底面积×棱长 D.底面积×高
2.选择题。
D
(1)长方体体积=底面积×高,正方体体积不适用这个公式。( )
(2)底面积是25m 的长方体,若高2m,体积是50m 。( )
(3)体积为48cm 的正方体,底面积一定是16cm 。( )
3.判断题。
√
×
√
(1)一个鱼缸底面是边长4dm的正方形,水深3dm,鱼缸装了多少升水?
4.解决实际问题
4×4×3=48dm =48升
答:鱼缸装了48升水。
(2)工人用沙填长方体沙坑,沙坑长5m,宽2m,深0.4m,需要多少立方米的沙?
4.解决实际问题
5×2×0.4=4m
答:需要4立方米的沙。
(3)一个礼盒长20cm,宽15cm,高10cm。若礼盒内物品体积是底面积×高,求物品体积是多少立方厘米?
4.解决实际问题
20×15×10=3000cm
答:物品体积是3000立方厘米。
根据增加的表面积求体积
知识点②
解决问题
有一根长6m的长方体木料,把它锯成相同的4段,表面积比原来增加了180cm 。原来这根长方体木料的体积是多少立方厘米
6m=600cm
180÷[(4-1)×2]=30(cm ) 30×600=18000(cm )
答:原来这根长方体木料的体积是18000cm 。
举一反三2
(1)一个长方体,长8厘米,宽5厘米,高增加3厘米后,表面积增加了72平方厘米。原长方体的体积是______立方厘米。
(2)将一个正方体的棱长增加2厘米,表面积增加了120平方厘米。原正方体的体积是______立方厘米。
(3)一个长方体的高是6厘米,若将高减少2厘米,表面积减少了64平方厘米。原长方体的体积是_____立方厘米。
1.填空题
240
145
192
(1)一个长方体,长和宽分别是7厘米和4厘米。若高增加后,表面积增加了88平方厘米,新长方体的体积是( )。
A.224立方厘米 B.308立方厘米
C.352立方厘米 D.420立方厘米
2.选择题。
B
(2)一个正方体的表面积增加了96平方厘米,棱长增加了( )厘米。
A.2 B.3
C.4 D.5
2.选择题。
A
(3)一个长方体,若宽增加3厘米,表面积增加了60平方厘米,已知原长方体的长是5厘米,高是4厘米,原体积是( )。
A.60立方厘米 B.80立方厘米
C.100立方厘米 D.120立方厘米
2.选择题。
B
(1)若一个长方体的高增加2厘米,表面积增加了24平方厘米,则原长方体的体积一定是48立方厘米。( )
(2)正方体棱长增加后,体积的增幅一定大于表面积的增幅。( )
(3)已知长方体表面积增加的部分,一定能求出原体积。( )
3.判断题。
√
×
×
(1)小明用纸板做了一个无盖长方体盒子,底面长10厘米,宽8厘米,高是5厘米。如果他想让盒子的高增加3厘米,表面积会增加多少?新盒子的体积是多少?
4.解决实际问题
表面积增加:10×3×2+8×3×2=108平方厘米;
新体积:10×8×(5+3)=640立方厘米。
答:表面积会增加108平方厘米,新盒子的体积是640立方厘米
(1)小明用纸板做了一个无盖长方体盒子,底面长10厘米,宽8厘米,高是5厘米。如果他想让盒子的高增加3厘米,表面积会增加多少?新盒子的体积是多少?
4.解决实际问题
表面积增加:10×3×2+8×3×2=108平方厘米;
新体积:10×8×(5+3)=640立方厘米。
答:表面积会增加108平方厘米,新盒子的体积是640立方厘米
(2)一个正方体木块,表面积是150平方厘米。如果将它切成两个相同的长方体,表面积增加了50平方厘米。求原正方体的体积。
4.解决实际问题
原棱长:(150÷6)=5厘米
体积=5 =125立方厘米
答:原正方体的体积是125立方厘米。
(3)学校扩建一个长方体花坛,长和宽分别是6米和4米。扩建后,高增加了1米,表面积增加了40平方米。扩建后的花坛体积是多少立方米?
4.解决实际问题
原高:(40-2×6×1-2×4×1)÷(2×(6+4))=1米;
扩建后体积=6×4×(1+1)=48立方米。
答:扩建后的花坛体积是48立方米。
根据减少的表面积求体积
知识点③
一个长方体,如果高减少2dm就变成一个正方体,表面积减少了56dm 。原来长方体的体积是多少立方分米
56÷4÷2=7(dm);7×7×(7+2)=441(dm )
答:原来长方体的体积是441dm 。
举一反三3
(1)一个长方体,高减少3厘米后变成了正方体,表面积减少了72平方厘米。原长方体的体积是_____立方厘米。
(2)将一根长方体木料截去一个棱长2分米的小正方体后,表面积减少了32平方分米。原木料的体积是______立方分米。
(3)一个底面是正方形的长方体,若高减少5厘米,表面积减少120平方厘米,剩余部分是一个正方体。原长方体的体积是______立方厘米。
1.填空题
432
96
200
(1)一个长方体,若高截去4厘米后变成一个正方体,表面积减少64平方厘米。原长方体的体积是( )。
A.256cm B.288cm
C.320cm D.360cm
2.选择题。
B
(2)一个正方体被截去一个棱长3厘米的小正方体后(如图),表面积减少了54平方厘米。原正方体的体积是( )。
A.216cm B.125cm
C.343cm D.64cm
2.选择题。
A
(3)一个长方体木块,截去高2分米的部分后,表面积减少48平方分米,剩下的是一个正方体。原木块的体积是( )。
A.96dm B.144dm
C.192dm D.216dm
2.选择题。
B
(1)若一个长方体的高减少后变成正方体,减少的表面积等于减少部分的侧面积。( )
(2)截去一个长方体的一部分后,体积减少的量等于截去部分的体积。( )
(3)若一个长方体的底面是正方形,高减少后表面积减少的部分等于4个侧面的减少面积之和。( )
3.判断题。
√
√
√
工人师傅将一块长方体铁块截去一个棱长5厘米的小正方体后,表面积减少了200平方厘米。如果原铁块的长是20厘米,求它的体积。
4.解决实际问题
200÷4=50(平方厘米)。
50÷5=10(厘米)。
20×10×10=2000(立方厘米)
答:它的体积是2000立方厘米。
一个长方体的表面积是368cm ,底面积是40cm ,底面周长是36cm,这个长方体的体积是多少立方厘米
能力提升
(368-40×2)÷36=8(cm);40×8=320(cm )
答:这个长方体的体积是320cm 。
长方体的侧面展开是正方形,说明底面周长和高相等;长方体的侧面积除以底面周长等于高。
第7讲:
第三单元
长方体和正方体体积的统一公式
长方体和正方体体积的统一公式
知识点①
(1)如图,长方体的底面积是( )cm ,体积是( )cm ;正方体的底面积是( )cm ,体积是( )cm 。
(2)一根长方体木料的横截面是边长2dm的正方形,长2m,它的体积是( )m 。
1.填一填
40
240
9
27
0.08
8cm
5cm
6cm
底面
3cm
3cm
3cm
底面
(1)一根长方体钢材,横截面的面积是110cm ,长是5m,它的体积是( )cm 。
A.550 B.5500 C.55000
2. 选一选。
C
(2)有一根横截面面积是4dm ,长是30dm的长方体木料,如果将长截去5dm,那么截去部分的体积是( )dm 。
A.120 B.100 C.20
2. 选一选。
C
3. 某装饰公司订购500根方木,每根方木长5m,横截面是一个边长为0.3m的正方形。这些方木一共有多少立方米
解决问题
0.3×0.3×5×500=225(m )
答:这些方木一共有225m 。
4.手工课上,华华将一块体积为240cm 的橡皮泥做成了一个底面积是40cm 的长方体,做成的长方体的高是多少厘米
解决问题
240÷40=6(cm)
答:做成的长方体的高是6cm。
举一反三1
(1)一个长方体底面积是24cm ,高5cm,体积是______。
(2)正方体的棱长是6dm,它的体积可以表示为底面积×高,即______×______×______=______。
(3)一个长方体体积是120dm ,高8dm,底面积是______。
1.填空题
120cm
6dm
15dm
6dm
6dm
216dm
(1)长方体和正方体体积的统一公式是( )。
A.长+宽+高 B.底面积×高
C.表面积×高 D.棱长×棱长
2.选择题。
B
(2)一个长方体长5cm,宽4cm,高10cm,它的体积是( )。
A.200cm B.100cm
C.19cm D.400cm
2.选择题。
A
(3)正方体体积公式的正确表述是( )。
A.棱长×3 B.棱长×棱长
C.底面积×棱长 D.底面积×高
2.选择题。
D
(1)长方体体积=底面积×高,正方体体积不适用这个公式。( )
(2)底面积是25m 的长方体,若高2m,体积是50m 。( )
(3)体积为48cm 的正方体,底面积一定是16cm 。( )
3.判断题。
√
×
√
(1)一个鱼缸底面是边长4dm的正方形,水深3dm,鱼缸装了多少升水?
4.解决实际问题
4×4×3=48dm =48升
答:鱼缸装了48升水。
(2)工人用沙填长方体沙坑,沙坑长5m,宽2m,深0.4m,需要多少立方米的沙?
4.解决实际问题
5×2×0.4=4m
答:需要4立方米的沙。
(3)一个礼盒长20cm,宽15cm,高10cm。若礼盒内物品体积是底面积×高,求物品体积是多少立方厘米?
4.解决实际问题
20×15×10=3000cm
答:物品体积是3000立方厘米。
根据增加的表面积求体积
知识点②
解决问题
有一根长6m的长方体木料,把它锯成相同的4段,表面积比原来增加了180cm 。原来这根长方体木料的体积是多少立方厘米
6m=600cm
180÷[(4-1)×2]=30(cm ) 30×600=18000(cm )
答:原来这根长方体木料的体积是18000cm 。
举一反三2
(1)一个长方体,长8厘米,宽5厘米,高增加3厘米后,表面积增加了72平方厘米。原长方体的体积是______立方厘米。
(2)将一个正方体的棱长增加2厘米,表面积增加了120平方厘米。原正方体的体积是______立方厘米。
(3)一个长方体的高是6厘米,若将高减少2厘米,表面积减少了64平方厘米。原长方体的体积是_____立方厘米。
1.填空题
240
145
192
(1)一个长方体,长和宽分别是7厘米和4厘米。若高增加后,表面积增加了88平方厘米,新长方体的体积是( )。
A.224立方厘米 B.308立方厘米
C.352立方厘米 D.420立方厘米
2.选择题。
B
(2)一个正方体的表面积增加了96平方厘米,棱长增加了( )厘米。
A.2 B.3
C.4 D.5
2.选择题。
A
(3)一个长方体,若宽增加3厘米,表面积增加了60平方厘米,已知原长方体的长是5厘米,高是4厘米,原体积是( )。
A.60立方厘米 B.80立方厘米
C.100立方厘米 D.120立方厘米
2.选择题。
B
(1)若一个长方体的高增加2厘米,表面积增加了24平方厘米,则原长方体的体积一定是48立方厘米。( )
(2)正方体棱长增加后,体积的增幅一定大于表面积的增幅。( )
(3)已知长方体表面积增加的部分,一定能求出原体积。( )
3.判断题。
√
×
×
(1)小明用纸板做了一个无盖长方体盒子,底面长10厘米,宽8厘米,高是5厘米。如果他想让盒子的高增加3厘米,表面积会增加多少?新盒子的体积是多少?
4.解决实际问题
表面积增加:10×3×2+8×3×2=108平方厘米;
新体积:10×8×(5+3)=640立方厘米。
答:表面积会增加108平方厘米,新盒子的体积是640立方厘米
(1)小明用纸板做了一个无盖长方体盒子,底面长10厘米,宽8厘米,高是5厘米。如果他想让盒子的高增加3厘米,表面积会增加多少?新盒子的体积是多少?
4.解决实际问题
表面积增加:10×3×2+8×3×2=108平方厘米;
新体积:10×8×(5+3)=640立方厘米。
答:表面积会增加108平方厘米,新盒子的体积是640立方厘米
(2)一个正方体木块,表面积是150平方厘米。如果将它切成两个相同的长方体,表面积增加了50平方厘米。求原正方体的体积。
4.解决实际问题
原棱长:(150÷6)=5厘米
体积=5 =125立方厘米
答:原正方体的体积是125立方厘米。
(3)学校扩建一个长方体花坛,长和宽分别是6米和4米。扩建后,高增加了1米,表面积增加了40平方米。扩建后的花坛体积是多少立方米?
4.解决实际问题
原高:(40-2×6×1-2×4×1)÷(2×(6+4))=1米;
扩建后体积=6×4×(1+1)=48立方米。
答:扩建后的花坛体积是48立方米。
根据减少的表面积求体积
知识点③
一个长方体,如果高减少2dm就变成一个正方体,表面积减少了56dm 。原来长方体的体积是多少立方分米
56÷4÷2=7(dm);7×7×(7+2)=441(dm )
答:原来长方体的体积是441dm 。
举一反三3
(1)一个长方体,高减少3厘米后变成了正方体,表面积减少了72平方厘米。原长方体的体积是_____立方厘米。
(2)将一根长方体木料截去一个棱长2分米的小正方体后,表面积减少了32平方分米。原木料的体积是______立方分米。
(3)一个底面是正方形的长方体,若高减少5厘米,表面积减少120平方厘米,剩余部分是一个正方体。原长方体的体积是______立方厘米。
1.填空题
432
96
200
(1)一个长方体,若高截去4厘米后变成一个正方体,表面积减少64平方厘米。原长方体的体积是( )。
A.256cm B.288cm
C.320cm D.360cm
2.选择题。
B
(2)一个正方体被截去一个棱长3厘米的小正方体后(如图),表面积减少了54平方厘米。原正方体的体积是( )。
A.216cm B.125cm
C.343cm D.64cm
2.选择题。
A
(3)一个长方体木块,截去高2分米的部分后,表面积减少48平方分米,剩下的是一个正方体。原木块的体积是( )。
A.96dm B.144dm
C.192dm D.216dm
2.选择题。
B
(1)若一个长方体的高减少后变成正方体,减少的表面积等于减少部分的侧面积。( )
(2)截去一个长方体的一部分后,体积减少的量等于截去部分的体积。( )
(3)若一个长方体的底面是正方形,高减少后表面积减少的部分等于4个侧面的减少面积之和。( )
3.判断题。
√
√
√
工人师傅将一块长方体铁块截去一个棱长5厘米的小正方体后,表面积减少了200平方厘米。如果原铁块的长是20厘米,求它的体积。
4.解决实际问题
200÷4=50(平方厘米)。
50÷5=10(厘米)。
20×10×10=2000(立方厘米)
答:它的体积是2000立方厘米。
一个长方体的表面积是368cm ,底面积是40cm ,底面周长是36cm,这个长方体的体积是多少立方厘米
能力提升
(368-40×2)÷36=8(cm);40×8=320(cm )
答:这个长方体的体积是320cm 。
长方体的侧面展开是正方形,说明底面周长和高相等;长方体的侧面积除以底面周长等于高。
