数学泸科版七年级上册余角和补角课件

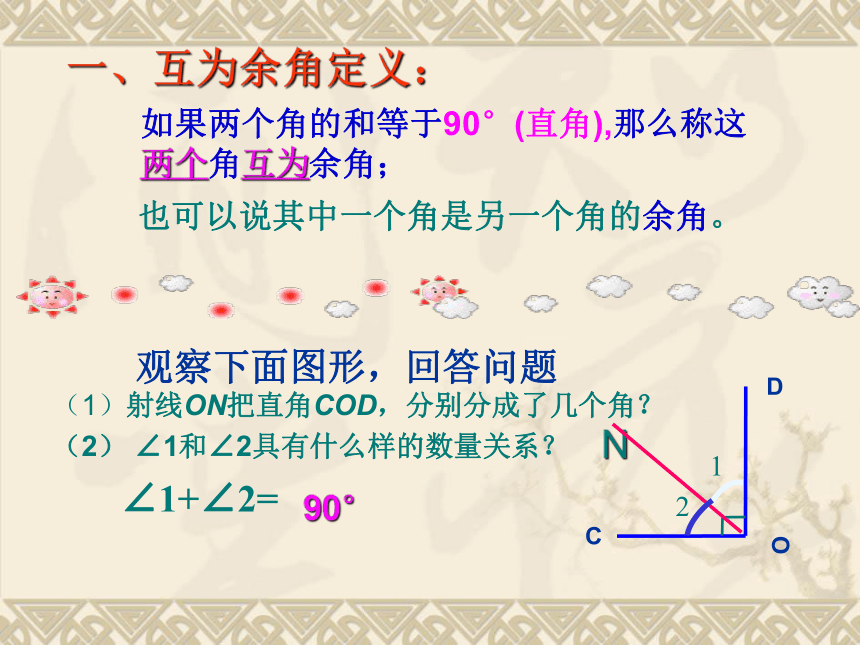
课件18张PPT。余角和补角观察下面图形，回答问题（1）射线ON把直角COD，分别分成了几个角？
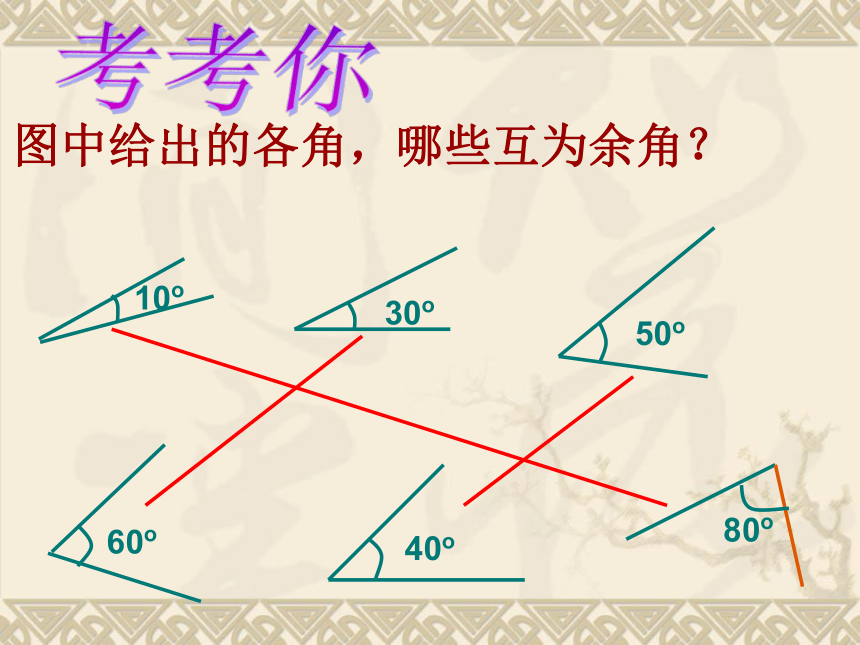
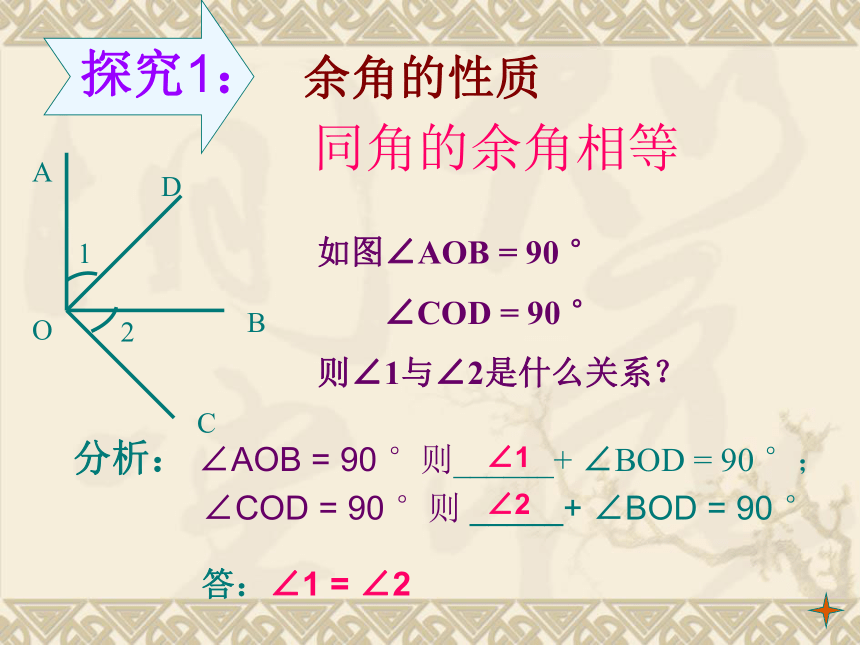
（2） ∠1和∠2具有什么样的数量关系？∠1+∠2=90°如果两个角的和等于90°(直角),那么称这两个角互为余角；一、互为余角定义：也可以说其中一个角是另一个角的余角。图中给出的各角，哪些互为余角？10o30o60o80o50o40o考考你分析： ∠AOB = 90 °则______+ ∠BOD = 90 °；同角的余角相等余角的性质∠COD = 90 °则 _____+ ∠BOD = 90 °答：∠1 = ∠2∠1∠2 如图∠1 与∠2互余，∠３ 与∠４互余 ，如果∠1＝∠３那么∠2与∠４相等吗？为什么？余角的性质答：∠2与∠４相等，等角的余角相等∠1∠3 +∠4=90°，即∠4=90°－ ∠3∠2 =∠4∵ ∠1 与∠2互余，
∴ ∠1 +∠2=90°，即 ∠2= 90 °－＿＿；∵ ∠3与∠4互余 ，
∴＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿＿；∵ ∠1 =∠3，
∴ 90°－∠1 =90°－ ∠3
即：＿＿＿＿＿＿＿＿。理由如下：探究2同角或等角的余角相等 二、余角性质：1. 观察下面图形，回答以下问题？（1）射线OM把平角AOB，分成了几个角？（2）∠3和∠4具有什么样的数量关系？∠3+∠4=180°观察如果两个角的和等于180°(平角),那么称这两个角互为补角；也可以说其中一个角是另一个角的补角.三、互为补角定义：图中给出的各角，那些互为补角？10o30o60o80o100o120o150o170o考考你 如图∠1 与∠2互补，∠1 与∠3互补 ，那么∠2与∠3相等吗？为什么？补角的性质∵ ∠1 与∠2互补，
∴ ∠2= 180 °－＿＿＿；∠1答：∠2与∠3相等。同角的补角相等∵ ∠1与∠3互补 ，
∴＿＿＿＿＿＿＿＿＿＿＿。∠3 = 180° －∠1∴＿＿＿＿＿＿＿＿。∠2=∠3探究3理由如下：如果∠1与∠2互补，∠3与∠4互补，∠1＝∠3，那么∠2与∠4有什么关系？为什么？ 解: ∵ ∠1 与∠2互补，
∴ ＿＿＿＿＿＿＿＿＿＿＿；
∵ ∠3 与∠4互补，
∴ ＿＿＿＿＿＿＿＿＿＿；
又 ∵ ∠1＝∠3,
∴ ＿＿＿＿＿＿＿＿＿＿＿＿，
　 即＿＿＿＿＿＿＿＿。∠2 =180－ ∠1∠4= 180°－ ∠3180°－ ∠1= 180°－ ∠3∠2=∠4补角的性质等角的补角相等探究4
同角或等角的补角相等四、补角性质：∠1+∠2=90°∠1+∠2=180°同角或等角的余角相等同角或等角的补角相等．我来试一试：85°175°58°148°117°37′180°－∠ ?109°21′27°37′∠ ? （ ∠ ? <90 ° ）的余角是 　 。 　 　 ∠ ?的补角是 　 。
则一个角的补角比它的余角大　 。90°－ ∠ ? 90°归纳：90°－X 180°－X19°21′已知一个角的补角是它的余角的4倍，求这个角的度数。解：设这个角为x度,则它的余角是 　度,
它的补角是 度.(90-x)(180-x)依题意得　180-x=4(90-x)解方程得：　　x = 60即：这个角的度数为60o范例讲解练习：一个角的补角是它的3倍，则这个角是＿＿＿＿＿。45o提示：设这个角为X度，则X+3X=180如图，E、F是直线DG上两点
∠1 = ∠2,∠3 = ∠4 = 90 °找出图中相等的角并说明理由。答：∠AEF = ∠CFE，∠5 = ∠6。练一练理由如下：
∵ ∠AEF+ ∠4 = 180 °，
∠CFE+ ∠3 = 180 °，
∵ ∠3 = ∠4 = 90 °，
∴ ∠AEF = ∠CFE（等角的补角相等）；∴ ∠5 = ∠6（等角的余角相等）.∵ ∠5+ ∠1 = 90 °，∠6+ ∠2= 90 °，∵ ∠1 = ∠2 ，123456余角、补角的概念：余角、补角的性质：（1） 和为90°的两个角称互为余角；
（2） 和为180°的两个角称互为补角；（1） 同角或等角的余角相等；
（2） 同角或等角的补角相等；今天我们学了什么？
课本141页 5、6题 作业如图，已知AOB是一直线，OC是∠ AOB的平分线， ∠ DOE是直角，图中哪些角相等？哪些角互余？哪些角互补？（至少三对）B讨论答：相等的角有： ∠AOC= ∠BOC= ∠DOE = 90° ；
∠ 1= ∠ 4； ∠ 2= ∠ 3；互余的角有： ∠ 1 + ∠ 2= 90° ；
∠ 3 + ∠ 4= 90° ；
∠ 1 + ∠ 3= 90° ；
∠ 2 + ∠ 4= 90° ； 互补的角有： ∠AOC +∠BOC = 180°；
∠ 4+ ∠ EOB= 180°；
∠ 1+ ∠ EOB= 180°；
∠ 2+ ∠ AOD= 180°；
∠ 3+ ∠ AOD= 180°；
等等