2025年九年级中考数学三轮冲刺训练隐圆训练(含解析)
文档属性
| 名称 | 2025年九年级中考数学三轮冲刺训练隐圆训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 924.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级中考数学三轮冲刺训练隐圆训练
一、选择题
1.如图,在边长为2的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足
AE=CD,连接BE、AD相交于点P,则线段CP的最小值为( )
A.1 B.2 C. D.21
2.如图,⊙O的半径为1,弦AB=1,点P为优弧上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是( )
A. B. C. D.
3.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
A.22 B. C. D.
4.如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为( )
A.π B.π C.π D.π
5.直线y=x+4分别与x轴、y轴相交于点M,N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交于点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )
A.22 B.3﹣2 C. D.1
6.如图,在矩形ABCD中,AB=8,BC=6,点P在矩形的内部,连接PA,PB,PC,若∠PBC=∠PAB,则PC的最小值是( )
A.6 B.3 C.24 D.44
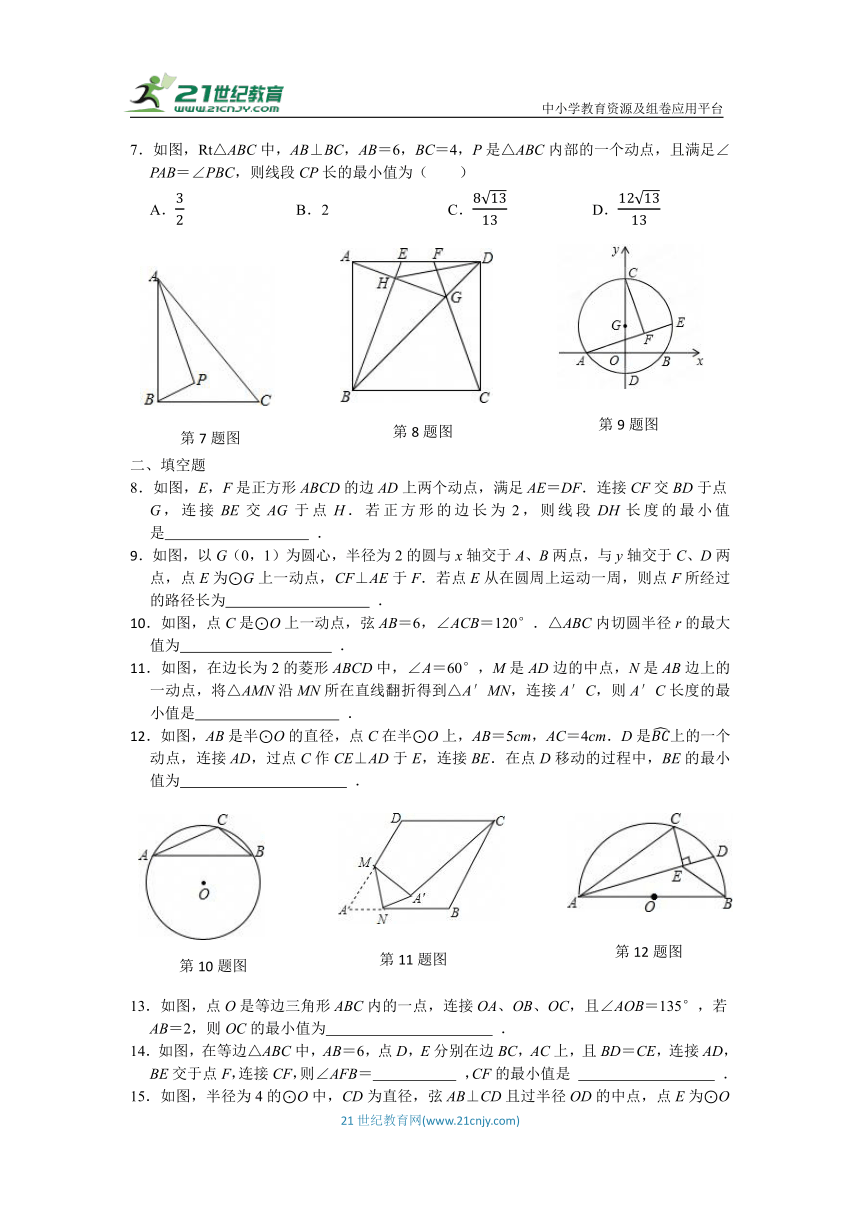
7.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. B.2 C. D.
二、填空题
8.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
9.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.若点E从在圆周上运动一周,则点F所经过的路径长为 .
10.如图,点C是⊙O上一动点,弦AB=6,∠ACB=120°.△ABC内切圆半径r的最大值为 .
11.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
12.如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为 .
13.如图,点O是等边三角形ABC内的一点,连接OA、OB、OC,且∠AOB=135°,若AB=2,则OC的最小值为 .
14.如图,在等边△ABC中,AB=6,点D,E分别在边BC,AC上,且BD=CE,连接AD,BE交于点F,连接CF,则∠AFB= ,CF的最小值是 .
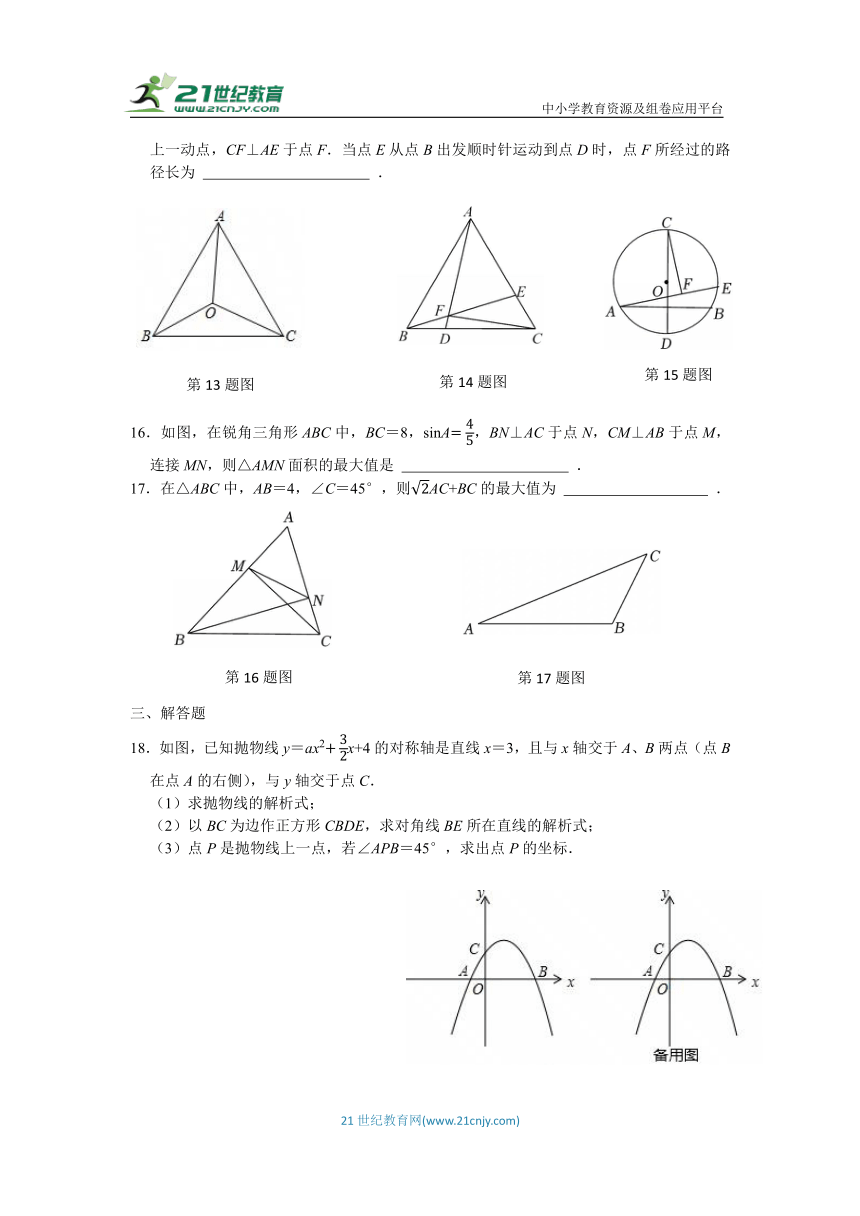
15.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为 .
16.如图,在锐角三角形ABC中,BC=8,sinA,BN⊥AC于点N,CM⊥AB于点M,连接MN,则△AMN面积的最大值是 .
17.在△ABC中,AB=4,∠C=45°,则AC+BC的最大值为 .
三、解答题
18.如图,已知抛物线y=ax2x+4的对称轴是直线x=3,且与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)以BC为边作正方形CBDE,求对角线BE所在直线的解析式;
(3)点P是抛物线上一点,若∠APB=45°,求出点P的坐标.
19.如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
20.如图,在梯形ABCD中,AD∥BC,∠A=90°,AB=6,BC=10,AD=7,点P在边AD上运动(不与点A,D重合),E是边AB上一点,连接PC,PE,EC.
(1)当点B,P关于直线EC对称时,求BE的长;
(2)设BE=a,若存在唯一点P,使∠EPC=90°,求a,AP的值.
参考答案
一、选择题
1.【解答】解:∵CD=AE,BC=AC,
∴BD=CE,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠APE=∠ABE+∠BAD,∠APE=∠BPD,∠ABE+∠CBE=60°,
∴∠BPD=∠APE=∠ABC=60°,
∴∠APB=120°,
∴点P的运动轨迹是,∠AOB=120°,连接CO,
∵OA=OB,CA=CB,OC=OC,
∴△AOC≌△BOC(SSS),
∴∠OAC=∠OBC,∠ACO=∠BCO=30°,
∵∠AOB+∠ACB=180°,
∴∠OAC+∠OBC=180°,
∴∠OAC=∠OBC=90°,
∴OC=AC÷cos30°=4,OAOC=2,
∴OP=2,
∵PC≥OC﹣OP,
∴PC≥2,
∴PC的最小值为2.
故选:B.
2.【解答】解:连接OA、OB,如图1,
∵OA=OB=1,AB=1,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB∠AOB=30°,
∵AC⊥AP,
∴∠C=60°,
∵AB=1,要使△ABC的面积最大,则点C到AB的距离最大,
∵∠ACB=60°,点C在⊙D上,
∴∠ADB=120°,
如图2,作△ABC的外接圆D,
当点C在优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为AB2,
∴△ABC的最大面积为.
故选:D.
3.【解答】解:连接AE,如图1,
∵∠BAC=90°,AB=AC,BC=2,
∴AB=AC=2,
∵AD为直径,
∴∠AED=90°,
∴∠AEB=90°,
∴点E在以AB为直径的⊙O上,
∵⊙O的半径为1,
连接OE,OC,
∴OEAB=1
在Rt△AOC中,
∵OA=1,AC=2,
∴OC,
由于OC,OE=1是定值,
点E在线段OC上时,CE最小,如图2,
∴CE=OC﹣OE1,
即线段CE长度的最小值为1.
故选:C.
4.【解答】解:如图,连OI,PI,AI,
∵△OPH的内心为I,
∴∠IOP=∠IOA,∠IPO=∠IPH,
∴∠PIO=180°﹣∠IPO﹣∠IOP=180°(∠HOP+∠OPH),
而PH⊥OA,即∠PHO=90°,
∴∠PIO=180°(∠HOP+∠OPH)=180°(180°﹣90°)=135°,
又∵OP=OA,OI公共,
而∠IOP=∠IOA,
∴△OPI≌△OAI,
∴∠AIO=∠PIO=135°,
所以点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上;
过A、I、O三点作⊙O′,如图,连O′A,O′O,
在优弧AO取点P′,连P′A,P′O,
∵∠AIO=135°,
∴∠AP′O=180°﹣135°=45°,
∴∠AO′O=90°,而OA=2cm,
∴O′OOA2,
∴弧OA的长π(cm),
所以内心I所经过的路径长为 πcm.
故选:B.
5.【解答】解:在△MOC和△NOA中,
,
∴△MOC≌△NOA,
∴∠CMO=∠ANO,
∵∠CMO+∠MCO=90°,∠MCO=∠NCP,
∴∠NCP+∠CNP=90°,
∴∠MPN=90°
∴MP⊥NP,
在正方形旋转的过程中,同理可证,∴∠CMO=∠ANO,可得∠MPN=90°,MP⊥NP,
∴P在以MN为直径的圆上,
∵M(﹣4,0),N(0,4),
∴圆心G为(﹣2,2),半径为2,
∵PG﹣GC≤PC,
∴当圆心G,点P,C(0,2)三点共线时,PC最小,
∵GN=GM,CN=CO=2,
∴GCOM=2,
这个最小值为GP﹣GC=22.
故选:A.
6.【解答】解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PBC=∠PAB,
∴∠PAB+∠PBA=90°,
∴∠APB=90°,
∴点P在以AB为直径的圆上运动,设圆心为O,连接OC交⊙O于P,此时PC最小,
∵OC2,
∴PC的最小值为24,
故选:C.
7.【解答】解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC,
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴OP=OA=OB(直角三角形斜边中线等于斜边一半),
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在Rt△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC5,
∴PC=OC﹣OP=5﹣3=2.
∴PC最小值为2.
故选:B.
二、填空题
8.【解答】解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°﹣90°=90°,
取AB的中点O,连接OH、OD,
则OH=AOAB=1,
在Rt△AOD中,OD,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
最小值=OD﹣OH1.
(解法二:可以理解为点H是在Rt△AHB,AB直径的半圆上运动当O、H、D三点共线时,DH长度最小)
故答案为:1.
9.【解答】解:连接AG.
∵CF⊥AE于F,
∴AO,
在直角△AOC中,AC2,
则以AC为直径的圆的周长是2π.
故答案为:2π.
10.【解答】解:当点C为弧AB的中点时,△ABC内切圆半径r的最大,如图,连接OC交AB于D点,⊙M为△ABC的内切圆,作ME⊥AC于E点,
∵点C为弧AB的中点,
∴OC⊥AB,AD=BDAB=6,AC=BC,
∴点M在CD上,
∴ME和MD都为⊙M的半径,
设ME=MD=r,
∵∠ACB=120°,
∴∠A=30°,∠ACD=60°,
在Rt△ACD中,CDAD,
在Rt△CEM中,∠ECM=60°,∠CME=30°,
∴CEEMr,
∴CM=2CEr,
∵CM+DM=CD,
∴r+r,
∴r=6﹣3,
故答案为:6﹣3.
11.【解答】解:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠FDM=60°,
∴∠FMD=30°,
∴FDMD,
∴FM=DM×cos30°,
∴MC,
∴A′C=MC﹣MA′1.
故答案为:1.
12.【解答】解:如图,取AC的中点为O',连接BO′、BC.
∵CE⊥AD,
∴∠AEC=90°,
∴在点D移动的过程中,点E在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AC=4cm,AB=5cm,
∴BC3cm,
在Rt△BCO′中,BO′cm,
∵O′E+BE≥O′B,
∴当O′、E、B共线时,BE的值最小,最小值为O′B﹣O′E2(cm),
故答案为:()cm.
13.【解答】解:如图,作△ABO的外接圆⊙G.连接AG,BG,OG,CG,CG交AB于J.
∵∠AOB=135°,
∴∠AGB=90°,
∵AB=2,
∴AG=GB=OG,
∵GA=GB,CA=CB,
∴CG垂直平分线段AB,
∴AJ=JB=1,
∴CJ,GJ=AJ=BJ=1,
∴CG=1,
∴OC≥CG﹣OG,
∴OC≥1,
∴OC的最小值为1.
故答案为:1.
14.【解答】解:如图,∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠BAC=∠BCE=60°,
∵BD=CE,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
又∵∠AFE=∠BAD+∠ABE,
∴∠AFE=∠CBE+∠ABE=∠ABC,
∴∠AFE=60°,
∴∠AFB=120°,
∴点F的运动轨迹是O为圆心,OA为半径的弧上运动(∠AOB=120°,OA=2),
连接OC交⊙O于N,当点F与N重合时,CF的值最小,最小值=OC﹣ON=422.
故答案为:120°,2.
15.【解答】解:∵CF⊥AE,
∴∠AFC=90°,
∴点F在以AC为直径的圆上运动,
以AC为直径画半圆AC,连接OA,
当点E与B重合时,此时点F与G重合,
当点E与D重合时,此时点F与A重合,
∴点E从点B出发顺时针运动到点D时,点F所经过的路径长为的长,
∵点G为OD的中点,
∴OGODOA=2,
∵OG⊥AB,
∴∠AOG=60°,AG=2,
∵OA=OC,
∴∠ACG=30°,
∴AC=2AG=4,
∴所在圆的半径为2,圆心角为60°,
∴的长为,
故答案为:.
16.【解答】解:画出△ABC的外接圆⊙O,连接OB,
∵BC=8,sinA,
∴点A在优弧BC上运动,
当A'O⊥BC时,△A'BC的面积最大,
∴BH=4,
∵∠BOH=∠BAC,
∴BO=5,OH=3,
∴AH=8,cos∠BOH,
∴S△ABC最大为32,
∵CM⊥AB,
∴cos∠MAC,
∵AB=AC,AM=AN,∠MAN=∠BAC,
∴△AMN∽△ABC,
∴,
∴,
∴S△AMN,
故答案为:.
17.【解答】解:过点B作BD⊥AC于点D,
∵∠C=45°,
∴△BCD为等腰直角三角形,
∴BD=CD,
设BD=CD=a,延长AC至点F,使得CF=a,
∵tan∠AFB,
作△ABF的外接圆⊙O,过点O作OE⊥AB于点E,则AEAB=2,∠AOE=∠AFB,
∴tan∠AOE,
∴OE=4,OA,
∴BC(ACBC)(AC+CF)(OA+OF),
∴BC的最大值为4.
故答案为:.
三、解答题
18.【解答】解:(1)∵抛物线的对称轴是直线x=3
∴3,解得:a
∴抛物线的解析式为yx2x+4
(2)当yx2x+4=0时,解得:x1=﹣2,x2=8
∴A(﹣2,0),B(8,0)
∴AB=10,OB=8
当x=0时,yx2x+4=4
∴C(0,4),OC=4
①如图1,若点E在第一象限,过点E作EF⊥y轴于点F
∴∠CFE=∠BOC=90°
∵四边形CBDE是正方形
∴∠BCE=90°,BC=CE
∴∠BCO+∠OBC=∠BCO+∠FCE=90°
∴∠OBC=∠FCE
在△FCE与△OBC中
∴△FCE≌△OBC(AAS)
∴FC=OB=8,EF=OC=4
∴OF=OC+FC=12
∴E(4,12)
设直线BE解析式为:y=kx+b
∴ 解得:
∴直线BE解析式为y=﹣3x+24
②如图2,若点E在第三象限,过点E作EF⊥y轴于点F
同理可证:△FCE≌△OBC(AAS)
∴FC=OB=8,EF=OC=4
∴OF=FC﹣OC=8﹣4=4
∴E(﹣4,﹣4)
设直线BE解析式为:y=k'x+b'
∴ 解得:
∴直线BE解析式为yx
综上所述,直线BE解析式为y=﹣3x+24 或yx
(3)以AB为斜边作等腰Rt△AGB,则AG=BG,∠AGB=90°
以点G为圆心、AG长为半径画圆,则点P在优弧AB上时总有∠APB=45°.
如图3,若点G在第一象限,⊙G与抛物线交点只有A、B,即没有满足条件的点P使∠APB=45°
如图4,若点G在第四象限,过点G作GM⊥x轴于点M
∴AM=BM=GMAB=5,
∴G(3,﹣5)
设P(p,p2p+4)
∵PG=AGAB=5,
∴PG2=50 可得方程:(p﹣3)2+(p2p+4+5)2=50,
∴(p﹣3)2[(p﹣3)2﹣45]2=50,
令p﹣3=t,
∴t2(t2﹣45)2=50,
解得t2=49或t2=25,
∴p1=﹣4,p2=10,p3=﹣2(即点A,舍去),p4=8(即点B,舍去)
∴p2p+4=﹣6
∴点P坐标为(﹣4,﹣6)或(10,﹣6)
19.【解答】解:(1)如图1中,
在四边形ABCD中,∵∠A+∠B+∠C+∠D=360°,∠B=60°,∠D=30°,
∴∠A+∠C=360°﹣60°﹣30°=270°.
(2)如图2中,结论:DB2=DA2+DC2.
理由:连接BD.以BD为边向下作等边三角形△BDQ.
∵∠ABC=∠DBQ=60°,
∴∠ABD=∠CBQ,
∵AB=BC,DB=BQ,
∴△ABD≌△CBQ(SAS),
∴AD=CQ,∠A=∠BCQ,
∵∠A+∠BCD=∠BCQ+∠BCD=270°,
∴∠DCQ=90°,
∴DQ2=DC2+CQ2,
∵CQ=DA,DQ=DB,
∴DB2=DA2+DC2.
(3)如图3中,连接AC,将△ACE绕点A顺时针旋转60°得到△ABR,连接RE.
则△AER是等边三角形,∵EA2=EB2+EC2,EA=RE,EC=RB,
∴RE2=RB2+EB2,
∴∠EBR=90°,
∴∠RAE+∠RBE=150°,
∴∠ARB+∠AEB=∠AEC+∠AEB=210°,
∴∠BEC=150°,
∴点E的运动轨迹在O为圆心的圆上,在⊙O上取一点K,连接KB,KC,OB,OC,
∵∠K+∠BEC=180°,
∴∠K=30°,∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=1,
∴点E的运动路径.
20.【解答】解:(1)如图1中,作CM⊥AD于M.设BE=x.
∵△CEP是由△CEB翻折得到,
∴CP=CB=10,PE=EB=x,
∵∠A=90°,AD∥BC,
∴∠A=∠B=∠M=90°,
∴四边形ABCM是矩形,
∴CM=AB=6,AM=BC=10,
在Rt△PCM中,PM8,
∴AP=AM﹣PM=2,
在Rt△PAE中,∵PE2=AP2+AE2,
∴x2=(6﹣x)2+22,
∴x,
∴BE.
(2)如图2中,以CE为直径作⊙,当⊙O与直线AD相切于点P时,存在唯一点P,使∠EPC=90°.连接OP,延长PO交BC于H.
∵AD是⊙O的切线,
∴OP⊥AD,
∴∠HPA=∠A=∠B=90°,
∴四边形PABH是矩形,
∴PH=AB=6,AP=BH,OH∥EB,
∵CO=OE,∴CH=HB=5,
∴OHEBa,AP=BH=5,
∵POEC,
∴6a ,
解得a,
∴AP=5,a.
21世纪教育网(www.21cnjy.com)
2025年九年级中考数学三轮冲刺训练隐圆训练
一、选择题
1.如图,在边长为2的等边△ABC中,点D、E分别是边BC、AC上两个动点,且满足
AE=CD,连接BE、AD相交于点P,则线段CP的最小值为( )
A.1 B.2 C. D.21
2.如图,⊙O的半径为1,弦AB=1,点P为优弧上一动点,AC⊥AP交直线PB于点C,则△ABC的最大面积是( )
A. B. C. D.
3.如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=2,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为( )
A.22 B. C. D.
4.如图,半径为2cm,圆心角为90°的扇形OAB的弧AB上有一运动的点P,从点P向半径OA引垂线PH交OA于点H.设△OPH的内心为I,当点P在弧AB上从点A运动到点B时,内心I所经过的路径长为( )
A.π B.π C.π D.π
5.直线y=x+4分别与x轴、y轴相交于点M,N,边长为2的正方形OABC一个顶点O在坐标系的原点,直线AN与MC相交于点P,若正方形绕着点O旋转一周,则点P到点(0,2)长度的最小值是( )
A.22 B.3﹣2 C. D.1
6.如图,在矩形ABCD中,AB=8,BC=6,点P在矩形的内部,连接PA,PB,PC,若∠PBC=∠PAB,则PC的最小值是( )
A.6 B.3 C.24 D.44
7.如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( )
A. B.2 C. D.
二、填空题
8.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是 .
9.如图,以G(0,1)为圆心,半径为2的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为⊙G上一动点,CF⊥AE于F.若点E从在圆周上运动一周,则点F所经过的路径长为 .
10.如图,点C是⊙O上一动点,弦AB=6,∠ACB=120°.△ABC内切圆半径r的最大值为 .
11.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
12.如图,AB是半⊙O的直径,点C在半⊙O上,AB=5cm,AC=4cm.D是上的一个动点,连接AD,过点C作CE⊥AD于E,连接BE.在点D移动的过程中,BE的最小值为 .
13.如图,点O是等边三角形ABC内的一点,连接OA、OB、OC,且∠AOB=135°,若AB=2,则OC的最小值为 .
14.如图,在等边△ABC中,AB=6,点D,E分别在边BC,AC上,且BD=CE,连接AD,BE交于点F,连接CF,则∠AFB= ,CF的最小值是 .
15.如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为 .
16.如图,在锐角三角形ABC中,BC=8,sinA,BN⊥AC于点N,CM⊥AB于点M,连接MN,则△AMN面积的最大值是 .
17.在△ABC中,AB=4,∠C=45°,则AC+BC的最大值为 .
三、解答题
18.如图,已知抛物线y=ax2x+4的对称轴是直线x=3,且与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C.
(1)求抛物线的解析式;
(2)以BC为边作正方形CBDE,求对角线BE所在直线的解析式;
(3)点P是抛物线上一点,若∠APB=45°,求出点P的坐标.
19.如图,在四边形ABCD中,∠B=60°,∠D=30°,AB=BC.
(1)求∠A+∠C的度数;
(2)连接BD,探究AD,BD,CD三者之间的数量关系,并说明理由;
(3)若AB=1,点E在四边形ABCD内部运动,且满足AE2=BE2+CE2,求点E运动路径的长度.
20.如图,在梯形ABCD中,AD∥BC,∠A=90°,AB=6,BC=10,AD=7,点P在边AD上运动(不与点A,D重合),E是边AB上一点,连接PC,PE,EC.
(1)当点B,P关于直线EC对称时,求BE的长;
(2)设BE=a,若存在唯一点P,使∠EPC=90°,求a,AP的值.
参考答案
一、选择题
1.【解答】解:∵CD=AE,BC=AC,
∴BD=CE,
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
∵∠APE=∠ABE+∠BAD,∠APE=∠BPD,∠ABE+∠CBE=60°,
∴∠BPD=∠APE=∠ABC=60°,
∴∠APB=120°,
∴点P的运动轨迹是,∠AOB=120°,连接CO,
∵OA=OB,CA=CB,OC=OC,
∴△AOC≌△BOC(SSS),
∴∠OAC=∠OBC,∠ACO=∠BCO=30°,
∵∠AOB+∠ACB=180°,
∴∠OAC+∠OBC=180°,
∴∠OAC=∠OBC=90°,
∴OC=AC÷cos30°=4,OAOC=2,
∴OP=2,
∵PC≥OC﹣OP,
∴PC≥2,
∴PC的最小值为2.
故选:B.
2.【解答】解:连接OA、OB,如图1,
∵OA=OB=1,AB=1,
∴△OAB为等边三角形,
∴∠AOB=60°,
∴∠APB∠AOB=30°,
∵AC⊥AP,
∴∠C=60°,
∵AB=1,要使△ABC的面积最大,则点C到AB的距离最大,
∵∠ACB=60°,点C在⊙D上,
∴∠ADB=120°,
如图2,作△ABC的外接圆D,
当点C在优弧AB的中点时,点C到AB的距离最大,此时△ABC为等边三角形,且面积为AB2,
∴△ABC的最大面积为.
故选:D.
3.【解答】解:连接AE,如图1,
∵∠BAC=90°,AB=AC,BC=2,
∴AB=AC=2,
∵AD为直径,
∴∠AED=90°,
∴∠AEB=90°,
∴点E在以AB为直径的⊙O上,
∵⊙O的半径为1,
连接OE,OC,
∴OEAB=1
在Rt△AOC中,
∵OA=1,AC=2,
∴OC,
由于OC,OE=1是定值,
点E在线段OC上时,CE最小,如图2,
∴CE=OC﹣OE1,
即线段CE长度的最小值为1.
故选:C.
4.【解答】解:如图,连OI,PI,AI,
∵△OPH的内心为I,
∴∠IOP=∠IOA,∠IPO=∠IPH,
∴∠PIO=180°﹣∠IPO﹣∠IOP=180°(∠HOP+∠OPH),
而PH⊥OA,即∠PHO=90°,
∴∠PIO=180°(∠HOP+∠OPH)=180°(180°﹣90°)=135°,
又∵OP=OA,OI公共,
而∠IOP=∠IOA,
∴△OPI≌△OAI,
∴∠AIO=∠PIO=135°,
所以点I在以OA为弦,并且所对的圆周角为135°的一段劣弧上;
过A、I、O三点作⊙O′,如图,连O′A,O′O,
在优弧AO取点P′,连P′A,P′O,
∵∠AIO=135°,
∴∠AP′O=180°﹣135°=45°,
∴∠AO′O=90°,而OA=2cm,
∴O′OOA2,
∴弧OA的长π(cm),
所以内心I所经过的路径长为 πcm.
故选:B.
5.【解答】解:在△MOC和△NOA中,
,
∴△MOC≌△NOA,
∴∠CMO=∠ANO,
∵∠CMO+∠MCO=90°,∠MCO=∠NCP,
∴∠NCP+∠CNP=90°,
∴∠MPN=90°
∴MP⊥NP,
在正方形旋转的过程中,同理可证,∴∠CMO=∠ANO,可得∠MPN=90°,MP⊥NP,
∴P在以MN为直径的圆上,
∵M(﹣4,0),N(0,4),
∴圆心G为(﹣2,2),半径为2,
∵PG﹣GC≤PC,
∴当圆心G,点P,C(0,2)三点共线时,PC最小,
∵GN=GM,CN=CO=2,
∴GCOM=2,
这个最小值为GP﹣GC=22.
故选:A.
6.【解答】解:∵四边形ABCD是矩形,
∴∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PBC=∠PAB,
∴∠PAB+∠PBA=90°,
∴∠APB=90°,
∴点P在以AB为直径的圆上运动,设圆心为O,连接OC交⊙O于P,此时PC最小,
∵OC2,
∴PC的最小值为24,
故选:C.
7.【解答】解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC,
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴OP=OA=OB(直角三角形斜边中线等于斜边一半),
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在Rt△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC5,
∴PC=OC﹣OP=5﹣3=2.
∴PC最小值为2.
故选:B.
二、填空题
8.【解答】解:在正方形ABCD中,AB=AD=CD,∠BAD=∠CDA,∠ADG=∠CDG,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴∠1=∠2,
在△ADG和△CDG中,
,
∴△ADG≌△CDG(SAS),
∴∠2=∠3,
∴∠1=∠3,
∵∠BAH+∠3=∠BAD=90°,
∴∠1+∠BAH=90°,
∴∠AHB=180°﹣90°=90°,
取AB的中点O,连接OH、OD,
则OH=AOAB=1,
在Rt△AOD中,OD,
根据三角形的三边关系,OH+DH>OD,
∴当O、D、H三点共线时,DH的长度最小,
最小值=OD﹣OH1.
(解法二:可以理解为点H是在Rt△AHB,AB直径的半圆上运动当O、H、D三点共线时,DH长度最小)
故答案为:1.
9.【解答】解:连接AG.
∵CF⊥AE于F,
∴AO,
在直角△AOC中,AC2,
则以AC为直径的圆的周长是2π.
故答案为:2π.
10.【解答】解:当点C为弧AB的中点时,△ABC内切圆半径r的最大,如图,连接OC交AB于D点,⊙M为△ABC的内切圆,作ME⊥AC于E点,
∵点C为弧AB的中点,
∴OC⊥AB,AD=BDAB=6,AC=BC,
∴点M在CD上,
∴ME和MD都为⊙M的半径,
设ME=MD=r,
∵∠ACB=120°,
∴∠A=30°,∠ACD=60°,
在Rt△ACD中,CDAD,
在Rt△CEM中,∠ECM=60°,∠CME=30°,
∴CEEMr,
∴CM=2CEr,
∵CM+DM=CD,
∴r+r,
∴r=6﹣3,
故答案为:6﹣3.
11.【解答】解:如图所示:∵MA′是定值,A′C长度取最小值时,即A′在MC上时,
过点M作MF⊥DC于点F,
∵在边长为2的菱形ABCD中,∠A=60°,M为AD中点,
∴2MD=AD=CD=2,∠FDM=60°,
∴∠FMD=30°,
∴FDMD,
∴FM=DM×cos30°,
∴MC,
∴A′C=MC﹣MA′1.
故答案为:1.
12.【解答】解:如图,取AC的中点为O',连接BO′、BC.
∵CE⊥AD,
∴∠AEC=90°,
∴在点D移动的过程中,点E在以AC为直径的圆上运动,
∵AB是直径,
∴∠ACB=90°,
在Rt△ABC中,∵AC=4cm,AB=5cm,
∴BC3cm,
在Rt△BCO′中,BO′cm,
∵O′E+BE≥O′B,
∴当O′、E、B共线时,BE的值最小,最小值为O′B﹣O′E2(cm),
故答案为:()cm.
13.【解答】解:如图,作△ABO的外接圆⊙G.连接AG,BG,OG,CG,CG交AB于J.
∵∠AOB=135°,
∴∠AGB=90°,
∵AB=2,
∴AG=GB=OG,
∵GA=GB,CA=CB,
∴CG垂直平分线段AB,
∴AJ=JB=1,
∴CJ,GJ=AJ=BJ=1,
∴CG=1,
∴OC≥CG﹣OG,
∴OC≥1,
∴OC的最小值为1.
故答案为:1.
14.【解答】解:如图,∵△ABC是等边三角形,
∴AB=BC=AC,∠ABC=∠BAC=∠BCE=60°,
∵BD=CE,
∴△ABD≌△BCE(SAS),
∴∠BAD=∠CBE,
又∵∠AFE=∠BAD+∠ABE,
∴∠AFE=∠CBE+∠ABE=∠ABC,
∴∠AFE=60°,
∴∠AFB=120°,
∴点F的运动轨迹是O为圆心,OA为半径的弧上运动(∠AOB=120°,OA=2),
连接OC交⊙O于N,当点F与N重合时,CF的值最小,最小值=OC﹣ON=422.
故答案为:120°,2.
15.【解答】解:∵CF⊥AE,
∴∠AFC=90°,
∴点F在以AC为直径的圆上运动,
以AC为直径画半圆AC,连接OA,
当点E与B重合时,此时点F与G重合,
当点E与D重合时,此时点F与A重合,
∴点E从点B出发顺时针运动到点D时,点F所经过的路径长为的长,
∵点G为OD的中点,
∴OGODOA=2,
∵OG⊥AB,
∴∠AOG=60°,AG=2,
∵OA=OC,
∴∠ACG=30°,
∴AC=2AG=4,
∴所在圆的半径为2,圆心角为60°,
∴的长为,
故答案为:.
16.【解答】解:画出△ABC的外接圆⊙O,连接OB,
∵BC=8,sinA,
∴点A在优弧BC上运动,
当A'O⊥BC时,△A'BC的面积最大,
∴BH=4,
∵∠BOH=∠BAC,
∴BO=5,OH=3,
∴AH=8,cos∠BOH,
∴S△ABC最大为32,
∵CM⊥AB,
∴cos∠MAC,
∵AB=AC,AM=AN,∠MAN=∠BAC,
∴△AMN∽△ABC,
∴,
∴,
∴S△AMN,
故答案为:.
17.【解答】解:过点B作BD⊥AC于点D,
∵∠C=45°,
∴△BCD为等腰直角三角形,
∴BD=CD,
设BD=CD=a,延长AC至点F,使得CF=a,
∵tan∠AFB,
作△ABF的外接圆⊙O,过点O作OE⊥AB于点E,则AEAB=2,∠AOE=∠AFB,
∴tan∠AOE,
∴OE=4,OA,
∴BC(ACBC)(AC+CF)(OA+OF),
∴BC的最大值为4.
故答案为:.
三、解答题
18.【解答】解:(1)∵抛物线的对称轴是直线x=3
∴3,解得:a
∴抛物线的解析式为yx2x+4
(2)当yx2x+4=0时,解得:x1=﹣2,x2=8
∴A(﹣2,0),B(8,0)
∴AB=10,OB=8
当x=0时,yx2x+4=4
∴C(0,4),OC=4
①如图1,若点E在第一象限,过点E作EF⊥y轴于点F
∴∠CFE=∠BOC=90°
∵四边形CBDE是正方形
∴∠BCE=90°,BC=CE
∴∠BCO+∠OBC=∠BCO+∠FCE=90°
∴∠OBC=∠FCE
在△FCE与△OBC中
∴△FCE≌△OBC(AAS)
∴FC=OB=8,EF=OC=4
∴OF=OC+FC=12
∴E(4,12)
设直线BE解析式为:y=kx+b
∴ 解得:
∴直线BE解析式为y=﹣3x+24
②如图2,若点E在第三象限,过点E作EF⊥y轴于点F
同理可证:△FCE≌△OBC(AAS)
∴FC=OB=8,EF=OC=4
∴OF=FC﹣OC=8﹣4=4
∴E(﹣4,﹣4)
设直线BE解析式为:y=k'x+b'
∴ 解得:
∴直线BE解析式为yx
综上所述,直线BE解析式为y=﹣3x+24 或yx
(3)以AB为斜边作等腰Rt△AGB,则AG=BG,∠AGB=90°
以点G为圆心、AG长为半径画圆,则点P在优弧AB上时总有∠APB=45°.
如图3,若点G在第一象限,⊙G与抛物线交点只有A、B,即没有满足条件的点P使∠APB=45°
如图4,若点G在第四象限,过点G作GM⊥x轴于点M
∴AM=BM=GMAB=5,
∴G(3,﹣5)
设P(p,p2p+4)
∵PG=AGAB=5,
∴PG2=50 可得方程:(p﹣3)2+(p2p+4+5)2=50,
∴(p﹣3)2[(p﹣3)2﹣45]2=50,
令p﹣3=t,
∴t2(t2﹣45)2=50,
解得t2=49或t2=25,
∴p1=﹣4,p2=10,p3=﹣2(即点A,舍去),p4=8(即点B,舍去)
∴p2p+4=﹣6
∴点P坐标为(﹣4,﹣6)或(10,﹣6)
19.【解答】解:(1)如图1中,
在四边形ABCD中,∵∠A+∠B+∠C+∠D=360°,∠B=60°,∠D=30°,
∴∠A+∠C=360°﹣60°﹣30°=270°.
(2)如图2中,结论:DB2=DA2+DC2.
理由:连接BD.以BD为边向下作等边三角形△BDQ.
∵∠ABC=∠DBQ=60°,
∴∠ABD=∠CBQ,
∵AB=BC,DB=BQ,
∴△ABD≌△CBQ(SAS),
∴AD=CQ,∠A=∠BCQ,
∵∠A+∠BCD=∠BCQ+∠BCD=270°,
∴∠DCQ=90°,
∴DQ2=DC2+CQ2,
∵CQ=DA,DQ=DB,
∴DB2=DA2+DC2.
(3)如图3中,连接AC,将△ACE绕点A顺时针旋转60°得到△ABR,连接RE.
则△AER是等边三角形,∵EA2=EB2+EC2,EA=RE,EC=RB,
∴RE2=RB2+EB2,
∴∠EBR=90°,
∴∠RAE+∠RBE=150°,
∴∠ARB+∠AEB=∠AEC+∠AEB=210°,
∴∠BEC=150°,
∴点E的运动轨迹在O为圆心的圆上,在⊙O上取一点K,连接KB,KC,OB,OC,
∵∠K+∠BEC=180°,
∴∠K=30°,∠BOC=60°,
∵OB=OC,
∴△OBC是等边三角形,
∴OB=OC=BC=1,
∴点E的运动路径.
20.【解答】解:(1)如图1中,作CM⊥AD于M.设BE=x.
∵△CEP是由△CEB翻折得到,
∴CP=CB=10,PE=EB=x,
∵∠A=90°,AD∥BC,
∴∠A=∠B=∠M=90°,
∴四边形ABCM是矩形,
∴CM=AB=6,AM=BC=10,
在Rt△PCM中,PM8,
∴AP=AM﹣PM=2,
在Rt△PAE中,∵PE2=AP2+AE2,
∴x2=(6﹣x)2+22,
∴x,
∴BE.
(2)如图2中,以CE为直径作⊙,当⊙O与直线AD相切于点P时,存在唯一点P,使∠EPC=90°.连接OP,延长PO交BC于H.
∵AD是⊙O的切线,
∴OP⊥AD,
∴∠HPA=∠A=∠B=90°,
∴四边形PABH是矩形,
∴PH=AB=6,AP=BH,OH∥EB,
∵CO=OE,∴CH=HB=5,
∴OHEBa,AP=BH=5,
∵POEC,
∴6a ,
解得a,
∴AP=5,a.
21世纪教育网(www.21cnjy.com)
同课章节目录
