2025年九年级数学中考三轮冲刺训练几何变换训练(含解析)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练几何变换训练(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 07:19:05 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练几何变换训练
1.在等腰直角△ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD.将线段AD绕点D按顺时针方向旋转90°得线段ED,连接BE.
【尝试发现】
(1)如图1,当点D在线段BC上时,线段BE与CD的数量关系为 ;
【类比探究】
(2)当点D在线段BC的延长线上时,先在图2中补全图形,再探究线段BE与CD的数量关系并证明;
【联系拓广】
(3)若AC=BC=1,CD=2,请直接写出sin∠ECD的值.
2.在△ABC中,AC=BC,∠ACB=120°,点D是AB上一个动点(点D不与A,B重合),以点D为中心,将线段DC顺时针旋转120°得到线DE.
(1)如图1,当∠ACD=15°时,求∠BDE的度数;
(2)如图2,连接BE,当0°<∠ACD<90°时,∠ABE的大小是否发生变化?如果不变,求∠ABE的度数;如果变化,请说明理由;
(3)如图3,点M在CD上,且CM:MD=3:2,以点C为中心,将线CM逆时针转120°得到线段CN,连接EN,若AC=4,求线段EN的取值范围.
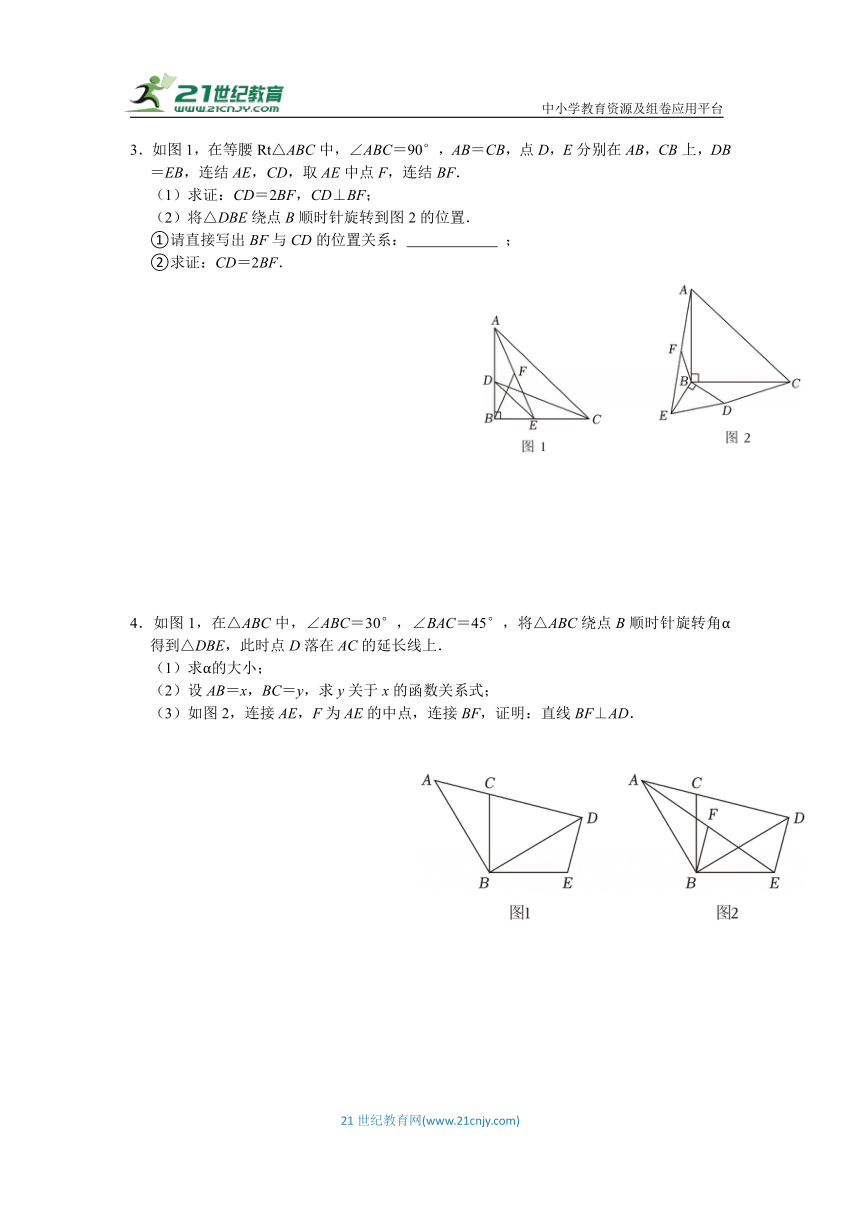
3.如图1,在等腰Rt△ABC中,∠ABC=90°,AB=CB,点D,E分别在AB,CB上,DB=EB,连结AE,CD,取AE中点F,连结BF.
(1)求证:CD=2BF,CD⊥BF;
(2)将△DBE绕点B顺时针旋转到图2的位置.
①请直接写出BF与CD的位置关系: ;
②求证:CD=2BF.
4.如图1,在△ABC中,∠ABC=30°,∠BAC=45°,将△ABC绕点B顺时针旋转角α得到△DBE,此时点D落在AC的延长线上.
(1)求α的大小;
(2)设AB=x,BC=y,求y关于x的函数关系式;
(3)如图2,连接AE,F为AE的中点,连接BF,证明:直线BF⊥AD.
5.如图,在△ABC中,∠ABC=90°,∠ACB=α(0°<α<45°).将线段CA绕点C顺时针旋转90°得到线段CD,过点D作DE⊥BC,垂足为E.
(1)如图1,求证:△ABC≌△CED.
(2)如图2,∠ACD的平分线与AB的延长线相交于点F,连接DF,DF的延长线与CB的延长线相交于点P,猜想PC与PD的数量关系,并加以证明.
(3)如图3,在(2)的条件下,将△BFP沿AF折叠,在α变化过程中,当点P落在点E的位置时,连接EF.
①求证:点F是PD的中点;
②若CD=20,求△CEF的面积.
6.在Rt△ABC中,∠ACB=90°,AC=BC,过点B作BD∥AC.
(1)如图1,若点D在点B的左侧,连接CD,过点A作AE⊥CD交BC于点E.若点E是BC的中点,求证:AC=2BD;
(2)如图2,若点D在点B的右侧,连接AD,点F是AD的中点,连接BF并延长交AC于点G,连接CF.过点F作FM⊥BG交AB于点M,CN平分∠ACB交BG于点N,求证:AM=CNBD;
(3)若点D在点B的右侧,连接AD,点F是AD的中点,且AF=AC.点P是直线AC上一动点,连接FP,将FP绕点F逆时针旋转60°得到FQ,连接BQ,点R是直线AD上一动点,连接BR,QR.在点P的运动过程中,当BQ取得最小值时,在平面内将△BQR沿直线QR翻折得到△TQR,连接FT.在点R的运动过程中,直接写出的最大值.
7.在Rt△ABC中,∠ACB=90°,AC=1,BC=3.
(1)问题发现
如图1,将△CAB绕点C按逆时针方向旋转90°得到△CDE,连接AD,BE,线段AD与BE的数量关系是 ,AD与BE的位置关系是 ;
(2)类比探究
将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,连接AD,BE,线段AD与BE的数量关系,位置关系与(1)中结论是否一致?若AD交CE于点N,请结合图2说明理由;
(3)迁移应用
如图3,将△CAB绕点C旋转一定角度得到△CDE,当点D落到AB边上时,连接BE,求线段BE的长.
8.【模型建立】
(1)如图1,△ABC和△BDE都是等边三角形,点C关于AD的对称点F在BD边上.
①求证:AE=CD;
②用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型应用】
(2)如图2,△ABC是直角三角形,AB=AC,CD⊥BD,垂足为D,点C关于AD的对称点F在BD边上.用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型迁移】
(3)在(2)的条件下,若AD=4,BD=3CD,求cos∠AFB的值.
9.在Rt△ABC中,∠ACB=90°,CA=CB,点O为AB的中点,点D在直线AB上(不与点A,B重合),连接CD,线段CD绕点C逆时针旋转90°,得到线段CE,过点B作直线l⊥BC,过点E作EF⊥l,垂足为点F,直线EF交直线OC于点G.
(1)如图1,当点D与点O重合时,请直接写出线段AD与线段EF的数量关系;
(2)如图2,当点D在线段AB上时,求证:CG+BDBC;
(3)连接DE,△CDE的面积记为S1,△ABC的面积记为S2,当EF:BC=1:3时,请直接写出的值.
10.在Rt△ABC中,M是斜边AB的中点,将线段MA绕点M旋转至MD位置,点D在直线AB外,连接AD,BD.
(1)如图1,求∠ADB的大小;
(2)已知点D和边AC上的点E满足ME⊥AD,DE∥AB.
(i)如图2,连接CD,求证:BD=CD;
(ii)如图3,连接BE,若AC=8,BC=6,求tan∠ABE的值.
11.如图,在等边△ABC中,AD⊥BC于点D,E为线段AD上一动点(不与A,D重合),连接BE,CE,将CE绕点C顺时针旋转60°得到线段CF,连接AF.
(1)如图1,求证:∠CBE=∠CAF;
(2)如图2,连接BF交AC于点G,连接DG,EF,EF与DG所在直线交于点H,求证:EH=FH;
(3)如图3,连接BF交AC于点G,连接DG,EG,将△AEG沿AG所在直线翻折至△ABC所在平面内,得到△APG,将△DEG沿DG所在直线翻折至△ABC所在平面内,得到△DQG,连接PQ,QF.若AB=4,直接写出PQ+QF的最小值.
12.如图1,已知线段AB,AC,线段AC绕点A在直线AB上方旋转,连接BC,以BC为边在BC上方作Rt△BDC,且∠DBC=30°.
(1)若∠BDC=90°,以AB为边在AB上方作Rt△BAE,且∠AEB=90°,∠EBA=30°,连接DE,用等式表示线段AC与DE的数量关系是 ;
(2)如图2,在(1)的条件下,若DE⊥AB,AB=4,AC=2,求BC的长;
(3)如图3,若∠BCD=90°,AB=4,AC=2,当AD的值最大时,求此时tan∠CBA的值.
13.如图,在Rt△ABC中,,点D在AB边上,连接CD,将CD绕点C逆时针旋转90°得到CE,连接BE,DE.
(1)求证:△CAD≌△CBE;
(2)若AD=2时,求CE的长;
(3)点D在AB上运动时,试探究AD2+BD2的值是否存在最小值,如果存在,求出这个最小值;如果不存在,请说明理由.
14.如图,四边形ABCD是正方形,点M在BC上,点N在CD的延长线上,BM=DN,连接AM,AN,点H在BC的延长线上,∠MAH=2∠BAM,点E在线段BH上,且HE=AM,将线段EH绕点E逆时针旋转得到线段EG,使得∠HEG=∠MAH,EG交AH于点F.
(1)线段AM与线段AN的关系是 .
(2)若EF=5,FG=4,求AH的长.
(3)求证:FH=2BM.
15.在△ABC中,∠BAC=90°,AB=AC,线段AB绕点A逆时针旋转至AD(AD不与AC重合),旋转角记为α,∠DAC的平分线AE与射线BD相交于点E,连接EC.
(1)如图①,当α=20°时,∠AEB的度数是 ;
(2)如图②,当0°<α<90°时,求证:BD+2CEAE;
(3)当0°<α<180°,AE=2CE时,请直接写出的值.
16.如图,在△ABC中,AB=AC,∠BAC=120°,点D在直线AC上,连接BD,将DB绕点D逆时针旋转120°,得到线段DE,连接BE,CE.
(1)求证:BCAB;
(2)当点D在线段AC上(点D不与点A,C重合)时,求的值;
(3)过点A作AN∥DE交BD于点N,若AD=2CD,请直接写出的值.
17.如图,在Rt△ABC中,点P为斜边BC上一动点,将△ABP沿直线AP折叠,使得点B的对应点为B′,连接AB′,CB′,BB′,PB′.
(1)如图①,若PB′⊥AC,证明:PB′=AB′.
(2)如图②,若AB=AC,BP=3PC,求cos∠B′AC的值.
(3)如图③,若∠ACB=30°,是否存在点P,使得AB=CB′.若存在,求此时的值;若不存在,请说明理由.
参考答案
1.【解答】解:(1)如图,过点E作EM⊥CB延长线于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴BM=DM﹣BD=AC﹣BD=BC﹣BD=CD,
∴BM=EM,
∵EM⊥CB,
∴,
故答案为:;
(2)补全图形如图,,理由如下:
过点E作EM⊥BC于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴DM=BC,
∴DM﹣CM=BC﹣CM,
∴CD=BM,
∴EM=BM,
∵EM⊥CB,
∴;
(3)如图,当点D在CB延长线上时,过点E作EM⊥CB延长线于点M,
由(2)得DM=AC=1,EM=CD=2,
∴CM=CD+DM=3,
∴,
∴;
当点D在BC延长线上时,过点E作EM⊥CB于点M,
同理可得:△ACD≌△DME,
∴DM=AC=1,ME=CD=2,
∴CM=2﹣1=1,
∴CE,
∴sin∠ECD,
综上,sin∠ECD或.
2.【解答】解:(1)∵AC=BC,
∴∠A=∠B,
∴∠BDC=∠A+∠ACD=30°+15°=45°,
∵线段DC顺时针旋转120°得到线DE,
∴∠CDE=120°,
∴∠BDE=∠CDE﹣∠BDC=120°﹣45°=75°;
(2)方法一,
如图1,
∠ABE的度数不变,理由如下:
连接CE,
∵线段DC顺时针旋转120°得到线DE,
∴∠CDE=120°,CD=DE,
∴∠DCE=∠DEC=30°,
∵AC=BC,∠ACB=120°,
∴∠ABC=∠A=30°,
∴∠DEC=∠ABC,
∴点B、C、D、E共圆,
∴∠ABE=∠DCE=30°,
方法二,
如图1,
连接CE,
由上知:∠DEC=∠ABC,
∵∠DOE=∠BOC,
∴△DOE∽△COB,
∴,
∵∠COD=∠BOE,
∴△COD∽△BOE,
∴∠ABE=∠DCE=30°;
(3)如图2,
连接CE,
由(2)知,
∠DCE=30°,
∵线段CM时针转120°得到线段CN,
∴∠DCN=120°,CN=CM,
∴∠ECN=∠DCN﹣∠DCE=120°﹣30°=90°,
设CN=CM=3a,DM=2a,DE=CD=5a,
∴CECD=5,
∴EN2a,
∵点D在AB上,
∴AC≤CD<AC,
∴2≤5a<4,
∴a,
∴EN.
3.【解答】(1)证明:在△ABE和△CBD中,
∵AB=BC,∠ABE=∠CBD,BE=BD,
∴△ABE≌△CBD(SAS),
∴AE=CD,∠FAB=∠BCD.
∵F是Rt△ABE斜边AE的中点,
∴AE=2BF,
∴CD=2BF,
∵,
∴∠FAB=∠FBA.
∴∠FBA=∠BCD,
∵∠FBA+∠FBC=90°,
∴∠FBC+∠BCD=90°.
∴BF⊥CD;
(2)①BF⊥CD;
理由如下:延长BF到点G,使FG=BF,连结AG.延长EB到M,使BE=BM,连接AM并延长交CD于点N.
证△AGB≌△BDC(具体证法过程跟②一样).
∴∠ABG=∠BCD,
∵F是AE中点,B是EM中点,
∴BF是△ABM中位线,
∴BF∥AN,
∴∠ABG=∠BAN=∠BCD,
∴∠ABC=∠ANC=90°,
∴AN⊥CD,
∵BF∥AN,
∴BF⊥CD.
故答案为:BF⊥CD;
②证明:延长BF到点G,使FG=BF,连结AG.
∵AF=EF,FG=BF,∠AFG=∠EFB,
∴△AGF≌△EBF(SAS),
∴∠FAG=∠FEB,AG=BE.
∴AG∥BE.
∴∠GAB+∠ABE=180°,
∵∠ABC=∠EBD=90°,
∴∠ABE+∠DBC=180°,
∴∠GAB=∠DBC.
∵BE=BD,
∴AG=BD.
在△AGB和△BDC中,
∵AG=BD,∠GAB=∠DBC,AB=CB,
∴△AGB≌△BDC(SAS),
∴CD=BG.
∵BG=2BF,
∴CD=2BF,
4.【解答】解:(1)由旋转可得BA=BD,
又∵点D落在AC的延长线上,∠BAC=45°,
∴∠BDA=∠BAC=45°,
∴α=∠ABD=90°,
(2)如图1,过点C作CG⊥AB于点G,
∵∠BAC=45°,则△ACG是等腰直角三角形,
∴AG=CG,
∵∠ABC=30°,AB=x,BC=y,
∴,,
∵,
∴,
(3)证明:如图2,连接DF,
∵∠BDA=∠A=45°,由旋转可得∠BDE=∠BAC=45°,
∴∠DAE=90°,
∴DE⊥AD,
∵F是AE的中点,
∴DF=AF,
在△ABF和△DBF中,
,
∴△ABF≌△DBF(SSS),
∴,
∴∠FBD=∠BDE=45°,
∴BF∥DE,
∴BF⊥AD.
5.【解答】(1)证明:∵DE⊥BC,
∴∠DEC=90°,
∴∠D+∠DCE=90°,
∵∠ABC=90°,
∴∠ABC=∠DEC,
∵线段CA绕点C顺时针旋转90°得到线段CD,
∴∠ACD=90°,AC=CD,
∴∠DCE+∠ACB=90°,
∴∠ACB=∠D,
∴△ABC≌△CED(AAS);
(2)PC=PD,理由如下:
∵CF是∠ACD的平分线,
∴∠ACF=∠DCF,
由(1)知,
AC=CD,△ABC≌△CED,
∴∠A=∠DCE,
∵CF=CF,
∴△ACF≌△DCF(SAS),
∴∠A=∠PDC,
∴∠PDC=∠DCE,
∴PC=PD;
(3)①∵△BFP沿AF折叠,点P落在点E,
∴PF=EF,∠P=∠PEF,
∵DE⊥BC,
∴∠PED=90°,
∴∠PEF+∠DEF=90°,∠P+∠PDE=90°,
∴∠PEF+∠PDE=90°,
∴∠PDE=∠DEF,
∴EF=DF,
∴PF=DF,
∴点F是PD的中点;
②解:设CE=a,BC=DE=b,
∴BE=BC﹣CE=b﹣a,
由①知,
点F是PD的中点,
∴PFPD,
∵∠ABC=∠PED=90°,
∴BF∥DE,
∴△PBF∽△PED,
∴,
∴PE=2BE=2(b﹣a),BFDEb,
∴S△CEF,
∵∠PED=90°,DE=b,PE=2(b﹣a),PD=PC=PE+CE=2(b﹣a)+a=2b﹣a,
∴b2+[2(b﹣a)]2=(2b﹣a)2,
化简得,
3a2﹣4ab+b2=0,
∴b=a或b=3a,
∵0°<α<45°,
∴a=b舍去,
∴b=3a,
∴S△CEF,
∵∠DEC=90°,
∴a2+b2=202,
∴a2+(3a)2=400,
∴a2=40,
∴S△CEF,
∴△CEF的面积是30.
6.【解答】证明:(1)∵∠ACB=90°,BD∥AC,
∴∠CBD=180°﹣∠ACB=90°,
∵AE⊥CD,
∴∠ACD+∠CAE=90°,
∵∠ACD+∠BCD=90°,
∴∠CAE=∠BCD,
又∵AC=CB,∠CBD=∠ACE=90°,
∴△ACE≌△CBD(ASA),
∴BD=CE,
∵点E是BC的中点,
∴BC=2CE=2BD,
∴AC=2BD;
证明:(2)过点G作GH⊥AB于H,连接HF,
∵BD∥AC,
∴∠FBD=∠FGA,∠D=∠FAG,
∵点F是AD的中点,
∴AF=DF,
∴△AGF≌△DBF(AAS),
∴AG=BD,BF=GF,
∵AC=BC,∠ACB=90°,
∴∠CAB=∠ACB=45°,
∵GH⊥AH,
∴△AHG是等腰直角三角形,
∴,
∵∠BHG=∠BCG=90°,BF=GF,
∴,
∴∠FBH=∠FHB,∠FBC=∠FCB,
∴∠GFH=∠FBH+∠FHB=2∠FBH,∠GFC=∠FBC+∠FCB=2∠FBC,
∴∠HFC=∠GFH+∠GFC=2∠FBH+2∠FBC=2∠ABC=90°,
∵FM⊥BG,
∴∠BFM=90°,
∴∠HFM=∠CFN,
设∠CBG=x,则∠ABG=45°﹣x,∠CGB=90°﹣x,
∴∠HMF=∠BFM+∠FBM=135°﹣x,
∵CN平分∠ACB,
∴,
∴∠CNF=∠CGN+∠GCN=135°﹣x,
∴∠HMF=∠CNF,
∴△HFM≌△CFN(AAS),
∴HM=CN,
∵AM=AH+HM,
∴;
(3)解:过点D作DH⊥AC交AC延长线与H,连接FH,
∵BD∥AC,∠ACB=90°,
∴∠BCH=∠CBD=90°,
∵DH⊥AC,
∴四边形BCHD是矩形,
∴BC=DH=AC,
∵点F是AD的中点,且AF=AC,
∴AD=2AF=2DH=2FH=2DF,
∴△FDH是等边三角形,
∴∠DFH=∠FDH=60°,
∴∠BDA=∠DAH=30°,
∴∠FHA=∠FAH=30°,
由旋转的性质可得FQ=FP,∠PFQ=60°=∠DFH,
∴∠DFQ=∠HFP,
∴△DFQ≌△HFP(SAS),
∴∠FDQ=∠FHP=30°,
∴点Q在直线DQ上运动,
设直线DQ交FH于K,则DK⊥FH,,,
∴∠BDQ=60°,
由垂线段最短可知,当BQ⊥DQ时,BQ有最小值,
∴∠DBQ=30°,
设AC=DH=6a,则,
∴,
∴,
∴,
在Rt△DFK中,,
∴,
∴QK=DK﹣DQ=3a,
在Rt△FQK中,由勾股定理得,
∵△DFQ≌△HFP,
∴,
∴,
∴由折叠的性质可得:,
∵FT≤FQ+TQ,
∴,
∴当点Q在线段FT上时,此时有最大值,最大值为,
∴的最大值为.
7.【解答】解:(1)如图1,延长DA交BE于H,
∵将△CAB绕点C按逆时针方向旋转90°得到△CDE,
∴AC=DC=1,BC=CE=3,∠ECB=∠ACD=90°,
∴AD,BE=3,∠CAD=∠ADC=45°,∠CBE=∠CEB=45°,
∴BE=3AD,∠CAD=∠EAH=45°,
∴∠EHA=90°,
∴AD⊥BE,
故答案为:BE=3AD,AD⊥BE;
(2)线段AD与BE的数量关系,位置关系与(1)中结论一致,理由如下:
如图2,延长DA交BE于H,
∵将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,
∴AC=DC=1,BC=CE=3,∠ECB=∠ACD,
∴,
∴△BCE∽△ACD,
∴,∠CDA=∠CEB,
∴BE=3AD,
∵∠CEB+∠ENH=∠CDA+∠CND=90°,
∴∠EHD=90°,
∴AD⊥BE;
(3)如图3,过点C作CN⊥AB于N,
∵∠ACB=90°,AC=1,BC=3,
∴AB,
∵CN⊥AB,
∴∠ANC=90°=∠ACB,
又∵∠A=∠A,
∴△ACN∽△ABC,
∴,
∴AN 1,
∴AN,
∵AC=DC,CN⊥AB,
∴AD=2AN,
由(2)可知:BE=3AD.
8.【解答】(1)证明:①∵△ABC和△BDE都是等边三角形,
∴AB=CB,EB=DB,∠ABC=∠EBD=60°,
∴∠ABE=∠CBD,
∴△ABE≌△CBD,
∴AE=CD;
②解:AD=BD+DF.
理由如下:
∵△BDE是等边三角形,
∴BD=DE,
∵点C与点F关于AD对称,
∴CD=DF,
∵AD=AE+DE,
∴AD=BD+DF;
(2)BD+DFAD.
理由如下:
如图1,过点B作BE⊥AD于E,
∵点C与点F关于AD对称,
∴∠ADC=∠ADB,
又∵CD⊥BD,
∴∠ADC=∠ADB=45°,
又∵BE⊥AD,
∴△BDE是等腰直角三角形,
又∵△ABC是等腰直角三角形,
∴,∠ABC=∠EBD=45°,
∴∠ABE=∠CBD,
∴△ABE∽△CBD,
∴,CD=DF,
∴DFAE,
∵△BDE是等腰直角三角形,
∴BD,
∴BD+DF,
即:BD+DFAD.
(3)解:如图2,过点A作AG⊥BD于G,
又∵∠ADB=45°,
∴△AGD是等腰直角三角形,
又∵AD=4,
∴AG=DG=4,BD+DFAD=8,
∵BD=3CD,CD=DF,
∴DF=2,
又∵DG=4,
∴FG=DG﹣DF=2,
在Rt△AFG中,由勾股定理得:,
∴cos∠AFB.
9.【解答】(1)解:ADEF,理由如下:
连接BE,如图:
∵∠ACB=90°,CA=CB,
∴∠A=45°,
∵线段CD绕点C逆时针旋转90°,得到线段CE,
∴CD=CE,∠DCE=90°,
∴∠BCE=90°﹣∠BCD=∠ACD,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠A=∠CBE=45°,
∵直线l⊥BC,
∴∠EBF=45°,
∴△BEF是等腰直角三角形,
∴BEEF,
∴ADEF;
(2)证明:如图,
∵∠ACB=90°,CA=CB,O为AB的中点,
∴∠COB=90°,ABBC,
∵∠BFG=90°,
∴∠G=360°﹣∠COB﹣∠OBF﹣∠BFG=45°=∠A,
∵BC⊥直线l,EF⊥直线l,
∴BC∥GF,
∴∠CEG=∠BCE,
∵∠BCE=90°﹣∠BCD=∠ACD,
∴∠CEG=∠ACD,
∵CE=CD,
∴△CEG≌△DCA(AAS),
∴CG=AD,
∵AD+BD=AB,
∴CG+BDBC;
(3)解:由EF:BC=1:3,设EF=m,则BC=AC=3m,
当D在线段AB上时,延长AC交GF于K,如图:
由(2)知△CEG≌△DCA,
∴GE=AC=3m,
∵∠CBF=∠BFE=∠BCK=90°,
∴四边形BCKF是矩形,
∴KF=BC=3m,∠CKG=90°,
∴KE=KF﹣EF=2m,
∴GK=GE﹣KE=m,
∵∠G=45°,
∴CK=GK=m,
∴CE2=CK2+KE2=m2+(2m)2=5m2,
∴S1CD CECE2,
∵AC=BC=3m,
∴S2AC BC,
∴;
当D在射线BA上时,延长EG交AC于T,如图:
同理可得BC=AC=EG=3m,
∴FG=EG﹣EF=2m,
∵TF=BC=3m,
∴TG=TF﹣FG=m,
∵∠ACB=90°,CA=CB,O为AB的中点,
∴∠AOC=45°,
∵BC∥EF,
∴∠ETC=90°,
∴CT=TG=m,
∴CE2=CT2+TE2=m2+(m+3m)2=17m2,
∴S1,
∴;
综上所述,的值为或.
10.【解答】(1)解:∵M是AB的中点,
∴MA=MB,
由旋转的性质得:MA=MD=MB,
∴∠MAD=∠MDA,∠MDB=∠MBD,
∵∠MAD+∠MDA+∠MDB+∠MBD=180°,
∴∠ADB=∠MDA+∠MDB=90°,
即∠ADB的大小为90°;
(2)(i)证明:∵∠ADB=90°,
∴AD⊥BD,
∵ME⊥AD,
∴ME∥BD,
∵ED∥BM,
∴四边形EMBD是平行四边形,
∴DE=BM=AM,
∴DE∥AM,
∴四边形EAMD是平行四边形,
∵EM⊥AD,
∴平行四边形EAMD是菱形,
∴∠BAD=∠CAD,
又∵∠ACB=∠ADB=90°,
∴A、C、D、B四点共圆,
∵∠BCD=∠CAD,
∴,
∴BD=CD;
(ii)解:如图3,过点E作EH⊥AB于点H,
则∠EHA=∠EHB=90°,
在Rt△ABC中,由勾股定理得:AB10,
∵四边形EAMD是菱形,
∴AE=AMAB=5,
∴sin∠CAB,
∴EH=AE sin∠CAB=53,
∴AH4,
∴BH=AB﹣AH=10﹣4=6,
∴tan∠ABE,
即tan∠ABE的值为.
11.【解答】(1)证明:∵△ABC为等边三角形,
∴∠ACB=60°,AC=BC,
∵将CE绕点C顺时针旋转60°得到线段CF,
∴CE=CF,∠ECF=60°,
∵△ABC是等边三角形,
∴∠BCA=∠ECF,
∴∠BCE=∠ACF,
∴△BCE≌△ACF(SAS),
∴∠CBE=∠CAF;
(2)证明:如图所示,过点F作FK∥AD,交DH点的延长线于点K,连接EK,FD,
∵△ABC是等边三角形,
∴AB=AC=BC,
∵AD⊥BC,
∴BD=CD,
∴AD垂直平分BC,
∴EB=EC,
又∵△BCE≌△ACF,
∴AF=BE,CF=CE,
∴AF=CF,
∴F在AC的垂直平分线上,
∵AB=BC,
∴B在AC的垂直平分线上,
∴BF垂直平分AC,
∴AC⊥BF,AG=CGAC,
∴∠AGF=90°,
又∵DGAC=CG,∠ACD=60°,
∴△DCG是等边三角形,
∴∠CGD=∠CDG=60°,
∴∠AGH=∠DGC=60°,
∴∠KGF=∠AGF﹣∠AGH=90°﹣60°=30°,
又∵∠ADK=∠ADC﹣∠GDC=90°﹣60=30°,KF∥AD,
∴∠HKF=∠ADK=30°,
∴∠FKG=∠KGF=30°,
∴FG=FK,
在Rt△CED与Rt△CGF中,
,
∴Rt△CED≌Rt△CFG,
∴GF=ED,
∴ED=FK,
∴四边形EDFK是平行四边形,
∴EH=HF;
解法二:连接CH,证明∠CHE=90°,可得结论.
(3)解:依题意,如图所示,延长AP,DQ交于点R,
由(2)可知△DCG是等边三角形,
∴∠EDG=30°,
∵将△AEG沿AG所在直线翻折至△ABC所在平面内,得到△APG,将△DEG沿DG所在直线翻折至△ABC所在平面内,得到△DQG,
∴∠PAG=∠EAG=30°,∠QDG=∠EDG=30°,
∴∠PAE=∠QDE=60°,
∴△ADR是等边三角形,
∴∠QDC=∠ADC﹣∠ADQ=90°﹣60°=30°,
由(2)可得Rt△CED≌Rt△CFG,
∴DE=GF,
∴DE=DQ,
∴GF=DQ,
∵∠GBC=∠QDC=30°,
∴GF∥DQ,
∴四边形GDQF是平行四边形,
∴QF=DGAC=2,
由(2)可知G是AC的中点,则GA=GD,
∴∠GAD=∠GDA=30°,
∴∠AGD=120°,
∵折叠,
∴∠AGP+∠DGQ=∠AGE+∠DGE=∠AGD=120°,
∴∠PGQ=360°﹣2∠AGD=120°,
又PG=GE=GQ,
∴PQPGGQ,
∴当GQ取得最小值时,即GQ⊥DR时,PQ取得最小值,此时如图所示,
∴GQGCDC=1,
∴PQ,
∴PQ+QF2.
解法二:由两次翻折,推得∠PGQ=360°﹣240°=120°,则PQPGEG,
由QF=DG=2,推出PQ1+QF的最小值,只需要求出EG的最小值,
当EG⊥AD时,EG的值最小,最小值为1,
∴PQ+QF的最小值为2.
12.【解答】解:(1)在Rt△BDC中,∠DBC=30°,在Rt△BAE中,∠AEB=90°,∠EBA=30°,
∴△ABE∽△CBD,∠DBE+∠EBC=∠ABC+∠EBC,,
∴,∠DBE=∠CBA,
∴△ABC∽△EBD,
∴,
∴,
故答案为:ACDE;
(2)在Rt△BAE,∠AEB=90°,∠EBA=30°,AB=4,
∴AE=AB sin∠EBAAB=2,∠BAE=60°,
延长DE交AB于点F,如图所示,
∴,,
∴BF=AB﹣AF=4﹣1=3,
由(1)可得,
∴,
∴,
在Rt△BFD中,,
∵△ABC∽△EBD,
∴,
∴,
即;
(3)如图所示,以AB为边在AB上方作Rt△BAE,且∠EAB=90°,∠EBA=30°,连接BE,EA,ED,EC,
同(1)可得△BDE∽△BCA,
∴,
∵AC=2,
∴,
在Rt△AEB中,AB=4,,
∴D在以E为圆心,为半径的圆上运动,
∴当点A,E,D三点共线时,AD的值最大,此时如图所示,则,
在Rt△ABD中,,
∴cos∠BDA,sin∠BDA,
∵∠BEA=60°,
∴∠BED=120°,
∵△ABC∽△EBD,
∴∠BDE=∠BCA,
过点A作AF⊥BC于点F,
∴,,
∵∠DBC=30°,
∴BCBD2,
∴,
Rt△AFB中,tan.
13.【解答】(1)证明:由题意,可知∠ACB=∠DCE=90°,CA=CB,CD=CE.
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB.
即∠ACD=∠BCE.
在△CAD和△CBE中,
∴△CAD≌△CBE(SAS);
(2)解:∵在 Rt△ABC中,,
∴∠CAB=∠CBA=45°,,
∴BD=AB﹣AD=6﹣2=4.
∵△CAD≌△CBE(SAS),
∴BE=AD=2,∠CBE=∠CAD=45°,
∴∠ABE=∠ABC+∠CBE=90°.
∴,
∴在 Rt△CDE 中,;
(3)解:存在,理由:
由(2)可知,AD2+BD2=BE2+BD2=DE2=2CD2,
∴当CD最小时,有 AD2+BD2 的值最小,此时 CD⊥AB.
∵△ABC 为等腰直角三角形,
∴,
∴AD2+BD2=2CD2≥2×32=18.
即 AD2+BD2 的最小值为18.
14.【解答】(1)解:∵四边形ABCD是正方形,
∴∠ADN=∠ADC=∠B=90°,AD=AB,
∵BM=DN,
∴△ADN≌△ABM(SAS),
∴BM=CN,∠DAN=∠BAM,
∴∠DAN+∠DAM=∠BAM+∠DAM=∠BAD=90°,
∴∠MAN=90°,
∴AM⊥AN,
故答案为:垂直且相等;
(2)解:∵∠H=∠H,∠HEG=∠MAH,
∴△HEF∽△HAM,
∴,
∵线段EH绕点E逆时针旋转得到线段EG,
∴EH=EG=EF+FG=9,
∴AM=HE=9,
∴,
∴AH;
(3)证明:如图,
延长MB至X,使BX=BM,作∠AMR=∠H,交AX于R,
∴XM=2BM,
∵AB⊥XM,
∴AX=AM,
∴∠XAB=∠BAM,∠X=∠AMB,
设∠XAB=∠BAM=α,
∴∠MAH=∠XAM=∠HEF=2α,∠X=∠AMB=90°﹣α,
∴∠AMR=∠H=90°﹣∠BAH=90°﹣3α,
∴∠MRX=∠XAM+∠AMR=2α+(90°﹣3α)=90°﹣α,
∴∠X=∠MRX,
∴RM=XM,
∵∠XAM=∠HEF=2α,∠AMR=∠H,EH=AM,
∴△HEF≌△MAR(ASA),
∴FH=RM=XM=2BM.
15.【解答】(1)解:∵线段AB绕点A逆时针旋转α至AD,α=20°,
∴∠BAD=20°,AB=AD,
∴∠ADB=∠ABD(180°﹣20°)=80°,
又∵∠BAC=90°,
∴∠DAC=70°,
∵AE平分∠DAC,
∴∠DAE∠DAC=35°,
∴∠AEB=∠ADB﹣∠DAE=80°﹣35°=45°,
故答案为:45°;
(2)证明:延长DB到F,使BF=CE,连接AF,
∵AB=AC,AD=AB,
∴AD=AC,
∵AE平分∠DAC,
∴∠DAE=∠CAE,
又∵AE=AE,
∴△ADE≌△ACE(SAS),
∴∠DEA=∠CEA,∠ADE=∠ACE,DE=CE,
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ADE+∠ADB=180°,
∴∠ACE+∠ABD=180°,
∵∠BAC=90°,
∴∠BEC=360°﹣(∠ACE+∠ABD)﹣∠BAC=360°﹣180°﹣90°=90°,
∵∠DEA=∠CEA,
∴∠DEA=∠CEA90°=45°,
∵∠ABF+∠ABD=180°,∠ACE+∠ABD=180°,
∴∠ABF=∠ACE,
∵AB=AC,BF=CE,
∴△ABF≌△ACE(SAS),
∴AF=AE,∠AFB=∠AEC=45°,
∴∠FAE=180°﹣45°﹣45°=90°,
在Rt△AFE中,∠FAE=90°,
∵cos∠AEF,
∴EF,
∵EF=BF+BD+DE=CE+BD+CE=BD+2CE,
∴BD+2CEAE;
(3)解:如图3,当0°<α<90°时,
由(2)可知BD+2CEAE,CE=DE,
∵AE=2CE,
∴BD+2DE=2DE,
∴2;
如图4,当90°<α<180°时,
在BD上截取BF=DE,连接AF,方法同(2)可证△ADE≌△ACE(SAS),
∴DE=CE,
∵AB=AC=AD,
∴∠ABF=∠ADE,
∴△ABF≌△ADE(SAS),
∴AF=AE,∠BAF=∠DAE,
又∵∠DAE=∠CAE,
∴∠BAF=∠CAE,
∴∠EAF=∠FAC+∠CAE=∠FAC+∠BAF=∠BAC=90°,
∴△AEF是等腰直角三角形,
∴EFAE,
∴BD=BF+DE+EF=2DEAE,
∵AE=2CE=2DE,
∴BD=2DE+2DE,
∴2.
综上所述,的值为22或22.
16.【解答】(1)证明:如图1,
作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH60°,BC=2BH,
∴sin60°,
∴BH,
∴BC=2BH;
(2)解:∵AB=AC,
∴∠ABC=∠ACB30°,
由(1)得,
,
同理可得,
∠DBE=30°,,
∴∠ABC=∠DBE,,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
∴∠ABD=∠CBE,
∴△ABD∽△CBE,
∴;
(3)解:如图2,
当点D在线段AC上时,
作BF⊥AC,交CA的延长线于F,作AG⊥BD于G,
设AB=AC=3a,则AD=2a,
由(1)得,CE,
在Rt△ABF中,∠BAF=180°﹣∠BAC=60°,AB=3a,
∴AF=3a cos60°,BF=3a.sin60°,
在Rt△BDF中,DF=AD+AF=2aa,
BDa,
∵∠AGD=∠F=90°,∠ADG=∠BDF,
∴△DAG∽△DBF,
∴,
∴,
∴AG,
∵AN∥DE,
∴∠AND=∠BDE=120°,
∴∠ANG=60°,
∴ANaa,
∴,
如图3,
当点D在AC的延长线上时,
设AB=AC=2a,则AD=4a,
由(1)得,
CE4,
作BR⊥CA,交CA的延长线于R,作AQ⊥BD于Q,
同理可得,
AR=a,BR,
∴BD2a,
∴,
∴AQ,
∴ANa,
∴,
综上所述:或.
17.【解答】解:(1)证明:∵PB'⊥AC,∠CAB=90°,
∴PB'∥AB.
∴∠B'PA=∠BAP,
又由折叠可知∠BAP=∠B'AP,
∴∠B'PA=∠B'AP.
故PB′=AB′.
(2)设AB=AC=a,AC、PB'交于点D,如答图1所示,
则△ABC为等腰直角三角形,
∴BC,PC,PB,
由折叠可知,∠PB'A=∠B=45°,
又∠ACB=45°,
∴∠PB'A=∠ACB,
又∠CDP=∠B'DA,
∴△CDP∽△B'DA.
∴.①
设B'D=b,则CDb.
∴AD=AC﹣CD=ab,
PD=PB'﹣B'D=PB﹣B'Db,
由①得:.
解得:b.
过点D作DE⊥AB'于点E,则△B'DE为等腰直角三角形.
∴B'E=sin45°×B'D,
∴AE=AB'﹣B'E=AB﹣B'E=a.
又AD=AC﹣CD=ab=a.
∴cos∠B'AC=cos∠EAD.
(3)存在点P,使得CB'=AB=m.理由如下:
∵∠ACB=30°,∠CAB=90°.
∴BC=2m.
①如答图2所示,
由题意可知,点B'的运动轨迹为以A为圆心、AB为半径的半圆A.
当P为BC中点时,PC=BP=AP=AB'=m,
又∠B=60°,
∴△PAB为等边三角形.
又由折叠可得四边形ABPB'为菱形.
∴PB'∥AB,
∴PB'⊥AC.
又∵AP=AB',
则易知AC为PB'的垂直平分线.
故CB'=PC=AB=m,满足题意.
此时,.
②当点B'落在BC上时,如答图3所示,
此时CB'=AB=m,
则PB',
∴PC=CB'+PB'=m,
∴.
综上所述,的值为或.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练几何变换训练
1.在等腰直角△ABC中,∠ACB=90°,AC=BC,D为直线BC上任意一点,连接AD.将线段AD绕点D按顺时针方向旋转90°得线段ED,连接BE.
【尝试发现】
(1)如图1,当点D在线段BC上时,线段BE与CD的数量关系为 ;
【类比探究】
(2)当点D在线段BC的延长线上时,先在图2中补全图形,再探究线段BE与CD的数量关系并证明;
【联系拓广】
(3)若AC=BC=1,CD=2,请直接写出sin∠ECD的值.
2.在△ABC中,AC=BC,∠ACB=120°,点D是AB上一个动点(点D不与A,B重合),以点D为中心,将线段DC顺时针旋转120°得到线DE.
(1)如图1,当∠ACD=15°时,求∠BDE的度数;
(2)如图2,连接BE,当0°<∠ACD<90°时,∠ABE的大小是否发生变化?如果不变,求∠ABE的度数;如果变化,请说明理由;
(3)如图3,点M在CD上,且CM:MD=3:2,以点C为中心,将线CM逆时针转120°得到线段CN,连接EN,若AC=4,求线段EN的取值范围.
3.如图1,在等腰Rt△ABC中,∠ABC=90°,AB=CB,点D,E分别在AB,CB上,DB=EB,连结AE,CD,取AE中点F,连结BF.
(1)求证:CD=2BF,CD⊥BF;
(2)将△DBE绕点B顺时针旋转到图2的位置.
①请直接写出BF与CD的位置关系: ;
②求证:CD=2BF.
4.如图1,在△ABC中,∠ABC=30°,∠BAC=45°,将△ABC绕点B顺时针旋转角α得到△DBE,此时点D落在AC的延长线上.
(1)求α的大小;
(2)设AB=x,BC=y,求y关于x的函数关系式;
(3)如图2,连接AE,F为AE的中点,连接BF,证明:直线BF⊥AD.
5.如图,在△ABC中,∠ABC=90°,∠ACB=α(0°<α<45°).将线段CA绕点C顺时针旋转90°得到线段CD,过点D作DE⊥BC,垂足为E.
(1)如图1,求证:△ABC≌△CED.
(2)如图2,∠ACD的平分线与AB的延长线相交于点F,连接DF,DF的延长线与CB的延长线相交于点P,猜想PC与PD的数量关系,并加以证明.
(3)如图3,在(2)的条件下,将△BFP沿AF折叠,在α变化过程中,当点P落在点E的位置时,连接EF.
①求证:点F是PD的中点;
②若CD=20,求△CEF的面积.
6.在Rt△ABC中,∠ACB=90°,AC=BC,过点B作BD∥AC.
(1)如图1,若点D在点B的左侧,连接CD,过点A作AE⊥CD交BC于点E.若点E是BC的中点,求证:AC=2BD;
(2)如图2,若点D在点B的右侧,连接AD,点F是AD的中点,连接BF并延长交AC于点G,连接CF.过点F作FM⊥BG交AB于点M,CN平分∠ACB交BG于点N,求证:AM=CNBD;
(3)若点D在点B的右侧,连接AD,点F是AD的中点,且AF=AC.点P是直线AC上一动点,连接FP,将FP绕点F逆时针旋转60°得到FQ,连接BQ,点R是直线AD上一动点,连接BR,QR.在点P的运动过程中,当BQ取得最小值时,在平面内将△BQR沿直线QR翻折得到△TQR,连接FT.在点R的运动过程中,直接写出的最大值.
7.在Rt△ABC中,∠ACB=90°,AC=1,BC=3.
(1)问题发现
如图1,将△CAB绕点C按逆时针方向旋转90°得到△CDE,连接AD,BE,线段AD与BE的数量关系是 ,AD与BE的位置关系是 ;
(2)类比探究
将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,连接AD,BE,线段AD与BE的数量关系,位置关系与(1)中结论是否一致?若AD交CE于点N,请结合图2说明理由;
(3)迁移应用
如图3,将△CAB绕点C旋转一定角度得到△CDE,当点D落到AB边上时,连接BE,求线段BE的长.
8.【模型建立】
(1)如图1,△ABC和△BDE都是等边三角形,点C关于AD的对称点F在BD边上.
①求证:AE=CD;
②用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型应用】
(2)如图2,△ABC是直角三角形,AB=AC,CD⊥BD,垂足为D,点C关于AD的对称点F在BD边上.用等式写出线段AD,BD,DF的数量关系,并说明理由;
【模型迁移】
(3)在(2)的条件下,若AD=4,BD=3CD,求cos∠AFB的值.
9.在Rt△ABC中,∠ACB=90°,CA=CB,点O为AB的中点,点D在直线AB上(不与点A,B重合),连接CD,线段CD绕点C逆时针旋转90°,得到线段CE,过点B作直线l⊥BC,过点E作EF⊥l,垂足为点F,直线EF交直线OC于点G.
(1)如图1,当点D与点O重合时,请直接写出线段AD与线段EF的数量关系;
(2)如图2,当点D在线段AB上时,求证:CG+BDBC;
(3)连接DE,△CDE的面积记为S1,△ABC的面积记为S2,当EF:BC=1:3时,请直接写出的值.
10.在Rt△ABC中,M是斜边AB的中点,将线段MA绕点M旋转至MD位置,点D在直线AB外,连接AD,BD.
(1)如图1,求∠ADB的大小;
(2)已知点D和边AC上的点E满足ME⊥AD,DE∥AB.
(i)如图2,连接CD,求证:BD=CD;
(ii)如图3,连接BE,若AC=8,BC=6,求tan∠ABE的值.
11.如图,在等边△ABC中,AD⊥BC于点D,E为线段AD上一动点(不与A,D重合),连接BE,CE,将CE绕点C顺时针旋转60°得到线段CF,连接AF.
(1)如图1,求证:∠CBE=∠CAF;
(2)如图2,连接BF交AC于点G,连接DG,EF,EF与DG所在直线交于点H,求证:EH=FH;
(3)如图3,连接BF交AC于点G,连接DG,EG,将△AEG沿AG所在直线翻折至△ABC所在平面内,得到△APG,将△DEG沿DG所在直线翻折至△ABC所在平面内,得到△DQG,连接PQ,QF.若AB=4,直接写出PQ+QF的最小值.
12.如图1,已知线段AB,AC,线段AC绕点A在直线AB上方旋转,连接BC,以BC为边在BC上方作Rt△BDC,且∠DBC=30°.
(1)若∠BDC=90°,以AB为边在AB上方作Rt△BAE,且∠AEB=90°,∠EBA=30°,连接DE,用等式表示线段AC与DE的数量关系是 ;
(2)如图2,在(1)的条件下,若DE⊥AB,AB=4,AC=2,求BC的长;
(3)如图3,若∠BCD=90°,AB=4,AC=2,当AD的值最大时,求此时tan∠CBA的值.
13.如图,在Rt△ABC中,,点D在AB边上,连接CD,将CD绕点C逆时针旋转90°得到CE,连接BE,DE.
(1)求证:△CAD≌△CBE;
(2)若AD=2时,求CE的长;
(3)点D在AB上运动时,试探究AD2+BD2的值是否存在最小值,如果存在,求出这个最小值;如果不存在,请说明理由.
14.如图,四边形ABCD是正方形,点M在BC上,点N在CD的延长线上,BM=DN,连接AM,AN,点H在BC的延长线上,∠MAH=2∠BAM,点E在线段BH上,且HE=AM,将线段EH绕点E逆时针旋转得到线段EG,使得∠HEG=∠MAH,EG交AH于点F.
(1)线段AM与线段AN的关系是 .
(2)若EF=5,FG=4,求AH的长.
(3)求证:FH=2BM.
15.在△ABC中,∠BAC=90°,AB=AC,线段AB绕点A逆时针旋转至AD(AD不与AC重合),旋转角记为α,∠DAC的平分线AE与射线BD相交于点E,连接EC.
(1)如图①,当α=20°时,∠AEB的度数是 ;
(2)如图②,当0°<α<90°时,求证:BD+2CEAE;
(3)当0°<α<180°,AE=2CE时,请直接写出的值.
16.如图,在△ABC中,AB=AC,∠BAC=120°,点D在直线AC上,连接BD,将DB绕点D逆时针旋转120°,得到线段DE,连接BE,CE.
(1)求证:BCAB;
(2)当点D在线段AC上(点D不与点A,C重合)时,求的值;
(3)过点A作AN∥DE交BD于点N,若AD=2CD,请直接写出的值.
17.如图,在Rt△ABC中,点P为斜边BC上一动点,将△ABP沿直线AP折叠,使得点B的对应点为B′,连接AB′,CB′,BB′,PB′.
(1)如图①,若PB′⊥AC,证明:PB′=AB′.
(2)如图②,若AB=AC,BP=3PC,求cos∠B′AC的值.
(3)如图③,若∠ACB=30°,是否存在点P,使得AB=CB′.若存在,求此时的值;若不存在,请说明理由.
参考答案
1.【解答】解:(1)如图,过点E作EM⊥CB延长线于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴BM=DM﹣BD=AC﹣BD=BC﹣BD=CD,
∴BM=EM,
∵EM⊥CB,
∴,
故答案为:;
(2)补全图形如图,,理由如下:
过点E作EM⊥BC于点M,
由旋转得AD=DE,∠ADE=90°,
∴∠ADC+∠EDM=90°,
∵∠ACB=90°,
∴∠ACD=∠DME,∠ADC+∠CAD=90°,
∴∠CAD=∠EDM,
∴△ACD≌△DME(AAS),
∴CD=EM,AC=DM,
∵AC=BC,
∴DM=BC,
∴DM﹣CM=BC﹣CM,
∴CD=BM,
∴EM=BM,
∵EM⊥CB,
∴;
(3)如图,当点D在CB延长线上时,过点E作EM⊥CB延长线于点M,
由(2)得DM=AC=1,EM=CD=2,
∴CM=CD+DM=3,
∴,
∴;
当点D在BC延长线上时,过点E作EM⊥CB于点M,
同理可得:△ACD≌△DME,
∴DM=AC=1,ME=CD=2,
∴CM=2﹣1=1,
∴CE,
∴sin∠ECD,
综上,sin∠ECD或.
2.【解答】解:(1)∵AC=BC,
∴∠A=∠B,
∴∠BDC=∠A+∠ACD=30°+15°=45°,
∵线段DC顺时针旋转120°得到线DE,
∴∠CDE=120°,
∴∠BDE=∠CDE﹣∠BDC=120°﹣45°=75°;
(2)方法一,
如图1,
∠ABE的度数不变,理由如下:
连接CE,
∵线段DC顺时针旋转120°得到线DE,
∴∠CDE=120°,CD=DE,
∴∠DCE=∠DEC=30°,
∵AC=BC,∠ACB=120°,
∴∠ABC=∠A=30°,
∴∠DEC=∠ABC,
∴点B、C、D、E共圆,
∴∠ABE=∠DCE=30°,
方法二,
如图1,
连接CE,
由上知:∠DEC=∠ABC,
∵∠DOE=∠BOC,
∴△DOE∽△COB,
∴,
∵∠COD=∠BOE,
∴△COD∽△BOE,
∴∠ABE=∠DCE=30°;
(3)如图2,
连接CE,
由(2)知,
∠DCE=30°,
∵线段CM时针转120°得到线段CN,
∴∠DCN=120°,CN=CM,
∴∠ECN=∠DCN﹣∠DCE=120°﹣30°=90°,
设CN=CM=3a,DM=2a,DE=CD=5a,
∴CECD=5,
∴EN2a,
∵点D在AB上,
∴AC≤CD<AC,
∴2≤5a<4,
∴a,
∴EN.
3.【解答】(1)证明:在△ABE和△CBD中,
∵AB=BC,∠ABE=∠CBD,BE=BD,
∴△ABE≌△CBD(SAS),
∴AE=CD,∠FAB=∠BCD.
∵F是Rt△ABE斜边AE的中点,
∴AE=2BF,
∴CD=2BF,
∵,
∴∠FAB=∠FBA.
∴∠FBA=∠BCD,
∵∠FBA+∠FBC=90°,
∴∠FBC+∠BCD=90°.
∴BF⊥CD;
(2)①BF⊥CD;
理由如下:延长BF到点G,使FG=BF,连结AG.延长EB到M,使BE=BM,连接AM并延长交CD于点N.
证△AGB≌△BDC(具体证法过程跟②一样).
∴∠ABG=∠BCD,
∵F是AE中点,B是EM中点,
∴BF是△ABM中位线,
∴BF∥AN,
∴∠ABG=∠BAN=∠BCD,
∴∠ABC=∠ANC=90°,
∴AN⊥CD,
∵BF∥AN,
∴BF⊥CD.
故答案为:BF⊥CD;
②证明:延长BF到点G,使FG=BF,连结AG.
∵AF=EF,FG=BF,∠AFG=∠EFB,
∴△AGF≌△EBF(SAS),
∴∠FAG=∠FEB,AG=BE.
∴AG∥BE.
∴∠GAB+∠ABE=180°,
∵∠ABC=∠EBD=90°,
∴∠ABE+∠DBC=180°,
∴∠GAB=∠DBC.
∵BE=BD,
∴AG=BD.
在△AGB和△BDC中,
∵AG=BD,∠GAB=∠DBC,AB=CB,
∴△AGB≌△BDC(SAS),
∴CD=BG.
∵BG=2BF,
∴CD=2BF,
4.【解答】解:(1)由旋转可得BA=BD,
又∵点D落在AC的延长线上,∠BAC=45°,
∴∠BDA=∠BAC=45°,
∴α=∠ABD=90°,
(2)如图1,过点C作CG⊥AB于点G,
∵∠BAC=45°,则△ACG是等腰直角三角形,
∴AG=CG,
∵∠ABC=30°,AB=x,BC=y,
∴,,
∵,
∴,
(3)证明:如图2,连接DF,
∵∠BDA=∠A=45°,由旋转可得∠BDE=∠BAC=45°,
∴∠DAE=90°,
∴DE⊥AD,
∵F是AE的中点,
∴DF=AF,
在△ABF和△DBF中,
,
∴△ABF≌△DBF(SSS),
∴,
∴∠FBD=∠BDE=45°,
∴BF∥DE,
∴BF⊥AD.
5.【解答】(1)证明:∵DE⊥BC,
∴∠DEC=90°,
∴∠D+∠DCE=90°,
∵∠ABC=90°,
∴∠ABC=∠DEC,
∵线段CA绕点C顺时针旋转90°得到线段CD,
∴∠ACD=90°,AC=CD,
∴∠DCE+∠ACB=90°,
∴∠ACB=∠D,
∴△ABC≌△CED(AAS);
(2)PC=PD,理由如下:
∵CF是∠ACD的平分线,
∴∠ACF=∠DCF,
由(1)知,
AC=CD,△ABC≌△CED,
∴∠A=∠DCE,
∵CF=CF,
∴△ACF≌△DCF(SAS),
∴∠A=∠PDC,
∴∠PDC=∠DCE,
∴PC=PD;
(3)①∵△BFP沿AF折叠,点P落在点E,
∴PF=EF,∠P=∠PEF,
∵DE⊥BC,
∴∠PED=90°,
∴∠PEF+∠DEF=90°,∠P+∠PDE=90°,
∴∠PEF+∠PDE=90°,
∴∠PDE=∠DEF,
∴EF=DF,
∴PF=DF,
∴点F是PD的中点;
②解:设CE=a,BC=DE=b,
∴BE=BC﹣CE=b﹣a,
由①知,
点F是PD的中点,
∴PFPD,
∵∠ABC=∠PED=90°,
∴BF∥DE,
∴△PBF∽△PED,
∴,
∴PE=2BE=2(b﹣a),BFDEb,
∴S△CEF,
∵∠PED=90°,DE=b,PE=2(b﹣a),PD=PC=PE+CE=2(b﹣a)+a=2b﹣a,
∴b2+[2(b﹣a)]2=(2b﹣a)2,
化简得,
3a2﹣4ab+b2=0,
∴b=a或b=3a,
∵0°<α<45°,
∴a=b舍去,
∴b=3a,
∴S△CEF,
∵∠DEC=90°,
∴a2+b2=202,
∴a2+(3a)2=400,
∴a2=40,
∴S△CEF,
∴△CEF的面积是30.
6.【解答】证明:(1)∵∠ACB=90°,BD∥AC,
∴∠CBD=180°﹣∠ACB=90°,
∵AE⊥CD,
∴∠ACD+∠CAE=90°,
∵∠ACD+∠BCD=90°,
∴∠CAE=∠BCD,
又∵AC=CB,∠CBD=∠ACE=90°,
∴△ACE≌△CBD(ASA),
∴BD=CE,
∵点E是BC的中点,
∴BC=2CE=2BD,
∴AC=2BD;
证明:(2)过点G作GH⊥AB于H,连接HF,
∵BD∥AC,
∴∠FBD=∠FGA,∠D=∠FAG,
∵点F是AD的中点,
∴AF=DF,
∴△AGF≌△DBF(AAS),
∴AG=BD,BF=GF,
∵AC=BC,∠ACB=90°,
∴∠CAB=∠ACB=45°,
∵GH⊥AH,
∴△AHG是等腰直角三角形,
∴,
∵∠BHG=∠BCG=90°,BF=GF,
∴,
∴∠FBH=∠FHB,∠FBC=∠FCB,
∴∠GFH=∠FBH+∠FHB=2∠FBH,∠GFC=∠FBC+∠FCB=2∠FBC,
∴∠HFC=∠GFH+∠GFC=2∠FBH+2∠FBC=2∠ABC=90°,
∵FM⊥BG,
∴∠BFM=90°,
∴∠HFM=∠CFN,
设∠CBG=x,则∠ABG=45°﹣x,∠CGB=90°﹣x,
∴∠HMF=∠BFM+∠FBM=135°﹣x,
∵CN平分∠ACB,
∴,
∴∠CNF=∠CGN+∠GCN=135°﹣x,
∴∠HMF=∠CNF,
∴△HFM≌△CFN(AAS),
∴HM=CN,
∵AM=AH+HM,
∴;
(3)解:过点D作DH⊥AC交AC延长线与H,连接FH,
∵BD∥AC,∠ACB=90°,
∴∠BCH=∠CBD=90°,
∵DH⊥AC,
∴四边形BCHD是矩形,
∴BC=DH=AC,
∵点F是AD的中点,且AF=AC,
∴AD=2AF=2DH=2FH=2DF,
∴△FDH是等边三角形,
∴∠DFH=∠FDH=60°,
∴∠BDA=∠DAH=30°,
∴∠FHA=∠FAH=30°,
由旋转的性质可得FQ=FP,∠PFQ=60°=∠DFH,
∴∠DFQ=∠HFP,
∴△DFQ≌△HFP(SAS),
∴∠FDQ=∠FHP=30°,
∴点Q在直线DQ上运动,
设直线DQ交FH于K,则DK⊥FH,,,
∴∠BDQ=60°,
由垂线段最短可知,当BQ⊥DQ时,BQ有最小值,
∴∠DBQ=30°,
设AC=DH=6a,则,
∴,
∴,
∴,
在Rt△DFK中,,
∴,
∴QK=DK﹣DQ=3a,
在Rt△FQK中,由勾股定理得,
∵△DFQ≌△HFP,
∴,
∴,
∴由折叠的性质可得:,
∵FT≤FQ+TQ,
∴,
∴当点Q在线段FT上时,此时有最大值,最大值为,
∴的最大值为.
7.【解答】解:(1)如图1,延长DA交BE于H,
∵将△CAB绕点C按逆时针方向旋转90°得到△CDE,
∴AC=DC=1,BC=CE=3,∠ECB=∠ACD=90°,
∴AD,BE=3,∠CAD=∠ADC=45°,∠CBE=∠CEB=45°,
∴BE=3AD,∠CAD=∠EAH=45°,
∴∠EHA=90°,
∴AD⊥BE,
故答案为:BE=3AD,AD⊥BE;
(2)线段AD与BE的数量关系,位置关系与(1)中结论一致,理由如下:
如图2,延长DA交BE于H,
∵将△CAB绕点C按逆时针方向旋转任意角度得到△CDE,
∴AC=DC=1,BC=CE=3,∠ECB=∠ACD,
∴,
∴△BCE∽△ACD,
∴,∠CDA=∠CEB,
∴BE=3AD,
∵∠CEB+∠ENH=∠CDA+∠CND=90°,
∴∠EHD=90°,
∴AD⊥BE;
(3)如图3,过点C作CN⊥AB于N,
∵∠ACB=90°,AC=1,BC=3,
∴AB,
∵CN⊥AB,
∴∠ANC=90°=∠ACB,
又∵∠A=∠A,
∴△ACN∽△ABC,
∴,
∴AN 1,
∴AN,
∵AC=DC,CN⊥AB,
∴AD=2AN,
由(2)可知:BE=3AD.
8.【解答】(1)证明:①∵△ABC和△BDE都是等边三角形,
∴AB=CB,EB=DB,∠ABC=∠EBD=60°,
∴∠ABE=∠CBD,
∴△ABE≌△CBD,
∴AE=CD;
②解:AD=BD+DF.
理由如下:
∵△BDE是等边三角形,
∴BD=DE,
∵点C与点F关于AD对称,
∴CD=DF,
∵AD=AE+DE,
∴AD=BD+DF;
(2)BD+DFAD.
理由如下:
如图1,过点B作BE⊥AD于E,
∵点C与点F关于AD对称,
∴∠ADC=∠ADB,
又∵CD⊥BD,
∴∠ADC=∠ADB=45°,
又∵BE⊥AD,
∴△BDE是等腰直角三角形,
又∵△ABC是等腰直角三角形,
∴,∠ABC=∠EBD=45°,
∴∠ABE=∠CBD,
∴△ABE∽△CBD,
∴,CD=DF,
∴DFAE,
∵△BDE是等腰直角三角形,
∴BD,
∴BD+DF,
即:BD+DFAD.
(3)解:如图2,过点A作AG⊥BD于G,
又∵∠ADB=45°,
∴△AGD是等腰直角三角形,
又∵AD=4,
∴AG=DG=4,BD+DFAD=8,
∵BD=3CD,CD=DF,
∴DF=2,
又∵DG=4,
∴FG=DG﹣DF=2,
在Rt△AFG中,由勾股定理得:,
∴cos∠AFB.
9.【解答】(1)解:ADEF,理由如下:
连接BE,如图:
∵∠ACB=90°,CA=CB,
∴∠A=45°,
∵线段CD绕点C逆时针旋转90°,得到线段CE,
∴CD=CE,∠DCE=90°,
∴∠BCE=90°﹣∠BCD=∠ACD,
∴△BCE≌△ACD(SAS),
∴BE=AD,∠A=∠CBE=45°,
∵直线l⊥BC,
∴∠EBF=45°,
∴△BEF是等腰直角三角形,
∴BEEF,
∴ADEF;
(2)证明:如图,
∵∠ACB=90°,CA=CB,O为AB的中点,
∴∠COB=90°,ABBC,
∵∠BFG=90°,
∴∠G=360°﹣∠COB﹣∠OBF﹣∠BFG=45°=∠A,
∵BC⊥直线l,EF⊥直线l,
∴BC∥GF,
∴∠CEG=∠BCE,
∵∠BCE=90°﹣∠BCD=∠ACD,
∴∠CEG=∠ACD,
∵CE=CD,
∴△CEG≌△DCA(AAS),
∴CG=AD,
∵AD+BD=AB,
∴CG+BDBC;
(3)解:由EF:BC=1:3,设EF=m,则BC=AC=3m,
当D在线段AB上时,延长AC交GF于K,如图:
由(2)知△CEG≌△DCA,
∴GE=AC=3m,
∵∠CBF=∠BFE=∠BCK=90°,
∴四边形BCKF是矩形,
∴KF=BC=3m,∠CKG=90°,
∴KE=KF﹣EF=2m,
∴GK=GE﹣KE=m,
∵∠G=45°,
∴CK=GK=m,
∴CE2=CK2+KE2=m2+(2m)2=5m2,
∴S1CD CECE2,
∵AC=BC=3m,
∴S2AC BC,
∴;
当D在射线BA上时,延长EG交AC于T,如图:
同理可得BC=AC=EG=3m,
∴FG=EG﹣EF=2m,
∵TF=BC=3m,
∴TG=TF﹣FG=m,
∵∠ACB=90°,CA=CB,O为AB的中点,
∴∠AOC=45°,
∵BC∥EF,
∴∠ETC=90°,
∴CT=TG=m,
∴CE2=CT2+TE2=m2+(m+3m)2=17m2,
∴S1,
∴;
综上所述,的值为或.
10.【解答】(1)解:∵M是AB的中点,
∴MA=MB,
由旋转的性质得:MA=MD=MB,
∴∠MAD=∠MDA,∠MDB=∠MBD,
∵∠MAD+∠MDA+∠MDB+∠MBD=180°,
∴∠ADB=∠MDA+∠MDB=90°,
即∠ADB的大小为90°;
(2)(i)证明:∵∠ADB=90°,
∴AD⊥BD,
∵ME⊥AD,
∴ME∥BD,
∵ED∥BM,
∴四边形EMBD是平行四边形,
∴DE=BM=AM,
∴DE∥AM,
∴四边形EAMD是平行四边形,
∵EM⊥AD,
∴平行四边形EAMD是菱形,
∴∠BAD=∠CAD,
又∵∠ACB=∠ADB=90°,
∴A、C、D、B四点共圆,
∵∠BCD=∠CAD,
∴,
∴BD=CD;
(ii)解:如图3,过点E作EH⊥AB于点H,
则∠EHA=∠EHB=90°,
在Rt△ABC中,由勾股定理得:AB10,
∵四边形EAMD是菱形,
∴AE=AMAB=5,
∴sin∠CAB,
∴EH=AE sin∠CAB=53,
∴AH4,
∴BH=AB﹣AH=10﹣4=6,
∴tan∠ABE,
即tan∠ABE的值为.
11.【解答】(1)证明:∵△ABC为等边三角形,
∴∠ACB=60°,AC=BC,
∵将CE绕点C顺时针旋转60°得到线段CF,
∴CE=CF,∠ECF=60°,
∵△ABC是等边三角形,
∴∠BCA=∠ECF,
∴∠BCE=∠ACF,
∴△BCE≌△ACF(SAS),
∴∠CBE=∠CAF;
(2)证明:如图所示,过点F作FK∥AD,交DH点的延长线于点K,连接EK,FD,
∵△ABC是等边三角形,
∴AB=AC=BC,
∵AD⊥BC,
∴BD=CD,
∴AD垂直平分BC,
∴EB=EC,
又∵△BCE≌△ACF,
∴AF=BE,CF=CE,
∴AF=CF,
∴F在AC的垂直平分线上,
∵AB=BC,
∴B在AC的垂直平分线上,
∴BF垂直平分AC,
∴AC⊥BF,AG=CGAC,
∴∠AGF=90°,
又∵DGAC=CG,∠ACD=60°,
∴△DCG是等边三角形,
∴∠CGD=∠CDG=60°,
∴∠AGH=∠DGC=60°,
∴∠KGF=∠AGF﹣∠AGH=90°﹣60°=30°,
又∵∠ADK=∠ADC﹣∠GDC=90°﹣60=30°,KF∥AD,
∴∠HKF=∠ADK=30°,
∴∠FKG=∠KGF=30°,
∴FG=FK,
在Rt△CED与Rt△CGF中,
,
∴Rt△CED≌Rt△CFG,
∴GF=ED,
∴ED=FK,
∴四边形EDFK是平行四边形,
∴EH=HF;
解法二:连接CH,证明∠CHE=90°,可得结论.
(3)解:依题意,如图所示,延长AP,DQ交于点R,
由(2)可知△DCG是等边三角形,
∴∠EDG=30°,
∵将△AEG沿AG所在直线翻折至△ABC所在平面内,得到△APG,将△DEG沿DG所在直线翻折至△ABC所在平面内,得到△DQG,
∴∠PAG=∠EAG=30°,∠QDG=∠EDG=30°,
∴∠PAE=∠QDE=60°,
∴△ADR是等边三角形,
∴∠QDC=∠ADC﹣∠ADQ=90°﹣60°=30°,
由(2)可得Rt△CED≌Rt△CFG,
∴DE=GF,
∴DE=DQ,
∴GF=DQ,
∵∠GBC=∠QDC=30°,
∴GF∥DQ,
∴四边形GDQF是平行四边形,
∴QF=DGAC=2,
由(2)可知G是AC的中点,则GA=GD,
∴∠GAD=∠GDA=30°,
∴∠AGD=120°,
∵折叠,
∴∠AGP+∠DGQ=∠AGE+∠DGE=∠AGD=120°,
∴∠PGQ=360°﹣2∠AGD=120°,
又PG=GE=GQ,
∴PQPGGQ,
∴当GQ取得最小值时,即GQ⊥DR时,PQ取得最小值,此时如图所示,
∴GQGCDC=1,
∴PQ,
∴PQ+QF2.
解法二:由两次翻折,推得∠PGQ=360°﹣240°=120°,则PQPGEG,
由QF=DG=2,推出PQ1+QF的最小值,只需要求出EG的最小值,
当EG⊥AD时,EG的值最小,最小值为1,
∴PQ+QF的最小值为2.
12.【解答】解:(1)在Rt△BDC中,∠DBC=30°,在Rt△BAE中,∠AEB=90°,∠EBA=30°,
∴△ABE∽△CBD,∠DBE+∠EBC=∠ABC+∠EBC,,
∴,∠DBE=∠CBA,
∴△ABC∽△EBD,
∴,
∴,
故答案为:ACDE;
(2)在Rt△BAE,∠AEB=90°,∠EBA=30°,AB=4,
∴AE=AB sin∠EBAAB=2,∠BAE=60°,
延长DE交AB于点F,如图所示,
∴,,
∴BF=AB﹣AF=4﹣1=3,
由(1)可得,
∴,
∴,
在Rt△BFD中,,
∵△ABC∽△EBD,
∴,
∴,
即;
(3)如图所示,以AB为边在AB上方作Rt△BAE,且∠EAB=90°,∠EBA=30°,连接BE,EA,ED,EC,
同(1)可得△BDE∽△BCA,
∴,
∵AC=2,
∴,
在Rt△AEB中,AB=4,,
∴D在以E为圆心,为半径的圆上运动,
∴当点A,E,D三点共线时,AD的值最大,此时如图所示,则,
在Rt△ABD中,,
∴cos∠BDA,sin∠BDA,
∵∠BEA=60°,
∴∠BED=120°,
∵△ABC∽△EBD,
∴∠BDE=∠BCA,
过点A作AF⊥BC于点F,
∴,,
∵∠DBC=30°,
∴BCBD2,
∴,
Rt△AFB中,tan.
13.【解答】(1)证明:由题意,可知∠ACB=∠DCE=90°,CA=CB,CD=CE.
∴∠ACB﹣∠DCB=∠DCE﹣∠DCB.
即∠ACD=∠BCE.
在△CAD和△CBE中,
∴△CAD≌△CBE(SAS);
(2)解:∵在 Rt△ABC中,,
∴∠CAB=∠CBA=45°,,
∴BD=AB﹣AD=6﹣2=4.
∵△CAD≌△CBE(SAS),
∴BE=AD=2,∠CBE=∠CAD=45°,
∴∠ABE=∠ABC+∠CBE=90°.
∴,
∴在 Rt△CDE 中,;
(3)解:存在,理由:
由(2)可知,AD2+BD2=BE2+BD2=DE2=2CD2,
∴当CD最小时,有 AD2+BD2 的值最小,此时 CD⊥AB.
∵△ABC 为等腰直角三角形,
∴,
∴AD2+BD2=2CD2≥2×32=18.
即 AD2+BD2 的最小值为18.
14.【解答】(1)解:∵四边形ABCD是正方形,
∴∠ADN=∠ADC=∠B=90°,AD=AB,
∵BM=DN,
∴△ADN≌△ABM(SAS),
∴BM=CN,∠DAN=∠BAM,
∴∠DAN+∠DAM=∠BAM+∠DAM=∠BAD=90°,
∴∠MAN=90°,
∴AM⊥AN,
故答案为:垂直且相等;
(2)解:∵∠H=∠H,∠HEG=∠MAH,
∴△HEF∽△HAM,
∴,
∵线段EH绕点E逆时针旋转得到线段EG,
∴EH=EG=EF+FG=9,
∴AM=HE=9,
∴,
∴AH;
(3)证明:如图,
延长MB至X,使BX=BM,作∠AMR=∠H,交AX于R,
∴XM=2BM,
∵AB⊥XM,
∴AX=AM,
∴∠XAB=∠BAM,∠X=∠AMB,
设∠XAB=∠BAM=α,
∴∠MAH=∠XAM=∠HEF=2α,∠X=∠AMB=90°﹣α,
∴∠AMR=∠H=90°﹣∠BAH=90°﹣3α,
∴∠MRX=∠XAM+∠AMR=2α+(90°﹣3α)=90°﹣α,
∴∠X=∠MRX,
∴RM=XM,
∵∠XAM=∠HEF=2α,∠AMR=∠H,EH=AM,
∴△HEF≌△MAR(ASA),
∴FH=RM=XM=2BM.
15.【解答】(1)解:∵线段AB绕点A逆时针旋转α至AD,α=20°,
∴∠BAD=20°,AB=AD,
∴∠ADB=∠ABD(180°﹣20°)=80°,
又∵∠BAC=90°,
∴∠DAC=70°,
∵AE平分∠DAC,
∴∠DAE∠DAC=35°,
∴∠AEB=∠ADB﹣∠DAE=80°﹣35°=45°,
故答案为:45°;
(2)证明:延长DB到F,使BF=CE,连接AF,
∵AB=AC,AD=AB,
∴AD=AC,
∵AE平分∠DAC,
∴∠DAE=∠CAE,
又∵AE=AE,
∴△ADE≌△ACE(SAS),
∴∠DEA=∠CEA,∠ADE=∠ACE,DE=CE,
∵AB=AD,
∴∠ABD=∠ADB,
∵∠ADE+∠ADB=180°,
∴∠ACE+∠ABD=180°,
∵∠BAC=90°,
∴∠BEC=360°﹣(∠ACE+∠ABD)﹣∠BAC=360°﹣180°﹣90°=90°,
∵∠DEA=∠CEA,
∴∠DEA=∠CEA90°=45°,
∵∠ABF+∠ABD=180°,∠ACE+∠ABD=180°,
∴∠ABF=∠ACE,
∵AB=AC,BF=CE,
∴△ABF≌△ACE(SAS),
∴AF=AE,∠AFB=∠AEC=45°,
∴∠FAE=180°﹣45°﹣45°=90°,
在Rt△AFE中,∠FAE=90°,
∵cos∠AEF,
∴EF,
∵EF=BF+BD+DE=CE+BD+CE=BD+2CE,
∴BD+2CEAE;
(3)解:如图3,当0°<α<90°时,
由(2)可知BD+2CEAE,CE=DE,
∵AE=2CE,
∴BD+2DE=2DE,
∴2;
如图4,当90°<α<180°时,
在BD上截取BF=DE,连接AF,方法同(2)可证△ADE≌△ACE(SAS),
∴DE=CE,
∵AB=AC=AD,
∴∠ABF=∠ADE,
∴△ABF≌△ADE(SAS),
∴AF=AE,∠BAF=∠DAE,
又∵∠DAE=∠CAE,
∴∠BAF=∠CAE,
∴∠EAF=∠FAC+∠CAE=∠FAC+∠BAF=∠BAC=90°,
∴△AEF是等腰直角三角形,
∴EFAE,
∴BD=BF+DE+EF=2DEAE,
∵AE=2CE=2DE,
∴BD=2DE+2DE,
∴2.
综上所述,的值为22或22.
16.【解答】(1)证明:如图1,
作AH⊥BC于H,
∵AB=AC,
∴∠BAH=∠CAH60°,BC=2BH,
∴sin60°,
∴BH,
∴BC=2BH;
(2)解:∵AB=AC,
∴∠ABC=∠ACB30°,
由(1)得,
,
同理可得,
∠DBE=30°,,
∴∠ABC=∠DBE,,
∴∠ABC﹣∠DBC=∠DBE﹣∠DBC,
∴∠ABD=∠CBE,
∴△ABD∽△CBE,
∴;
(3)解:如图2,
当点D在线段AC上时,
作BF⊥AC,交CA的延长线于F,作AG⊥BD于G,
设AB=AC=3a,则AD=2a,
由(1)得,CE,
在Rt△ABF中,∠BAF=180°﹣∠BAC=60°,AB=3a,
∴AF=3a cos60°,BF=3a.sin60°,
在Rt△BDF中,DF=AD+AF=2aa,
BDa,
∵∠AGD=∠F=90°,∠ADG=∠BDF,
∴△DAG∽△DBF,
∴,
∴,
∴AG,
∵AN∥DE,
∴∠AND=∠BDE=120°,
∴∠ANG=60°,
∴ANaa,
∴,
如图3,
当点D在AC的延长线上时,
设AB=AC=2a,则AD=4a,
由(1)得,
CE4,
作BR⊥CA,交CA的延长线于R,作AQ⊥BD于Q,
同理可得,
AR=a,BR,
∴BD2a,
∴,
∴AQ,
∴ANa,
∴,
综上所述:或.
17.【解答】解:(1)证明:∵PB'⊥AC,∠CAB=90°,
∴PB'∥AB.
∴∠B'PA=∠BAP,
又由折叠可知∠BAP=∠B'AP,
∴∠B'PA=∠B'AP.
故PB′=AB′.
(2)设AB=AC=a,AC、PB'交于点D,如答图1所示,
则△ABC为等腰直角三角形,
∴BC,PC,PB,
由折叠可知,∠PB'A=∠B=45°,
又∠ACB=45°,
∴∠PB'A=∠ACB,
又∠CDP=∠B'DA,
∴△CDP∽△B'DA.
∴.①
设B'D=b,则CDb.
∴AD=AC﹣CD=ab,
PD=PB'﹣B'D=PB﹣B'Db,
由①得:.
解得:b.
过点D作DE⊥AB'于点E,则△B'DE为等腰直角三角形.
∴B'E=sin45°×B'D,
∴AE=AB'﹣B'E=AB﹣B'E=a.
又AD=AC﹣CD=ab=a.
∴cos∠B'AC=cos∠EAD.
(3)存在点P,使得CB'=AB=m.理由如下:
∵∠ACB=30°,∠CAB=90°.
∴BC=2m.
①如答图2所示,
由题意可知,点B'的运动轨迹为以A为圆心、AB为半径的半圆A.
当P为BC中点时,PC=BP=AP=AB'=m,
又∠B=60°,
∴△PAB为等边三角形.
又由折叠可得四边形ABPB'为菱形.
∴PB'∥AB,
∴PB'⊥AC.
又∵AP=AB',
则易知AC为PB'的垂直平分线.
故CB'=PC=AB=m,满足题意.
此时,.
②当点B'落在BC上时,如答图3所示,
此时CB'=AB=m,
则PB',
∴PC=CB'+PB'=m,
∴.
综上所述,的值为或.
21世纪教育网(www.21cnjy.com)
同课章节目录
