2025年九年级数学中考三轮冲刺训练胡不归问题专题训练(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练胡不归问题专题训练(含答案) | 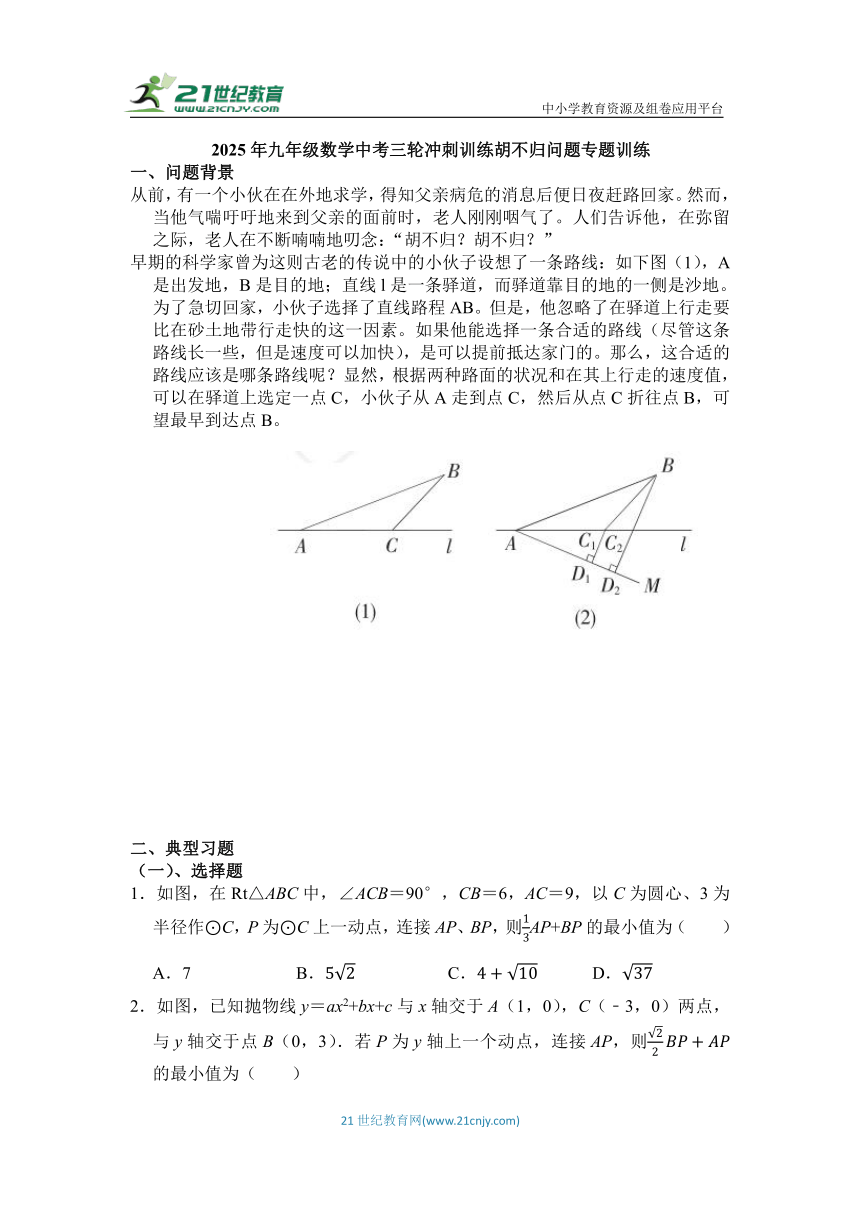 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 19:29:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练胡不归问题专题训练
一、问题背景
从前,有一个小伙在在外地求学,得知父亲病危的消息后便日夜赶路回家。然而,当他气喘吁吁地来到父亲的面前时,老人刚刚咽气了。人们告诉他,在弥留之际,老人在不断喃喃地叨念:“胡不归?胡不归?”
早期的科学家曾为这则古老的传说中的小伙子设想了一条路线:如下图(1),A是出发地,B是目的地;直线l是一条驿道,而驿道靠目的地的一侧是沙地。为了急切回家,小伙子选择了直线路程AB。但是,他忽略了在驿道上行走要比在砂土地带行走快的这一因素。如果他能选择一条合适的路线(尽管这条路线长一些,但是速度可以加快),是可以提前抵达家门的。那么,这合适的路线应该是哪条路线呢?显然,根据两种路面的状况和在其上行走的速度值,可以在驿道上选定一点C,小伙子从A走到点C,然后从点C折往点B,可望最早到达点B。
二、典型习题
(一)、选择题
1.如图,在Rt△ABC中,∠ACB=90°,CB=6,AC=9,以C为圆心、3为半径作⊙C,P为⊙C上一动点,连接AP、BP,则AP+BP的最小值为( )
A.7 B. C. D.
2.如图,已知抛物线y=ax2+bx+c与x轴交于A(1,0),C(﹣3,0)两点,与y轴交于点B(0,3).若P为y轴上一个动点,连接AP,则的最小值为( )
A. B.2 C. D.4
3.如图,在△ACB中,∠A=15°,AB=2,P为AC边上的一个动点(不与A、C重合),连接BP,则AP+PB的最小值是( )
A. B.3 C.1 D.
(二)、填空题
4.如图,在△ABC中,AB=5,tan∠C=2,则ACBC的最大值为 .
5.如图,在△ABC中,AB=5,AC=4,sinA,BD⊥AC交AC于点D.点P为线段BD上的动点,则PCPB的最小值为 .
6.如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .
(三)、解答题
7.如图,在菱形ABCD中,∠ABC=60°,AB=2,E是BC边上一个动点,连接AE,AE的垂直平分线MN交AE于点M,交BD于点N,连接EN、CN.
(1)求证:EN=CN;
(2)求2EN+BN的最小值.
8.如图,已知Rt△ABC中,∠BAC=30°延长BC至D使CD=BC,连接AD.
(1)求证:△ABD是等边三角形;
(2)若E为线段CD的中点,且AD=8,点P为线段AC上一动点,连接EP,BP.求的最小值.
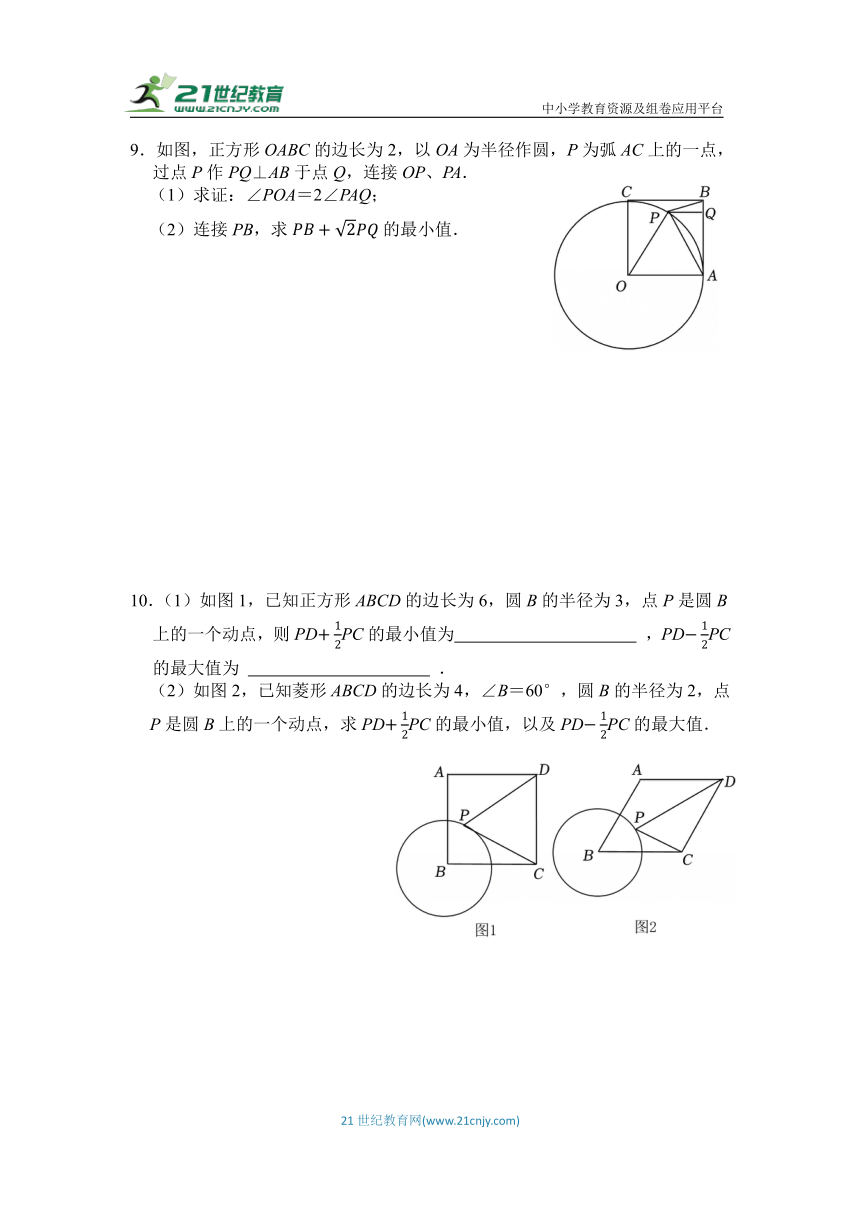
9.如图,正方形OABC的边长为2,以OA为半径作圆,P为弧AC上的一点,过点P作PQ⊥AB于点Q,连接OP、PA.
(1)求证:∠POA=2∠PAQ;
(2)连接PB,求的最小值.
10.(1)如图1,已知正方形ABCD的边长为6,圆B的半径为3,点P是圆B上的一个动点,则PDPC的最小值为 ,PDPC的最大值为 .
(2)如图2,已知菱形ABCD的边长为4,∠B=60°,圆B的半径为2,点P是圆B上的一个动点,求PDPC的最小值,以及PDPC的最大值.
11.如图,已知抛物线y(x﹣2)(x+4)(k为常数,且k大于0)与x轴从左至右依次交于A,B两点,与y轴交于点C,点D在抛物线第一象限的图象上,且∠BAD=30°.
(1)若点D的横坐标为5,求抛物线的函数表达式;
(2)在(1)的条件下,设F是线段AD上一点(不含端点),连接BF,一动点M从点B出发,沿线段BF以每秒1个单位的速度运动到点F,再沿线段FD以每秒2个单位的速度运动到点D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少,最少用时是多少?
12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点C为顶点的正方形CDEF(C,D,E,F四个顶点按逆时针方向排列)可以绕点C自由转动,且 CD,连结AF,BD.
(1)求证:△BDC≌△AFC;
(2)在正方形CDEF旋转过程中,求 BDAD的最小值.
13.抛物线y=x2﹣4x+3与x轴分别交于A、B,与y轴交于点C,点B关于y轴的对称点为点P,在y轴上找一点Q,使PQCQ的值最小,求出最小值,以及此时Q点的坐标.
14.如图,在Rt△AOB中,∠AOB=90°,OB=4,OA=6,⊙O的半径为2,点P是⊙O上一动点,连接AP,BP,求APBP的最小值.
15.如图,四边形ABCD是菱形,AB=4,且∠ABC=60°,M为对角线BD(不含B点)上任意一点.
(1)求AM+BM+CM的最小值;
(2)求AMBM的最小值.
参考答案
一、选择题
题号 1 2 3
答案 D C A
1.【解答】解:在CA上截取CM,使得CM=1,连接PM,PC,BM.
∵PC=3,CM=1,CA=9,
∴PC2=CM CA,
∴,
∵∠PCM=∠ACP,
∴△PCM﹣△ACP,
∴,
∴,
∴,
∵PM+PB≥BM,
在Rt△BCM中,
∵∠BCM=90°,CM=1,BC=6,
∴BM.
∴AP+BP.
则AP+BP的最小值为.
故选:D.
2.【解答】解:连接BC,AP,过点P作PG⊥BC于点G,连接AG,过点A作AH⊥BC于点H,如图,
∵C(﹣3,0),B(0,3),
∴OC=OB,
∴∠OBC=45°,
∴PGBP,
∴PG+AP≥AG≥AH,
∴的最小值为AH的长,
∵A(1,0),C(﹣3,0)
∴AC=1﹣(﹣3)=4,
在Rt△ACH中,
∵∠ACH=45°,AC=4,
∴AHAC,
∴的最小值为.
故选:C.
3.【解答】解:以AP为斜边在AP的下方作等腰直角三角形ADP,则AD=DPAP,
∴AP+PB=DP+PB,
∴当D,P,B在一条直线上时,AP+PB取得最小值.
∵△ADP是等腰直角三角形,
∴∠DAP=45°.
∵∠BAC=15°,
∴∠DAP=60°.
在Rt△ABD中,
∵sin∠BAD,
∴BD=AB sin60°=2.
∴AP+PB的最小值为.
故选:A.
二、填空题、
4.【解答】解:过点B作BD⊥AC,垂足为D,如图1所示:
∵tan∠C=2,
在Rt△BCD中,设DC=x,则BD=2x,由勾股定理可得,
∴,即,
∴,
延长DC到E,使 EC=CD=x,连接BE,如图2所示:
∴,
∵BD⊥DE,DE=2x=BD,
∴△BDE是等腰直角三角形,则∠E=45°,
在△ABE 中,AB=5,∠E=45°,
由辅助圆﹣定弦定角模型,作△ABE的外接圆,如图3所示:
由圆周角定理可知,点E在⊙O上运动,AE是⊙O的弦,求 的最大值就是求弦AE的最大值,根据圆的性质可知,当弦AE过圆心O,即AE是直径时,弦最大,如图4所示:
∵AE是⊙O的直径,
∴∠ABE=90°,
∵∠E=45°,
∴△ABE是等腰直角三角形,
∵AB=5,
∴BE=AB=5,则由勾股定理可得,即 的最大值为,
故答案为:.
5.【解答】解:过点P作PE⊥AB于点E,过点C作CH⊥AB于点H,
∵BD⊥AC,
∴∠ADB=90°,
∵sinA,AB=5,
∴BD=4,
由勾股定理得AD,
∴sin∠ABD,
∴EP,
∴PCPB=PC+PE,
即点C、P、E三点共线时,PCPB最小,
∴PCPB的最小值为CH的长,
∵S△ABC,
∴4×4=5×CH,
∴CH.
∴PCPB的最小值为.
故答案为:.
6.【解答】解:如图,
在∠BAC的外部作∠CAE=15°,作BF⊥AE于F,交AD于P,
此时PA+2PB最小,
∴∠AFB=90°
∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD,
∴∠EAD=∠CAE+∠CAD=30°,
∴PF,
∴PA+2PB=2()=2(PF+PB)=2BF,
在Rt△ABF中,AB=4,∠BAF=∠BAC+∠CAE=45°,
∴BF=AB sin45°=42,
∴(PA+2PB)最小=2BF=4,
故答案为:4.
三、解答题
7.【解答】解:(1)连接AN,如图,
∵四边形ABCD是菱形,
∴点A,点C关于直线BD轴对称,
∴AN=CN,
∵AE的垂直平分线MN交AE于点M,交BD于点N,
∴AN=EN,
∴EN=CN;
(2)过点N作NG⊥BC于点G,连接AN,AG,过点A作AH⊥BC于点H,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠DBC=30°,
∴BN=2NG,
∵AE的垂直平分线MN交AE于点M,交BD于点N,
∴EN=AN,
∴2EN+BN=2AN+2NG=2(AN+NG)≥2AG≥2AH,
∴2EN+BN的最小值为2AH,
∵∠ABC=60°,AB=2,
∴AH=AB sin60°,
∴2EN+BN的最小值为2.
8.【解答】(1)证明:∵在Rt△ABC中,∠BAC=30°,
∴AC⊥BD,∠B=60°,
∴AD=AB,
∵∠B=60°,
∴△ABD是等边三角形.
(2)如图,作PF⊥AB于F,EF′⊥AB于F′,交AC于P′,
∵∠PAF=30°,∠PFA=90°,
∴,
∴,
∴当E、P、F共线时,即EF′⊥AB时,PE+PF最短,最小值为线段EF′,
∴,
∵∠B=60°,
∴∠BEF′=30°,
∴
∴,
∴的最小值为.
9.【解答】(1)证明:延长AO,交圆O于点Q,连接PQ,
∵AQ为圆O的直径,
∴∠QPA=90°,即∠QPO+∠OPA=90°,
∵正方形OABC,
∴∠OAB=90°,即∠PAB+∠OAP=90°,
∵OP=OA,
∴∠OPA=∠OAP,
∴∠QPO=∠OAP,
∵OP=OQ,
∴∠QPO=∠PQO,
∵∠POA为△OPQ的外角,
∴∠POA=2∠QPO,
则∠POA=2∠PAQ;
(2)解:延长QP到F,使PF=PQ,在PF下方作正方形PFGN,连接PG,此时PGPFPQ,
要使PBPQ最小,即为BP+PG最小,如图所示,当B、P、Q三点共线,且在OB上时最小值为BG,
∵正方形OABC的边长为2,
∴OBOA=2,
∵OP=OA=2,
∴PB=OB﹣OP=22,PQ=PFPB=2,
∴PQPF=22,即BG=44,
则PBPQ的最小值为44.
10.【解答】解:(1)如图1,
在BC上截取BE,
∴,
∵∠PBE=∠PBC,
∴△PBE∽△CBP,
∴,
∴PEPC,
∴PDPC=PD+PE≥DE,
PDPC=PD﹣PE≤DE,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴DE,
∴PDPC的最小值为:,此时点P在P′处,
PDPC的最大值为:,此时点P在P″处,
故答案为:,;
(2)如图2,
在BC上截取BE=1,作DF⊥BC交BC的延长线于F,
∴,
∵∠PBE=∠PBC,
∴△PBE∽△CBP,
∴,
∴PEPC,
∴PDPC=PD+PE≥DE,
PDPC=PD﹣PE≤DE,
在Rt△DCF中,∠DCF=∠ABC=60°,CD=4,
∴CF=4 cos60°=2,DF=4 sin60°=2,
在Rt△DEF中,DF=2,EF=CE+CF=3+2=5,
∴DE,
∴PDPC的最小值为:,此时点P在P′处,
PDPC的最大值为:,此时点P在P″处,
11.【解答】解:(1)抛物线y(x﹣2)(x+4),
令y=0得,(x﹣2)(x+4)=0,
解得x=2或x=﹣4,
∴A(﹣4,0),B(2,0),
∴OA=4,
过点D作DE⊥x轴于E,
∴OE=5,AE=9,
∵∠BAD=30°,
∴DE=tan30°×AE=93,
∴D(5,3),
∵点D在抛物线y(x﹣2)(x+4)的图象上,
∴(x﹣2)(x+4)=3,
∴k,
∴抛物线的函数解析式为:y(x﹣2)(x+4),
即y;
(2)过点D作x轴的平行线,过点B作BH∥y轴交平行线于H,交AD于F,
∴∠HDF=∠DAB=30°,
∴HFDF,
由题意知:动点M的运动路径为BF+DF,
∴点M的运动时间t=BFDF=BF+HF,
根据垂线段最短得:t的最小值为BH的长,
即t=3秒,
此时F的横坐标为2,
设AD的解析式为:y=kx+b,
将(﹣4,0),(5,3)代入得:
,
解得:,
∴直线AD的解析式为:y,
当x=2时,y=2,
∴F(1,2).
∴当点F的坐标为(2,2)时,点M在整个运动过程中用时最少,为3秒.
12.【解答】(1)证明:∵四边形CDEF是正方形,
∴CF=CD,∠FCD=∠ACB=90°,
∴∠ACF=∠BCD,
∵AC=CB,
∴△FCA≌△DCB(SAS).
(2)解:如图.取AC的中点M.连接DM,BM.
∵CD,CA=2,CM=1,
∴CD2=CM CA,
∴,
∵∠DCM=∠ACD,
∴△DCM∽△ACD,
∴,
∴DMAD,
∴BDAD=BD+DM≥BM,
∴BDAD的最小值为BM的长,
∵BM,
∴BDAD的最小值为.
13.【解答】解:如图,
连接AC,过点Q作QD⊥AC于D,
由x2﹣4x+3=0得,
x1=1,x2=3,
∴A (1,0),B(3,0),P(﹣3,0),
当x=0时,y=3,
∴C(0,3),
∴AC,
∴sin∠ACO,cos∠ACO,
∴DQCQ,
∴PQCQ=PQ+DQ,
∴当点P、Q、D共线时,PQCQ最小,
∵∠PDA=∠AOC=90°,
∴∠ACO+∠CAO=90°,∠APD+∠CAO=90°,
∴∠APD=∠ACO,
∴PD=PA cos∠APD=4 cos∠ACO=4,
∴PQCQ的最小值为:,
∵OP=OC,
∴△POQ≌△COA(ASA),
∴OQ=OA=1,
∴Q(0,1).
14.【解答】解:在OB上取点Q,使OQ=1,连接PO,PQ,AQ,
∵,,
∴,
∵∠POQ=∠POB,
∴△POQ∽△BOP,
∴,
∴PQPB,
∴APPB=AP+PQ,
当APBP的值最小,只需AP+PQ最小,
∴当A,P,Q三点共线时,AP+PQ最小,最小值是AQ的长,
此时:AQ.
∴APPB的最小值是.
15.【解答】解:(1)连接AC,MC,将△BCM绕点B逆时针旋转60°得△BAM′,再将△BAM绕点B逆时针旋转60°得△BA′M′,连接CA′,与AB交于点E,如图,则A′M′=AM,BM′=BM,A′B=AB=BC=4,∠ABA′=∠ABC=60°,∠ABM′=∠CBM=∠ABM=30°,
∴△BMM′是等边三角形,BE⊥A′C,
∴BM=MM′,
∴AM+BM+CM=A′M+MM′+CM≥A′C,
当A′、M′、M、C四点共线时,AM+BM+CM=A′M+MM′+CM=A′C的值最小,
此时A′C=2CE=2.
故AM+BM+CM的最小值为4;
(2)如图,过点A作AT⊥BC于T,过点M作MH⊥BC于H.
∵四边形ABCD是菱形,∠ABC=60°,
∴∠DBC∠ABC=30°,
∵MH⊥BC,
∴∠BHM=90°,
∴MHBM,
∴AMBM=AM+MH,
∵AT⊥BC,
∴∠ATB=90°,
∴AT=AB sin60°=2,
∵AM+MH≥AT,
∴AM+MH≥2,
∴AMBM≥2,
∴AMBM的最小值为2,
故答案为:2.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练胡不归问题专题训练
一、问题背景
从前,有一个小伙在在外地求学,得知父亲病危的消息后便日夜赶路回家。然而,当他气喘吁吁地来到父亲的面前时,老人刚刚咽气了。人们告诉他,在弥留之际,老人在不断喃喃地叨念:“胡不归?胡不归?”
早期的科学家曾为这则古老的传说中的小伙子设想了一条路线:如下图(1),A是出发地,B是目的地;直线l是一条驿道,而驿道靠目的地的一侧是沙地。为了急切回家,小伙子选择了直线路程AB。但是,他忽略了在驿道上行走要比在砂土地带行走快的这一因素。如果他能选择一条合适的路线(尽管这条路线长一些,但是速度可以加快),是可以提前抵达家门的。那么,这合适的路线应该是哪条路线呢?显然,根据两种路面的状况和在其上行走的速度值,可以在驿道上选定一点C,小伙子从A走到点C,然后从点C折往点B,可望最早到达点B。
二、典型习题
(一)、选择题
1.如图,在Rt△ABC中,∠ACB=90°,CB=6,AC=9,以C为圆心、3为半径作⊙C,P为⊙C上一动点,连接AP、BP,则AP+BP的最小值为( )
A.7 B. C. D.
2.如图,已知抛物线y=ax2+bx+c与x轴交于A(1,0),C(﹣3,0)两点,与y轴交于点B(0,3).若P为y轴上一个动点,连接AP,则的最小值为( )
A. B.2 C. D.4
3.如图,在△ACB中,∠A=15°,AB=2,P为AC边上的一个动点(不与A、C重合),连接BP,则AP+PB的最小值是( )
A. B.3 C.1 D.
(二)、填空题
4.如图,在△ABC中,AB=5,tan∠C=2,则ACBC的最大值为 .
5.如图,在△ABC中,AB=5,AC=4,sinA,BD⊥AC交AC于点D.点P为线段BD上的动点,则PCPB的最小值为 .
6.如图,在△ABC中,AB=AC=4,∠CAB=30°,AD⊥BC,垂足为D,P为线段AD上的一动点,连接PB、PC.则PA+2PB的最小值为 .
(三)、解答题
7.如图,在菱形ABCD中,∠ABC=60°,AB=2,E是BC边上一个动点,连接AE,AE的垂直平分线MN交AE于点M,交BD于点N,连接EN、CN.
(1)求证:EN=CN;
(2)求2EN+BN的最小值.
8.如图,已知Rt△ABC中,∠BAC=30°延长BC至D使CD=BC,连接AD.
(1)求证:△ABD是等边三角形;
(2)若E为线段CD的中点,且AD=8,点P为线段AC上一动点,连接EP,BP.求的最小值.
9.如图,正方形OABC的边长为2,以OA为半径作圆,P为弧AC上的一点,过点P作PQ⊥AB于点Q,连接OP、PA.
(1)求证:∠POA=2∠PAQ;
(2)连接PB,求的最小值.
10.(1)如图1,已知正方形ABCD的边长为6,圆B的半径为3,点P是圆B上的一个动点,则PDPC的最小值为 ,PDPC的最大值为 .
(2)如图2,已知菱形ABCD的边长为4,∠B=60°,圆B的半径为2,点P是圆B上的一个动点,求PDPC的最小值,以及PDPC的最大值.
11.如图,已知抛物线y(x﹣2)(x+4)(k为常数,且k大于0)与x轴从左至右依次交于A,B两点,与y轴交于点C,点D在抛物线第一象限的图象上,且∠BAD=30°.
(1)若点D的横坐标为5,求抛物线的函数表达式;
(2)在(1)的条件下,设F是线段AD上一点(不含端点),连接BF,一动点M从点B出发,沿线段BF以每秒1个单位的速度运动到点F,再沿线段FD以每秒2个单位的速度运动到点D后停止,当点F的坐标是多少时,点M在整个运动过程中用时最少,最少用时是多少?
12.如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点C为顶点的正方形CDEF(C,D,E,F四个顶点按逆时针方向排列)可以绕点C自由转动,且 CD,连结AF,BD.
(1)求证:△BDC≌△AFC;
(2)在正方形CDEF旋转过程中,求 BDAD的最小值.
13.抛物线y=x2﹣4x+3与x轴分别交于A、B,与y轴交于点C,点B关于y轴的对称点为点P,在y轴上找一点Q,使PQCQ的值最小,求出最小值,以及此时Q点的坐标.
14.如图,在Rt△AOB中,∠AOB=90°,OB=4,OA=6,⊙O的半径为2,点P是⊙O上一动点,连接AP,BP,求APBP的最小值.
15.如图,四边形ABCD是菱形,AB=4,且∠ABC=60°,M为对角线BD(不含B点)上任意一点.
(1)求AM+BM+CM的最小值;
(2)求AMBM的最小值.
参考答案
一、选择题
题号 1 2 3
答案 D C A
1.【解答】解:在CA上截取CM,使得CM=1,连接PM,PC,BM.
∵PC=3,CM=1,CA=9,
∴PC2=CM CA,
∴,
∵∠PCM=∠ACP,
∴△PCM﹣△ACP,
∴,
∴,
∴,
∵PM+PB≥BM,
在Rt△BCM中,
∵∠BCM=90°,CM=1,BC=6,
∴BM.
∴AP+BP.
则AP+BP的最小值为.
故选:D.
2.【解答】解:连接BC,AP,过点P作PG⊥BC于点G,连接AG,过点A作AH⊥BC于点H,如图,
∵C(﹣3,0),B(0,3),
∴OC=OB,
∴∠OBC=45°,
∴PGBP,
∴PG+AP≥AG≥AH,
∴的最小值为AH的长,
∵A(1,0),C(﹣3,0)
∴AC=1﹣(﹣3)=4,
在Rt△ACH中,
∵∠ACH=45°,AC=4,
∴AHAC,
∴的最小值为.
故选:C.
3.【解答】解:以AP为斜边在AP的下方作等腰直角三角形ADP,则AD=DPAP,
∴AP+PB=DP+PB,
∴当D,P,B在一条直线上时,AP+PB取得最小值.
∵△ADP是等腰直角三角形,
∴∠DAP=45°.
∵∠BAC=15°,
∴∠DAP=60°.
在Rt△ABD中,
∵sin∠BAD,
∴BD=AB sin60°=2.
∴AP+PB的最小值为.
故选:A.
二、填空题、
4.【解答】解:过点B作BD⊥AC,垂足为D,如图1所示:
∵tan∠C=2,
在Rt△BCD中,设DC=x,则BD=2x,由勾股定理可得,
∴,即,
∴,
延长DC到E,使 EC=CD=x,连接BE,如图2所示:
∴,
∵BD⊥DE,DE=2x=BD,
∴△BDE是等腰直角三角形,则∠E=45°,
在△ABE 中,AB=5,∠E=45°,
由辅助圆﹣定弦定角模型,作△ABE的外接圆,如图3所示:
由圆周角定理可知,点E在⊙O上运动,AE是⊙O的弦,求 的最大值就是求弦AE的最大值,根据圆的性质可知,当弦AE过圆心O,即AE是直径时,弦最大,如图4所示:
∵AE是⊙O的直径,
∴∠ABE=90°,
∵∠E=45°,
∴△ABE是等腰直角三角形,
∵AB=5,
∴BE=AB=5,则由勾股定理可得,即 的最大值为,
故答案为:.
5.【解答】解:过点P作PE⊥AB于点E,过点C作CH⊥AB于点H,
∵BD⊥AC,
∴∠ADB=90°,
∵sinA,AB=5,
∴BD=4,
由勾股定理得AD,
∴sin∠ABD,
∴EP,
∴PCPB=PC+PE,
即点C、P、E三点共线时,PCPB最小,
∴PCPB的最小值为CH的长,
∵S△ABC,
∴4×4=5×CH,
∴CH.
∴PCPB的最小值为.
故答案为:.
6.【解答】解:如图,
在∠BAC的外部作∠CAE=15°,作BF⊥AE于F,交AD于P,
此时PA+2PB最小,
∴∠AFB=90°
∵AB=AC,AD⊥BC,
∴∠CAD=∠BAD,
∴∠EAD=∠CAE+∠CAD=30°,
∴PF,
∴PA+2PB=2()=2(PF+PB)=2BF,
在Rt△ABF中,AB=4,∠BAF=∠BAC+∠CAE=45°,
∴BF=AB sin45°=42,
∴(PA+2PB)最小=2BF=4,
故答案为:4.
三、解答题
7.【解答】解:(1)连接AN,如图,
∵四边形ABCD是菱形,
∴点A,点C关于直线BD轴对称,
∴AN=CN,
∵AE的垂直平分线MN交AE于点M,交BD于点N,
∴AN=EN,
∴EN=CN;
(2)过点N作NG⊥BC于点G,连接AN,AG,过点A作AH⊥BC于点H,
∵四边形ABCD是菱形,∠ABC=60°,
∴∠DBC=30°,
∴BN=2NG,
∵AE的垂直平分线MN交AE于点M,交BD于点N,
∴EN=AN,
∴2EN+BN=2AN+2NG=2(AN+NG)≥2AG≥2AH,
∴2EN+BN的最小值为2AH,
∵∠ABC=60°,AB=2,
∴AH=AB sin60°,
∴2EN+BN的最小值为2.
8.【解答】(1)证明:∵在Rt△ABC中,∠BAC=30°,
∴AC⊥BD,∠B=60°,
∴AD=AB,
∵∠B=60°,
∴△ABD是等边三角形.
(2)如图,作PF⊥AB于F,EF′⊥AB于F′,交AC于P′,
∵∠PAF=30°,∠PFA=90°,
∴,
∴,
∴当E、P、F共线时,即EF′⊥AB时,PE+PF最短,最小值为线段EF′,
∴,
∵∠B=60°,
∴∠BEF′=30°,
∴
∴,
∴的最小值为.
9.【解答】(1)证明:延长AO,交圆O于点Q,连接PQ,
∵AQ为圆O的直径,
∴∠QPA=90°,即∠QPO+∠OPA=90°,
∵正方形OABC,
∴∠OAB=90°,即∠PAB+∠OAP=90°,
∵OP=OA,
∴∠OPA=∠OAP,
∴∠QPO=∠OAP,
∵OP=OQ,
∴∠QPO=∠PQO,
∵∠POA为△OPQ的外角,
∴∠POA=2∠QPO,
则∠POA=2∠PAQ;
(2)解:延长QP到F,使PF=PQ,在PF下方作正方形PFGN,连接PG,此时PGPFPQ,
要使PBPQ最小,即为BP+PG最小,如图所示,当B、P、Q三点共线,且在OB上时最小值为BG,
∵正方形OABC的边长为2,
∴OBOA=2,
∵OP=OA=2,
∴PB=OB﹣OP=22,PQ=PFPB=2,
∴PQPF=22,即BG=44,
则PBPQ的最小值为44.
10.【解答】解:(1)如图1,
在BC上截取BE,
∴,
∵∠PBE=∠PBC,
∴△PBE∽△CBP,
∴,
∴PEPC,
∴PDPC=PD+PE≥DE,
PDPC=PD﹣PE≤DE,
∵四边形ABCD是正方形,
∴∠BCD=90°,
∴DE,
∴PDPC的最小值为:,此时点P在P′处,
PDPC的最大值为:,此时点P在P″处,
故答案为:,;
(2)如图2,
在BC上截取BE=1,作DF⊥BC交BC的延长线于F,
∴,
∵∠PBE=∠PBC,
∴△PBE∽△CBP,
∴,
∴PEPC,
∴PDPC=PD+PE≥DE,
PDPC=PD﹣PE≤DE,
在Rt△DCF中,∠DCF=∠ABC=60°,CD=4,
∴CF=4 cos60°=2,DF=4 sin60°=2,
在Rt△DEF中,DF=2,EF=CE+CF=3+2=5,
∴DE,
∴PDPC的最小值为:,此时点P在P′处,
PDPC的最大值为:,此时点P在P″处,
11.【解答】解:(1)抛物线y(x﹣2)(x+4),
令y=0得,(x﹣2)(x+4)=0,
解得x=2或x=﹣4,
∴A(﹣4,0),B(2,0),
∴OA=4,
过点D作DE⊥x轴于E,
∴OE=5,AE=9,
∵∠BAD=30°,
∴DE=tan30°×AE=93,
∴D(5,3),
∵点D在抛物线y(x﹣2)(x+4)的图象上,
∴(x﹣2)(x+4)=3,
∴k,
∴抛物线的函数解析式为:y(x﹣2)(x+4),
即y;
(2)过点D作x轴的平行线,过点B作BH∥y轴交平行线于H,交AD于F,
∴∠HDF=∠DAB=30°,
∴HFDF,
由题意知:动点M的运动路径为BF+DF,
∴点M的运动时间t=BFDF=BF+HF,
根据垂线段最短得:t的最小值为BH的长,
即t=3秒,
此时F的横坐标为2,
设AD的解析式为:y=kx+b,
将(﹣4,0),(5,3)代入得:
,
解得:,
∴直线AD的解析式为:y,
当x=2时,y=2,
∴F(1,2).
∴当点F的坐标为(2,2)时,点M在整个运动过程中用时最少,为3秒.
12.【解答】(1)证明:∵四边形CDEF是正方形,
∴CF=CD,∠FCD=∠ACB=90°,
∴∠ACF=∠BCD,
∵AC=CB,
∴△FCA≌△DCB(SAS).
(2)解:如图.取AC的中点M.连接DM,BM.
∵CD,CA=2,CM=1,
∴CD2=CM CA,
∴,
∵∠DCM=∠ACD,
∴△DCM∽△ACD,
∴,
∴DMAD,
∴BDAD=BD+DM≥BM,
∴BDAD的最小值为BM的长,
∵BM,
∴BDAD的最小值为.
13.【解答】解:如图,
连接AC,过点Q作QD⊥AC于D,
由x2﹣4x+3=0得,
x1=1,x2=3,
∴A (1,0),B(3,0),P(﹣3,0),
当x=0时,y=3,
∴C(0,3),
∴AC,
∴sin∠ACO,cos∠ACO,
∴DQCQ,
∴PQCQ=PQ+DQ,
∴当点P、Q、D共线时,PQCQ最小,
∵∠PDA=∠AOC=90°,
∴∠ACO+∠CAO=90°,∠APD+∠CAO=90°,
∴∠APD=∠ACO,
∴PD=PA cos∠APD=4 cos∠ACO=4,
∴PQCQ的最小值为:,
∵OP=OC,
∴△POQ≌△COA(ASA),
∴OQ=OA=1,
∴Q(0,1).
14.【解答】解:在OB上取点Q,使OQ=1,连接PO,PQ,AQ,
∵,,
∴,
∵∠POQ=∠POB,
∴△POQ∽△BOP,
∴,
∴PQPB,
∴APPB=AP+PQ,
当APBP的值最小,只需AP+PQ最小,
∴当A,P,Q三点共线时,AP+PQ最小,最小值是AQ的长,
此时:AQ.
∴APPB的最小值是.
15.【解答】解:(1)连接AC,MC,将△BCM绕点B逆时针旋转60°得△BAM′,再将△BAM绕点B逆时针旋转60°得△BA′M′,连接CA′,与AB交于点E,如图,则A′M′=AM,BM′=BM,A′B=AB=BC=4,∠ABA′=∠ABC=60°,∠ABM′=∠CBM=∠ABM=30°,
∴△BMM′是等边三角形,BE⊥A′C,
∴BM=MM′,
∴AM+BM+CM=A′M+MM′+CM≥A′C,
当A′、M′、M、C四点共线时,AM+BM+CM=A′M+MM′+CM=A′C的值最小,
此时A′C=2CE=2.
故AM+BM+CM的最小值为4;
(2)如图,过点A作AT⊥BC于T,过点M作MH⊥BC于H.
∵四边形ABCD是菱形,∠ABC=60°,
∴∠DBC∠ABC=30°,
∵MH⊥BC,
∴∠BHM=90°,
∴MHBM,
∴AMBM=AM+MH,
∵AT⊥BC,
∴∠ATB=90°,
∴AT=AB sin60°=2,
∵AM+MH≥AT,
∴AM+MH≥2,
∴AMBM≥2,
∴AMBM的最小值为2,
故答案为:2.
21世纪教育网(www.21cnjy.com)
同课章节目录
