2025年九年级数学中考三轮冲刺训练相似形综合压轴题训练(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练相似形综合压轴题训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 19:29:28 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练相似形综合压轴题训练
1.在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
2.如图1,在矩形ABCD中,点E为AD边上不与端点重合的一动点,点F是对角线BD上一点,连接BE,AF交于点O,且∠ABE=∠DAF.
【模型建立】
(1)求证:AF⊥BE;
【模型应用】
(2)若AB=2,AD=3,DFBF,求DE的长;
【模型迁移】
(3)如图2,若矩形ABCD是正方形,DFBF,求的值.
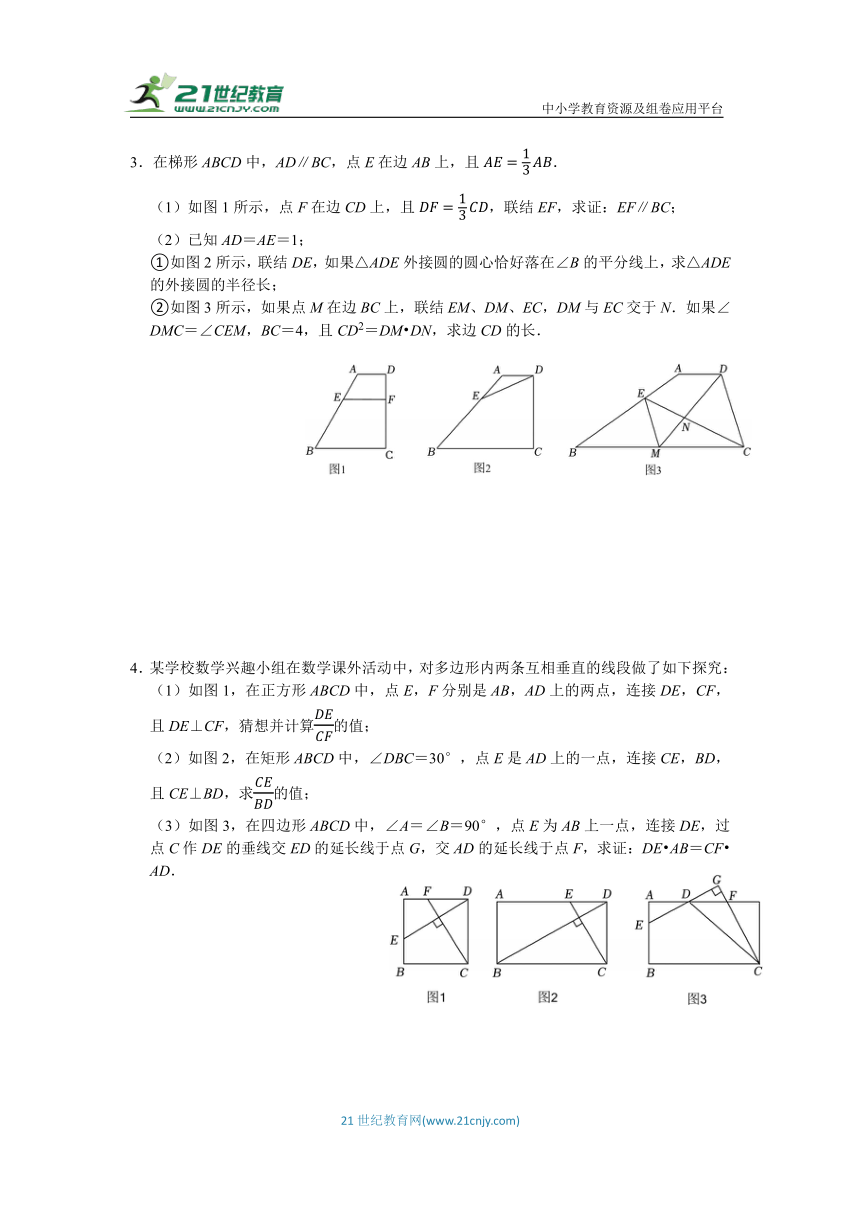
3.在梯形ABCD中,AD∥BC,点E在边AB上,且.
(1)如图1所示,点F在边CD上,且,联结EF,求证:EF∥BC;
(2)已知AD=AE=1;
①如图2所示,联结DE,如果△ADE外接圆的圆心恰好落在∠B的平分线上,求△ADE的外接圆的半径长;
②如图3所示,如果点M在边BC上,联结EM、DM、EC,DM与EC交于N.如果∠DMC=∠CEM,BC=4,且CD2=DM DN,求边CD的长.
4.某学校数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
(1)如图1,在正方形ABCD中,点E,F分别是AB,AD上的两点,连接DE,CF,且DE⊥CF,猜想并计算的值;
(2)如图2,在矩形ABCD中,∠DBC=30°,点E是AD上的一点,连接CE,BD,且CE⊥BD,求的值;
(3)如图3,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE AB=CF AD.
5.如图1, ABCD的对角线AC与BD交于点O,点M,N分别在边AD,BC上,且AM=CN.点E,F分别是BD与AN,CM的交点.
(1)求证:OE=OF;
(2)连接BM交AC于点H,连接HE,HF.
(ⅰ)如图2,若HE∥AB,求证:HF∥AD;
(ⅱ)如图3,若 ABCD为菱形,且MD=2AM,∠EHF=60°,求的值.
6.(1)【观察发现】如图1,在△ABC中,点D在边BC上.若∠BAD=∠C,则AB2=BD BC,请证明;
(2)【灵活运用】如图2,在△ABC中,∠BAC=60°,点D为边BC的中点,CA=CD=2,点E在AB上,连接AD,DE.若∠AED=∠CAD,求BE的长;
(3)【拓展延伸】如图3,在菱形ABCD中,AB=5,点E,F分别在边AD,CD上,∠ABC=2∠EBF,延长AD,BF相交于点G.若BE=4,DG=6,求FG的长.
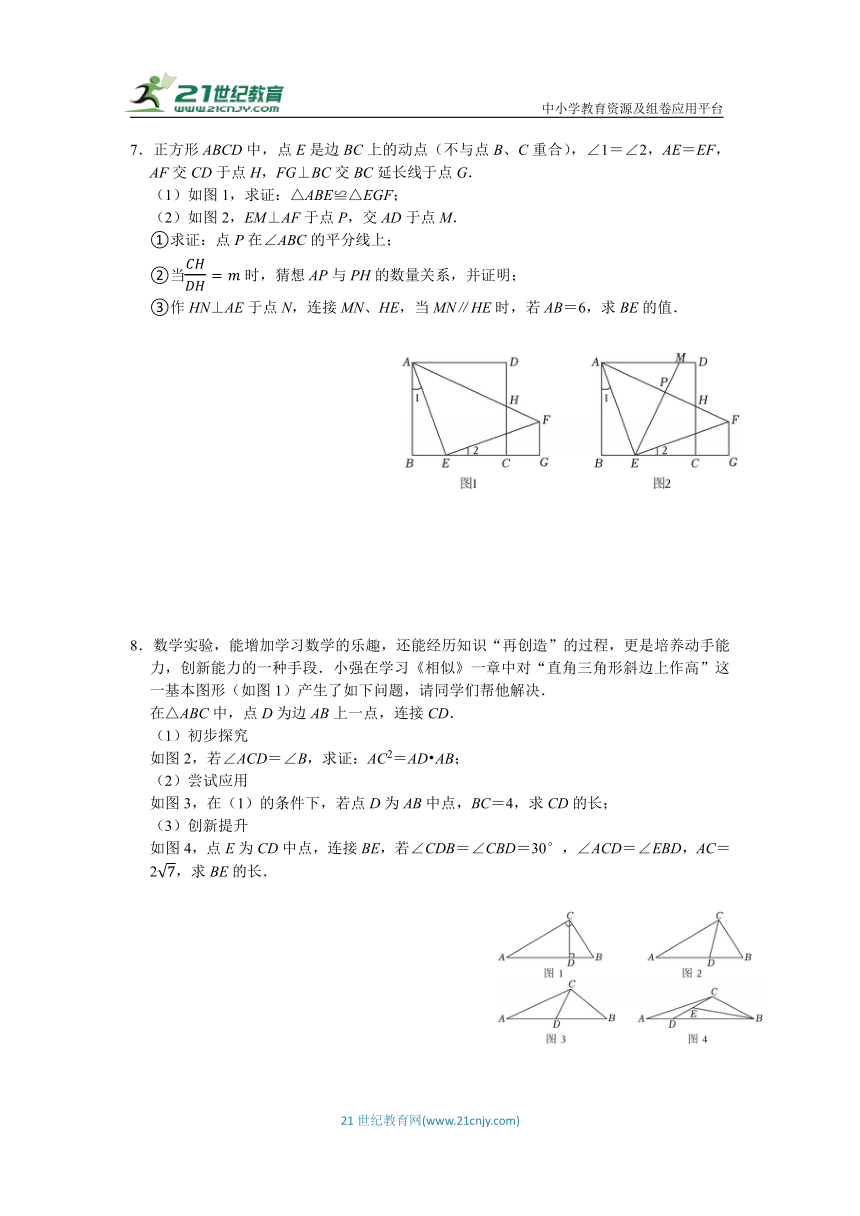
7.正方形ABCD中,点E是边BC上的动点(不与点B、C重合),∠1=∠2,AE=EF,AF交CD于点H,FG⊥BC交BC延长线于点G.
(1)如图1,求证:△ABE≌△EGF;
(2)如图2,EM⊥AF于点P,交AD于点M.
①求证:点P在∠ABC的平分线上;
②当时,猜想AP与PH的数量关系,并证明;
③作HN⊥AE于点N,连接MN、HE,当MN∥HE时,若AB=6,求BE的值.
8.数学实验,能增加学习数学的乐趣,还能经历知识“再创造”的过程,更是培养动手能力,创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题,请同学们帮他解决.
在△ABC中,点D为边AB上一点,连接CD.
(1)初步探究
如图2,若∠ACD=∠B,求证:AC2=AD AB;
(2)尝试应用
如图3,在(1)的条件下,若点D为AB中点,BC=4,求CD的长;
(3)创新提升
如图4,点E为CD中点,连接BE,若∠CDB=∠CBD=30°,∠ACD=∠EBD,AC=2,求BE的长.
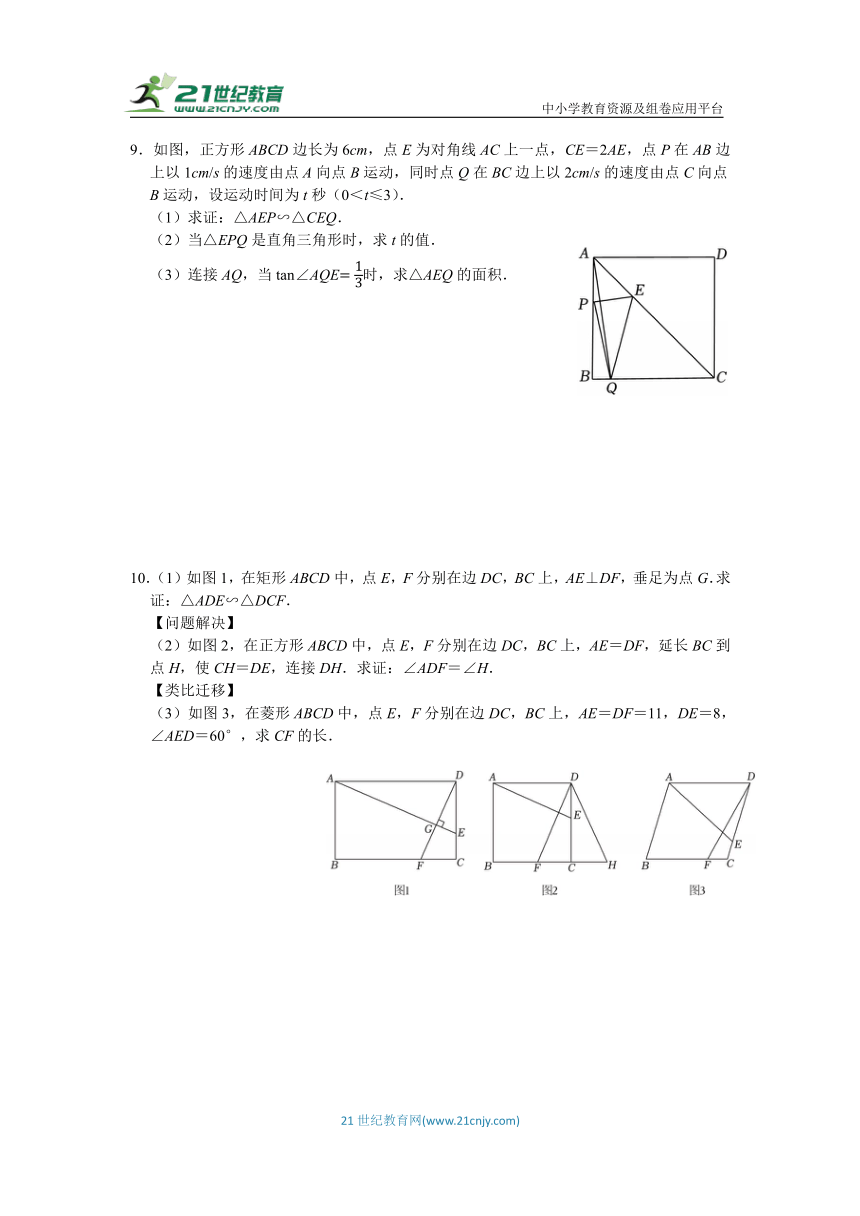
9.如图,正方形ABCD边长为6cm,点E为对角线AC上一点,CE=2AE,点P在AB边上以1cm/s的速度由点A向点B运动,同时点Q在BC边上以2cm/s的速度由点C向点B运动,设运动时间为t秒(0<t≤3).
(1)求证:△AEP∽△CEQ.
(2)当△EPQ是直角三角形时,求t的值.
(3)连接AQ,当tan∠AQE时,求△AEQ的面积.
10.(1)如图1,在矩形ABCD中,点E,F分别在边DC,BC上,AE⊥DF,垂足为点G.求证:△ADE∽△DCF.
【问题解决】
(2)如图2,在正方形ABCD中,点E,F分别在边DC,BC上,AE=DF,延长BC到点H,使CH=DE,连接DH.求证:∠ADF=∠H.
【类比迁移】
(3)如图3,在菱形ABCD中,点E,F分别在边DC,BC上,AE=DF=11,DE=8,∠AED=60°,求CF的长.
11.如图,在正方形ABCD中,E,F分别是边AD,AB上的点,连接CE,EF,CF.
(1)若正方形ABCD的边长为2,E是AD的中点.
①如图1,当∠FEC=90°时,求证:△AEF∽△DCE;
②如图2,当tan∠FCE时,求AF的长;
(2)如图3,延长CF,DA交于点G,当GE=DE,sin∠FCE时,求证:AE=AF.
12.如图,在Rt△ABC中,∠ACB=90°,AC>BC,点D在边AC上,将线段DA绕点D按顺时针方向旋转90°得到DA′,线段DA′交AB于点E,作A′F⊥AB于点F,与线段AC交于点G,连接FC,GB.
(1)求证:△ADE≌△A′DG;
(2)求证:AF GB=AG FC;
(3)若AC=8,tanA,当A′G平分四边形DCBE的面积时,求AD的长.
13.如图1,AB为半圆O的直径,C为BA延长线上一点,CD切半圆于点D,BE⊥CD,交CD延长线于点E,交半圆于点F,已知OA,AC=1.如图2,连结AF,P为线段AF上一点,过点P作BC的平行线分别交CE,BE于点M,N,过点P作PH⊥AB于点H.设PH=x,MN=y.
(1)求CE的长和y关于x的函数表达式;
(2)当PH<PN,且长度分别等于PH,PN,a的三条线段组成的三角形与△BCE相似时,求a的值;
(3)延长PN交半圆O于点Q,当NQx﹣3时,求MN的长.
14.已知正方形ABCD,E是对角线AC上一点.
(1)如图1,连接BE,DE.求证:△ABE≌△ADE;
(2)如图2,F是DE延长线上一点,DF交AB于点G,BF⊥BE.判断△FBG的形状并说明理由;
(3)在第(2)题的条件下,BE=BF=2.求的值.
15.如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,点E为BC边上的动点(不与B、C重合,过点E作直线AB的垂线,垂足为F,连接DE、DF.
(1)求证:△ABM∽△EBF;
(2)当点E为BC的中点时,求DE的长;
(3)设BE=x,△DEF的面积为y,求y与x之间的函数关系式,并求当x为何值时,y有最大值,最大值是多少?
16.如图1,在矩形ABCD中,AB=4,BC=6.点E是线段AD上的动点(点E不与点A,D重合),连接CE,过点E作EF⊥CE,交AB于点F.
(1)求证:△AEF∽△DCE;
(2)如图2,连接CF,过点B作BG⊥CF,垂足为G,连接AG.点M是线段BC的中点,连接GM.
①求AG+GM的最小值;
②当AG+GM取最小值时,求线段DE的长.
17.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=CD,O是对角线AC的中点,联结BO并延长交边CD或边AD于点E.
(1)当点E在CD上,
①求证:△DAC∽△OBC;
②若BE⊥CD,求的值;
(2)若DE=2,OE=3,求CD的长.
参考答案
1.【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴DP=CP1,
设EP=AE=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得x,
∴EP=AP=x,
∴ED=AD﹣AE,
∵△EDP∽△PCH,
∴,即,
∴PH,
∵PG=AB=2,
∴GH=PG﹣PH.
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴HPPMy,
在Rt△PCH中,CHy,
∴BC=2CHy,
∴AD=BCy,
在Rt△APD中,APy,
∵BG∥AP,
∴△BMG∽△AMP,
∴,
∴BGy,
∴,
∴ABBG.
2.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠ABE=∠DAF,
∴∠AOE=∠BAF+∠ABE=∠BAF+∠DAF=∠BAD=90°,
∴AF⊥BE.
(2)解:如图1,延长AF交CD于点G,
∵GD∥AB,
∴△GDF∽△ABF,
∵DFBF,AB=2,AD=3,
∴,
∴GDAB2=1,
∵∠BAE=∠ADG=90°,∠ABE=∠DAG,
∴tan∠ABE=tan∠DAG,
∴AEAB2,
∴DE=AD﹣AE=3,
∴DE的长是.
(3)解:如图2,延长AF交CD于点H,
∵四边形ABCD是正方形,
∴AB=AD,∠ADH=90°,
设AB=AD=2m,
∵HD∥AB,
∴△HDF∽△ABF,
∵DFBF,
∴,
∴HDAB2m=m,
∴AHm,
∴AFAHAHmm,
∴,
∴的值为.
3.【解答】(1)证明:延长DE和CB交于点G,
∵AD∥BC,
∴,
∵AEAB,DF
∴,,
∴,
∴EF∥BC.
(2)①记点O为△ADE外接圆圆心,过点O作OF⊥AE于点F,连接OA,OD,OE.
∵点O为△ADE外接圆的圆心,
∴OA=OE=OD,
∴AF=EFAE,
∵AEAB,
∴AB=3AE=3,
∵AE=AD,OE=OD,OA=OA,
∴△AOE≌△AOD(SSS),
∴∠EAO=∠DAO,
∵BO平分∠ABC,
∴∠ABO=∠CBO,
∵AD∥BC,
∴∠DAB+∠ABC=180°,
∴2∠EAO+2∠ABO=180°,即∠EAO+∠ABO=90°,
∴∠AOB=90°,
∵OF⊥AE,
∴∠AFO=∠AOB=90°,
∵∠FAO=∠OAB,
∴△FAO∽△OAB,
∴,即AO2=AF AB,
∴AO,
∴△ADE外接圆半径为.
②方法一:延长BA,CD交于点P,过点E作EQ⊥BC,垂足为点Q.
∵AD∥BC,
∴△PAD∽△PBC,
∴,
由①知AB=3,
∴,
∴PA=1,
∵CD2=DM DN,
∴,
∵∠CDN=∠MDC,
∴△DCN∽△DMC,
∴∠DCN=∠CMD,
∵∠DMC=∠CEM,
∴∠CEM=∠DCN,
∴EM∥CD,
∴,
由AB=3,AE=1得,BE=2,
∴,
∴BM=MC=2,
∴△BEM∽△BPC,
∴,
设ME=2a,则PC=4a,
∵AD∥BC,
∴,
∴PD=a,DC=3a,
∵EM∥CD,
∴△ENM∽△CND,
∴,
设EN=2b,则CN=3b,
∵∠DMC=∠CEM,∠ECM=∠MCN,
∴△CNM∽△CME,
∴,即CM2=CN CE,
∴4=3b 5b,解得b,
∴CE,
在Rt△BQE中,由勾股定理可得:
BE2﹣BQ2=CE2﹣CQ2,
∴4﹣BQ2=()2﹣(4﹣BQ)2,
解得BQ,
∴EQ2=BE2﹣BQ2,
∵QM=BM﹣BQ=2,
∴在Rt△EQM中,由勾股定理可得,EM,
∵,
∴DC.
方法二:
∵AD=AE=1,
∴AB=3AE=3,
∵AD∥BC,BC=4,
∴,即,
∴AP=1=AD=AE,
∵BE=AP﹣AE=2,PE=AE+AP=2,
∴E为BP中点,
∵CD2=DM DN,
∴△DCN∽△DMC,
∴∠DCN=∠DMC=∠CEM,
∴EM∥CD,
∴M也为BC中点,
∴CM=BM=2,
∵BP=BC=4,
∴∠P=∠DCM,
∵∠ECP=∠DMC,
∴△ECP∽△DMC,
∴,
设DP=a,则CD=3a,CP=4a,
∴,解得a,
∴CD.
方法三:由CD2=DM DN易得△DCN∽△DMC,
∴∠DCN=∠CMD,
∵∠DMC=∠CEM,
∴∠CEM=∠DCN,
∴EM∥CD,
延长DA、ME交于点F,
则四边形CDFM是平行四边形,
∴△EAF∽△EBM,
∴,
设AF=n,则BM=2n,DF=CM=n+1,
∴BC=BM+CM=2n+n+1=4,
解得n=1,
∴AF=1,BM=2,
连接DE,
由AD=AF=AE可得∠DEF=90°,
设EF=m,则EM=2m,CD=3m,设EN=2t,则CN=3t,
由△CMN∽△CEM可得,
,即CM2=CE CN,
∴4=3t 5t,
解得t2,
由DE2=DF2﹣EF2=CE2﹣CD2得,
22﹣m2=25t2﹣9m2,
解得m,
∴CD=3m.
4.【解答】(1)解:如图1,设DE与CF交于点G,
∵四边形ABCD是正方形,
∴∠A=∠FDC=90°,AD=CD,
∵DE⊥CF,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,
∴∠CFD=∠AED,
在△AED和△DFC中,
,
∴△AED≌△DFC(AAS),
∴DE=CF,
∴1;
(2)解:如图2,设DB与CE交于点G,
∵四边形ABCD是矩形,
∴∠A=∠EDC=∠BCD=90°,
∵∠DBC=30°,
∴∠CDG=60°,
∵CE⊥BD,
∴∠DGC=90°,
∴∠DCE=30°,
∴CECD,BD=2CD,
∴;
(3)证明:如图3,过点C作CH⊥AF交AF的延长线于点H,
∵CG⊥EG,
∴∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,
∴△DEA∽△CFH,
∴,
∴,
∴DE AB=CF AD.
5.【解答】(1)证明:∵ ABCD,
∴AD∥BC,OA=OC,
∴AM∥CN,
∵AM=CN,
∴四边形AMCN是平行四边形,
∴AN∥CM,
∴∠OAE=∠OCF,
在△AOE与△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF;
(2)(i)证明:∵HE∥AB,
∴,
∵OB=OD,OE=OF,
∴,
∵∠HOF=∠AOD,
∴△HOF∽△AOD,
∴∠OHF=∠OAD,
∴HF∥AD;
(ii)解:∵ ABCD为菱形,
∴AC⊥BD,
∵OE=OF,∠EHF=60°,
∴∠EHO=∠FHO=30°,
∴,
∵AM∥BC,MD=2AM,
∴,即HC=3AH,
∴OA+OH=3(OA﹣OH),
∴OA=2OH,
∵BN∥AD,MD=2AM,AM=CN,
∴,即3BE=2ED,
∴3(OB﹣OE)=2(OB+OE),
∴OB=5OE,
∴,
∴的值是.
6.【解答】(1)证明:∵∠BAD=∠C,∠ABD=∠CBA,
∴△ABD∽△CBA,
∴,
∴AB2=BD BC;
(2)解:过点C作CF⊥AB于点F,过点D作DG⊥AB于点G,
则∠AFC=∠AGD=90°,
∴CF∥DG,∠BAC=60°,
∴,,
∵D为BC的中点,
∴,
∵CF∥DG,
∴△BDG∽△BCF,
∴,
∴,
∴,
∴,
∴,
∵AC=CD,
∴∠CAD=∠CDA,
∵∠AED=∠CAD,
∴∠AED=∠CDA,
∴∠AED+∠BED=∠ADC+∠ADB=180°,
∴∠BED=∠ADB,
∵∠DBE=∠ABD,
∴△BED∽△BDA,
∴,即,
解得:;
(3)解:连接BD,
∵四边形ABCD为菱形,
∴,AD=AB=BC=5,AD∥BC,
∵∠ABC=2∠EBF,
∴∠ABD=∠CBD=∠EBF,
∴∠EBF﹣∠DBF=∠CBD﹣∠DBF,即∠DBE=∠CBF,
∵AD∥BC,
∴∠CBF=∠G,
∴∠DBE=∠G,
∵∠DEB=∠BEG,
∴△BED∽△GEB,
∴,
∵DG=6,
∴EG=DE+6,
∴,
解得:DE=2,负值舍去,
∴EG=2+6=8,
∴AE=AD﹣DE=3,
∵AE2+BE2=32+42=52=AB2,
∴△ABE为直角三角形,∠AEB=90°,
∴∠BEG=180°﹣90°=90°,
∴在Rt△BEG中根据勾股定理得:,
∴,
∵AD∥BC,
∴△DFG∽△CFB,
∴,
即,
解得:.
7.【解答】(1)证明:∵正方形ABCD,
∴∠B=90°,
∵FG⊥BC,
∴∠G=90°,
由∠B=∠G,∠1=∠2,AE=EF,
得△ABE≌△EGF(AAS);
(2)①证明:连BP.
由(1)得△ABE≌△EGF,
∴∠AEB=∠EFG,
∴∠AEB+∠GEF=∠AEB+∠BAE=90°,
即∠AEF=90°,
∴△AEF是等腰直角三角形,
∵EM⊥AF,
∴∠APE=90°,∠AEP=∠FEP=45°,
∵∠ABE=90°,
∴A、B、E、P四点共圆,
∴∠ABP=∠AEP=45°,
∵∠ABE=90°,∠ABP=∠CBP=45°,
∴点
P
在∠ABC的平分线上;
②m+1.
理由如下:
由①得点
P
在∠ABC的平分线即正方形的对角线上,如图:
∵正方形ABCD,
∴AB∥HD,
∴△ABP∽△HDP,
∴,
∵m,
∴HC=mHD,
∴DC=DH+HC=(m+1)HD,
∴m+1;
③由①得点
P
在∠ABC的平分线即正方形的对角线上,
∴∠PDH=45°,
同理M、D、H、P四点共圆,
∴∠PMH=∠PDH=45°,
∵∠AEP=∠NEM=45°,
∴∠EMH=∠NEM=45°,
∴MH∥EN,
∵MN∥HE,
∴四边形MNEH是平行四边形,
∵△AEF是等腰直角三角形,
∴△PHQ和△PHM都是等腰直角三角形,
设PM=PH=a,则MQ=2a,ME=2MQ=4a,
∵PM=PH,PA=PE,
∴AH=ME=4a,
∴AP=3a,
则AE=3a,
∴BE,
∵∠APM=∠ADH,
∴△APM∽△ADH,
∴,
∴DH,
∴AH2,
∵AH=4a,
∴4a=2,
∴a,
∴BE3.
8.【解答】(1)证明:如图2,∵∠A=∠A,∠ACD=∠B,
∴△ACD∽△ABC,
∴,
∴AC2=AD AB.
(2)解:如图3,设AD=m,
∵点D为AB中点,
∴AD=BD=m,AB=2m,
由(1)得△ACD∽△ABC,
∴,
∴AC2=AD AB=m×2m=2m2,
∴ACm或ACm(不符合题意,舍去),
∴,
∵BC=4,
∴CDBC4=2,
∴CD的长是2.
(3)解法一:如图4,作BF⊥DC交DC的延长线于点F,则∠F=90°,
∵点E为CD中点,
∴CE=DE,
设CE=DE=n,
∵∠CDB=∠CBD=30°,
∴CB=CD=2n,∠BCF=∠CDB+∠CBD=60°,
∴∠FBC=90°﹣∠BCF=30°,
∴CFCB=n,
∴EF=CE+CF=2n,BFn,
∴BD=2BF=2n,BEn,
作CH∥EB交AB的延长线于点H,则△HDC∽△BDE,
∴2,
∴HC=2BE=2n,HD=2BD=4n,
∵∠ACD=∠EBD,∠H=∠EBD,
∴∠ACD=∠H,
∵∠A=∠A,
∴△ACD∽△AHC,
∴,
∵AC=2,
∴ADAC22,AHAC214,
∴HD=AH﹣AD=14﹣2=12,
∴4n=12,
解得n,
∴BE,
∴BE的长是.
解法二:如图5,取BD中点M,连接CM、EM,
∵点E为CD中点,
∴DM是△BCD的中位线,
∴EM∥CB,
∵∠CDB=∠CBD=30°,
∴CD=CB,∠EMD=∠CBD=30°,
∴CM⊥BD,∠ADC=∠BME=180°﹣30°=150°,
∵∠ACD=∠EBD,即∠ACD=∠EBM,
∴△ACD∽△EBM,
∵∠CMB=90°,∠CBM=30°,AC=2,
∴CD=CB=2CM,
设CM=x,则CD=CB=2x,
∴BMx,
∴,
∴BEAC2,
∴BE的长是.
9.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠PAE=∠QCE=45°,
∵CE=2AE,AP=t,CQ=2t,
∴,
∴△AEP∽△CEQ;
(2)解:方法一:过点E作EM⊥AB于点M,过点E作 EN⊥BC于点N.
由题意知AE,AM=ME=2,EN=CN=4,AP=t,
CQ=2t,BQ=6﹣2t,MP=|t﹣2|,BP=6﹣t,QN=|2t﹣4|,
∴EP2=EM2+MP2,即EP2=22+(2﹣t)2=t2﹣4t+8,
PQ2=BP2+BQ2,即PQ2=(6﹣t)2+(6﹣2t)2=5t2﹣36t+72,
EQ2=EN2+NQ2,即EQ2=42+(2t﹣4)2=4t2﹣16t+32,
①当∠EPQ=90°时,则EQ2=EP2+PQ2,
即4t2﹣16t+32=t2﹣4t+8+5t2﹣36t+72,
整理得t2﹣12t+24=0.
解得t1=6,t2=6(不合题意,舍去),
②当∠PEQ=90°时,则PQ2=EP2+EQ2,
即5t2﹣36t+72=t2﹣4t+8+4t2﹣16t+32,
整理得t﹣2=0,
解得t=2;
③当∠PQE=90°时,则EP2=PQ2+EQ2,
即t2﹣4t+8=5t2﹣36t+72+4t2﹣16t+32,
整理得t2﹣6t+12=0,该方程无实数解,
综上所述,当△EPQ是直角三角形时,t的值为秒或2秒;
(3)解:方法一:过点A作AF⊥AC,交CB的延长线于点F,连接FE交AQ于点G.如图2,
∵AF⊥AC,∠ACF=45°,
∴AF=AC,
又∵CE=2AE,
∴,
∴tan∠AFE,
∵tan∠AQE,
∴∠AFE=∠AQE,
∵∠AGF=∠EGQ,
∴△AGF∽△EGQ,
∴,
∵∠AGE=∠FGQ,
∴△AGE∽△FGQ,
∴∠AEG=∠FQG,
∵∠AFE+∠AEF=90°,
∴∠FQG+∠EQG=90°,即∠FQE=90°,
∴AB∥EQ,△EQC是等腰直角三角形,
∴,即,
∴QC=QE=4,
∴S△AEQ=S△AQC﹣S△EQC
QC ABQC EQ
4×64×4
=4(cm2).
方法二:∵AF⊥AC,∠ACF=45°,
∴AF=AC,
又∵CE=2AE,
∴,
∴tan∠AFE,
∵tan∠AQE,
∴∠AFE=∠AQE,
∴A,F,Q,E四点共圆,直径为EF,如图3,
∴∠FQE=90°,
∴AB∥EQ,△EQC是等腰直角三角形,
∴,即,
∴QC=QE=4,
∴S△AEQ=S△AQC﹣S△EQC
QC ABQC EQ
4×64×4
=4(cm2).
10.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠C=∠ADE=90°,
∴∠CDF+∠DFC=90°,
∵AE⊥DF,
∴∠DGE=90°,
∴∠CDF+∠AED=90°,
∴∠AED=∠DFC,
∴△ADE∽△DCF;
(2)证明:∵四边形ABCD是正方形,
∴AD=DC,AD∥BC,∠ADE=∠DCF=90°,
∵AE=DF,
∴Rt△ADE≌Rt△DCF(HL),
∴DE=CF,
∵CH=DE,
∴CF=CH,
∵点H在BC的延长线上,
∴∠DCH=∠DCF=90°,
又∵DC=DC,
∴△DCF≌△DCH(SAS),
∴∠DFC=∠H,
∵AD∥BC,
∴∠ADF=∠DFC,
∴∠ADF=∠H;
(3)解:如图3,延长BC至点G,使CG=DE=8,连接DG,
∵四边形ABCD是菱形,
∴AD=DC,AD∥BC,
∴∠ADE=∠DCG,
∴△ADE≌△DCG(SAS),
∴∠DGC=∠AED=60°,AE=DG,
∵AE=DF,
∴DG=DF,
∴△DFG是等边三角形,
∴FG=DF=11,
∵CF+CG=FG,
∴CF=FG﹣CG=11﹣8=3,
即CF的长为3.
11.【解答】(1)①证明:如图1中,∵四边形ABCD是正方形,
∴∠A=∠D=90°,
∵∠CEF=90°,
∴∠AEF+∠CED=90°,∠ECD+∠CED=90°,
∴∠AEF=∠ECD,
∴△AEF∽△DCE;
②解:如图2中,延长DA交CF的延长线于点G,过点G作GH⊥CE交CE的延长线于点H.
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴,
∵CD=2,AE=ED=1,
∴GH=2HE,
设EH=m,GH=2m.
∵CE,
∴CH=m,
∵tan∠ECF,
∴,
∴m,
∴EH,GH,
∴EG,
∴AG=EG﹣AE1,DG=EG+DE1,
∵AF∥CD,
∴,
∴,
∴AF;
(3)证明:如图3中,过点G作GH⊥CE交CE的延长线于点H.
设AD=CD=a,GE=DE=t,EH=x,GH=y,CE=n,
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴
∴,
∴x,y,
在Rt△CGH中,sin∠ECF,
∴CG=3GH,CH=2GH,
∴,
∴2y=x+n,
∴2n,
∴2at=t2+n2,
在Rt△CDE中,n2=t2+a2,
∴2at=2t2+a2,
∴at,
∵AF∥CD,
∴,
∴,
∴AFaa﹣t,
∵AE=a﹣t,
∴AE=AF.
解法二:设AE=x,则DE=EG=1﹣x,DG=2﹣2x,
∴S△CDE=S△CEG,
∴(1﹣x)×1 ,
解得x=1(负根已经舍去),
∴AE=1,
由AF:CD=AG:DG,可得AF:1=(1):,
∴AF=1.
∴AE=AF.
12.【解答】(1)证明:∵∠A+∠AGA'=90°,∠A'+∠AGA'=90°,
∴∠A=∠A',
∵AD=A'D,∠ADE=∠A'DG=90°,
∴△ADE≌△A′DG(ASA);
(2)证明:∵∠AFG=∠ACB=90°,∠FAG=∠CAB,
∴△AFG∽△ACB,
∴,
∴,
∵∠FAC=∠GAB,
∴△FAC∽△GAB,
∴,
∴AF GB=AG FC;
(3)解:∵tanA,AC=8,
∴BC=4,
∴S△ACB=16,
设DE=DG=x,则AD=A'D=2x,AE=A'Gx,
∴A'E=A'D﹣DE=2x﹣x=x,
∴S△ADE=S△A′DG=x2,
∵△A'FE∽△A'DG,
∴,
∴S△A'FE:S△A'DG=1:5,
∴S四边形DGFES△A'DGx2,
∵S△ACB=S△ADE+S四边形DCBE,A′G平分四边形DCBE的面积,
∴S△ACB=S△ADE+2S四边形DGFE,
∴16=x2x2,
x2
∴x1,x2(舍),
∴AD.
13.【解答】解:(1)如图1,连接OD,
∵CD切半圆O于点D,
∴OD⊥CE,
∵OA,AC=1,
∴OC,BC=4,
∴CD2,
∵BE⊥CE,
∴OD∥BE,
∴,
∴,
∴CE,
如图2,∵∠AFB=∠E=90°,
∴AF∥CE,
∴MN∥CB,
∴四边形APMC是平行四边形,
∴CM=PAx,
∵NM∥BC,
∴△BCE∽△NME,
∴,
∴,
∴yx+4;
(2)∵PN=y﹣1x+4﹣1x+3,PH<PN,△BCE的三边之比为3:4:5,
∴可分为三种情况,
当PH:PN=3:5时,xx+3,解得:x,
∴ax,
当PH:PN=4:5时,xx+3,解得:x,
∴ax,
当PH:PN=3:4时,xx+3,解得:x,
∴ax,
综上所述:a的值为或或;
(3)如图3,连接AQ,BQ,过点Q作QG⊥AB于点G,
则∠AQB=∠AGQ=90°,PH=QG=x,
∴∠QAB=∠BQG,
∵NQx﹣3,PN=y﹣1x+3,
∴HG=PQ=NQ+PNx,
∵AHx,
∴AG=AH+HG=3x,
∴tan∠BQG=tan∠QAB,
∴BGQGx,
∴AB=AG+BGx=3,
∴x,
∴yx+4,
∴MN的长为.
14.【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD=CB=CD,∠ABC=∠ADC=90°,
∴∠BAC=∠BCA=∠DAC=∠DCA=45°,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS).
(2)解:△FBG是等腰三角形,理由如下:
∵△ABE≌△ADE,
∴∠ABE=∠ADE,
∴∠ABC﹣∠ABE=∠ADC﹣∠ADE,
∴∠EBC=∠EDC,
∵AB∥CD,
∴∠FGB=∠EDC,
∴∠FGB=∠EBC,
∵BF⊥BE,
∴∠FBE=90°,
∴∠FBG=∠EBC=90°﹣∠ABE,
∴∠FGB=∠FBG,
∴BF=GF,
∴△FBG是等腰三角形.
(3)解:∵BE=BF=2,∠FBE=90°,
∴∠F=∠BEF=45°,
∴∠BAC=∠F,
∴∠AEG=∠AGF﹣∠BAC=∠AGF﹣∠F=∠FBG,
∵∠AGE=∠FGB,且∠FGB=∠FBG,
∴∠AGE=∠AEG,
∴AE=AG,
∵EF2,BF=GF=2,
∴GE=EF﹣GF=22,
∵△ABE≌△ADE,
∴BE=DE=2,
∵AG∥CD,
∴△AGE∽△CDE,
∴1,
∴1,
∴的值为1.
15.【解答】(1)证明:∵EF⊥AB,AM是BC边上的高,
∴∠AMB=∠EFB=90°,
又∵∠B=∠B,
∴△ABM∽△EBF;
(2)解:过点E作EN⊥AD于点N,如图:
在平行四边形ABCD中,AD∥BC,
又∵AM是BC边上的高,
∴AM⊥AD,
∴∠AME=∠MAN=∠ANE=90°,
∴四边形AMEN为矩形,
∴NE=AM=4,AN=ME,
在Rt△ABM中,,
又∵E为BC的中点,
∴,
∴ME=AN=2,
∴DN=8,
在Rt△DNE中,;
(3)解:延长FE交DC的延长线于点G,如图:
∵sinB,
∴,
∴EFx,
∵AB∥CD,
∴∠B=∠ECG,∠EGC=∠BFE=90°,
又∵∠AMB=∠EGC=90°,
∴△ABM∽△ECG,
∴,
∴,
∴GC(10﹣x),
∴DG=DC+GC=5(10﹣x),
∴yEF DGx [5(10﹣x)]x2x(x)2,
∴当x时,y有最大值为,
答:yx2x,当x时,y有最大值为.
16.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠CED+∠DCE=90°,
∵EF⊥CE,
∴∠CED+∠AEF=90°,
∴∠DCE=∠AEF,
∴△AEF∽△DCE;
(2)解:①连接AM,如图2,
∵BG⊥CF,
∴△BGC是直角三角形,
∵点M是BC的中点,
∴MB=CM=GM,
∴点G在以点M为圆心,3为半径的圆上,
当A,G,M三点不共线时,由三角形两边之和大于第三边得:AG+GM>AM,
当A,G,M三点共线时,AG+GM=AM,
此时,AG+GM取得最小值,
在Rt△ABM中,AM5,
∴AG+GM的最小值为5.
②方法一:
如图3,过点M作MN∥AB交FC于点N,
∴△CMN∽△CBF,
∴,
设AF=x,则BF=4﹣x,
∴MNBF(4﹣x),
∵MN∥AB,
∴△AFG∽△MNG,
∴,
由(2)可知AG+GM的最小值为5,
即AM=5,
又∵GM=3,
∴AG=2,
∴,
解得x=1,
即AF=1,
由(1)得,
设DE=y,则AE=6﹣y,
∴,
解得:y=3或y=3,
∵06,0<36,
∴DE=3或DE=3.
方法二:
如图4,过点G作GH∥AB交BC于点H,
∴△MHG∽△MBA,
∴,
由(2)可知AG+MG的最小值为5,
即AM=5,
又∵GM=3,
∴,
∴GH,MH,
由GH∥AB得△CHG∽△CBF,
∴,
即,
解得FB=3,
∴AF=AB﹣FB=1.
由(1)得,
设DE=y,则AE=6﹣y,
∴,
解得:y=3或y=3,
∵06,0<36,
∴DE=3或DE=3.
17.【解答】(1)①证明:如图1,
∵AD=CD,
∴∠DAC=∠DCA.
∵AD∥BC,
∴∠DAC=∠ACB.
∵BO是Rt△ABC斜边AC上的中线,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠DAC=∠DCA=∠ACB=∠OBC,
∴△DAC∽△OBC;
②解:如图2,若BE⊥CD,
在Rt△BCE中,∠OCE=∠OCB=∠EBC,
∴∠OCE=∠OCB=∠EBC=30°.
过点D作DH⊥BC于点H,
设AD=CD=2m,则BH=AD=2m,
在Rt△DCH中,DC=2m,
∴CH=m,
∴BC=BH+CH=3m,
∴;
(2)①如图3,当点E在AD上时,
∵AD∥BC,
∴∠EAO=∠BCO,∠AEO=∠CBO,
∵O是AC的中点,
∴OA=OC,
∴△AOE≌△COB(AAS),
∴OB=OE,
∴四边形ABCE是平行四边形,
又∵∠ABC=90°,
∴四边形ABCE是矩形.
设AD=CD=x,
∵DE=2,
∴AE=x﹣2,
∵OE=3,
∴AC=6,
在Rt△ACE和Rt△DCE中,CE2=AC2﹣AE2,CE2=CD2﹣DE2,
∴62﹣(x﹣2)2=x2﹣22,
解得x=1,或x=1(舍去).
∴CD=1.
②如图4,当点E在CD上时,设AD=CD=x,则CE=x﹣2,
设OB=OC=m,
∵OE=3,
∴EB=m+3,
∵△DAC∽△OBC,
∴,
∴,
∴.
又∵∠EBC=∠OCE,∠BEC=∠OEC,
∴△EOC∽△ECB,
∴,
∴,
∴,
∴m,
将m代入,
整理得,x2﹣6x﹣10=0,
解得x=3,或x=3(舍去).
∴CD=3.
综合以上可得CD的长为1或3.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练相似形综合压轴题训练
1.在矩形ABCD中,点E,F分别在边AD,BC上,将矩形ABCD沿EF折叠,使点A的对应点P落在边CD上,点B的对应点为点G,PG交BC于点H.
(1)如图1,求证:△DEP∽△CPH;
(2)如图2,当P为CD的中点,AB=2,AD=3时,求GH的长;
(3)如图3,连接BG,当P,H分别为CD,BC的中点时,探究BG与AB的数量关系,并说明理由.
2.如图1,在矩形ABCD中,点E为AD边上不与端点重合的一动点,点F是对角线BD上一点,连接BE,AF交于点O,且∠ABE=∠DAF.
【模型建立】
(1)求证:AF⊥BE;
【模型应用】
(2)若AB=2,AD=3,DFBF,求DE的长;
【模型迁移】
(3)如图2,若矩形ABCD是正方形,DFBF,求的值.
3.在梯形ABCD中,AD∥BC,点E在边AB上,且.
(1)如图1所示,点F在边CD上,且,联结EF,求证:EF∥BC;
(2)已知AD=AE=1;
①如图2所示,联结DE,如果△ADE外接圆的圆心恰好落在∠B的平分线上,求△ADE的外接圆的半径长;
②如图3所示,如果点M在边BC上,联结EM、DM、EC,DM与EC交于N.如果∠DMC=∠CEM,BC=4,且CD2=DM DN,求边CD的长.
4.某学校数学兴趣小组在数学课外活动中,对多边形内两条互相垂直的线段做了如下探究:
(1)如图1,在正方形ABCD中,点E,F分别是AB,AD上的两点,连接DE,CF,且DE⊥CF,猜想并计算的值;
(2)如图2,在矩形ABCD中,∠DBC=30°,点E是AD上的一点,连接CE,BD,且CE⊥BD,求的值;
(3)如图3,在四边形ABCD中,∠A=∠B=90°,点E为AB上一点,连接DE,过点C作DE的垂线交ED的延长线于点G,交AD的延长线于点F,求证:DE AB=CF AD.
5.如图1, ABCD的对角线AC与BD交于点O,点M,N分别在边AD,BC上,且AM=CN.点E,F分别是BD与AN,CM的交点.
(1)求证:OE=OF;
(2)连接BM交AC于点H,连接HE,HF.
(ⅰ)如图2,若HE∥AB,求证:HF∥AD;
(ⅱ)如图3,若 ABCD为菱形,且MD=2AM,∠EHF=60°,求的值.
6.(1)【观察发现】如图1,在△ABC中,点D在边BC上.若∠BAD=∠C,则AB2=BD BC,请证明;
(2)【灵活运用】如图2,在△ABC中,∠BAC=60°,点D为边BC的中点,CA=CD=2,点E在AB上,连接AD,DE.若∠AED=∠CAD,求BE的长;
(3)【拓展延伸】如图3,在菱形ABCD中,AB=5,点E,F分别在边AD,CD上,∠ABC=2∠EBF,延长AD,BF相交于点G.若BE=4,DG=6,求FG的长.
7.正方形ABCD中,点E是边BC上的动点(不与点B、C重合),∠1=∠2,AE=EF,AF交CD于点H,FG⊥BC交BC延长线于点G.
(1)如图1,求证:△ABE≌△EGF;
(2)如图2,EM⊥AF于点P,交AD于点M.
①求证:点P在∠ABC的平分线上;
②当时,猜想AP与PH的数量关系,并证明;
③作HN⊥AE于点N,连接MN、HE,当MN∥HE时,若AB=6,求BE的值.
8.数学实验,能增加学习数学的乐趣,还能经历知识“再创造”的过程,更是培养动手能力,创新能力的一种手段.小强在学习《相似》一章中对“直角三角形斜边上作高”这一基本图形(如图1)产生了如下问题,请同学们帮他解决.
在△ABC中,点D为边AB上一点,连接CD.
(1)初步探究
如图2,若∠ACD=∠B,求证:AC2=AD AB;
(2)尝试应用
如图3,在(1)的条件下,若点D为AB中点,BC=4,求CD的长;
(3)创新提升
如图4,点E为CD中点,连接BE,若∠CDB=∠CBD=30°,∠ACD=∠EBD,AC=2,求BE的长.
9.如图,正方形ABCD边长为6cm,点E为对角线AC上一点,CE=2AE,点P在AB边上以1cm/s的速度由点A向点B运动,同时点Q在BC边上以2cm/s的速度由点C向点B运动,设运动时间为t秒(0<t≤3).
(1)求证:△AEP∽△CEQ.
(2)当△EPQ是直角三角形时,求t的值.
(3)连接AQ,当tan∠AQE时,求△AEQ的面积.
10.(1)如图1,在矩形ABCD中,点E,F分别在边DC,BC上,AE⊥DF,垂足为点G.求证:△ADE∽△DCF.
【问题解决】
(2)如图2,在正方形ABCD中,点E,F分别在边DC,BC上,AE=DF,延长BC到点H,使CH=DE,连接DH.求证:∠ADF=∠H.
【类比迁移】
(3)如图3,在菱形ABCD中,点E,F分别在边DC,BC上,AE=DF=11,DE=8,∠AED=60°,求CF的长.
11.如图,在正方形ABCD中,E,F分别是边AD,AB上的点,连接CE,EF,CF.
(1)若正方形ABCD的边长为2,E是AD的中点.
①如图1,当∠FEC=90°时,求证:△AEF∽△DCE;
②如图2,当tan∠FCE时,求AF的长;
(2)如图3,延长CF,DA交于点G,当GE=DE,sin∠FCE时,求证:AE=AF.
12.如图,在Rt△ABC中,∠ACB=90°,AC>BC,点D在边AC上,将线段DA绕点D按顺时针方向旋转90°得到DA′,线段DA′交AB于点E,作A′F⊥AB于点F,与线段AC交于点G,连接FC,GB.
(1)求证:△ADE≌△A′DG;
(2)求证:AF GB=AG FC;
(3)若AC=8,tanA,当A′G平分四边形DCBE的面积时,求AD的长.
13.如图1,AB为半圆O的直径,C为BA延长线上一点,CD切半圆于点D,BE⊥CD,交CD延长线于点E,交半圆于点F,已知OA,AC=1.如图2,连结AF,P为线段AF上一点,过点P作BC的平行线分别交CE,BE于点M,N,过点P作PH⊥AB于点H.设PH=x,MN=y.
(1)求CE的长和y关于x的函数表达式;
(2)当PH<PN,且长度分别等于PH,PN,a的三条线段组成的三角形与△BCE相似时,求a的值;
(3)延长PN交半圆O于点Q,当NQx﹣3时,求MN的长.
14.已知正方形ABCD,E是对角线AC上一点.
(1)如图1,连接BE,DE.求证:△ABE≌△ADE;
(2)如图2,F是DE延长线上一点,DF交AB于点G,BF⊥BE.判断△FBG的形状并说明理由;
(3)在第(2)题的条件下,BE=BF=2.求的值.
15.如图,平行四边形ABCD中,AB=5,BC=10,BC边上的高AM=4,点E为BC边上的动点(不与B、C重合,过点E作直线AB的垂线,垂足为F,连接DE、DF.
(1)求证:△ABM∽△EBF;
(2)当点E为BC的中点时,求DE的长;
(3)设BE=x,△DEF的面积为y,求y与x之间的函数关系式,并求当x为何值时,y有最大值,最大值是多少?
16.如图1,在矩形ABCD中,AB=4,BC=6.点E是线段AD上的动点(点E不与点A,D重合),连接CE,过点E作EF⊥CE,交AB于点F.
(1)求证:△AEF∽△DCE;
(2)如图2,连接CF,过点B作BG⊥CF,垂足为G,连接AG.点M是线段BC的中点,连接GM.
①求AG+GM的最小值;
②当AG+GM取最小值时,求线段DE的长.
17.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AD=CD,O是对角线AC的中点,联结BO并延长交边CD或边AD于点E.
(1)当点E在CD上,
①求证:△DAC∽△OBC;
②若BE⊥CD,求的值;
(2)若DE=2,OE=3,求CD的长.
参考答案
1.【解答】(1)证明:如图,
∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°,
∴∠1+∠3=90°,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在DC上,
∴∠EPH=∠A=90°,
∴∠1+∠2=90°,
∴∠3=∠2,
∴△EDP∽△PCH;
(2)解:∵四边形ABCD是矩形,
∴CD=AB=2,AD=BC=3,∠A=∠D=∠C=90°,
∵P为CD中点,
∴DP=CP1,
设EP=AE=x,
∴ED=AD﹣x=3﹣x,
在Rt△EDP中,EP2=ED2+DP2,
即x2=(3﹣x)2+1,
解得x,
∴EP=AP=x,
∴ED=AD﹣AE,
∵△EDP∽△PCH,
∴,即,
∴PH,
∵PG=AB=2,
∴GH=PG﹣PH.
(3)解:如图,延长AB,PG交于一点M,连接AP,
∵E,F分别在AD,BC上,将四边形ABFE沿EF翻折,使A的对称点P落在CD上,
∴AP⊥EF,BG⊥直线EF,
∴BG∥AP,
∵AE=EP,
∴∠EAP=∠EPA,
∴∠BAP=∠GPA,
∴△MAP是等腰三角形,
∴MA=MP,
∵P为CD中点,
∴设DP=CP=y,
∴AB=PG=CD=2y,
∵H为BC中点,
∴BH=CH,
∵∠BHM=∠CHP,∠CBM=∠PCH,
∴△MBH≌△PCH(ASA),
∴BM=CP=y,HM=HP,
∴MP=MA=MB+AB=3y,
∴HPPMy,
在Rt△PCH中,CHy,
∴BC=2CHy,
∴AD=BCy,
在Rt△APD中,APy,
∵BG∥AP,
∴△BMG∽△AMP,
∴,
∴BGy,
∴,
∴ABBG.
2.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠BAD=90°,
∵∠ABE=∠DAF,
∴∠AOE=∠BAF+∠ABE=∠BAF+∠DAF=∠BAD=90°,
∴AF⊥BE.
(2)解:如图1,延长AF交CD于点G,
∵GD∥AB,
∴△GDF∽△ABF,
∵DFBF,AB=2,AD=3,
∴,
∴GDAB2=1,
∵∠BAE=∠ADG=90°,∠ABE=∠DAG,
∴tan∠ABE=tan∠DAG,
∴AEAB2,
∴DE=AD﹣AE=3,
∴DE的长是.
(3)解:如图2,延长AF交CD于点H,
∵四边形ABCD是正方形,
∴AB=AD,∠ADH=90°,
设AB=AD=2m,
∵HD∥AB,
∴△HDF∽△ABF,
∵DFBF,
∴,
∴HDAB2m=m,
∴AHm,
∴AFAHAHmm,
∴,
∴的值为.
3.【解答】(1)证明:延长DE和CB交于点G,
∵AD∥BC,
∴,
∵AEAB,DF
∴,,
∴,
∴EF∥BC.
(2)①记点O为△ADE外接圆圆心,过点O作OF⊥AE于点F,连接OA,OD,OE.
∵点O为△ADE外接圆的圆心,
∴OA=OE=OD,
∴AF=EFAE,
∵AEAB,
∴AB=3AE=3,
∵AE=AD,OE=OD,OA=OA,
∴△AOE≌△AOD(SSS),
∴∠EAO=∠DAO,
∵BO平分∠ABC,
∴∠ABO=∠CBO,
∵AD∥BC,
∴∠DAB+∠ABC=180°,
∴2∠EAO+2∠ABO=180°,即∠EAO+∠ABO=90°,
∴∠AOB=90°,
∵OF⊥AE,
∴∠AFO=∠AOB=90°,
∵∠FAO=∠OAB,
∴△FAO∽△OAB,
∴,即AO2=AF AB,
∴AO,
∴△ADE外接圆半径为.
②方法一:延长BA,CD交于点P,过点E作EQ⊥BC,垂足为点Q.
∵AD∥BC,
∴△PAD∽△PBC,
∴,
由①知AB=3,
∴,
∴PA=1,
∵CD2=DM DN,
∴,
∵∠CDN=∠MDC,
∴△DCN∽△DMC,
∴∠DCN=∠CMD,
∵∠DMC=∠CEM,
∴∠CEM=∠DCN,
∴EM∥CD,
∴,
由AB=3,AE=1得,BE=2,
∴,
∴BM=MC=2,
∴△BEM∽△BPC,
∴,
设ME=2a,则PC=4a,
∵AD∥BC,
∴,
∴PD=a,DC=3a,
∵EM∥CD,
∴△ENM∽△CND,
∴,
设EN=2b,则CN=3b,
∵∠DMC=∠CEM,∠ECM=∠MCN,
∴△CNM∽△CME,
∴,即CM2=CN CE,
∴4=3b 5b,解得b,
∴CE,
在Rt△BQE中,由勾股定理可得:
BE2﹣BQ2=CE2﹣CQ2,
∴4﹣BQ2=()2﹣(4﹣BQ)2,
解得BQ,
∴EQ2=BE2﹣BQ2,
∵QM=BM﹣BQ=2,
∴在Rt△EQM中,由勾股定理可得,EM,
∵,
∴DC.
方法二:
∵AD=AE=1,
∴AB=3AE=3,
∵AD∥BC,BC=4,
∴,即,
∴AP=1=AD=AE,
∵BE=AP﹣AE=2,PE=AE+AP=2,
∴E为BP中点,
∵CD2=DM DN,
∴△DCN∽△DMC,
∴∠DCN=∠DMC=∠CEM,
∴EM∥CD,
∴M也为BC中点,
∴CM=BM=2,
∵BP=BC=4,
∴∠P=∠DCM,
∵∠ECP=∠DMC,
∴△ECP∽△DMC,
∴,
设DP=a,则CD=3a,CP=4a,
∴,解得a,
∴CD.
方法三:由CD2=DM DN易得△DCN∽△DMC,
∴∠DCN=∠CMD,
∵∠DMC=∠CEM,
∴∠CEM=∠DCN,
∴EM∥CD,
延长DA、ME交于点F,
则四边形CDFM是平行四边形,
∴△EAF∽△EBM,
∴,
设AF=n,则BM=2n,DF=CM=n+1,
∴BC=BM+CM=2n+n+1=4,
解得n=1,
∴AF=1,BM=2,
连接DE,
由AD=AF=AE可得∠DEF=90°,
设EF=m,则EM=2m,CD=3m,设EN=2t,则CN=3t,
由△CMN∽△CEM可得,
,即CM2=CE CN,
∴4=3t 5t,
解得t2,
由DE2=DF2﹣EF2=CE2﹣CD2得,
22﹣m2=25t2﹣9m2,
解得m,
∴CD=3m.
4.【解答】(1)解:如图1,设DE与CF交于点G,
∵四边形ABCD是正方形,
∴∠A=∠FDC=90°,AD=CD,
∵DE⊥CF,
∴∠DGF=90°,
∴∠ADE+∠CFD=90°,∠ADE+∠AED=90°,
∴∠CFD=∠AED,
在△AED和△DFC中,
,
∴△AED≌△DFC(AAS),
∴DE=CF,
∴1;
(2)解:如图2,设DB与CE交于点G,
∵四边形ABCD是矩形,
∴∠A=∠EDC=∠BCD=90°,
∵∠DBC=30°,
∴∠CDG=60°,
∵CE⊥BD,
∴∠DGC=90°,
∴∠DCE=30°,
∴CECD,BD=2CD,
∴;
(3)证明:如图3,过点C作CH⊥AF交AF的延长线于点H,
∵CG⊥EG,
∴∠G=∠H=∠A=∠B=90°,
∴四边形ABCH为矩形,
∴AB=CH,∠FCH+∠CFH=∠DFG+∠FDG=90°,
∴∠FCH=∠FDG=∠ADE,∠A=∠H=90°,
∴△DEA∽△CFH,
∴,
∴,
∴DE AB=CF AD.
5.【解答】(1)证明:∵ ABCD,
∴AD∥BC,OA=OC,
∴AM∥CN,
∵AM=CN,
∴四边形AMCN是平行四边形,
∴AN∥CM,
∴∠OAE=∠OCF,
在△AOE与△COF中,
,
∴△AOE≌△COF(ASA),
∴OE=OF;
(2)(i)证明:∵HE∥AB,
∴,
∵OB=OD,OE=OF,
∴,
∵∠HOF=∠AOD,
∴△HOF∽△AOD,
∴∠OHF=∠OAD,
∴HF∥AD;
(ii)解:∵ ABCD为菱形,
∴AC⊥BD,
∵OE=OF,∠EHF=60°,
∴∠EHO=∠FHO=30°,
∴,
∵AM∥BC,MD=2AM,
∴,即HC=3AH,
∴OA+OH=3(OA﹣OH),
∴OA=2OH,
∵BN∥AD,MD=2AM,AM=CN,
∴,即3BE=2ED,
∴3(OB﹣OE)=2(OB+OE),
∴OB=5OE,
∴,
∴的值是.
6.【解答】(1)证明:∵∠BAD=∠C,∠ABD=∠CBA,
∴△ABD∽△CBA,
∴,
∴AB2=BD BC;
(2)解:过点C作CF⊥AB于点F,过点D作DG⊥AB于点G,
则∠AFC=∠AGD=90°,
∴CF∥DG,∠BAC=60°,
∴,,
∵D为BC的中点,
∴,
∵CF∥DG,
∴△BDG∽△BCF,
∴,
∴,
∴,
∴,
∴,
∵AC=CD,
∴∠CAD=∠CDA,
∵∠AED=∠CAD,
∴∠AED=∠CDA,
∴∠AED+∠BED=∠ADC+∠ADB=180°,
∴∠BED=∠ADB,
∵∠DBE=∠ABD,
∴△BED∽△BDA,
∴,即,
解得:;
(3)解:连接BD,
∵四边形ABCD为菱形,
∴,AD=AB=BC=5,AD∥BC,
∵∠ABC=2∠EBF,
∴∠ABD=∠CBD=∠EBF,
∴∠EBF﹣∠DBF=∠CBD﹣∠DBF,即∠DBE=∠CBF,
∵AD∥BC,
∴∠CBF=∠G,
∴∠DBE=∠G,
∵∠DEB=∠BEG,
∴△BED∽△GEB,
∴,
∵DG=6,
∴EG=DE+6,
∴,
解得:DE=2,负值舍去,
∴EG=2+6=8,
∴AE=AD﹣DE=3,
∵AE2+BE2=32+42=52=AB2,
∴△ABE为直角三角形,∠AEB=90°,
∴∠BEG=180°﹣90°=90°,
∴在Rt△BEG中根据勾股定理得:,
∴,
∵AD∥BC,
∴△DFG∽△CFB,
∴,
即,
解得:.
7.【解答】(1)证明:∵正方形ABCD,
∴∠B=90°,
∵FG⊥BC,
∴∠G=90°,
由∠B=∠G,∠1=∠2,AE=EF,
得△ABE≌△EGF(AAS);
(2)①证明:连BP.
由(1)得△ABE≌△EGF,
∴∠AEB=∠EFG,
∴∠AEB+∠GEF=∠AEB+∠BAE=90°,
即∠AEF=90°,
∴△AEF是等腰直角三角形,
∵EM⊥AF,
∴∠APE=90°,∠AEP=∠FEP=45°,
∵∠ABE=90°,
∴A、B、E、P四点共圆,
∴∠ABP=∠AEP=45°,
∵∠ABE=90°,∠ABP=∠CBP=45°,
∴点
P
在∠ABC的平分线上;
②m+1.
理由如下:
由①得点
P
在∠ABC的平分线即正方形的对角线上,如图:
∵正方形ABCD,
∴AB∥HD,
∴△ABP∽△HDP,
∴,
∵m,
∴HC=mHD,
∴DC=DH+HC=(m+1)HD,
∴m+1;
③由①得点
P
在∠ABC的平分线即正方形的对角线上,
∴∠PDH=45°,
同理M、D、H、P四点共圆,
∴∠PMH=∠PDH=45°,
∵∠AEP=∠NEM=45°,
∴∠EMH=∠NEM=45°,
∴MH∥EN,
∵MN∥HE,
∴四边形MNEH是平行四边形,
∵△AEF是等腰直角三角形,
∴△PHQ和△PHM都是等腰直角三角形,
设PM=PH=a,则MQ=2a,ME=2MQ=4a,
∵PM=PH,PA=PE,
∴AH=ME=4a,
∴AP=3a,
则AE=3a,
∴BE,
∵∠APM=∠ADH,
∴△APM∽△ADH,
∴,
∴DH,
∴AH2,
∵AH=4a,
∴4a=2,
∴a,
∴BE3.
8.【解答】(1)证明:如图2,∵∠A=∠A,∠ACD=∠B,
∴△ACD∽△ABC,
∴,
∴AC2=AD AB.
(2)解:如图3,设AD=m,
∵点D为AB中点,
∴AD=BD=m,AB=2m,
由(1)得△ACD∽△ABC,
∴,
∴AC2=AD AB=m×2m=2m2,
∴ACm或ACm(不符合题意,舍去),
∴,
∵BC=4,
∴CDBC4=2,
∴CD的长是2.
(3)解法一:如图4,作BF⊥DC交DC的延长线于点F,则∠F=90°,
∵点E为CD中点,
∴CE=DE,
设CE=DE=n,
∵∠CDB=∠CBD=30°,
∴CB=CD=2n,∠BCF=∠CDB+∠CBD=60°,
∴∠FBC=90°﹣∠BCF=30°,
∴CFCB=n,
∴EF=CE+CF=2n,BFn,
∴BD=2BF=2n,BEn,
作CH∥EB交AB的延长线于点H,则△HDC∽△BDE,
∴2,
∴HC=2BE=2n,HD=2BD=4n,
∵∠ACD=∠EBD,∠H=∠EBD,
∴∠ACD=∠H,
∵∠A=∠A,
∴△ACD∽△AHC,
∴,
∵AC=2,
∴ADAC22,AHAC214,
∴HD=AH﹣AD=14﹣2=12,
∴4n=12,
解得n,
∴BE,
∴BE的长是.
解法二:如图5,取BD中点M,连接CM、EM,
∵点E为CD中点,
∴DM是△BCD的中位线,
∴EM∥CB,
∵∠CDB=∠CBD=30°,
∴CD=CB,∠EMD=∠CBD=30°,
∴CM⊥BD,∠ADC=∠BME=180°﹣30°=150°,
∵∠ACD=∠EBD,即∠ACD=∠EBM,
∴△ACD∽△EBM,
∵∠CMB=90°,∠CBM=30°,AC=2,
∴CD=CB=2CM,
设CM=x,则CD=CB=2x,
∴BMx,
∴,
∴BEAC2,
∴BE的长是.
9.【解答】(1)证明:∵四边形ABCD是正方形,
∴∠PAE=∠QCE=45°,
∵CE=2AE,AP=t,CQ=2t,
∴,
∴△AEP∽△CEQ;
(2)解:方法一:过点E作EM⊥AB于点M,过点E作 EN⊥BC于点N.
由题意知AE,AM=ME=2,EN=CN=4,AP=t,
CQ=2t,BQ=6﹣2t,MP=|t﹣2|,BP=6﹣t,QN=|2t﹣4|,
∴EP2=EM2+MP2,即EP2=22+(2﹣t)2=t2﹣4t+8,
PQ2=BP2+BQ2,即PQ2=(6﹣t)2+(6﹣2t)2=5t2﹣36t+72,
EQ2=EN2+NQ2,即EQ2=42+(2t﹣4)2=4t2﹣16t+32,
①当∠EPQ=90°时,则EQ2=EP2+PQ2,
即4t2﹣16t+32=t2﹣4t+8+5t2﹣36t+72,
整理得t2﹣12t+24=0.
解得t1=6,t2=6(不合题意,舍去),
②当∠PEQ=90°时,则PQ2=EP2+EQ2,
即5t2﹣36t+72=t2﹣4t+8+4t2﹣16t+32,
整理得t﹣2=0,
解得t=2;
③当∠PQE=90°时,则EP2=PQ2+EQ2,
即t2﹣4t+8=5t2﹣36t+72+4t2﹣16t+32,
整理得t2﹣6t+12=0,该方程无实数解,
综上所述,当△EPQ是直角三角形时,t的值为秒或2秒;
(3)解:方法一:过点A作AF⊥AC,交CB的延长线于点F,连接FE交AQ于点G.如图2,
∵AF⊥AC,∠ACF=45°,
∴AF=AC,
又∵CE=2AE,
∴,
∴tan∠AFE,
∵tan∠AQE,
∴∠AFE=∠AQE,
∵∠AGF=∠EGQ,
∴△AGF∽△EGQ,
∴,
∵∠AGE=∠FGQ,
∴△AGE∽△FGQ,
∴∠AEG=∠FQG,
∵∠AFE+∠AEF=90°,
∴∠FQG+∠EQG=90°,即∠FQE=90°,
∴AB∥EQ,△EQC是等腰直角三角形,
∴,即,
∴QC=QE=4,
∴S△AEQ=S△AQC﹣S△EQC
QC ABQC EQ
4×64×4
=4(cm2).
方法二:∵AF⊥AC,∠ACF=45°,
∴AF=AC,
又∵CE=2AE,
∴,
∴tan∠AFE,
∵tan∠AQE,
∴∠AFE=∠AQE,
∴A,F,Q,E四点共圆,直径为EF,如图3,
∴∠FQE=90°,
∴AB∥EQ,△EQC是等腰直角三角形,
∴,即,
∴QC=QE=4,
∴S△AEQ=S△AQC﹣S△EQC
QC ABQC EQ
4×64×4
=4(cm2).
10.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠C=∠ADE=90°,
∴∠CDF+∠DFC=90°,
∵AE⊥DF,
∴∠DGE=90°,
∴∠CDF+∠AED=90°,
∴∠AED=∠DFC,
∴△ADE∽△DCF;
(2)证明:∵四边形ABCD是正方形,
∴AD=DC,AD∥BC,∠ADE=∠DCF=90°,
∵AE=DF,
∴Rt△ADE≌Rt△DCF(HL),
∴DE=CF,
∵CH=DE,
∴CF=CH,
∵点H在BC的延长线上,
∴∠DCH=∠DCF=90°,
又∵DC=DC,
∴△DCF≌△DCH(SAS),
∴∠DFC=∠H,
∵AD∥BC,
∴∠ADF=∠DFC,
∴∠ADF=∠H;
(3)解:如图3,延长BC至点G,使CG=DE=8,连接DG,
∵四边形ABCD是菱形,
∴AD=DC,AD∥BC,
∴∠ADE=∠DCG,
∴△ADE≌△DCG(SAS),
∴∠DGC=∠AED=60°,AE=DG,
∵AE=DF,
∴DG=DF,
∴△DFG是等边三角形,
∴FG=DF=11,
∵CF+CG=FG,
∴CF=FG﹣CG=11﹣8=3,
即CF的长为3.
11.【解答】(1)①证明:如图1中,∵四边形ABCD是正方形,
∴∠A=∠D=90°,
∵∠CEF=90°,
∴∠AEF+∠CED=90°,∠ECD+∠CED=90°,
∴∠AEF=∠ECD,
∴△AEF∽△DCE;
②解:如图2中,延长DA交CF的延长线于点G,过点G作GH⊥CE交CE的延长线于点H.
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴,
∵CD=2,AE=ED=1,
∴GH=2HE,
设EH=m,GH=2m.
∵CE,
∴CH=m,
∵tan∠ECF,
∴,
∴m,
∴EH,GH,
∴EG,
∴AG=EG﹣AE1,DG=EG+DE1,
∵AF∥CD,
∴,
∴,
∴AF;
(3)证明:如图3中,过点G作GH⊥CE交CE的延长线于点H.
设AD=CD=a,GE=DE=t,EH=x,GH=y,CE=n,
∵∠H=∠D=90°,∠GEH=∠CED,
∴△GEH∽△CED,
∴
∴,
∴x,y,
在Rt△CGH中,sin∠ECF,
∴CG=3GH,CH=2GH,
∴,
∴2y=x+n,
∴2n,
∴2at=t2+n2,
在Rt△CDE中,n2=t2+a2,
∴2at=2t2+a2,
∴at,
∵AF∥CD,
∴,
∴,
∴AFaa﹣t,
∵AE=a﹣t,
∴AE=AF.
解法二:设AE=x,则DE=EG=1﹣x,DG=2﹣2x,
∴S△CDE=S△CEG,
∴(1﹣x)×1 ,
解得x=1(负根已经舍去),
∴AE=1,
由AF:CD=AG:DG,可得AF:1=(1):,
∴AF=1.
∴AE=AF.
12.【解答】(1)证明:∵∠A+∠AGA'=90°,∠A'+∠AGA'=90°,
∴∠A=∠A',
∵AD=A'D,∠ADE=∠A'DG=90°,
∴△ADE≌△A′DG(ASA);
(2)证明:∵∠AFG=∠ACB=90°,∠FAG=∠CAB,
∴△AFG∽△ACB,
∴,
∴,
∵∠FAC=∠GAB,
∴△FAC∽△GAB,
∴,
∴AF GB=AG FC;
(3)解:∵tanA,AC=8,
∴BC=4,
∴S△ACB=16,
设DE=DG=x,则AD=A'D=2x,AE=A'Gx,
∴A'E=A'D﹣DE=2x﹣x=x,
∴S△ADE=S△A′DG=x2,
∵△A'FE∽△A'DG,
∴,
∴S△A'FE:S△A'DG=1:5,
∴S四边形DGFES△A'DGx2,
∵S△ACB=S△ADE+S四边形DCBE,A′G平分四边形DCBE的面积,
∴S△ACB=S△ADE+2S四边形DGFE,
∴16=x2x2,
x2
∴x1,x2(舍),
∴AD.
13.【解答】解:(1)如图1,连接OD,
∵CD切半圆O于点D,
∴OD⊥CE,
∵OA,AC=1,
∴OC,BC=4,
∴CD2,
∵BE⊥CE,
∴OD∥BE,
∴,
∴,
∴CE,
如图2,∵∠AFB=∠E=90°,
∴AF∥CE,
∴MN∥CB,
∴四边形APMC是平行四边形,
∴CM=PAx,
∵NM∥BC,
∴△BCE∽△NME,
∴,
∴,
∴yx+4;
(2)∵PN=y﹣1x+4﹣1x+3,PH<PN,△BCE的三边之比为3:4:5,
∴可分为三种情况,
当PH:PN=3:5时,xx+3,解得:x,
∴ax,
当PH:PN=4:5时,xx+3,解得:x,
∴ax,
当PH:PN=3:4时,xx+3,解得:x,
∴ax,
综上所述:a的值为或或;
(3)如图3,连接AQ,BQ,过点Q作QG⊥AB于点G,
则∠AQB=∠AGQ=90°,PH=QG=x,
∴∠QAB=∠BQG,
∵NQx﹣3,PN=y﹣1x+3,
∴HG=PQ=NQ+PNx,
∵AHx,
∴AG=AH+HG=3x,
∴tan∠BQG=tan∠QAB,
∴BGQGx,
∴AB=AG+BGx=3,
∴x,
∴yx+4,
∴MN的长为.
14.【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD=CB=CD,∠ABC=∠ADC=90°,
∴∠BAC=∠BCA=∠DAC=∠DCA=45°,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS).
(2)解:△FBG是等腰三角形,理由如下:
∵△ABE≌△ADE,
∴∠ABE=∠ADE,
∴∠ABC﹣∠ABE=∠ADC﹣∠ADE,
∴∠EBC=∠EDC,
∵AB∥CD,
∴∠FGB=∠EDC,
∴∠FGB=∠EBC,
∵BF⊥BE,
∴∠FBE=90°,
∴∠FBG=∠EBC=90°﹣∠ABE,
∴∠FGB=∠FBG,
∴BF=GF,
∴△FBG是等腰三角形.
(3)解:∵BE=BF=2,∠FBE=90°,
∴∠F=∠BEF=45°,
∴∠BAC=∠F,
∴∠AEG=∠AGF﹣∠BAC=∠AGF﹣∠F=∠FBG,
∵∠AGE=∠FGB,且∠FGB=∠FBG,
∴∠AGE=∠AEG,
∴AE=AG,
∵EF2,BF=GF=2,
∴GE=EF﹣GF=22,
∵△ABE≌△ADE,
∴BE=DE=2,
∵AG∥CD,
∴△AGE∽△CDE,
∴1,
∴1,
∴的值为1.
15.【解答】(1)证明:∵EF⊥AB,AM是BC边上的高,
∴∠AMB=∠EFB=90°,
又∵∠B=∠B,
∴△ABM∽△EBF;
(2)解:过点E作EN⊥AD于点N,如图:
在平行四边形ABCD中,AD∥BC,
又∵AM是BC边上的高,
∴AM⊥AD,
∴∠AME=∠MAN=∠ANE=90°,
∴四边形AMEN为矩形,
∴NE=AM=4,AN=ME,
在Rt△ABM中,,
又∵E为BC的中点,
∴,
∴ME=AN=2,
∴DN=8,
在Rt△DNE中,;
(3)解:延长FE交DC的延长线于点G,如图:
∵sinB,
∴,
∴EFx,
∵AB∥CD,
∴∠B=∠ECG,∠EGC=∠BFE=90°,
又∵∠AMB=∠EGC=90°,
∴△ABM∽△ECG,
∴,
∴,
∴GC(10﹣x),
∴DG=DC+GC=5(10﹣x),
∴yEF DGx [5(10﹣x)]x2x(x)2,
∴当x时,y有最大值为,
答:yx2x,当x时,y有最大值为.
16.【解答】(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,
∴∠CED+∠DCE=90°,
∵EF⊥CE,
∴∠CED+∠AEF=90°,
∴∠DCE=∠AEF,
∴△AEF∽△DCE;
(2)解:①连接AM,如图2,
∵BG⊥CF,
∴△BGC是直角三角形,
∵点M是BC的中点,
∴MB=CM=GM,
∴点G在以点M为圆心,3为半径的圆上,
当A,G,M三点不共线时,由三角形两边之和大于第三边得:AG+GM>AM,
当A,G,M三点共线时,AG+GM=AM,
此时,AG+GM取得最小值,
在Rt△ABM中,AM5,
∴AG+GM的最小值为5.
②方法一:
如图3,过点M作MN∥AB交FC于点N,
∴△CMN∽△CBF,
∴,
设AF=x,则BF=4﹣x,
∴MNBF(4﹣x),
∵MN∥AB,
∴△AFG∽△MNG,
∴,
由(2)可知AG+GM的最小值为5,
即AM=5,
又∵GM=3,
∴AG=2,
∴,
解得x=1,
即AF=1,
由(1)得,
设DE=y,则AE=6﹣y,
∴,
解得:y=3或y=3,
∵06,0<36,
∴DE=3或DE=3.
方法二:
如图4,过点G作GH∥AB交BC于点H,
∴△MHG∽△MBA,
∴,
由(2)可知AG+MG的最小值为5,
即AM=5,
又∵GM=3,
∴,
∴GH,MH,
由GH∥AB得△CHG∽△CBF,
∴,
即,
解得FB=3,
∴AF=AB﹣FB=1.
由(1)得,
设DE=y,则AE=6﹣y,
∴,
解得:y=3或y=3,
∵06,0<36,
∴DE=3或DE=3.
17.【解答】(1)①证明:如图1,
∵AD=CD,
∴∠DAC=∠DCA.
∵AD∥BC,
∴∠DAC=∠ACB.
∵BO是Rt△ABC斜边AC上的中线,
∴OB=OC,
∴∠OBC=∠OCB,
∴∠DAC=∠DCA=∠ACB=∠OBC,
∴△DAC∽△OBC;
②解:如图2,若BE⊥CD,
在Rt△BCE中,∠OCE=∠OCB=∠EBC,
∴∠OCE=∠OCB=∠EBC=30°.
过点D作DH⊥BC于点H,
设AD=CD=2m,则BH=AD=2m,
在Rt△DCH中,DC=2m,
∴CH=m,
∴BC=BH+CH=3m,
∴;
(2)①如图3,当点E在AD上时,
∵AD∥BC,
∴∠EAO=∠BCO,∠AEO=∠CBO,
∵O是AC的中点,
∴OA=OC,
∴△AOE≌△COB(AAS),
∴OB=OE,
∴四边形ABCE是平行四边形,
又∵∠ABC=90°,
∴四边形ABCE是矩形.
设AD=CD=x,
∵DE=2,
∴AE=x﹣2,
∵OE=3,
∴AC=6,
在Rt△ACE和Rt△DCE中,CE2=AC2﹣AE2,CE2=CD2﹣DE2,
∴62﹣(x﹣2)2=x2﹣22,
解得x=1,或x=1(舍去).
∴CD=1.
②如图4,当点E在CD上时,设AD=CD=x,则CE=x﹣2,
设OB=OC=m,
∵OE=3,
∴EB=m+3,
∵△DAC∽△OBC,
∴,
∴,
∴.
又∵∠EBC=∠OCE,∠BEC=∠OEC,
∴△EOC∽△ECB,
∴,
∴,
∴,
∴m,
将m代入,
整理得,x2﹣6x﹣10=0,
解得x=3,或x=3(舍去).
∴CD=3.
综合以上可得CD的长为1或3.
21世纪教育网(www.21cnjy.com)
同课章节目录
