2025年九年级数学中考三轮冲刺训练圆中相似三角形专题训练(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练圆中相似三角形专题训练(含答案) | 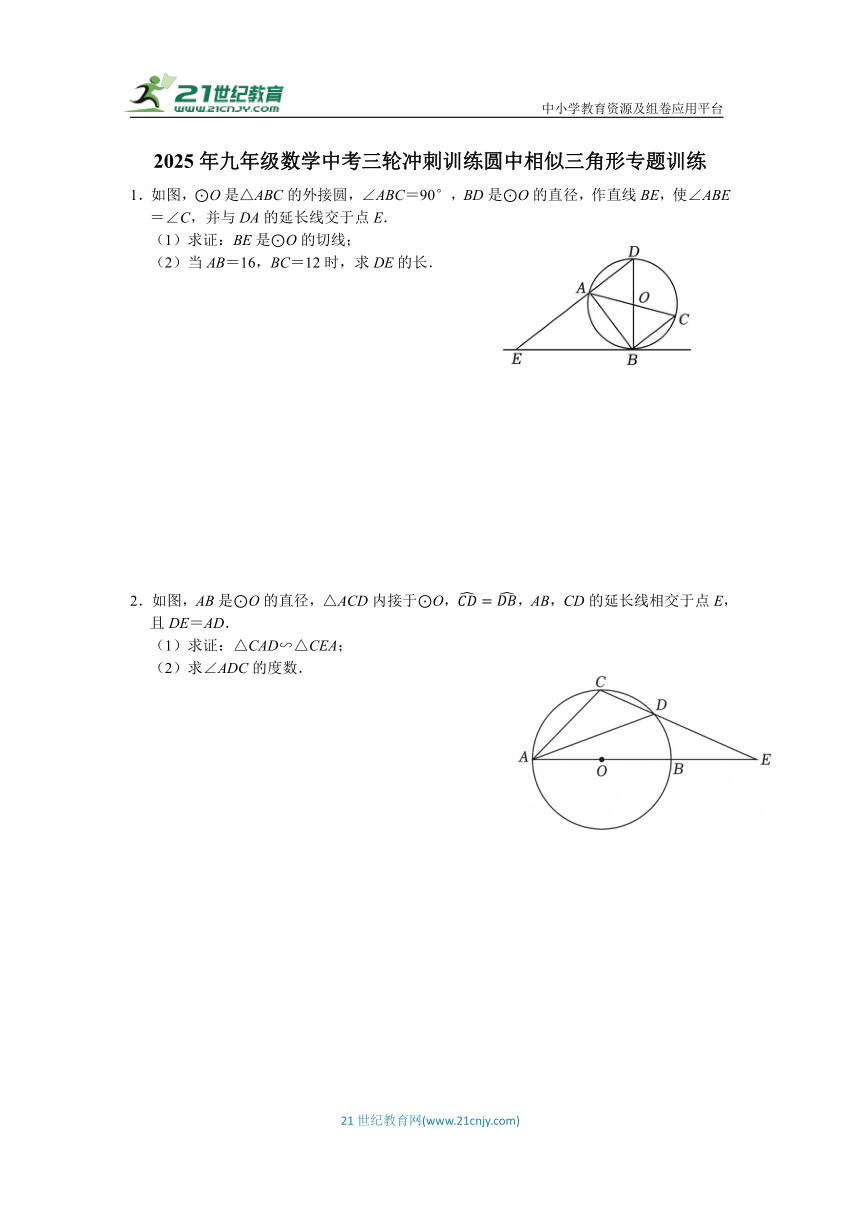 | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 19:29:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练圆中相似三角形专题训练
1.如图,⊙O是△ABC的外接圆,∠ABC=90°,BD是⊙O的直径,作直线BE,使∠ABE=∠C,并与DA的延长线交于点E.
(1)求证:BE是⊙O的切线;
(2)当AB=16,BC=12时,求DE的长.
2.如图,AB是⊙O的直径,△ACD内接于⊙O,,AB,CD的延长线相交于点E,且DE=AD.
(1)求证:△CAD∽△CEA;
(2)求∠ADC的度数.
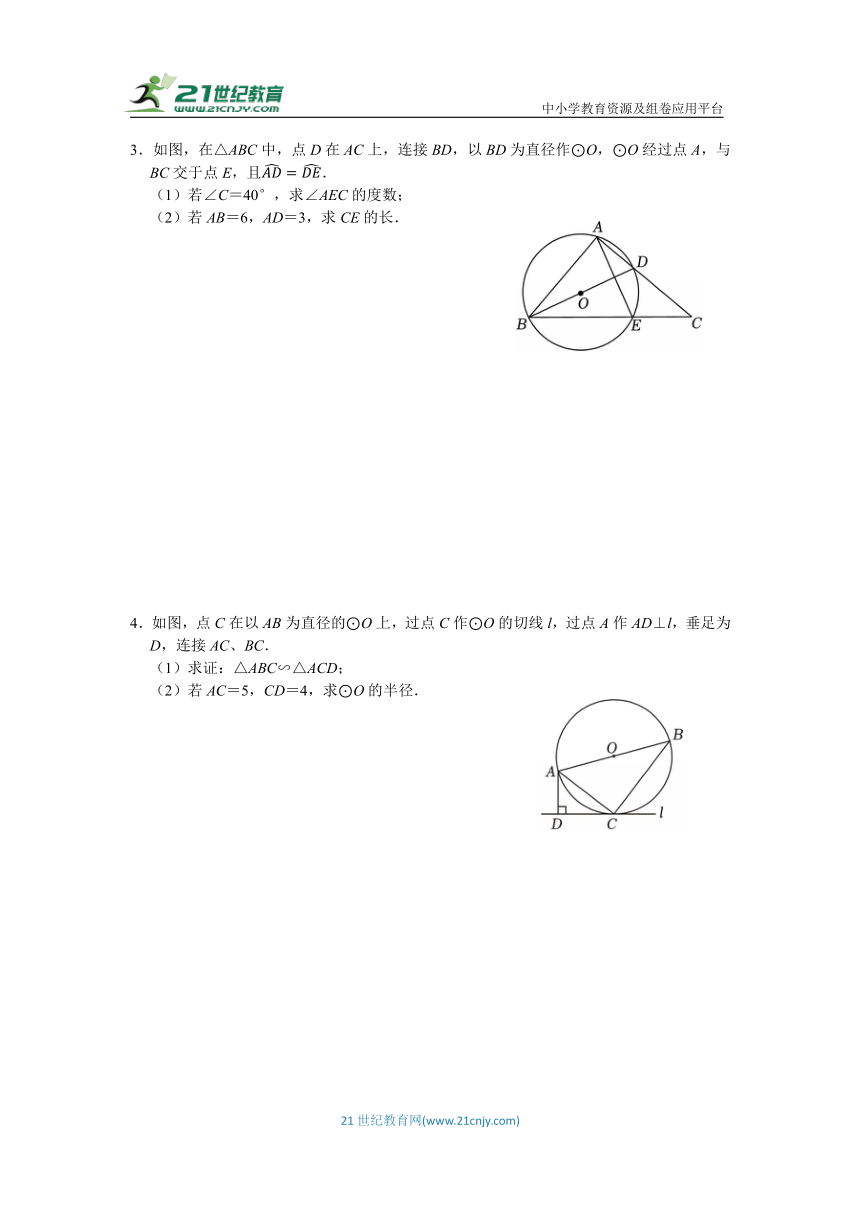
3.如图,在△ABC中,点D在AC上,连接BD,以BD为直径作⊙O,⊙O经过点A,与BC交于点E,且.
(1)若∠C=40°,求∠AEC的度数;
(2)若AB=6,AD=3,求CE的长.
4.如图,点C在以AB为直径的⊙O上,过点C作⊙O的切线l,过点A作AD⊥l,垂足为D,连接AC、BC.
(1)求证:△ABC∽△ACD;
(2)若AC=5,CD=4,求⊙O的半径.
5.如图,△ABC内接于⊙O,点D为的中点,连接AD、BD,BE平分∠ABC交AD于点E,过点D作DF∥BC交AC的延长线于点F.
(1)求证:DF是⊙O的切线.
(2)求证:BD=ED.
(3)若DE=5,CF=4,求AB的长.
6.如图,在⊙O中,AB是⊙O的直径,弦CD交AB于点E,.
(1)求证:△ACD∽△ECB;
(2)若AC=3,BC=1,求CE的长.
7.如图,在Rt△ABC中,∠C=90°,D为斜边AB上一点,以BD为直径作⊙O,交AC于E,F两点,连接BE,BF,DF.
(1)求证:BC DF=BF CE;
(2)若∠A=∠CBF,tan∠BFC,AF=4,求CF的长和⊙O的直径.
8.如图,BC是⊙O的直径,A是⊙O上异于B、C的点.⊙O外的点E在射线CB上,直线EA与CD垂直,垂足为D,且DA AC=DC AB.设△ABE的面积为S1,△ACD的面积为S2.
(1)判断直线EA与⊙O的位置关系,并证明你的结论;
(2)若BC=BE,S2=mS1,求常数m的值.
9.如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,AC,BC=2,点F在AB上,连接CF并延长,交⊙O于点D,连接BD,作BE⊥CD,垂足为E.
(1)求证:△DBE∽△ABC;
(2)若AF=2,求ED的长.
10.如图,点D,E在以AC为直径的⊙O上,∠ADC的平分线交⊙O于点B,连接BA,EC,EA,过点E作EH⊥AC,垂足为H,交AD于点F.
(1)求证:AE2=AF AD;
(2)若sin∠ABD,AB=5,求AD的长.
11.如图,AB是⊙O的直径,AM是⊙O的切线,AC、CD是⊙O的弦,且CD⊥AB,垂足为E,连接BD并延长,交AM于点P.
(1)求证:∠CAB=∠APB;
(2)若⊙O的半径r=5,AC=8,求线段PD的长.
12.如图,在Rt△ABC中,∠ACB=90°, ODEF的顶点O,D在斜边AB上,顶点E,F分别在边BC,AC上,以点O为圆心,OA长为半径的⊙O恰好经过点D和点E.
(1)求证:BC与⊙O相切;
(2)若sin∠BAC,CE=6,求OF的长.
13.如图,四边形ABCD内接于圆O,AB是直径,点C是的中点,延长AD交BC的延长线于点E.
(1)求证:CE=CD;
(2)若AB=3,BC,求AD的长.
14.在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,点E是边BC的中点,连结DE.
(1)求证:DE是⊙O的切线;
(2)若AD=4,BD=9,求⊙O的半径.
15.如图,在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长交BC的延长线于点F.
(1)求证:BF=BD;
(2)若CF=1,tan∠EDB=2,求⊙O的直径.
参考答案
1.【解答】(1)证明:∵BD是⊙O的直径,
∴∠BAD=90°,
∴∠D+∠ABD=90°,
∵,
∴∠D=∠C,
∴∠C+∠ABD=90°,
∵∠ABE=∠C,
∴∠ABE+∠ABD=90°,
即∠EBD=90°,
∵BD是⊙O的直径,
∴BE是⊙O的切线;
(2)解:在△ABC中,∠ABC=90°,AB=16,BC=12,
由勾股定理得,,
∵∠ABC=90°,
∴AC为⊙O的直径,
∵BD是⊙O的直径,
∴BD=AC=20,∠BAD=90°,
由勾股定理得,AD,
由(1)知∠EBD=90°,
∴∠EBD=∠BAD=90°,
又∵∠D为公共角,
∴△BDA∽△EBD,
∴,
∴,
∴DE.
2.【解答】(1)证明:∵,
∴∠CAD=∠DAB,
∵DE=AD,
∴∠DAB=∠E,
∴∠CAD=∠E,
又∵∠C=∠C
∴△CAD∽△CEA,
(2)连接BD,如图:
∵AB为直径,
∴∠ADB=90°,
设∠CAD=∠DAB=α,
∴∠CAE=2α,
由(1)知:△CAD∽△CEA,
∴∠ADC=∠CAE=2α,
∵四边形ABDC是圆的内接四边形,
∴∠CAB+∠CDB=180°,
即2α+2α+90°=180°,
解得:α=22.5°
∠ADC=∠CAE=2×22.5°=45°
3.【解答】解:(1)∵BD为直径,
∴∠BAD=90°,
∵∠C=40°,
∴∠ABC=90°﹣40°=50°,
∵,
∴∠ABD=∠DBC∠ABC=25°,
∴∠ADB=90°﹣25°=65°,
∴∠AEB=∠ADB=65°,
∴∠AEC=115°.
(2)连接DE,
∵
∴DE=AD=3,
∵BD为直径,
∴,
∴BE=AB=6,
∵BD为直径,
∴∠BED=90°,
∴∠CED=180°﹣90°=90°,
∴∠CED=∠CAB,
∵∠C=∠C,
∴△CED∽△CAB,
∴,
设CE=x,CD=y,则,
∴,
∴CE=4.
4.【解答】(1)证明:连接OC,
∵l是⊙O的切线,
∴OC⊥l,
∵AD⊥l,
∴OC∥AD,
∴∠CAD=∠ACO=∠CAB,
∵∠D=∠ACB=90°,
∴△ABC∽△ACD;
(2)解:∵AC=5,CD=4,∠ADC=90°,
∴AD3,
∵△ABC∽△ACD,
∴,
∴,
∴AB,
∴半径为.
5.【解答】(1)证明:如图,连接OD,
∵点D为的中点,O为圆心,
∴OD⊥BC,
∵DF∥BC,
∴OD⊥DF,
∵OD为⊙O的半径,
∴DF是⊙O的切线;
(2)证明:∵点D为的中点,
∴,
∴∠DBC=∠BAD,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠DEB是△ABE的外角,
∴∠DEB=∠BAE+∠ABE,
∵∠DBE=∠CBE+DBC,
∴∠DEB=∠DBE,
∴BD=ED;
(3)解:如图,连接CD,
∵四边形ABDC是圆内接四边形,
∴∠ABD+∠ACD=180°,
∵∠DCF+∠ACD=180°,
∴∠ABD=∠DCF,
∵DF∥BC,
∴∠ACB=∠F,
∵∠ACB=∠ADB,
∴∠ADB=∠F,
∴△ABD∽△DCF,
∴,
∵点D为的中点,
∴,
∴BD=CD,
由(2)知BD=ED,
∴CD=BD=DE=5,
∵CF=4,
∴,
∴AB.
6.【解答】(1)证明:∵,
∴∠ACD=∠BCE,
∵∠ADC=∠EBC,
∴△ACD∽△ECB;
(2)解:过B点作BH⊥CD于H点,如图,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ACB中,AB,
∵∠ACD=∠BCD=45°,
∴∠ABD=∠BAD=45°,
∴△ABD为等腰直角三角形,
∴BDAB,
在Rt△BCH中,
∵∠BCH=45°,
∴CH=BHBC,
在Rt△BDH中,DH,
∴CD=CH+DH2,
∵△ACD∽△ECB,
∴CA:CE=CD:CB,即3:CE=2:1,
解得CE,
即CE的长为.
7.【解答】(1)证明:∵BD是⊙O的直径,
∴∠BFD=90°,
∵∠C=90°,
∴∠BFD=∠C,
∵,
∴∠BEC=∠BDF,
∴△BCE∽△BDF,
∴,
∴BC DF=BF CE;
(2)解:连接DE,过E作EH⊥BD于H,如图:
∵∠C=90°,tan∠BFC,
∴,
∴BCCF,
∵∠A=∠CBF,
∴90°﹣∠A=90°﹣∠CBF,即∠ABC=∠BFC,
∴tan∠ABC=tan∠BFC,
∴,
∴ACBC(CF)=5CF,
∵AC﹣CF=AF=4,
∴5CF﹣CF=4,
∴CF,
∴BCCF=5,AC=5CF=5,
∴AB5,
由(1)知△BCE∽△BDF,
∴∠CBE=∠DBF,
∴∠CBE﹣∠FBE=∠DBF﹣∠FBE,即∠CBF=∠EBA,
∵∠A=∠CBF,
∴∠A=∠EBA,
∴AE=BE,
∴BH=AHAB,
∵∠BEH=90°﹣∠EBA=90°﹣∠CBF=∠BFC,
∴tan∠BEH=tan∠BFC,
∴,即,
∴EH,
∵BD是⊙O的直径,
∴∠BED=90°,
∴∠EDH=90°﹣∠DEH=∠BEH,
∴tan∠EDH=tan∠BEH,
∴,即,
∴DH,
∴BD=DH+BH3,
∴⊙O的直径为3.
答:CF的长为,⊙O的直径为3.
8.【解答】解:(1)AE与⊙O相切,理由如下:
如图,连接OA,
∵DA AC=DC AB,
∴,
∵BC是⊙O的直径,
∴∠BAC=90°=∠ADC,
∴△ABC∽△DAC,
∴∠ACB=∠ACD,
∵OA=OC,
∴∠OAC=∠ACB=∠ACD,
∴OA∥CD,
∴∠OAE=∠CDE=90°,
∴OA⊥DE,
又∵OA为半径,
∴AE与⊙O相切;
(2)如图,∵OA∥CD,
∴△AOE∽△DCE,
∴,
设BO=OC=OA=a,则BC=2a,
∵BC=BE=2a,
∴S△ABE=S△ABC,EO=3a,EC=4a,
∴,
∴CDa,
∵△ABC∽△DAC,
∴,
∴AC2=BC CDa2,
∵△ABC∽△DAC,
∴()2,
∴S2S1,
∴m.
9.【解答】(1)证明:∵AB为直径,
∴∠ACB=90°,
∵BE⊥CD,
∴∠BED=90°,
∵ 所对的圆周角为∠BDE和∠BAC,
∴∠BDE=∠BAC,
∴△DBE∽△ABC;
(2)解:如图,过点C作CG⊥AB,垂足为G,
∵∠ACB=90°,AC,BC=2,
∴AB5,
∵CG⊥AB,
∴AG=ACcosA1,
∵AF=2,
∴FG=AG=1,
∴CG是AF的垂直平分线,
∴AC=FC,
∴∠CAF=∠CFA=∠BFD=∠BDF,
∴BD=BF=AB﹣AF=5﹣2=3,
∵△DBE∽△ABC,
∴,
∴,
∴ED.
10.【解答】(1)证明:∵EH⊥AC于点H,AC是⊙O的直径,
∴∠AHE=∠AEC=90°,
∵∠HAE=∠EAC,
∴△HAE∽△EAC,
∴,
∴AE2=AH AC,
∵∠HAF=∠DAC,∠AHF=∠ADC=90°,
∴△AHF∽△ADC,
∴,
∴AH AC=AF AD,
∴AE2=AF AD.
(2)解:连接BC,
∵∠ADC的平分线交⊙O于点B,
∴∠ADB=∠CDB,
∴,
∴AB=BC=5,
∵∠ABC=90°,
∴AC5,
∵∠ACD=∠ABD,
∴sin∠ACD=sin∠ABD,
∴ADAC52,
∴AD的长是2.
11.【解答】(1)证明:∵AM是⊙O的切线,
∴∠BAM=90°,
∵∠CEA=90°,
∴AM∥CD,
∴∠CDB=∠APB,
∵∠CAB=∠CDB,
∴∠CAB=∠APB.
(2)解:如图,连接AD,
∵AB是直径,
∴∠CDB+∠ADC=90°,
∵∠CAB+∠C=90°,∠CDB=∠CAB,
∴∠ADC=∠C,
∴AD=AC=8,
∵AB=10,
∴BD=6,
∵∠BAD+∠DAP=90°,∠PAD+∠APD=90°,
∴∠APB=∠DAB,
∵∠BDA=∠BAP
∴△ADB∽△PAB,
∴,
∴PB,
∴DP6.
故答案为:.
12.【解答】(1)证明:连接OE,
∵四边形ODEF是平行四边形,
∴EF∥OD,EF=OD,
∵OA=OD,
∴EF∥OA,EF=OA,
∴四边形AOEF是平行四边形,
∴OE∥AC,
∴∠OEB=∠ACB,
∵∠ACB=90°,
∴∠OEB=90°,
∴OE⊥BC,
∵OE是⊙O的半径,
∴BC与⊙O相切;
(2)解:过点F作FH⊥OA于点H,
∵四边形AOEF是平行四边形,
∴EF∥OA,
∴∠CFE=∠CAB,
∴sin∠CFE=sin∠CAB,
在Rt△CEF中,∠ACB=90°,
∵CE=6,sin∠CFE,
∴EF,
∵四边形AOEF是平行四边形,且OA=OE,
∴ AOEF是菱形,
∴AF=AO=EF=10,
在Rt△AFH中,∠AHF=90°,
∵AF=10,sin∠CAB,
∴FH=AF,
∵AH2=AF2﹣FH2,
∴AH,
∴OH=AO﹣AH=10﹣8=2,
在Rt△OFH中,∠FHO=90°,
∵OF2=OH2+FH2,
∴OF,
∴OF=2.
13.【解答】(1)证明:连接AC,
∵AB为直径,
∴∠ACB=∠ACE=90°,
又∵点C是的中点
∴∠CAE=∠CAB,CD=CB,
又∵AC=AC
∴△ACE≌△ACB(ASA),
∴CE=CB,
∴CE=CD;
(2)解:∵△ACE≌△ACB,AB=3,
∴AE=AB=3,
又∵四边形ABCD内接于圆O,
∴∠ADC+∠ABC=180°,
又∵∠ADC+∠CDE=180°,
∴∠CDE=∠ABE,
又∵∠E=∠E,
∴△EDC∽△EBA,
∴,
即:,
解得:DE=2,
∴AD=AE﹣DE=1.
14.【解答】(1)证明:连接OD,CD,
∵∠ACB=90°,
∴∠ACD+∠DCB=90°,
∵OC=OD,
∴∠OCD=∠ODC,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠CDB=180°﹣∠ADC=90°,
∵点E是边BC的中点,
∴DE=CEBC,
∴∠DCE=∠CDE,
∴∠ODC+∠CDE=90°,
∴∠ODE=90°,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)解:∵AD=4,BD=9,
∴AB=AD+BD=4+9=13,
∵∠ACB=∠ADC=90°,∠A=∠A,
∴△ACB∽△ADC,
∴,
∴AC2=AD AB=4×13=52,
∴AC=2,
∴⊙O的半径为.
15.【解答】(1)证明:连接OE,如图,
∵AC是⊙O的切线,
∴OE⊥AC.
∵AC⊥BC,
∴OE∥BC,
∴∠OED=∠F.
∵OD=OE,
∴∠ODE=∠OED,
∴∠BDE=∠F,
∴BD=BF;
(2)解:连接BE,如图,
∵∠BDE=∠F,
∴tan∠BDE=tan∠F=2,
∵CF=1,tan∠F,
∴CE=2.
∵BD是⊙O直径,
∴∠BED=90°,
∴BE⊥EF.
∵EC⊥BF,
∴△ECF∽△BCE,
∴,
∴EC2=BC CF.
∴BC=4.
∴BF=BC+CF=5.
∴BD=BF=5,
即⊙O的直径为5.
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练圆中相似三角形专题训练
1.如图,⊙O是△ABC的外接圆,∠ABC=90°,BD是⊙O的直径,作直线BE,使∠ABE=∠C,并与DA的延长线交于点E.
(1)求证:BE是⊙O的切线;
(2)当AB=16,BC=12时,求DE的长.
2.如图,AB是⊙O的直径,△ACD内接于⊙O,,AB,CD的延长线相交于点E,且DE=AD.
(1)求证:△CAD∽△CEA;
(2)求∠ADC的度数.
3.如图,在△ABC中,点D在AC上,连接BD,以BD为直径作⊙O,⊙O经过点A,与BC交于点E,且.
(1)若∠C=40°,求∠AEC的度数;
(2)若AB=6,AD=3,求CE的长.
4.如图,点C在以AB为直径的⊙O上,过点C作⊙O的切线l,过点A作AD⊥l,垂足为D,连接AC、BC.
(1)求证:△ABC∽△ACD;
(2)若AC=5,CD=4,求⊙O的半径.
5.如图,△ABC内接于⊙O,点D为的中点,连接AD、BD,BE平分∠ABC交AD于点E,过点D作DF∥BC交AC的延长线于点F.
(1)求证:DF是⊙O的切线.
(2)求证:BD=ED.
(3)若DE=5,CF=4,求AB的长.
6.如图,在⊙O中,AB是⊙O的直径,弦CD交AB于点E,.
(1)求证:△ACD∽△ECB;
(2)若AC=3,BC=1,求CE的长.
7.如图,在Rt△ABC中,∠C=90°,D为斜边AB上一点,以BD为直径作⊙O,交AC于E,F两点,连接BE,BF,DF.
(1)求证:BC DF=BF CE;
(2)若∠A=∠CBF,tan∠BFC,AF=4,求CF的长和⊙O的直径.
8.如图,BC是⊙O的直径,A是⊙O上异于B、C的点.⊙O外的点E在射线CB上,直线EA与CD垂直,垂足为D,且DA AC=DC AB.设△ABE的面积为S1,△ACD的面积为S2.
(1)判断直线EA与⊙O的位置关系,并证明你的结论;
(2)若BC=BE,S2=mS1,求常数m的值.
9.如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,AC,BC=2,点F在AB上,连接CF并延长,交⊙O于点D,连接BD,作BE⊥CD,垂足为E.
(1)求证:△DBE∽△ABC;
(2)若AF=2,求ED的长.
10.如图,点D,E在以AC为直径的⊙O上,∠ADC的平分线交⊙O于点B,连接BA,EC,EA,过点E作EH⊥AC,垂足为H,交AD于点F.
(1)求证:AE2=AF AD;
(2)若sin∠ABD,AB=5,求AD的长.
11.如图,AB是⊙O的直径,AM是⊙O的切线,AC、CD是⊙O的弦,且CD⊥AB,垂足为E,连接BD并延长,交AM于点P.
(1)求证:∠CAB=∠APB;
(2)若⊙O的半径r=5,AC=8,求线段PD的长.
12.如图,在Rt△ABC中,∠ACB=90°, ODEF的顶点O,D在斜边AB上,顶点E,F分别在边BC,AC上,以点O为圆心,OA长为半径的⊙O恰好经过点D和点E.
(1)求证:BC与⊙O相切;
(2)若sin∠BAC,CE=6,求OF的长.
13.如图,四边形ABCD内接于圆O,AB是直径,点C是的中点,延长AD交BC的延长线于点E.
(1)求证:CE=CD;
(2)若AB=3,BC,求AD的长.
14.在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于点D,点E是边BC的中点,连结DE.
(1)求证:DE是⊙O的切线;
(2)若AD=4,BD=9,求⊙O的半径.
15.如图,在△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与AC相切于点E,连接DE并延长交BC的延长线于点F.
(1)求证:BF=BD;
(2)若CF=1,tan∠EDB=2,求⊙O的直径.
参考答案
1.【解答】(1)证明:∵BD是⊙O的直径,
∴∠BAD=90°,
∴∠D+∠ABD=90°,
∵,
∴∠D=∠C,
∴∠C+∠ABD=90°,
∵∠ABE=∠C,
∴∠ABE+∠ABD=90°,
即∠EBD=90°,
∵BD是⊙O的直径,
∴BE是⊙O的切线;
(2)解:在△ABC中,∠ABC=90°,AB=16,BC=12,
由勾股定理得,,
∵∠ABC=90°,
∴AC为⊙O的直径,
∵BD是⊙O的直径,
∴BD=AC=20,∠BAD=90°,
由勾股定理得,AD,
由(1)知∠EBD=90°,
∴∠EBD=∠BAD=90°,
又∵∠D为公共角,
∴△BDA∽△EBD,
∴,
∴,
∴DE.
2.【解答】(1)证明:∵,
∴∠CAD=∠DAB,
∵DE=AD,
∴∠DAB=∠E,
∴∠CAD=∠E,
又∵∠C=∠C
∴△CAD∽△CEA,
(2)连接BD,如图:
∵AB为直径,
∴∠ADB=90°,
设∠CAD=∠DAB=α,
∴∠CAE=2α,
由(1)知:△CAD∽△CEA,
∴∠ADC=∠CAE=2α,
∵四边形ABDC是圆的内接四边形,
∴∠CAB+∠CDB=180°,
即2α+2α+90°=180°,
解得:α=22.5°
∠ADC=∠CAE=2×22.5°=45°
3.【解答】解:(1)∵BD为直径,
∴∠BAD=90°,
∵∠C=40°,
∴∠ABC=90°﹣40°=50°,
∵,
∴∠ABD=∠DBC∠ABC=25°,
∴∠ADB=90°﹣25°=65°,
∴∠AEB=∠ADB=65°,
∴∠AEC=115°.
(2)连接DE,
∵
∴DE=AD=3,
∵BD为直径,
∴,
∴BE=AB=6,
∵BD为直径,
∴∠BED=90°,
∴∠CED=180°﹣90°=90°,
∴∠CED=∠CAB,
∵∠C=∠C,
∴△CED∽△CAB,
∴,
设CE=x,CD=y,则,
∴,
∴CE=4.
4.【解答】(1)证明:连接OC,
∵l是⊙O的切线,
∴OC⊥l,
∵AD⊥l,
∴OC∥AD,
∴∠CAD=∠ACO=∠CAB,
∵∠D=∠ACB=90°,
∴△ABC∽△ACD;
(2)解:∵AC=5,CD=4,∠ADC=90°,
∴AD3,
∵△ABC∽△ACD,
∴,
∴,
∴AB,
∴半径为.
5.【解答】(1)证明:如图,连接OD,
∵点D为的中点,O为圆心,
∴OD⊥BC,
∵DF∥BC,
∴OD⊥DF,
∵OD为⊙O的半径,
∴DF是⊙O的切线;
(2)证明:∵点D为的中点,
∴,
∴∠DBC=∠BAD,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∵∠DEB是△ABE的外角,
∴∠DEB=∠BAE+∠ABE,
∵∠DBE=∠CBE+DBC,
∴∠DEB=∠DBE,
∴BD=ED;
(3)解:如图,连接CD,
∵四边形ABDC是圆内接四边形,
∴∠ABD+∠ACD=180°,
∵∠DCF+∠ACD=180°,
∴∠ABD=∠DCF,
∵DF∥BC,
∴∠ACB=∠F,
∵∠ACB=∠ADB,
∴∠ADB=∠F,
∴△ABD∽△DCF,
∴,
∵点D为的中点,
∴,
∴BD=CD,
由(2)知BD=ED,
∴CD=BD=DE=5,
∵CF=4,
∴,
∴AB.
6.【解答】(1)证明:∵,
∴∠ACD=∠BCE,
∵∠ADC=∠EBC,
∴△ACD∽△ECB;
(2)解:过B点作BH⊥CD于H点,如图,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ACB中,AB,
∵∠ACD=∠BCD=45°,
∴∠ABD=∠BAD=45°,
∴△ABD为等腰直角三角形,
∴BDAB,
在Rt△BCH中,
∵∠BCH=45°,
∴CH=BHBC,
在Rt△BDH中,DH,
∴CD=CH+DH2,
∵△ACD∽△ECB,
∴CA:CE=CD:CB,即3:CE=2:1,
解得CE,
即CE的长为.
7.【解答】(1)证明:∵BD是⊙O的直径,
∴∠BFD=90°,
∵∠C=90°,
∴∠BFD=∠C,
∵,
∴∠BEC=∠BDF,
∴△BCE∽△BDF,
∴,
∴BC DF=BF CE;
(2)解:连接DE,过E作EH⊥BD于H,如图:
∵∠C=90°,tan∠BFC,
∴,
∴BCCF,
∵∠A=∠CBF,
∴90°﹣∠A=90°﹣∠CBF,即∠ABC=∠BFC,
∴tan∠ABC=tan∠BFC,
∴,
∴ACBC(CF)=5CF,
∵AC﹣CF=AF=4,
∴5CF﹣CF=4,
∴CF,
∴BCCF=5,AC=5CF=5,
∴AB5,
由(1)知△BCE∽△BDF,
∴∠CBE=∠DBF,
∴∠CBE﹣∠FBE=∠DBF﹣∠FBE,即∠CBF=∠EBA,
∵∠A=∠CBF,
∴∠A=∠EBA,
∴AE=BE,
∴BH=AHAB,
∵∠BEH=90°﹣∠EBA=90°﹣∠CBF=∠BFC,
∴tan∠BEH=tan∠BFC,
∴,即,
∴EH,
∵BD是⊙O的直径,
∴∠BED=90°,
∴∠EDH=90°﹣∠DEH=∠BEH,
∴tan∠EDH=tan∠BEH,
∴,即,
∴DH,
∴BD=DH+BH3,
∴⊙O的直径为3.
答:CF的长为,⊙O的直径为3.
8.【解答】解:(1)AE与⊙O相切,理由如下:
如图,连接OA,
∵DA AC=DC AB,
∴,
∵BC是⊙O的直径,
∴∠BAC=90°=∠ADC,
∴△ABC∽△DAC,
∴∠ACB=∠ACD,
∵OA=OC,
∴∠OAC=∠ACB=∠ACD,
∴OA∥CD,
∴∠OAE=∠CDE=90°,
∴OA⊥DE,
又∵OA为半径,
∴AE与⊙O相切;
(2)如图,∵OA∥CD,
∴△AOE∽△DCE,
∴,
设BO=OC=OA=a,则BC=2a,
∵BC=BE=2a,
∴S△ABE=S△ABC,EO=3a,EC=4a,
∴,
∴CDa,
∵△ABC∽△DAC,
∴,
∴AC2=BC CDa2,
∵△ABC∽△DAC,
∴()2,
∴S2S1,
∴m.
9.【解答】(1)证明:∵AB为直径,
∴∠ACB=90°,
∵BE⊥CD,
∴∠BED=90°,
∵ 所对的圆周角为∠BDE和∠BAC,
∴∠BDE=∠BAC,
∴△DBE∽△ABC;
(2)解:如图,过点C作CG⊥AB,垂足为G,
∵∠ACB=90°,AC,BC=2,
∴AB5,
∵CG⊥AB,
∴AG=ACcosA1,
∵AF=2,
∴FG=AG=1,
∴CG是AF的垂直平分线,
∴AC=FC,
∴∠CAF=∠CFA=∠BFD=∠BDF,
∴BD=BF=AB﹣AF=5﹣2=3,
∵△DBE∽△ABC,
∴,
∴,
∴ED.
10.【解答】(1)证明:∵EH⊥AC于点H,AC是⊙O的直径,
∴∠AHE=∠AEC=90°,
∵∠HAE=∠EAC,
∴△HAE∽△EAC,
∴,
∴AE2=AH AC,
∵∠HAF=∠DAC,∠AHF=∠ADC=90°,
∴△AHF∽△ADC,
∴,
∴AH AC=AF AD,
∴AE2=AF AD.
(2)解:连接BC,
∵∠ADC的平分线交⊙O于点B,
∴∠ADB=∠CDB,
∴,
∴AB=BC=5,
∵∠ABC=90°,
∴AC5,
∵∠ACD=∠ABD,
∴sin∠ACD=sin∠ABD,
∴ADAC52,
∴AD的长是2.
11.【解答】(1)证明:∵AM是⊙O的切线,
∴∠BAM=90°,
∵∠CEA=90°,
∴AM∥CD,
∴∠CDB=∠APB,
∵∠CAB=∠CDB,
∴∠CAB=∠APB.
(2)解:如图,连接AD,
∵AB是直径,
∴∠CDB+∠ADC=90°,
∵∠CAB+∠C=90°,∠CDB=∠CAB,
∴∠ADC=∠C,
∴AD=AC=8,
∵AB=10,
∴BD=6,
∵∠BAD+∠DAP=90°,∠PAD+∠APD=90°,
∴∠APB=∠DAB,
∵∠BDA=∠BAP
∴△ADB∽△PAB,
∴,
∴PB,
∴DP6.
故答案为:.
12.【解答】(1)证明:连接OE,
∵四边形ODEF是平行四边形,
∴EF∥OD,EF=OD,
∵OA=OD,
∴EF∥OA,EF=OA,
∴四边形AOEF是平行四边形,
∴OE∥AC,
∴∠OEB=∠ACB,
∵∠ACB=90°,
∴∠OEB=90°,
∴OE⊥BC,
∵OE是⊙O的半径,
∴BC与⊙O相切;
(2)解:过点F作FH⊥OA于点H,
∵四边形AOEF是平行四边形,
∴EF∥OA,
∴∠CFE=∠CAB,
∴sin∠CFE=sin∠CAB,
在Rt△CEF中,∠ACB=90°,
∵CE=6,sin∠CFE,
∴EF,
∵四边形AOEF是平行四边形,且OA=OE,
∴ AOEF是菱形,
∴AF=AO=EF=10,
在Rt△AFH中,∠AHF=90°,
∵AF=10,sin∠CAB,
∴FH=AF,
∵AH2=AF2﹣FH2,
∴AH,
∴OH=AO﹣AH=10﹣8=2,
在Rt△OFH中,∠FHO=90°,
∵OF2=OH2+FH2,
∴OF,
∴OF=2.
13.【解答】(1)证明:连接AC,
∵AB为直径,
∴∠ACB=∠ACE=90°,
又∵点C是的中点
∴∠CAE=∠CAB,CD=CB,
又∵AC=AC
∴△ACE≌△ACB(ASA),
∴CE=CB,
∴CE=CD;
(2)解:∵△ACE≌△ACB,AB=3,
∴AE=AB=3,
又∵四边形ABCD内接于圆O,
∴∠ADC+∠ABC=180°,
又∵∠ADC+∠CDE=180°,
∴∠CDE=∠ABE,
又∵∠E=∠E,
∴△EDC∽△EBA,
∴,
即:,
解得:DE=2,
∴AD=AE﹣DE=1.
14.【解答】(1)证明:连接OD,CD,
∵∠ACB=90°,
∴∠ACD+∠DCB=90°,
∵OC=OD,
∴∠OCD=∠ODC,
∵AC是⊙O的直径,
∴∠ADC=90°,
∴∠CDB=180°﹣∠ADC=90°,
∵点E是边BC的中点,
∴DE=CEBC,
∴∠DCE=∠CDE,
∴∠ODC+∠CDE=90°,
∴∠ODE=90°,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)解:∵AD=4,BD=9,
∴AB=AD+BD=4+9=13,
∵∠ACB=∠ADC=90°,∠A=∠A,
∴△ACB∽△ADC,
∴,
∴AC2=AD AB=4×13=52,
∴AC=2,
∴⊙O的半径为.
15.【解答】(1)证明:连接OE,如图,
∵AC是⊙O的切线,
∴OE⊥AC.
∵AC⊥BC,
∴OE∥BC,
∴∠OED=∠F.
∵OD=OE,
∴∠ODE=∠OED,
∴∠BDE=∠F,
∴BD=BF;
(2)解:连接BE,如图,
∵∠BDE=∠F,
∴tan∠BDE=tan∠F=2,
∵CF=1,tan∠F,
∴CE=2.
∵BD是⊙O直径,
∴∠BED=90°,
∴BE⊥EF.
∵EC⊥BF,
∴△ECF∽△BCE,
∴,
∴EC2=BC CF.
∴BC=4.
∴BF=BC+CF=5.
∴BD=BF=5,
即⊙O的直径为5.
21世纪教育网(www.21cnjy.com)
同课章节目录
