北师大版2024—2025学年七年级下册数学期中考试全真模拟试卷(含答案)
文档属性
| 名称 | 北师大版2024—2025学年七年级下册数学期中考试全真模拟试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 876.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 19:27:18 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
北师大版2024—2025学年七年级下册数学期中考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.花粉的质量很小,一粒某种植物花粉的质量约为0.000037mg,那么0.000037可用科学记数法表示为( )
A.3.7×10﹣5 B.3.7×10﹣6 C.3.7×10﹣7 D.3.7×10﹣8
2.计算:0.252024×(﹣4)2025=( )
A.﹣4 B.﹣1 C.1 D.4
3.如果等式x2+mx﹣6=(x+3)(x+n)成立,那么m和n的值分别是( )
A.m=1,n=2 B.m=1,n=﹣2 C.m=﹣1,n=2 D.m=﹣1,n=﹣2
4.若2x﹣3y+z﹣2=0,则16x÷82y×4z的值为( )
A.16 B.﹣16 C.8 D.4
5.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. B. C. D.
6.下列不能用平方差公式运算的是( )
A.(﹣x+2)(﹣x﹣2) B.(﹣2m﹣n)(﹣2m﹣n)
C.(﹣2a+b)(2a+b) D.(y﹣x)(﹣x﹣y)
7.已知a、b是常数,若化简(x﹣a)(2x2+bx﹣4)的结果不含x的二次项,则12a﹣6b﹣1的值为( )
A.1 B.﹣1 C.5 D.﹣13
8.如表是一位同学在罚球线上投篮的试验结果,根据表中数据回答下列问题:
投篮次数(n) 50 100 150 200 250 300 500
投中次数(m) 28 60 78 104 124 153 252
估计这位同学投篮一次,投中的概率约是( )(精确到0.1)
A.0.4 B.0.5 C.0.55 D.0.6
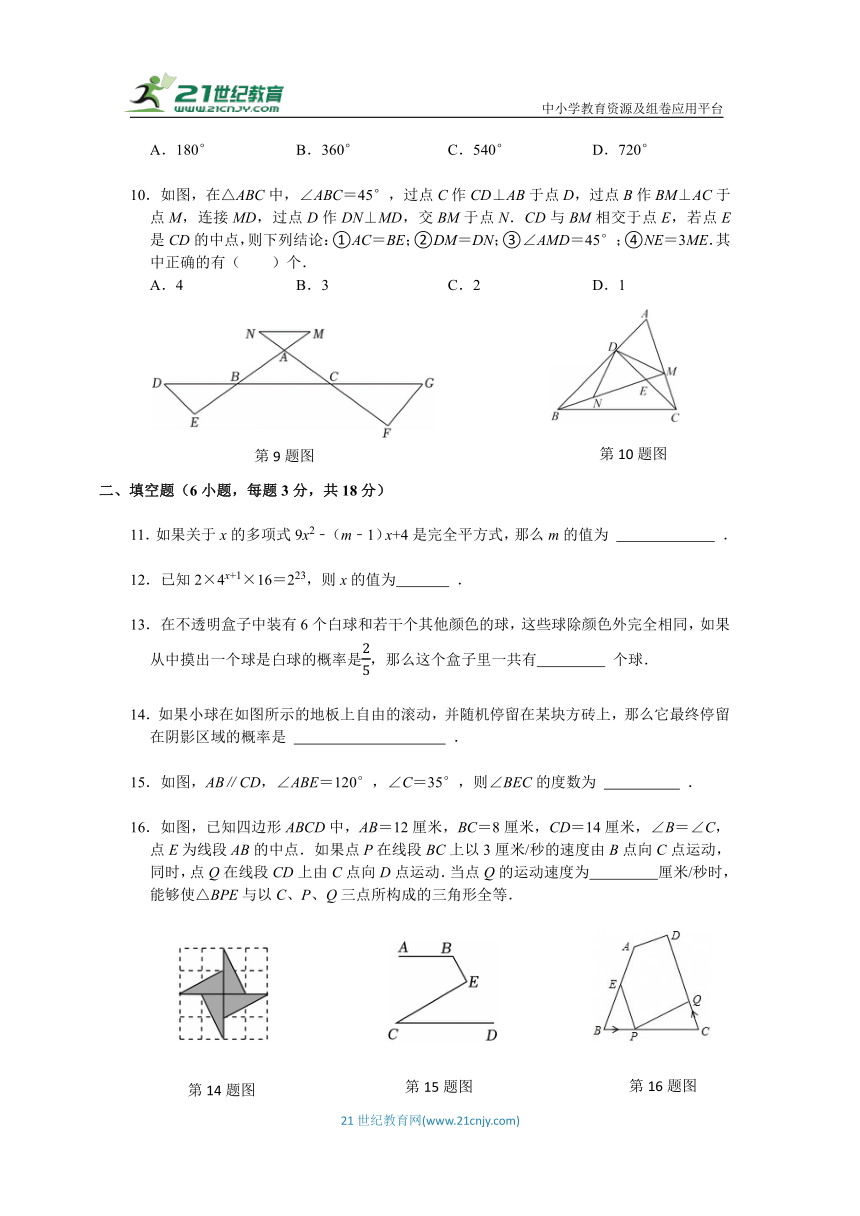
9.如图,线段DG,EM,FN两两相交于B,C,A三点 则∠D+∠E+∠F+∠G+∠M+∠N的度数是( )
A.180° B.360° C.540° D.720°
10.如图,在△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,连接MD,过点D作DN⊥MD,交BM于点N.CD与BM相交于点E,若点E是CD的中点,则下列结论:①AC=BE;②DM=DN;③∠AMD=45°;④NE=3ME.其中正确的有( )个.
A.4 B.3 C.2 D.1
二、填空题(6小题,每题3分,共18分)
11.如果关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,那么m的值为 .
12.已知2×4x+1×16=223,则x的值为 .
在不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,如果从中摸出一个球是白球的概率是,那么这个盒子里一共有 个球.
14.如果小球在如图所示的地板上自由的滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
15.如图,AB∥CD,∠ABE=120°,∠C=35°,则∠BEC的度数为 .
16.如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
第II卷
北师大版2024—2025学年七年级下册数学期中考试全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值,其中.
18.计算:.
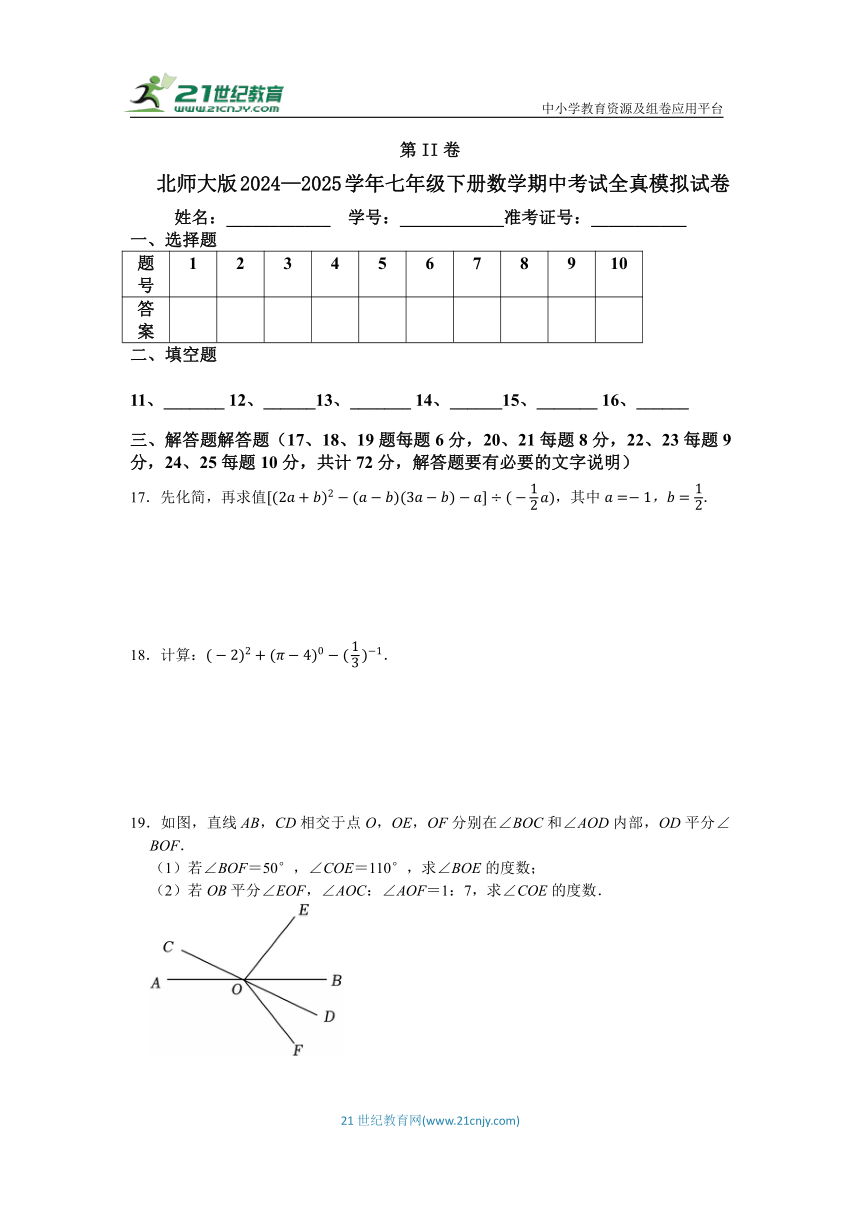
19.如图,直线AB,CD相交于点O,OE,OF分别在∠BOC和∠AOD内部,OD平分∠BOF.
(1)若∠BOF=50°,∠COE=110°,求∠BOE的度数;
(2)若OB平分∠EOF,∠AOC:∠AOF=1:7,求∠COE的度数.
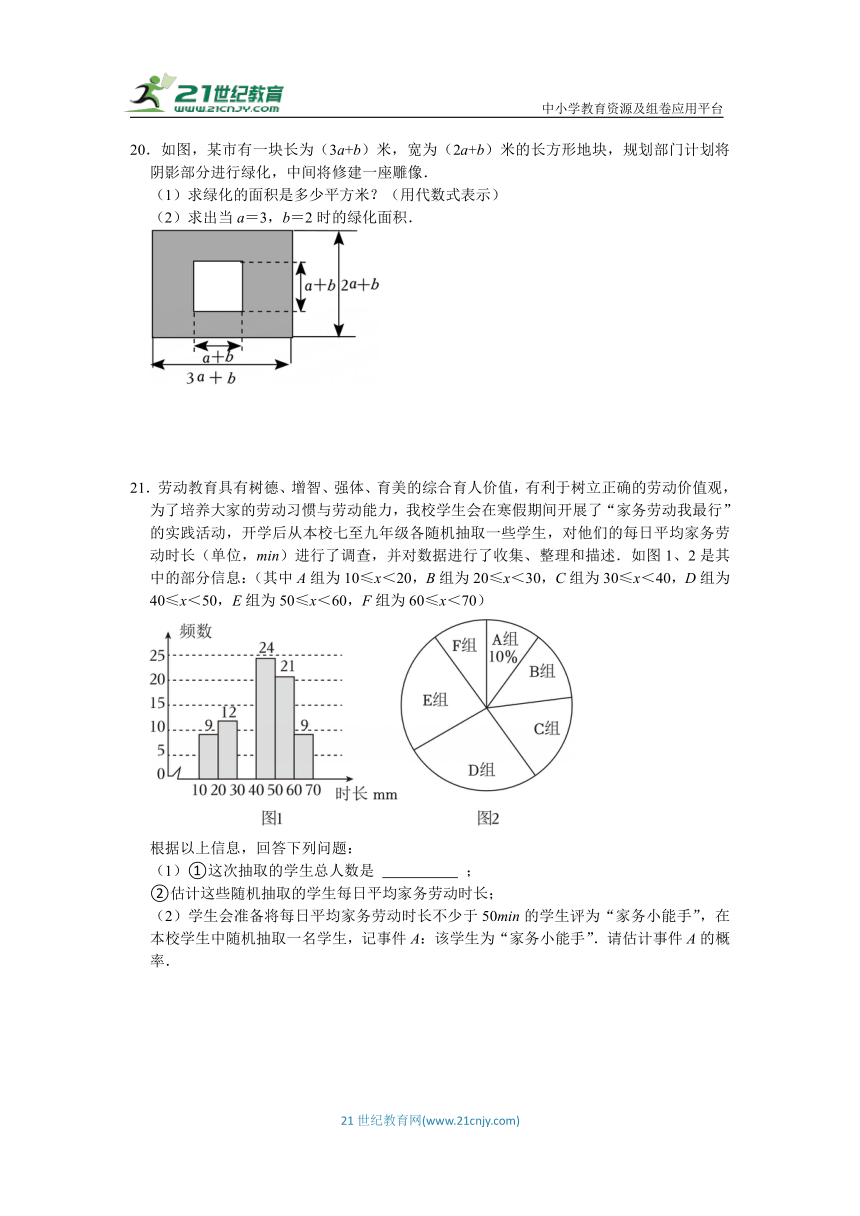
20.如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)求绿化的面积是多少平方米?(用代数式表示)
(2)求出当a=3,b=2时的绿化面积.
21.劳动教育具有树德、增智、强体、育美的综合育人价值,有利于树立正确的劳动价值观,为了培养大家的劳动习惯与劳动能力,我校学生会在寒假期间开展了“家务劳动我最行”的实践活动,开学后从本校七至九年级各随机抽取一些学生,对他们的每日平均家务劳动时长(单位,min)进行了调查,并对数据进行了收集、整理和描述.如图1、2是其中的部分信息:(其中A组为10≤x<20,B组为20≤x<30,C组为30≤x<40,D组为40≤x<50,E组为50≤x<60,F组为60≤x<70)
根据以上信息,回答下列问题:
(1)①这次抽取的学生总人数是 ;
②估计这些随机抽取的学生每日平均家务劳动时长;
(2)学生会准备将每日平均家务劳动时长不少于50min的学生评为“家务小能手”,在本校学生中随机抽取一名学生,记事件A:该学生为“家务小能手”.请估计事件A的概率.
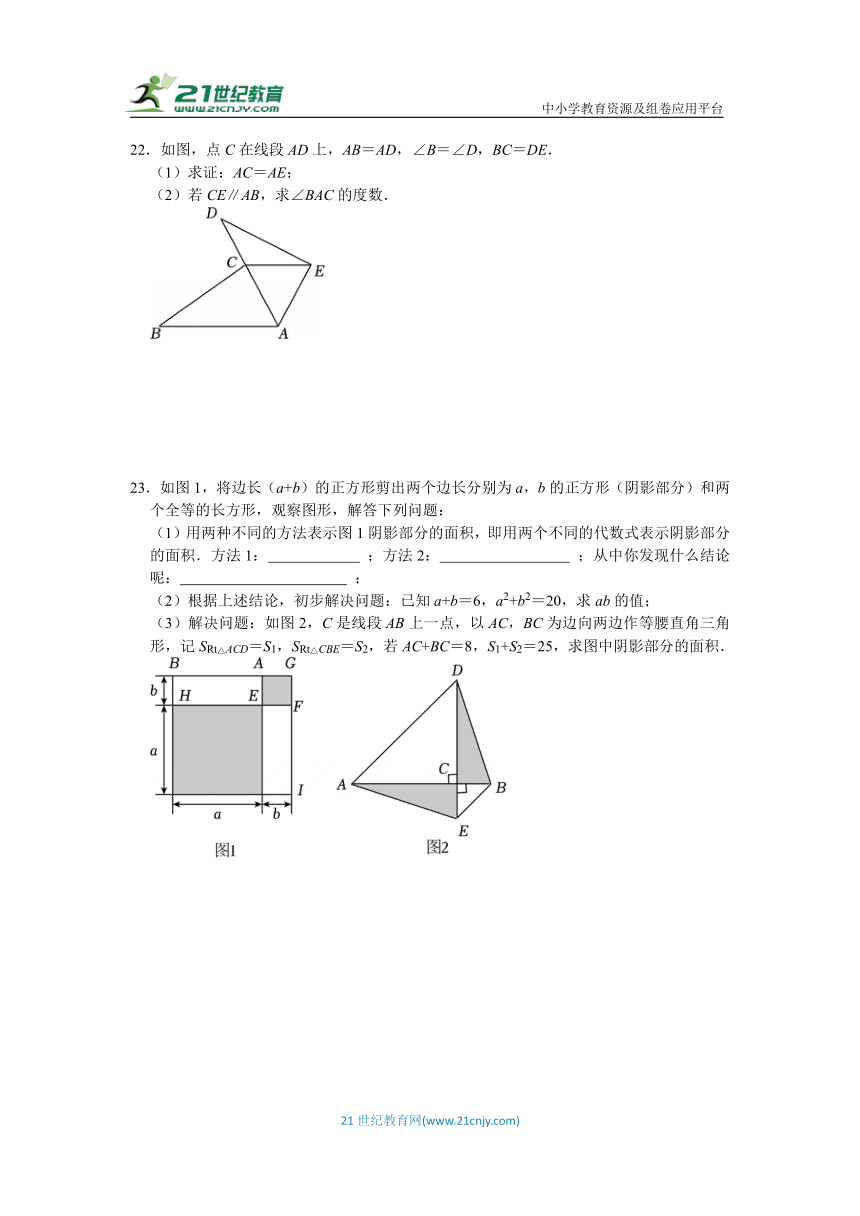
22.如图,点C在线段AD上,AB=AD,∠B=∠D,BC=DE.
(1)求证:AC=AE;
(2)若CE∥AB,求∠BAC的度数.
23.如图1,将边长(a+b)的正方形剪出两个边长分别为a,b的正方形(阴影部分)和两个全等的长方形,观察图形,解答下列问题:
(1)用两种不同的方法表示图1阴影部分的面积,即用两个不同的代数式表示阴影部分的面积.方法1: ;方法2: ;从中你发现什么结论呢: ;
(2)根据上述结论,初步解决问题:已知a+b=6,a2+b2=20,求ab的值;
(3)解决问题:如图2,C是线段AB上一点,以AC,BC为边向两边作等腰直角三角形,记SRt△ACD=S1,SRt△CBE=S2,若AC+BC=8,S1+S2=25,求图中阴影部分的面积.
24.如图所示,AB∥CD,点E,F分别在直线CD,AB上,∠BEC=2∠BEF,过点A作AG⊥BE的延长线交于点G,交CD于点N,AK平分∠BAG,交EF于点H,交BE于点M.
(1)直接写出∠AHE,∠FAH,∠KEH之间的关系: .
(2)若,求∠AHE.
(3)在(2)的条件下,将△KHE绕着点E以每秒3°的速度逆时针旋转,旋转时间为t,当KE边与射线ED重合时停止,则在旋转过程中,当△KHE的其中一边与△ENG的某一边平行时,求此时t的值.
25.在Rt△ABC中,∠A=90°,∠C=30°,BD为△ABC的角平分线,点E,F分别在边AB,BC上,∠EDF=120°.
(1)如图1,求证:DE=DF;
(2)如图2,∠CDF=45°,连接EF,EF与BD交于点G.猜想AE与DG之间的数量关系,并说明理由;
(3)在(2)的条件下,若,求证:.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B A B B B. B B A
1.【解答】解:0.000037=3.7×10﹣5.
故选:A.
2.【解答】解:原式
=(﹣4)2024×(﹣4)
=(﹣1)2024×(﹣4)
=1×(﹣4)
=﹣4,
故选:A.
3.【解答】解:∵x2+mx﹣6=(x+3)(x+n)=x2+(3+n)x+3n,
∴m=3+n,3n=﹣6,
∴n=﹣2,m=1,
故选:B.
4.【解答】解:∵2x﹣3y+z﹣2=0,
∴2x﹣3y+z=2,
则原式=(24)x÷(23)2y×(22)z
=24x÷26y×22z
=22(2x﹣3y+z)
=24
=16,
故选:A.
5.【解答】解:A、∠1=∠2不能判定任何直线平行,故本选项错误;
B、∵∠1=∠2,∴AB∥CD,符合平行线的判定定理,故本选项正确;
C、∵∠1=∠2,∴AC∥BD,故本选项错误;
D、∠1=∠2不能判定任何直线平行,故本选项错误.
故选:B.
6.【解答】解:A、(﹣x+2)(﹣x﹣2)=(﹣x)2﹣4=x2﹣4,故A不符合题意;
B、(﹣2m﹣n)(﹣2m﹣n)=(﹣2m﹣n)2=(2m+n)2=4m2+4mn+n2,故B符合题意;
C、(﹣2a+b)(2a+b)=b2﹣(2a)2=b2﹣4a2,故C不符合题意;
D、(y﹣x)(﹣x﹣y)=(﹣x)2﹣y2=x2﹣y2,故D不符合题意;
故选:B.
7.【解答】解:∵多项式(x﹣a)(2x2+bx﹣4)=2x3+(﹣2a+b)x2+(﹣ab﹣4)x+4a不含x的二次项,
∴﹣2a+b=0,
解得b=2a,
∴12a﹣6b﹣1=12a﹣6×2a﹣1=﹣1.
故选:B.
8.【解答】解:根据题意得:
28÷50=0.56,
60÷100=0.6,
78÷150=0.52,
104÷200=0.52,
124÷250=0.496,
153÷300=0.51,
252÷500=0.504,
由此,估计这位同学投篮一次,投中的概率约是0.5,
故选:B.
9.【解答】解:在△ABC和△CGF中,
∵∠ACB=∠GCF,
∴∠G+∠F=∠ABC+∠BAC;
在△ABC和△ANM中,
∵∠BAC=∠MAN,
∴∠M+∠N=∠ABC+∠ACB;
在△ABC和△BDE中,
∵∠ABC=∠DBE,
∴∠D+∠E=∠ACB+∠BAC,
∴∠D+∠E+∠F+∠G+∠M+∠N
=(∠ACB+∠BAC)+(∠ABC+∠BAC)+(∠ABC+∠ACB)
=2(∠ABC+∠BAC+∠ACB)
=2×180°
=360°.
故选:B.
10.【解答】证:∵CD⊥AB,BM⊥AC,
∴∠BDE=∠CME=90°,
∵∠DEB=∠MEC,
∴∠DBE=∠DCA,
∵∠ABC=45°,CD⊥AB,
∴△BDC是等腰直角三角形,
∴BD=CD,
∵∠BDE=∠CDA,∠DBE=∠DCA,
∴△BDE≌△CDA(ASA),
∴BE=AC,
∵∠BDC=∠NDM=90°,
∴∠BDN=∠CDM,
∵∠DBN=∠DCM,BD=CD,
∴△BDN≌△CDM(ASA),
∴DM=DN,
∵∠NDM=90°,
∴△DNM是等腰直角三角形,
∴∠DMN=45°,
∴∠AMD=45°,
故①②③正确,
过点D作DF⊥MN于点F,则∠DFE=∠CME=90°,
∵DN⊥MD,DN=DM,
∴MN=2FM=2FN,
∵点E是CD的中点,
∴DE=CE,
∵∠DEF=∠CEM,∠DFE=∠CME,
∴△DEF≌△CEM(AAS),
∴ME=EF,
∴MN=2MF=4ME,
∴NE=3ME,
故④正确,
本题选:A.
二、填空题
11.【解答】解:∵关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,
∴9x2﹣(m﹣1)x+4=(3x±2)2,
∴﹣(m﹣1)=±12,即m﹣1=±12,
解得:m=13或﹣11,
故答案为:13或﹣11.
12.【解答】解:∵2×4x+1×16
=2×22x+2×24
=22x+7
=223,
∴2x+7=23,
∴x=8.
故答案为:8.
13.【解答】解:∵不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,摸出一个球是白球的概率是,
∴白球占小球总数的,
∴这个盒子里一共有(个).
故答案为:15.
14.【解答】解:∵总面积为16个小正方形的面积,
如图所示,阴影部分的面积为4个由两个小正方形组成的长方形的一半,
∴阴影部分的面积为4个小正方形的面积,
∴小球停留在阴影区域的概率是,
故答案为:.
15.【解答】解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BEF=180°﹣∠ABE=60°,∠CEF=∠C=35°,
∴∠BEC=∠BEF+∠CEF=95°;
故答案为:95°.
16.【解答】解:设点P运动的时间为t秒,则BP=3t,CP=8﹣3t,
∵∠B=∠C,
∴①当BE=CP=6,BP=CQ时,△BPE与△CQP全等,
此时,6=8﹣3t,
解得t,
∴BP=CQ=2,
此时,点Q的运动速度为23厘米/秒;
②当BE=CQ=6,BP=CP时,△BPE与△CQP全等,
此时,3t=8﹣3t,
解得t,
∴点Q的运动速度为6厘米/秒;
故答案为:3或.
三、解答题
17.【解答】解:
=(4a2+4ab+b2﹣3a2+4ab﹣b2﹣a)÷(a)
=(a2+8ab﹣a)÷(a)
=﹣2a﹣16b+2,
当时,原式=﹣2×(﹣1)﹣162
=2﹣8+2
=﹣4.
18.【解答】解:原式=4+1﹣3
=5﹣3
=2.
19.【解答】解:(1)∵OD平分∠BOF,
∴,
∵∠COE+∠BOE+∠BOD=180°,
∴∠BOE=180°﹣110°﹣25°=45°;
(2)设∠AOC=x,∠AOF=7x,
∴∠AOC=∠BOD=x,
∵OD平分∠BOF,
∴,
∵∠AOC+∠AOF+∠FOD=180°,
∴x+7x+x=180°,
解得:x=20°,
∴∠BOD=∠FOD=20°,
∴∠BOF=20°×2=40°,
∵OB平分∠EOF,
∴∠EOB=∠BOF=40°,
∵∠COE+∠EOB+∠BOD=180°,
∴∠COE=180°﹣40°﹣20°=120°.
20.【解答】解:(1)阴影部分的面积=(3a+b)(2a+b)﹣(a+b)2
=6a2+5ab+b2﹣a2﹣2ab﹣b2
=5a2+3ab;
(2)当a=3,b=2时,原式=5×32+3×3×2=63(平方米).
21.【解答】解:(1)①这次抽取的学生总人数是9÷10%=90(人);
②C组人数为90﹣(9+12+24+21+9)=15(人),
则这些随机抽取的学生每日平均家务劳动时长约为(15×9+25×12+35×15+45×24+55×21+65×9)=42(min);
故答案为:90人;
(2)在本校学生中随机抽取一名学生,记事件A:该学生为“家务小能手”.
则事件A的概率约为.
22.【解答】(1)证明:在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS),
∴AC=AE.
(2)解:由(1)得△ABC≌△ADE,
∴∠BAC=∠DAE,
∵点C在线段AD上,
∴∠BAC=∠DAE,即∠BAC=∠CAE,
∵AC=AE,
∴∠ACE=∠AEC,
∵CE∥AB,
∴∠BAC=∠ACE,
∴∠CAE=∠ACE=∠AEC180°=60°,
∴∠BAC=∠CAE=60°,
∴∠BAC的度数是60°.
23.【解答】解:(1)方法1:根据题意可知,阴影部分面积为边长为a和边长为b的正方形面积之和,
∴;
方法2:根据题意可知,阴影部分面积为边长为(a+b)的正方形面积减去长为a,宽为b的长方形面积×2,
∴,
根据阴影部分面积相等可知:a2+b2=(a+b)2﹣2ab.
故答案为:a2+b2;(a+b)2﹣2ab;a2+b2=(a+b)2﹣2ab;
(2)∵a+b=6,a2+b2=20,
由(1)得:a2+b2=(a+b)2﹣2ab,
∴;
(3)设AC=x,BC=y,
∵AC+BC=8,S1+S2=25,
∴,
∴,
∴阴影部分的面积为.
24.【解答】解:(1)∵AB∥CD,
∴∠KEH=∠AFH,
∵∠AHE是△AHF的外角,
∴∠AHE=∠AFH+∠FAH,
∴∠AHE=∠FAH+∠KEH,
故答案为:∠AHE=∠FAH+∠KEH;
(2)∵AB∥CD,
∴∠BAK=∠MKE,∠ABE=∠BEC,
∵,
∴∠BAK=2∠BEF,
∵∠BEC=2∠BEF,
∴∠BAK=∠BEC,
∴∠BAK=∠ABE,
∵AK平分∠BAG,
∴∠BAK=∠ABE=∠GAK,
∵AG⊥BE,
∴∠AGB=90°,
∴3∠BAK=90°,
∴∠BAK=∠ABE=∠GAK=30°,
∴,
∴∠CEF=45°,
∴∠CEF=∠AFE=45°,
∴∠AHE=∠AFE+∠BAK=45°+30°=75°;
(3)①当KH∥NG时,延长KE交GN边于P,如图,
∵∠EKH=∠EPG=30°,
∴∠PEG=90°﹣∠EPG=60°,
∵∠GEN=90°﹣∠ENG=30°,
∴∠PEN=∠PEG﹣∠GEN=30°,
∴∠CEK=∠PEN=30°,
当△KHE绕E点旋转30°时,EK∥GN,
(秒);
②当KH∥EG时,如图,
∴∠EKH=∠KEG=30°,∠NEK=∠NEG+∠KEG=60°,
∴∠CEK=120°,
当△KHE绕点E旋转120°时,KH∥EG,
∴(秒);
③当KH∥EN时,即EK与EG在同一直线上时,
∴∠CEK=150°,
当△KHE绕点E旋转150°时,KH∥EN,
∴(秒);
④当KE∥NG时,
∵∠GEK=30°,
∴∠CEK=90°﹣∠GEK=60°,
当△KHE旋转60°时,KE∥NG,
∴(秒)
⑤当HE∥NG时,
∵∠GEK=30°,∠KEH=45°,
∴∠CEK=∠CEH+∠HEK=90°﹣∠GEK+∠HEK=105°,
∴当△KHE旋转105°时,HE∥NG,
∴(秒),
综上所述,当△KHE的其中一边与△ENG的某一边平行时,t的值为10,40,50,20,35.
25.【解答】(1)证明:过D作DM⊥BC.
∵BD为△ABC的角平分线,
∴DM=DA.
∵∠C=30°,
∴∠MDF+∠FDC=60°,
∵∠EDF=120°,
∴∠ADE+∠FDC=60°,
∴∠ADE=∠MDF.
在△AED和△MDF中,
,
∴△AED≌△MDF(AAS),
∴DE=DF.
(2)过F作FQ⊥GD,过D作DM⊥BC.
由(1)知△AED≌△MDF,
∴MF=AE,∠MDF=∠ADE,
∵∠EDF=∠EDM+∠MDF=120°,
∴∠EDM+∠ADE=120°,
∠ADM=120°,
∵∠A=∠DMB=90°,∠ABD=∠DBM,
∴∠ADB=∠BDM,
∵∠ADB+∠BDM=∠ADM=120°,
∴∠ADB=∠BDM=60°,
∵∠FDC=45°,∠EDF=120°,
∴∠ADE=15°,
∴∠EDG=60°﹣15°=45°.
∴∠GDF=120°﹣45°=75°.
∵∠EDF=120°,DE=DF,
∴∠DEG=∠DFG=30°,
∴∠FGD=75°,
∴∠FDG=∠FGD,
∴FG=FD,
∴GD=2QD.
在△FQD和△DMF中,
,
∴△FQD≌△DMF(AAS),
∴QD=MF,
∴DG=2AE.
(3)过E作EN⊥BDD,过F作FH⊥BD,过D作DM⊥BC,DR⊥EF.
由(2)∠AED=90°﹣∠ADE=75°,
∴∠BEG=180°﹣∠AED﹣∠DEG=75°,
又∠EGB=∠DGF=75°,
∴∠BEG=∠BGE,
∴BE=BG,
同理:FG=FD.
∴.
设BE=mx,BF=nx,
∵∠BEG=∠BGE=75°,
∴BG=BE=mx,
同理:BD=BF=nx,
∴GD=BD﹣BG=nx﹣mx=(n﹣m)x,
∴.
21世纪教育网(www.21cnjy.com)
北师大版2024—2025学年七年级下册数学期中考试全真模拟试卷
考生注意:本试卷共三道大题,25道小题,满分120分,时量120分钟
第I卷
一、选择题(每题只有一个正确选项,每小题3分,满分30分)
1.花粉的质量很小,一粒某种植物花粉的质量约为0.000037mg,那么0.000037可用科学记数法表示为( )
A.3.7×10﹣5 B.3.7×10﹣6 C.3.7×10﹣7 D.3.7×10﹣8
2.计算:0.252024×(﹣4)2025=( )
A.﹣4 B.﹣1 C.1 D.4
3.如果等式x2+mx﹣6=(x+3)(x+n)成立,那么m和n的值分别是( )
A.m=1,n=2 B.m=1,n=﹣2 C.m=﹣1,n=2 D.m=﹣1,n=﹣2
4.若2x﹣3y+z﹣2=0,则16x÷82y×4z的值为( )
A.16 B.﹣16 C.8 D.4
5.下列图形中,由∠1=∠2能得到AB∥CD的是( )
A. B. C. D.
6.下列不能用平方差公式运算的是( )
A.(﹣x+2)(﹣x﹣2) B.(﹣2m﹣n)(﹣2m﹣n)
C.(﹣2a+b)(2a+b) D.(y﹣x)(﹣x﹣y)
7.已知a、b是常数,若化简(x﹣a)(2x2+bx﹣4)的结果不含x的二次项,则12a﹣6b﹣1的值为( )
A.1 B.﹣1 C.5 D.﹣13
8.如表是一位同学在罚球线上投篮的试验结果,根据表中数据回答下列问题:
投篮次数(n) 50 100 150 200 250 300 500
投中次数(m) 28 60 78 104 124 153 252
估计这位同学投篮一次,投中的概率约是( )(精确到0.1)
A.0.4 B.0.5 C.0.55 D.0.6
9.如图,线段DG,EM,FN两两相交于B,C,A三点 则∠D+∠E+∠F+∠G+∠M+∠N的度数是( )
A.180° B.360° C.540° D.720°
10.如图,在△ABC中,∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM⊥AC于点M,连接MD,过点D作DN⊥MD,交BM于点N.CD与BM相交于点E,若点E是CD的中点,则下列结论:①AC=BE;②DM=DN;③∠AMD=45°;④NE=3ME.其中正确的有( )个.
A.4 B.3 C.2 D.1
二、填空题(6小题,每题3分,共18分)
11.如果关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,那么m的值为 .
12.已知2×4x+1×16=223,则x的值为 .
在不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,如果从中摸出一个球是白球的概率是,那么这个盒子里一共有 个球.
14.如果小球在如图所示的地板上自由的滚动,并随机停留在某块方砖上,那么它最终停留在阴影区域的概率是 .
15.如图,AB∥CD,∠ABE=120°,∠C=35°,则∠BEC的度数为 .
16.如图,已知四边形ABCD中,AB=12厘米,BC=8厘米,CD=14厘米,∠B=∠C,点E为线段AB的中点.如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.当点Q的运动速度为 厘米/秒时,能够使△BPE与以C、P、Q三点所构成的三角形全等.
第II卷
北师大版2024—2025学年七年级下册数学期中考试全真模拟试卷
姓名:____________ 学号:____________准考证号:___________
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案
二、填空题
11、_______ 12、______13、_______ 14、______15、_______ 16、______
三、解答题解答题(17、18、19题每题6分,20、21每题8分,22、23每题9分,24、25每题10分,共计72分,解答题要有必要的文字说明)
17.先化简,再求值,其中.
18.计算:.
19.如图,直线AB,CD相交于点O,OE,OF分别在∠BOC和∠AOD内部,OD平分∠BOF.
(1)若∠BOF=50°,∠COE=110°,求∠BOE的度数;
(2)若OB平分∠EOF,∠AOC:∠AOF=1:7,求∠COE的度数.
20.如图,某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像.
(1)求绿化的面积是多少平方米?(用代数式表示)
(2)求出当a=3,b=2时的绿化面积.
21.劳动教育具有树德、增智、强体、育美的综合育人价值,有利于树立正确的劳动价值观,为了培养大家的劳动习惯与劳动能力,我校学生会在寒假期间开展了“家务劳动我最行”的实践活动,开学后从本校七至九年级各随机抽取一些学生,对他们的每日平均家务劳动时长(单位,min)进行了调查,并对数据进行了收集、整理和描述.如图1、2是其中的部分信息:(其中A组为10≤x<20,B组为20≤x<30,C组为30≤x<40,D组为40≤x<50,E组为50≤x<60,F组为60≤x<70)
根据以上信息,回答下列问题:
(1)①这次抽取的学生总人数是 ;
②估计这些随机抽取的学生每日平均家务劳动时长;
(2)学生会准备将每日平均家务劳动时长不少于50min的学生评为“家务小能手”,在本校学生中随机抽取一名学生,记事件A:该学生为“家务小能手”.请估计事件A的概率.
22.如图,点C在线段AD上,AB=AD,∠B=∠D,BC=DE.
(1)求证:AC=AE;
(2)若CE∥AB,求∠BAC的度数.
23.如图1,将边长(a+b)的正方形剪出两个边长分别为a,b的正方形(阴影部分)和两个全等的长方形,观察图形,解答下列问题:
(1)用两种不同的方法表示图1阴影部分的面积,即用两个不同的代数式表示阴影部分的面积.方法1: ;方法2: ;从中你发现什么结论呢: ;
(2)根据上述结论,初步解决问题:已知a+b=6,a2+b2=20,求ab的值;
(3)解决问题:如图2,C是线段AB上一点,以AC,BC为边向两边作等腰直角三角形,记SRt△ACD=S1,SRt△CBE=S2,若AC+BC=8,S1+S2=25,求图中阴影部分的面积.
24.如图所示,AB∥CD,点E,F分别在直线CD,AB上,∠BEC=2∠BEF,过点A作AG⊥BE的延长线交于点G,交CD于点N,AK平分∠BAG,交EF于点H,交BE于点M.
(1)直接写出∠AHE,∠FAH,∠KEH之间的关系: .
(2)若,求∠AHE.
(3)在(2)的条件下,将△KHE绕着点E以每秒3°的速度逆时针旋转,旋转时间为t,当KE边与射线ED重合时停止,则在旋转过程中,当△KHE的其中一边与△ENG的某一边平行时,求此时t的值.
25.在Rt△ABC中,∠A=90°,∠C=30°,BD为△ABC的角平分线,点E,F分别在边AB,BC上,∠EDF=120°.
(1)如图1,求证:DE=DF;
(2)如图2,∠CDF=45°,连接EF,EF与BD交于点G.猜想AE与DG之间的数量关系,并说明理由;
(3)在(2)的条件下,若,求证:.
参考答案
一、选择题
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B A B B B. B B A
1.【解答】解:0.000037=3.7×10﹣5.
故选:A.
2.【解答】解:原式
=(﹣4)2024×(﹣4)
=(﹣1)2024×(﹣4)
=1×(﹣4)
=﹣4,
故选:A.
3.【解答】解:∵x2+mx﹣6=(x+3)(x+n)=x2+(3+n)x+3n,
∴m=3+n,3n=﹣6,
∴n=﹣2,m=1,
故选:B.
4.【解答】解:∵2x﹣3y+z﹣2=0,
∴2x﹣3y+z=2,
则原式=(24)x÷(23)2y×(22)z
=24x÷26y×22z
=22(2x﹣3y+z)
=24
=16,
故选:A.
5.【解答】解:A、∠1=∠2不能判定任何直线平行,故本选项错误;
B、∵∠1=∠2,∴AB∥CD,符合平行线的判定定理,故本选项正确;
C、∵∠1=∠2,∴AC∥BD,故本选项错误;
D、∠1=∠2不能判定任何直线平行,故本选项错误.
故选:B.
6.【解答】解:A、(﹣x+2)(﹣x﹣2)=(﹣x)2﹣4=x2﹣4,故A不符合题意;
B、(﹣2m﹣n)(﹣2m﹣n)=(﹣2m﹣n)2=(2m+n)2=4m2+4mn+n2,故B符合题意;
C、(﹣2a+b)(2a+b)=b2﹣(2a)2=b2﹣4a2,故C不符合题意;
D、(y﹣x)(﹣x﹣y)=(﹣x)2﹣y2=x2﹣y2,故D不符合题意;
故选:B.
7.【解答】解:∵多项式(x﹣a)(2x2+bx﹣4)=2x3+(﹣2a+b)x2+(﹣ab﹣4)x+4a不含x的二次项,
∴﹣2a+b=0,
解得b=2a,
∴12a﹣6b﹣1=12a﹣6×2a﹣1=﹣1.
故选:B.
8.【解答】解:根据题意得:
28÷50=0.56,
60÷100=0.6,
78÷150=0.52,
104÷200=0.52,
124÷250=0.496,
153÷300=0.51,
252÷500=0.504,
由此,估计这位同学投篮一次,投中的概率约是0.5,
故选:B.
9.【解答】解:在△ABC和△CGF中,
∵∠ACB=∠GCF,
∴∠G+∠F=∠ABC+∠BAC;
在△ABC和△ANM中,
∵∠BAC=∠MAN,
∴∠M+∠N=∠ABC+∠ACB;
在△ABC和△BDE中,
∵∠ABC=∠DBE,
∴∠D+∠E=∠ACB+∠BAC,
∴∠D+∠E+∠F+∠G+∠M+∠N
=(∠ACB+∠BAC)+(∠ABC+∠BAC)+(∠ABC+∠ACB)
=2(∠ABC+∠BAC+∠ACB)
=2×180°
=360°.
故选:B.
10.【解答】证:∵CD⊥AB,BM⊥AC,
∴∠BDE=∠CME=90°,
∵∠DEB=∠MEC,
∴∠DBE=∠DCA,
∵∠ABC=45°,CD⊥AB,
∴△BDC是等腰直角三角形,
∴BD=CD,
∵∠BDE=∠CDA,∠DBE=∠DCA,
∴△BDE≌△CDA(ASA),
∴BE=AC,
∵∠BDC=∠NDM=90°,
∴∠BDN=∠CDM,
∵∠DBN=∠DCM,BD=CD,
∴△BDN≌△CDM(ASA),
∴DM=DN,
∵∠NDM=90°,
∴△DNM是等腰直角三角形,
∴∠DMN=45°,
∴∠AMD=45°,
故①②③正确,
过点D作DF⊥MN于点F,则∠DFE=∠CME=90°,
∵DN⊥MD,DN=DM,
∴MN=2FM=2FN,
∵点E是CD的中点,
∴DE=CE,
∵∠DEF=∠CEM,∠DFE=∠CME,
∴△DEF≌△CEM(AAS),
∴ME=EF,
∴MN=2MF=4ME,
∴NE=3ME,
故④正确,
本题选:A.
二、填空题
11.【解答】解:∵关于x的多项式9x2﹣(m﹣1)x+4是完全平方式,
∴9x2﹣(m﹣1)x+4=(3x±2)2,
∴﹣(m﹣1)=±12,即m﹣1=±12,
解得:m=13或﹣11,
故答案为:13或﹣11.
12.【解答】解:∵2×4x+1×16
=2×22x+2×24
=22x+7
=223,
∴2x+7=23,
∴x=8.
故答案为:8.
13.【解答】解:∵不透明盒子中装有6个白球和若干个其他颜色的球,这些球除颜色外完全相同,摸出一个球是白球的概率是,
∴白球占小球总数的,
∴这个盒子里一共有(个).
故答案为:15.
14.【解答】解:∵总面积为16个小正方形的面积,
如图所示,阴影部分的面积为4个由两个小正方形组成的长方形的一半,
∴阴影部分的面积为4个小正方形的面积,
∴小球停留在阴影区域的概率是,
故答案为:.
15.【解答】解:过点E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BEF=180°﹣∠ABE=60°,∠CEF=∠C=35°,
∴∠BEC=∠BEF+∠CEF=95°;
故答案为:95°.
16.【解答】解:设点P运动的时间为t秒,则BP=3t,CP=8﹣3t,
∵∠B=∠C,
∴①当BE=CP=6,BP=CQ时,△BPE与△CQP全等,
此时,6=8﹣3t,
解得t,
∴BP=CQ=2,
此时,点Q的运动速度为23厘米/秒;
②当BE=CQ=6,BP=CP时,△BPE与△CQP全等,
此时,3t=8﹣3t,
解得t,
∴点Q的运动速度为6厘米/秒;
故答案为:3或.
三、解答题
17.【解答】解:
=(4a2+4ab+b2﹣3a2+4ab﹣b2﹣a)÷(a)
=(a2+8ab﹣a)÷(a)
=﹣2a﹣16b+2,
当时,原式=﹣2×(﹣1)﹣162
=2﹣8+2
=﹣4.
18.【解答】解:原式=4+1﹣3
=5﹣3
=2.
19.【解答】解:(1)∵OD平分∠BOF,
∴,
∵∠COE+∠BOE+∠BOD=180°,
∴∠BOE=180°﹣110°﹣25°=45°;
(2)设∠AOC=x,∠AOF=7x,
∴∠AOC=∠BOD=x,
∵OD平分∠BOF,
∴,
∵∠AOC+∠AOF+∠FOD=180°,
∴x+7x+x=180°,
解得:x=20°,
∴∠BOD=∠FOD=20°,
∴∠BOF=20°×2=40°,
∵OB平分∠EOF,
∴∠EOB=∠BOF=40°,
∵∠COE+∠EOB+∠BOD=180°,
∴∠COE=180°﹣40°﹣20°=120°.
20.【解答】解:(1)阴影部分的面积=(3a+b)(2a+b)﹣(a+b)2
=6a2+5ab+b2﹣a2﹣2ab﹣b2
=5a2+3ab;
(2)当a=3,b=2时,原式=5×32+3×3×2=63(平方米).
21.【解答】解:(1)①这次抽取的学生总人数是9÷10%=90(人);
②C组人数为90﹣(9+12+24+21+9)=15(人),
则这些随机抽取的学生每日平均家务劳动时长约为(15×9+25×12+35×15+45×24+55×21+65×9)=42(min);
故答案为:90人;
(2)在本校学生中随机抽取一名学生,记事件A:该学生为“家务小能手”.
则事件A的概率约为.
22.【解答】(1)证明:在△ABC和△ADE中,
,
∴△ABC≌△ADE(SAS),
∴AC=AE.
(2)解:由(1)得△ABC≌△ADE,
∴∠BAC=∠DAE,
∵点C在线段AD上,
∴∠BAC=∠DAE,即∠BAC=∠CAE,
∵AC=AE,
∴∠ACE=∠AEC,
∵CE∥AB,
∴∠BAC=∠ACE,
∴∠CAE=∠ACE=∠AEC180°=60°,
∴∠BAC=∠CAE=60°,
∴∠BAC的度数是60°.
23.【解答】解:(1)方法1:根据题意可知,阴影部分面积为边长为a和边长为b的正方形面积之和,
∴;
方法2:根据题意可知,阴影部分面积为边长为(a+b)的正方形面积减去长为a,宽为b的长方形面积×2,
∴,
根据阴影部分面积相等可知:a2+b2=(a+b)2﹣2ab.
故答案为:a2+b2;(a+b)2﹣2ab;a2+b2=(a+b)2﹣2ab;
(2)∵a+b=6,a2+b2=20,
由(1)得:a2+b2=(a+b)2﹣2ab,
∴;
(3)设AC=x,BC=y,
∵AC+BC=8,S1+S2=25,
∴,
∴,
∴阴影部分的面积为.
24.【解答】解:(1)∵AB∥CD,
∴∠KEH=∠AFH,
∵∠AHE是△AHF的外角,
∴∠AHE=∠AFH+∠FAH,
∴∠AHE=∠FAH+∠KEH,
故答案为:∠AHE=∠FAH+∠KEH;
(2)∵AB∥CD,
∴∠BAK=∠MKE,∠ABE=∠BEC,
∵,
∴∠BAK=2∠BEF,
∵∠BEC=2∠BEF,
∴∠BAK=∠BEC,
∴∠BAK=∠ABE,
∵AK平分∠BAG,
∴∠BAK=∠ABE=∠GAK,
∵AG⊥BE,
∴∠AGB=90°,
∴3∠BAK=90°,
∴∠BAK=∠ABE=∠GAK=30°,
∴,
∴∠CEF=45°,
∴∠CEF=∠AFE=45°,
∴∠AHE=∠AFE+∠BAK=45°+30°=75°;
(3)①当KH∥NG时,延长KE交GN边于P,如图,
∵∠EKH=∠EPG=30°,
∴∠PEG=90°﹣∠EPG=60°,
∵∠GEN=90°﹣∠ENG=30°,
∴∠PEN=∠PEG﹣∠GEN=30°,
∴∠CEK=∠PEN=30°,
当△KHE绕E点旋转30°时,EK∥GN,
(秒);
②当KH∥EG时,如图,
∴∠EKH=∠KEG=30°,∠NEK=∠NEG+∠KEG=60°,
∴∠CEK=120°,
当△KHE绕点E旋转120°时,KH∥EG,
∴(秒);
③当KH∥EN时,即EK与EG在同一直线上时,
∴∠CEK=150°,
当△KHE绕点E旋转150°时,KH∥EN,
∴(秒);
④当KE∥NG时,
∵∠GEK=30°,
∴∠CEK=90°﹣∠GEK=60°,
当△KHE旋转60°时,KE∥NG,
∴(秒)
⑤当HE∥NG时,
∵∠GEK=30°,∠KEH=45°,
∴∠CEK=∠CEH+∠HEK=90°﹣∠GEK+∠HEK=105°,
∴当△KHE旋转105°时,HE∥NG,
∴(秒),
综上所述,当△KHE的其中一边与△ENG的某一边平行时,t的值为10,40,50,20,35.
25.【解答】(1)证明:过D作DM⊥BC.
∵BD为△ABC的角平分线,
∴DM=DA.
∵∠C=30°,
∴∠MDF+∠FDC=60°,
∵∠EDF=120°,
∴∠ADE+∠FDC=60°,
∴∠ADE=∠MDF.
在△AED和△MDF中,
,
∴△AED≌△MDF(AAS),
∴DE=DF.
(2)过F作FQ⊥GD,过D作DM⊥BC.
由(1)知△AED≌△MDF,
∴MF=AE,∠MDF=∠ADE,
∵∠EDF=∠EDM+∠MDF=120°,
∴∠EDM+∠ADE=120°,
∠ADM=120°,
∵∠A=∠DMB=90°,∠ABD=∠DBM,
∴∠ADB=∠BDM,
∵∠ADB+∠BDM=∠ADM=120°,
∴∠ADB=∠BDM=60°,
∵∠FDC=45°,∠EDF=120°,
∴∠ADE=15°,
∴∠EDG=60°﹣15°=45°.
∴∠GDF=120°﹣45°=75°.
∵∠EDF=120°,DE=DF,
∴∠DEG=∠DFG=30°,
∴∠FGD=75°,
∴∠FDG=∠FGD,
∴FG=FD,
∴GD=2QD.
在△FQD和△DMF中,
,
∴△FQD≌△DMF(AAS),
∴QD=MF,
∴DG=2AE.
(3)过E作EN⊥BDD,过F作FH⊥BD,过D作DM⊥BC,DR⊥EF.
由(2)∠AED=90°﹣∠ADE=75°,
∴∠BEG=180°﹣∠AED﹣∠DEG=75°,
又∠EGB=∠DGF=75°,
∴∠BEG=∠BGE,
∴BE=BG,
同理:FG=FD.
∴.
设BE=mx,BF=nx,
∵∠BEG=∠BGE=75°,
∴BG=BE=mx,
同理:BD=BF=nx,
∴GD=BD﹣BG=nx﹣mx=(n﹣m)x,
∴.
21世纪教育网(www.21cnjy.com)
同课章节目录
