2025年九年级数学中考三轮冲刺训练一次函数中几何压轴题综合训练(含答案)
文档属性
| 名称 | 2025年九年级数学中考三轮冲刺训练一次函数中几何压轴题综合训练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 19:25:40 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2025年九年级数学中考三轮冲刺训练一次函数中几何压轴题综合训练
1.在平面直角坐标系中,一次函数的图象l1与x轴、y轴分别交于点A、B,一次函数的图象l2与x轴、y轴分别交于点C、D.
(1)填空:点A的坐标为 ,点B的坐标为 ;
(2)在x轴上是否存在点P,使得2∠BPO+∠OBA=90°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)点Q为平面内一点,且△CDQ为等腰直角三角形,请直接写出所有满足条件的点Q的坐标.
2.如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)求k、b和m的值;
(2)求△ADC的面积;
(3)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.
3.如图,在平面直角坐标系中,直线y1=x+1与x轴、y轴分别交A、B两点,与直线相交于点C(3,m).
(1)求m和b的值;
(2)若直线与x轴相交于点D,动点P从点D开始,以每秒1个单位的速度向x轴负方向运动,设点P的运动时间为t秒.
①若点P在线段DA上,且△ACP的面积为10,求t的值;
②是否存在t的值,使△ACP为等腰三角形?若存在,求出t的值;若不存在,请说明理由.
4.如图,直线与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿M折叠,点B恰好落在x轴上的点B'处.求:
(1)求A、B两点坐标;
(2)求M坐标:
(3)在x轴上找一点P,使得以点P、M、B'为顶点的三角形是等腰三角形,请直接写出所有点P的坐标.
(4)在x轴上找一点N,且N点在A点的右侧,使得∠ABN=45°,请直接写出N点坐标.
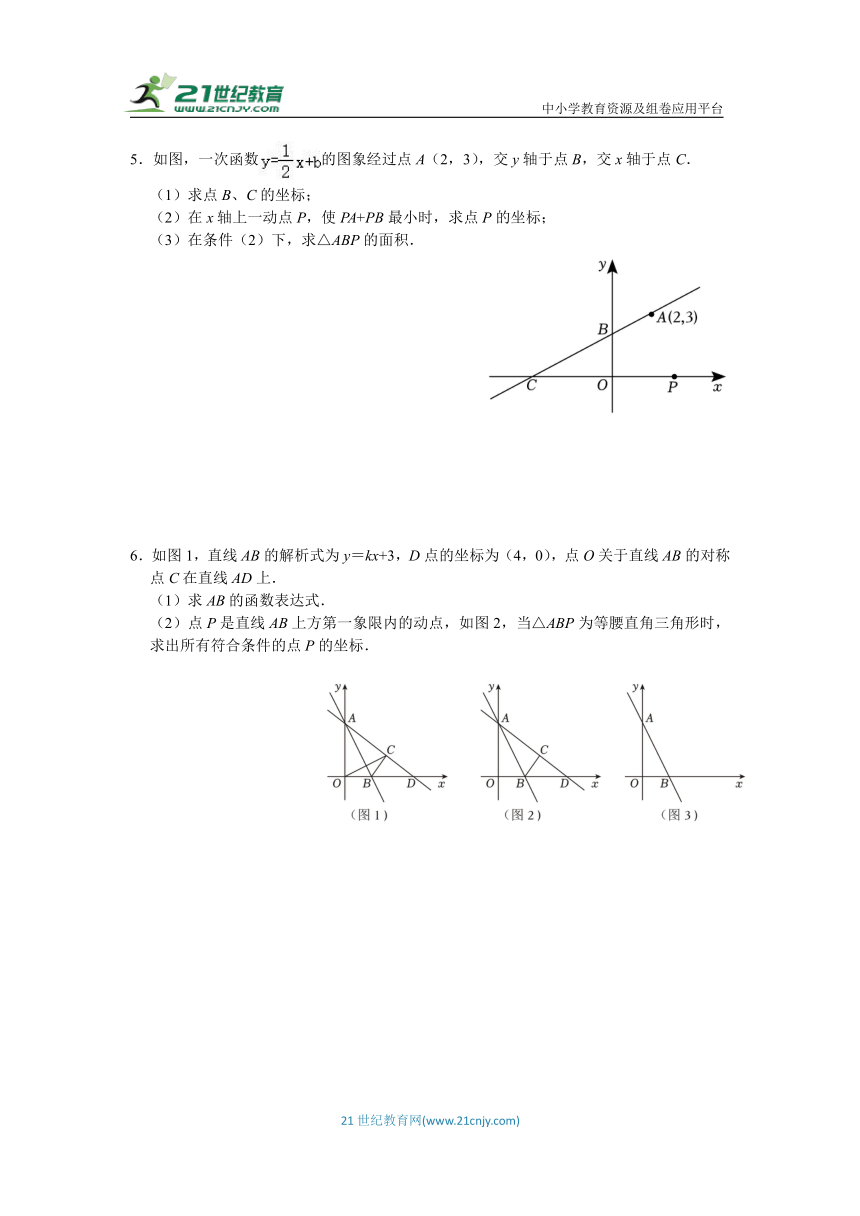
5.如图,一次函数的图象经过点A(2,3),交y轴于点B,交x轴于点C.
(1)求点B、C的坐标;
(2)在x轴上一动点P,使PA+PB最小时,求点P的坐标;
(3)在条件(2)下,求△ABP的面积.
6.如图1,直线AB的解析式为y=kx+3,D点的坐标为(4,0),点O关于直线AB的对称点C在直线AD上.
(1)求AB的函数表达式.
(2)点P是直线AB上方第一象限内的动点,如图2,当△ABP为等腰直角三角形时,求出所有符合条件的点P的坐标.
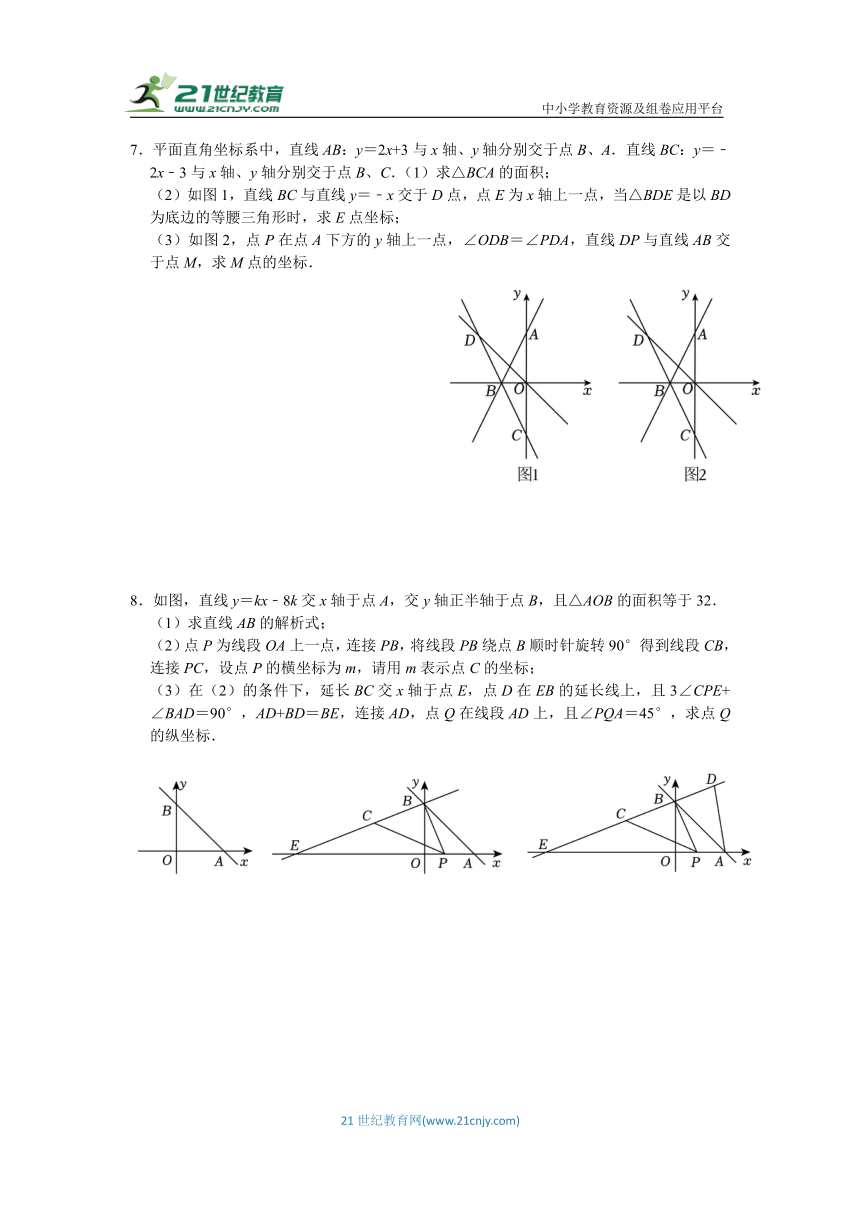
7.平面直角坐标系中,直线AB:y=2x+3与x轴、y轴分别交于点B、A.直线BC:y=﹣2x﹣3与x轴、y轴分别交于点B、C.(1)求△BCA的面积;
(2)如图1,直线BC与直线y=﹣x交于D点,点E为x轴上一点,当△BDE是以BD为底边的等腰三角形时,求E点坐标;
(3)如图2,点P在点A下方的y轴上一点,∠ODB=∠PDA,直线DP与直线AB交于点M,求M点的坐标.
8.如图,直线y=kx﹣8k交x轴于点A,交y轴正半轴于点B,且△AOB的面积等于32.
(1)求直线AB的解析式;
(2)点P为线段OA上一点,连接PB,将线段PB绕点B顺时针旋转90°得到线段CB,连接PC,设点P的横坐标为m,请用m表示点C的坐标;
(3)在(2)的条件下,延长BC交x轴于点E,点D在EB的延长线上,且3∠CPE+∠BAD=90°,AD+BD=BE,连接AD,点Q在线段AD上,且∠PQA=45°,求点Q的纵坐标.
9.在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=2x的图象平移得到,且经过点(﹣1,3),P(x,y)是一次函数图象上一点.
(1)求一次函数的解析式;
(2)求出一次函数y=kx+b(k≠0)的图象与x轴、y轴交点A和B的坐标;
(3)当△OAP的面积为5时,求点P的坐标.
10.如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足+|a+1|=0,点M为第三象限内的一点.
(1)直接写出A,B两点的坐标;
(2)若点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)若点M(2﹣m,2m﹣10)到坐标轴的距离相等,且MN∥AB,MN=AB,求点N的坐标.
11.如图1,已知直线l1:y=kx+b交x轴于A(6,0),交y轴于B(0,6).
(1)直接写出k的值为 ,b的值为 ;
(2)如图2,C为x轴负半轴上一点,过C点的直线经过AB的中点P,点Q(t,0)为x轴上一动点,过Q作QD⊥x轴分别交直线l1、l2于D、E,连接OD、OE、OQ得到△ODE和△ODQ,若其中一个三角形面积是另一个三角形面积的两倍,求c和t的值;
(3)如图3,已知点M(﹣2,0),点N(m,2m﹣6)为直线AB右侧一点,且满足∠OBM=∠ABN,求m的值.
12.在平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于点B,A.直线BC交y轴于点C(0,﹣4).
(1)求直线BC的解析式;
(2)如图2,直线BC与直线y=﹣x交于D点,点E为坐标轴上一点,当△BDE是以BD为底边的等腰三角形时,求OE的长;
(3)如图2,点P是A点下方y轴上的一点,且满足∠ODB=∠PDA,求点P坐标.
13.如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)在y轴右侧有一动直线平行于y轴,分别与l1,l2与交于点M、N,
①若线段MN=2,此时点N的坐标为 ;
②y轴上有一点Q,使△MNQ为等腰直角三角形,当点M在点N的下方时,请直接写出Q点的坐标.
14.如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0),B(0,4),点C在y轴的负半轴上,若将△CAB沿直线AC折叠,点B恰好落在x轴正半轴上的点D处.
(1)AB的长为 ,点D的坐标是 ;直线BE与直线CD的位置关系是 ;
(2)求点C的坐标;
(3)点M是y轴上一动点,若S△MAB=S△OCD,求出点M的坐标;
(4)在第一象限内是否存在点P,使△PAB为等腰直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.
15.如图,直线l:y=﹣2x+4与x轴、y轴分别交于点A、B,且与直线m相交于点M(1,2),已知直线m经过点C(﹣1,0),且与y轴交于点D.
(1)求点A、B的坐标以及直线m的解析式;
(2)若P为直线m上一动点,S△APM=2S△BDM,求点P的坐标;
(3)点Q是直线AB上方第一象限内的动点,当△ABQ为等腰直角三角形时,直接写出所有符合条件的点Q的坐标.
参考答案
1.【解答】解:(1)对于,当x=0时,y=﹣4,当y=0时,x=3,
∴点A的坐标为(3,0),点B的坐标为(0,﹣4);
故答案为(3,0);(0,﹣4);
(2)在x轴上存在点P,使得2∠BPO+∠OBA=90°,
∵点A的坐标为(3,0),点B的坐标为(0,﹣4),
∴OA=3,OB=4,
在Rt△OAB中,∠OAB+∠OBA=90°,
由勾股定理得:AB5,
∵2∠BPO+∠OBA=90°,
∴∠OAB=2∠BPO,
∴有以下两种情况:
①当点P在点A的右侧时,如图1所示:
∵∠OAB是△BAP的一个外角,
∴∠OAB=∠BPO+∠ABP,
∴2∠BPO=∠BPO+∠ABP,
∴∠BPO=∠ABP,
∴AP=AB=5,
∴OP=OA+AP=3﹣5=8,
∴点P的坐标为(8,0);
②当点P在点A的左侧时,作点A关于y轴的对称点E,连接BE,如图2所示:
∵OE=OA=3,BE=AB=5,∠OEB=∠OAB=2∠BPO,
∵∠OEB是△BPE的一个外角,
∴∠OEB=∠BPO+∠EBP=2∠BPO,
∴∠BPO=∠EBP,
∴PE=BE=5,
∴OP=OE+PE=3+5=8,
∴点P的坐标为(﹣8,0),
综上所述:点P的坐标为(8,0)或(﹣8,0);
(3)对于,当x=0时,y=2,当y=0时,x=﹣12,
∴点C的坐标为(﹣12,0),点D的坐标为(0,5),
∴OC=12,OD=5,
当△CDQ为等腰直角三角形时,有以下6中情况:
①当以点D为直角顶点,CD为腰,点Q在CD的上方时,过点Q作QF⊥y轴于点F,如图3所示:
∴∠COQ=90°,CD=DQ,∠COD=∠DFQ=90°,
∴∠CDO+∠QDF=90°,∠OCD+∠CDO=90°,
∴∠OCD=∠QDF,
在△OCD和△QDF中,
,
∴△OCD≌△QDF(AAS),
∴OD=QF=5,OC=DF=12,
∴OF=OD+DF=5+12=17,
∴点Q的坐标为(﹣5,17);
②当以点D为直角顶点,CD为腰,点Q在CD的下方时,过点Q作QFH⊥y轴于点H,如图4所示:
同理可证明:△OCD≌△HDQ(AAS),
∴OD=HQ=5,OC=DH=12,
∴OH=DH﹣OD=12﹣5=7,
∴点Q的坐标为(5,﹣7);
③当以点C为直角顶点,CD为腰,点Q在CD的上方时,过点Q作QG⊥x轴于点G,如图5所示:
同理可证明:△OCD≌△GQC(AAS),
∴OC=QG=12,OD=CG=5,
∴OD=OC+CG=12+5=17,
∴点Q的坐标为(﹣17,12);
④当以点C为直角顶点,CD为腰,点Q在CD的下方时,过点Q作QK⊥x轴于点K,如图6所示:
同理可证明:△OCD≌△KQC(AAS),
∴OD=CK=5,OC=KQ=12,
∴OK=OC﹣CK=12﹣5=7,
∴点Q的坐标为(﹣7,﹣12);
⑤当以CD为斜边,∠CQD=90°,且点Q在CD的上方时,过点Q作QT⊥x轴于点T,QR⊥y轴于点R,如图7所示:
∴∠QTO=∠QRO=∠TOR=90°,
∴四边形QTOR是矩形,
同理可证明:△QCT≌△QDR(AAS),
∴设CT=DR=a,QT=QR,
∴矩形QTOR是正方形,
∴OT=OR=a,
∵OT=OC﹣CT=12﹣a,OR=OD+DR=5+a,
∴12﹣a=5+a,
解得:a=3.5,
∴OT=12﹣a=8.5,
∴点Q的坐标为(﹣8.5,8.5);
⑥当以CD为斜边,∠CQD=90°,且点Q在CD的下方时,过点Q作OM⊥x轴于点M,QN⊥y轴于点N,如图8所示:
∴四边形QMON为矩形,
同理可证明:△QCM≌△QDN(AAS),
∴设QM=QN=a,CM=DN,
∴矩形QMON是正方形,
∴OM=ON=a,
∵CM=OC﹣OM=12﹣a,DN=OD+ON=5+a,
∴12﹣a=5+a,
解得:a=3.5,
∴QM=QN=3.5,
∴点Q的坐标为(﹣3.5,﹣3.5),
综上所述:所有满足条件的点Q的坐标为(﹣5,17)或(5,﹣7)或(﹣17,12)或(﹣7,﹣12)或(﹣8.5,8.5)或(﹣3.5,﹣3.5).
2.【解答】解:(1)∵直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),
∴5=1+b,
∴b=4,
∴直线l2:y=﹣x+4,
∵直线l2:y=﹣x+4经过点C(2,m),
∴m=﹣2+4=2,
∴C(2,2),
把C(2,2)代入y=kx+1,得到k.
∴k,b=4,m=2;
(2)对于直线l1:yx+1,令y=0,得到x=﹣2,
∴D(﹣2,0),
∴OD=2,
对于直线l2:y=﹣x+4,令y=0,得到x=4,
∴A(4,0),
∴OA=4,AD=6,
∵C(2,2),
∴S△ADC6×2=6;
(3)作点C关于x轴的对称点C′,连接BC′交x轴于E,连接EC,则△BCE的周长最小.
∵B(﹣1,5),C(2,2)关于x轴的对称点是(2,﹣2),
则设经过(2,﹣2)和B(﹣1,5)的函数解析式是y=mx+n,
则,
解得:,
则直线的解析式是yx.
令y=0,则x0,解得:x.
则E的坐标是(,0).
∴存在一点E,使△BCE的周长最短,E(,0).
3.【解答】解:(1)在平面直角坐标系中,直线y1=x+1与x轴、y轴分别交A、B两点,与直线相交于点C(3,m).将点C代入y=x+1得:
m=3+1=4,
将点C(3,4)代入直线得:
∴,
解得:b=5;
(2)在中,当y=0时,x=15,
D(15,0),
OD=15,
A(﹣1,0),
OA=1,
AD=1+15=16;
①设PD=t,则AP=16﹣t,过C作CE⊥AP于E,如图1所示:
则CE=4,
∵△ACP的面积为10,
∴,
解得:t=11;
②存在t的值,使△ACP为等腰三角形;理由如下:
过C作CE⊥AP于E,如图1所示:
则CE=4,OE=3,
∴AE=OA+OE=4,
∴;
a.当AC=PC时,AP=2AE=8,
PD=AD﹣AP=8,
t=8;
b.当AP=AC时,如图2所示:
则,
,,
或;
c.当PC=PA时,如图3所示:
设EP=m,则,AP=m+4,
∴,
解得:m=0,
∴P与E重合,AP=4,
PD=12,
t=12;
4.【解答】解:(1)直线与x轴、y轴分别交于点A和点B,
∴令y=0,则x=6;令x=0,则y=8,
∴A(6,0),B(0,8).
(2)∵A(6,0),B(0,8),
∴OA=6,OB=8,
∴,
由折叠的性质可知AB=AB′=10,BM=B′M
∴OB′=AB′﹣OA=4,
设OM=m,则B′M=BM=8﹣m,
在Rt△OB′M中,根据勾股定理得:m2+42=(8﹣m)2,解得:m=3,
∴M(0,3).
(3)点P的坐标为(4,0)或(﹣9,0)或(1,0)或;理由如下:
由(2)知OB′=4,OM=3,可得,
分以下几种情况讨论:
①如图1,以点M为圆心,B′M长为半径画圆交x轴于一点P,此时MP=MB′=5,
∴,
∴P(4,0);
②如图2,以点B′为圆心,B′M长为半径画圆交x轴于一点P,此时MP=MB′=5,
∴OP=9或1,
∴P(﹣9,0)或(1,0);
③如图3,作线段B′M的垂直平分线交x轴于一点P,此时MP=PB′,
设OP=x,则MP=B′P=4﹣x,
根据勾股定理得32+x2=(4﹣x)2,
解得:,
∴.
综合上述,点P的坐标为(4,0)或(﹣9,0)或(1,0)或.
(4)N(56,0);理由如下:
如图4:作∠ABN=45°,作AK⊥BN垂足为K,
∴∠KAB=∠ABN=45°,
∴BK=AK,
∵AB=10,AB2=BK2+AK2,
∴102=2AK2,
解得:,
∴,
设AN=x,则,
∴,
∵ON=6+x,
∴BN2=OB2+ON2,
∴,
解得:x=50或(不合题意,舍去),
∴ON=6+50=56,
∴N(56,0).
5.【解答】解:(1)将点A(2,3)代入一次函数,
得1+b=3,
∴b=2,
∴y=x+2,
当x=0时,y=2,
∴点B坐标为(0,2),
当y=x+2=0时,x=﹣4,
∴点C坐标为(﹣4,0);
(2)作点B关于x轴的对称点D,连接AD,交x轴于点P′,当点P与点P′重合时,
此时PA+PB最小,
∵点B坐标为(0,2),
∴点D坐标为(0,﹣2),
设直线AD的解析式为y=mx+n(m≠0,m,n为常数),
代入A(2,3),D(0,﹣2),
得,
解得,
∴直线AD的解析式为,
当=0时,x=,
∴点P′坐标为(,0),
∴PA+PB最小时,点P坐标为(,0);
(3)∵点C坐标为(﹣4,0),
∴CP==,
∴S△ABP=S△ACP﹣S△BCP
=
=.
6.【解答】解:(1)直线AB的解析式为y=kx+3,D点的坐标为(4,0),把x=0代入y=kx+3,得:y=3,
∴点A的坐标为(0,3),
∴OA=3,OD=4,
∵∠AOD=90°,
在直角三角形OAD中,由勾股定理得:,
∵点O关于直线AB的对称点C在直线AD上,
∴OA=AC=3,OB=BC,
∴CD=AD﹣AC=2,
设OB=BC=a,则BD=4﹣a,
在Rt△BCD中,由勾股定理得:BD2=BC2+CD2,
∴(4﹣a)2=a2+22,
解得,
∴点B的坐标为,
把代入y=kx+3,得:
,
解得k=﹣2,
∴直线AB的解析式为y=﹣2x+3;
(2)点P是直线AB上方第一象限内的动点,当△ABP为等腰直角三角形时,分以下三种情况讨论:
①若∠PAB=90°,AP=AB,过点P作PM⊥y轴,垂足为M,如图1,
∵∠MAP+∠APM=90°,∠MAP+∠BAO=90°,
∴∠APM=∠BAO,
∵∠PMA=∠AOB=90°,PA=AB,
∴△APM≌△BAO(AAS),
∴,
∴,
∴点P的坐标为;
②若∠ABP=90°,BA=BP,如图2,过点P作PM⊥x轴,垂足为M,
∵∠ABO+∠BAO=90°,∠ABO+∠PBM=90°,
∴∠BAO=∠PBM,
∵∠AOB=∠BMP=90°,BA=BP,
∴△AOB≌△BMP(AAS),
∴,
∴,
∴点P的坐标为;
③若∠APB=90°,PA=PB,如图3,过点P作直线垂直x轴,交x轴于N,过点A作AM⊥PN,垂足为M,
设点P的坐标为(m,n),
∵∠APM+∠PAM=90°,∠APM+∠BPN=90°,
∴∠PAM=∠BPN,
∵∠AMP=∠PNB=90°,PA=PB,
∴△APM≌△PBN(AAS),
∴AM=PN,PM=BN,
即,
解得,
∴点P的坐标为;
综上所述,点P的坐标为或或.
7.【解答】解:(1)在y=2x+3中,当x=0时,y=3,
在y=﹣2x﹣3中,当x=0时,y=﹣3,当y=0时,,
∴,
∴,
∴;
(2)联立,
解得,
∴D点的坐标是(﹣3,3),
设点E的坐标为(t,0),则,DE2=(﹣3﹣t)2+(3﹣0)2,
∵△BDE是以BD为底边的等腰三角形,
∴BE=DE,
∴BE2=DE2,
∴,
∴,
解得,
∴;
(3)如图,当点P在点A的下方,
∵A(0,3),D(﹣3,3),
∴AD=OA,AD⊥y轴,
∴∠ADO=∠ADP+∠PDO=45°,
∵∠ODB=∠PDA,
∴∠PDB=∠ODB+∠PDO=45°;
过点B作BN⊥BD交直线DP于点N,过点N作NQ⊥OB于点Q,过点D作DH⊥OB于点H,
∴△DBN为等腰直角三角形,
∴DB=BN,
∵∠BDH+∠DBH=90°,∠DBH+∠NBQ=90°,
∴∠BDH=∠NBQ,
在△DHB和△BQN中,
,
∴△DHB≌△BQN(AAS),
∴,BQ=DH=3,
∴,
∴,
设直线DN的解析式为y=kx+b,
∴,
解得:,
∴直线DN的解析式为,
联立直线AB和DN解析式得到,
解得:即,.
8.【解答】解:(1)∵直线y=kx﹣8k交x轴于点A,交y轴正半轴于点B,
∴点A(8,0),B(0,﹣8k),
∴OA=8,OB=﹣8k,
∵△AOB的面积等于32,
∴S△AOB=,
∴k=﹣1,
∴直线AB的解析式为y=﹣x+8;
(2)∵把线段PB绕点B顺时针旋转90°得到线段CB,
∴PB=BC,∠PBC=90°,
∴∠CBE+∠PBE=90°,
如图,过点C作CE⊥y轴于点E,
则∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠BCE=∠PBE,
在△CEB和△BOP中,
,
∴△CEB≌△BOP(AAS),
∴CE=BO=8,BE=OP=m,
∴OE=OB﹣BE=8﹣m,
∴C(﹣8,8﹣m);
(3)如图,延长BD至N,使DN=AD,过点N作NK⊥x轴于K,连接AN,
∵BC=BP,∠CBP=90°,
∴∠BCP=∠BPC=45°,
同理∠BAO=45°,
设∠CPE=α,则∠E=∠BCP﹣CPE=45°﹣α,
∵3∠CPE+∠BAD=90°,
∴∠BAD=90°﹣3α,
∵∠DBA=∠E+∠BAO,
∴∠DBA=90°﹣α,
∴∠ADB=180°﹣∠DBA﹣∠BAD=4α,
∵DN=AD,
∴∠DNA=∠DAN=2α,
∴∠NAB=∠DAN+∠BAD=90°﹣3α+2α=90°﹣α,
∴∠DBA=∠NAB,
∴NB=NA,
∵AD+BD=BE,
∴DN+BD=BE=BN
∴NA=BE,
在Rt△ENK中,∠ENK=90°﹣∠E=45°+α,
∴∠ANK=∠ENK﹣∠ANB=45°+α﹣2α=45°﹣α,
∴∠ANK=∠E,
∵∠EOB=∠NKA=90°,
在△EOB和△NKA中,
,
∴△EOB≌△NKA(AAS),
∴AK=OB=8,EO=NK,
∴△EOB∽△EKN,
∴,
∴EO=NK=16,
∴E(﹣16,0),N(16,16),
设直线EB表达式为y=kx+b,
则,
解得,
∴直线EB表达式为,
设,
∵DA=DN,
∴,
解得d=6,
∴D(6,11),
如图,过点D作DR⊥x轴于点R,Q作QS⊥x轴于点S,过点P作PT⊥AD于点T,
则DR=11,AR=8﹣6=2,
由勾股定理得,
∴,,,
而∠BPO=45°+α,则∠OBP=∠E=45°﹣α,
∴,
∴OP=4,则AP=4,
∴,,
∵∠PQA=45°,
∴,
∴,
∴,,
∴,
∴.
9.【解答】解:(1)因为一次函数y=kx+b(k≠0)的图象由函数y=2x的图象平移得到,
所以k=2.
将点(﹣1,3)的坐标代入y=2x+b得,
﹣2+b=3,
解得b=5,
所以一次函数的解析式为y=2x+5.
(2)将x=0代入y=2x+5得,
y=5,
所以点B的坐标为(0,5).
将y=0代入y=2x+5得,
x=,
所以点A的坐标为().
(3)因为△OAP的面积为5,
所以,
解得y=±4.
当y=4时,
2x+5=4,
解得x=,
所以点P的坐标为().
当y=﹣4时,
2x+5=﹣4,
解得x=,
所以点P的坐标为(),
综上所述,点P的坐标为()或().
10.【解答】解:(1)∵+|a+1|=0,
∴=0,|a+1|=0,
∴b﹣3=0,a+1=0,
∴a=﹣1,b=3,
∴A(﹣1,0),B(3,0).
(2)∵点M为第三象限内的一点,
∴m<0,
∵AB=|﹣1﹣3|=4,
∴△ABM的面积为AB (﹣m)=﹣2m.
(3)∵点M为第三象限内的一点,且点M(2﹣m,2m﹣10)到坐标轴的距离相等,
∴2﹣m=2m﹣10,
∴m=4,
∴M(﹣2,﹣2),
∵MN∥AB,AB=4,
∴﹣2﹣4=﹣6,﹣2+4=2,
∴点N的坐标是(2,﹣2)或(﹣6,﹣2).
11.【解答】解:(1)把A(6,0),B(0,6)代入y=kx+b得:
,
解得,
故答案为:﹣1,6;
(2)如图:
∵A(6,0),B(0,6),
∴线段AB的中点P的坐标为(3,3),
把P(3,3)代入y=x+c得:3=+c,
解得c=,
∴直线l2的解析式为y=x+,
由(1)知直线l1的解析式为y=﹣x+6,
∵Q(t,0),QD⊥x轴,
∴D(t,﹣t+6),E(t,t+),
∴DE=|﹣t+6﹣(t+)|=|﹣t+|,DQ=|﹣t+6|,
∵△ODE和△ODQ,其中一个三角形面积是另一个三角形面积的两倍,
∴DE=2DQ或DQ=2DE,
∴|﹣t+|=2|﹣t+6|或|﹣t+6|=2|﹣t+|,
∴﹣t+=2(﹣t+6)或﹣t+=﹣2(﹣t+6)或﹣t+6=2(﹣t+)或﹣t+6=﹣2(﹣t+),
解得t=15或t=或t=或t=;
(3)作M关于y轴的对称点G(2,0),以G为直角顶点,BG为直角边在BG右侧作等腰直角三角形BGH,过H作HK⊥x轴于K,如图:
∴∠OBM=∠OBG,
∵A(6,0),B(0,6),
∴△AOB是等腰直角三角形,
∴∠OBG+∠ABG=45°,
∵△BGH是等腰直角三角形,
∴∠ABG+∠ABH=45°,BG=GH,
∴∠OBG=∠ABH,
∴∠OBM=∠ABH,
∴N在直线BH上,
∵∠OGB=90°﹣∠HGK=∠GHK,∠BOG=∠GKH=90°,BG=GH,
∴△BOG≌△GKH(AAS),
∴BO=GK=6,OG=HK=2,
∴H(8,2),
由B(0,6),H(8,2)可得直线BH解析式为y=﹣x+6,
把N(m,2m﹣6)代入得:
2m﹣6=﹣m+6,
解得m=.
12.【解答】解:(1)在y=2x+4中,令x=0,y=4,令y=0,x=﹣2,
∴B(﹣2,0),
设直线BC的解析式为y=kx+b,
∴,
∴,
∴直线BC的解析式为y=﹣2x﹣4;
(2)联立,
解得,
∴D点的坐标是(﹣4,4),
设点E的坐标为(t,0),则BE2=(﹣2﹣t)2,DE2=(﹣4﹣t)2+(4﹣0)2,
∵△BDE是以BD为底边的等腰三角形,
∴BE=DE,
∴BE2=DE2,
∴(﹣2﹣t)2=(﹣4﹣t)2+(4﹣0)2,
解得t=﹣,
∴E(﹣,0),
∴OE=;
设E(0,t),则BE2=4+t2,DE2=(﹣4﹣0)2+(4﹣t)2,
∵△BDE是以BD为底边的等腰三角形,
∴BE=DE,
∴BE2=DE2,
∴4+t2=(﹣4﹣0)2+(4﹣t)2,
解得t=,
∴E(0,),
∴OE=;
(3)如图,当点P在点A的下方,
∵A(0,4),D(﹣4,4),
∴AD=OA,AD⊥y轴,
∴∠ADO=∠ADP+∠PDO=45°,
∵∠ODB=∠PDA,
∴∠PDB=∠ODB+∠PDO=45°;
过点B作BN⊥BD交直线DP于点N,过点N作NQ⊥OB于点Q,过点D作DH⊥OB于点H,
∴△DBN为等腰直角三角形,
∴DB=BN,
∵∠BDH+∠DBH=90°,∠DBH+∠NBQ=90°,
∴∠BDH=∠NBQ,
在△DHB和△BQN中,
,
∴△DHB≌△BQN(AAS),
∴NQ=BH=﹣2﹣(﹣4)=2,BQ=DH=4,
∴OQ=BQ﹣BO=2,
∴N(2,2),
设直线DN的解析式为y=kx+b,
∴,
解得,
∴直线DN的解析式为y=﹣x+,
当x=0时,y=,
∴P(0,).
13.【解答】解:(1)∵直线l2:与x轴、y轴分别交于点A、点B,
故把x=0,则y=3;
把y=0,则x=6,
∴与x轴、y轴分别交于点A、点B坐标分别为(6,0)、(0,3),
∵直线l1与l2交于点C,
联立得方程组:两个函数表达式得:﹣x+3=x,
解得:x=2,
故点C(2,2);
则△COB的面积=OB×xC==3;
(2)①设点M、N的坐标分别为(m,m)、(m,3﹣m),
根据题意可得:|m﹣(3﹣m)|=2,
解得:m=或m=,
所以点N的坐标为: 或,
故答案为: 或;
②y轴上存在点Q,使△MNQ为等腰直角三角形,理由如下:
设M、N、Q的坐标分别为(m,m)、(m,3﹣m)、(0,n),
当∠MQN=90°时,
如图1.2,作PQ⊥MN交MN于点P,
由题意得:MN=2PQ,
∴﹣m+3﹣m=2m,
解得:m=,
∴Q点坐标为:(0,);
当∠QNM=90°时,如图2:
则MN=QN,即:3﹣m﹣m=m,
解得:m=,
∴Q点坐标为:(0,);
当∠NMQ=90°时,如图3:
则MN=QM,即:3﹣m﹣m=m,
解得:m=,
∴Q点坐标为:(0,),
综上,点Q的坐标为:.
14.【解答】解:(1)在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0),B(0,4),
∴OA=3,OB=4,
在Rt△AOB中,由勾股定理得:AB==5,
由折叠的性质可知,AD=AB=5,
∴OD=OA+AD=3+5=8,
∴点D的坐标是(8,0),
设OC=x,则BC=OB+OC=4+x,
由折叠的性质可知,CD=BC=4+x,
在Rt△COD中,由勾股定理得:OC2+OD2=CD2,
∴x2+82=(x+4)2,
解得:x=6,即OC=6,
∴点C的坐标为(0,﹣6);
由C、D的坐标得,直线CD的表达式为:y=x﹣8,
同理可得:直线AB的表达式为:y=x+4,
故直线BE与直线CD的位置关系是垂直,
故答案为:5,(8,0),垂直;
(2)由(1)得,点C的坐标为(0,﹣6);
(3)∵C(0,﹣6),D(8,0),
∴OC=6,OD=8,
则S△COD===24,
则S△MAB=12,
∵点M是y轴上一动点,
∴设点M的坐标为(0,m),
∴BM=|m﹣4|,
则S△MAB=BM OA=|m﹣4|×3=12,
∴m=12或﹣4,
∴点M的坐标为(0,12)或(0,﹣4);
(4)在第一象限内存在点P,使△PAB为等腰直角三角形;理由如下:
①当∠BAP=90°,AB=AP,则△PAB为等腰直角三角形,
如图1,过点P作PG⊥x轴于点G,
∴∠PGA=∠AOB=90°,
∵∠BAP=90°,
∴∠BAO+∠PAG=90°,
∵∠ABO+∠BAO=90°,
∴∠ABO=∠PAG,
在△AOB和△PGA中,∠ABO=∠PAG,∠AOB=∠PGA,AB=PA,
∴△AOB≌△PGA(AAS),
∴OA=PG=3,OB=AG=4,
∴OG=OA+AG=7,
∴点P的坐标为(7,3);
②当∠ABP=90°,BA=BP,则△PAB为等腰直角三角形,
如图2,过点P作PH⊥y轴于点H,
同理 可证,△AOB≌△BHP(AAS),
∴OA=BH=3,PH=OB=4,
∴OH=OB+BH=7,
∴点P的坐标为(4,7);
③当∠APB=90°,PA=PB,则△PAB为等腰直角三角形,
如图3,过点P作PM⊥x轴于点M,PN⊥y轴于点N,
∴∠PNB=∠PMA=∠MPN=90°,
∴∠APN+∠APM=90°,
∵∠APB=90°,
∴∠BPN+∠APN=90°,
∴∠APM=∠BPN,
在△APM和△BPN中,∠APM=∠BPN,PA=PB,∠PMA=∠PNB,
∴△APM≌△BPN(ASA),
∴AM=BN,PM=PN,
∴设点P的坐标为(p,p),
∴OM=ON=p,
∴BN=OB﹣ON=4﹣p,AM=OM﹣OA=p﹣3,
∴4﹣p=p﹣3,
解得:p=,
则点P的坐标为(,),
综上可知,第一象限内存在点P,使△PAB为等腰直角三角形,点P的坐标(7,3)或(4,7)或(,).
15.【解答】解:(1)在y=﹣2x+4中,令x=0得y=4,令y=0得x=2,
∴A(2,0),B(0,4),
设直线m的解析式为y=kx+b,把M(1,2),C(﹣1,0)代入得:
,
解得,
∴直线m的解析式为y=x+1;
(2)在y=x+1中,令x=0得y=1,令y=0得x=﹣1,
∴C(﹣1,0),D(0,1),
∵B(0,4),
∴BD=3,
∵M(1,2),
∴S△BDM=×3×1=,
∵S△APM=2S△BDM,
∴S△APM=3;
∵A(2,0),C(﹣1,0),
∴AC=3,
∵M(1,2),
∴S△ACM=×3×2=3;
①当P与C重合时,S△APM=S△ACM=3=2S△BDM,此时P(﹣1,0);
②当P在AB右侧时,S△APC=S△APM+S△ACM=3+3=6,
∴×3 yP=6,
∴yP=4,
在y=x+1中,令y=4得x=3,
∴P(3,4);
综上所述,P的坐标为(﹣1,0)或(3,4);
(3)设Q(p,q),
∵A(2,0),B(0,4),
∴QA2=(p﹣2)2+q2,QB2=p2+(q﹣4)2,AB2=20,
①当QA为等腰直角三角形斜边时,QA2=2AB2,QB2=AB2,
∴,
解得(此时Q不在第一象限,舍去)或,
∴Q(4,6);
②当QB为等腰直角三角形斜边时,QB2=2AB2,QA2=AB2,
∴,
解得或(舍去),
∴Q(6,2);
③当AB为等腰直角三角形斜边时,QA2=AB2,QA2=QB2,
∴,
解得(舍去)或,
∴Q(3,3);
综上所述,Q的坐标为(4,6)或(6,2)或(3,3).
21世纪教育网(www.21cnjy.com)
2025年九年级数学中考三轮冲刺训练一次函数中几何压轴题综合训练
1.在平面直角坐标系中,一次函数的图象l1与x轴、y轴分别交于点A、B,一次函数的图象l2与x轴、y轴分别交于点C、D.
(1)填空:点A的坐标为 ,点B的坐标为 ;
(2)在x轴上是否存在点P,使得2∠BPO+∠OBA=90°?若存在,求出点P的坐标;若不存在,请说明理由;
(3)点Q为平面内一点,且△CDQ为等腰直角三角形,请直接写出所有满足条件的点Q的坐标.
2.如图,直线l1:y=kx+1与x轴交于点D,直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),直线l1与l2交于点C(2,m).
(1)求k、b和m的值;
(2)求△ADC的面积;
(3)在x轴上是否存在一点E,使△BCE的周长最短?若存在,请求出点E的坐标;若不存在,请说明理由.
3.如图,在平面直角坐标系中,直线y1=x+1与x轴、y轴分别交A、B两点,与直线相交于点C(3,m).
(1)求m和b的值;
(2)若直线与x轴相交于点D,动点P从点D开始,以每秒1个单位的速度向x轴负方向运动,设点P的运动时间为t秒.
①若点P在线段DA上,且△ACP的面积为10,求t的值;
②是否存在t的值,使△ACP为等腰三角形?若存在,求出t的值;若不存在,请说明理由.
4.如图,直线与x轴、y轴分别交于点A和点B,M是OB上的一点,若将△ABM沿M折叠,点B恰好落在x轴上的点B'处.求:
(1)求A、B两点坐标;
(2)求M坐标:
(3)在x轴上找一点P,使得以点P、M、B'为顶点的三角形是等腰三角形,请直接写出所有点P的坐标.
(4)在x轴上找一点N,且N点在A点的右侧,使得∠ABN=45°,请直接写出N点坐标.
5.如图,一次函数的图象经过点A(2,3),交y轴于点B,交x轴于点C.
(1)求点B、C的坐标;
(2)在x轴上一动点P,使PA+PB最小时,求点P的坐标;
(3)在条件(2)下,求△ABP的面积.
6.如图1,直线AB的解析式为y=kx+3,D点的坐标为(4,0),点O关于直线AB的对称点C在直线AD上.
(1)求AB的函数表达式.
(2)点P是直线AB上方第一象限内的动点,如图2,当△ABP为等腰直角三角形时,求出所有符合条件的点P的坐标.
7.平面直角坐标系中,直线AB:y=2x+3与x轴、y轴分别交于点B、A.直线BC:y=﹣2x﹣3与x轴、y轴分别交于点B、C.(1)求△BCA的面积;
(2)如图1,直线BC与直线y=﹣x交于D点,点E为x轴上一点,当△BDE是以BD为底边的等腰三角形时,求E点坐标;
(3)如图2,点P在点A下方的y轴上一点,∠ODB=∠PDA,直线DP与直线AB交于点M,求M点的坐标.
8.如图,直线y=kx﹣8k交x轴于点A,交y轴正半轴于点B,且△AOB的面积等于32.
(1)求直线AB的解析式;
(2)点P为线段OA上一点,连接PB,将线段PB绕点B顺时针旋转90°得到线段CB,连接PC,设点P的横坐标为m,请用m表示点C的坐标;
(3)在(2)的条件下,延长BC交x轴于点E,点D在EB的延长线上,且3∠CPE+∠BAD=90°,AD+BD=BE,连接AD,点Q在线段AD上,且∠PQA=45°,求点Q的纵坐标.
9.在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=2x的图象平移得到,且经过点(﹣1,3),P(x,y)是一次函数图象上一点.
(1)求一次函数的解析式;
(2)求出一次函数y=kx+b(k≠0)的图象与x轴、y轴交点A和B的坐标;
(3)当△OAP的面积为5时,求点P的坐标.
10.如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足+|a+1|=0,点M为第三象限内的一点.
(1)直接写出A,B两点的坐标;
(2)若点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)若点M(2﹣m,2m﹣10)到坐标轴的距离相等,且MN∥AB,MN=AB,求点N的坐标.
11.如图1,已知直线l1:y=kx+b交x轴于A(6,0),交y轴于B(0,6).
(1)直接写出k的值为 ,b的值为 ;
(2)如图2,C为x轴负半轴上一点,过C点的直线经过AB的中点P,点Q(t,0)为x轴上一动点,过Q作QD⊥x轴分别交直线l1、l2于D、E,连接OD、OE、OQ得到△ODE和△ODQ,若其中一个三角形面积是另一个三角形面积的两倍,求c和t的值;
(3)如图3,已知点M(﹣2,0),点N(m,2m﹣6)为直线AB右侧一点,且满足∠OBM=∠ABN,求m的值.
12.在平面直角坐标系中,直线y=2x+4与x轴、y轴分别交于点B,A.直线BC交y轴于点C(0,﹣4).
(1)求直线BC的解析式;
(2)如图2,直线BC与直线y=﹣x交于D点,点E为坐标轴上一点,当△BDE是以BD为底边的等腰三角形时,求OE的长;
(3)如图2,点P是A点下方y轴上的一点,且满足∠ODB=∠PDA,求点P坐标.
13.如图,在平面直角坐标系中,直线l1的解析式为y=x,直线l2的解析式为,与x轴、y轴分别交于点A、点B,直线l1与l2交于点C.
(1)求点A、点B、点C的坐标,并求出△COB的面积;
(2)在y轴右侧有一动直线平行于y轴,分别与l1,l2与交于点M、N,
①若线段MN=2,此时点N的坐标为 ;
②y轴上有一点Q,使△MNQ为等腰直角三角形,当点M在点N的下方时,请直接写出Q点的坐标.
14.如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0),B(0,4),点C在y轴的负半轴上,若将△CAB沿直线AC折叠,点B恰好落在x轴正半轴上的点D处.
(1)AB的长为 ,点D的坐标是 ;直线BE与直线CD的位置关系是 ;
(2)求点C的坐标;
(3)点M是y轴上一动点,若S△MAB=S△OCD,求出点M的坐标;
(4)在第一象限内是否存在点P,使△PAB为等腰直角三角形,若存在,直接写出点P的坐标;若不存在,请说明理由.
15.如图,直线l:y=﹣2x+4与x轴、y轴分别交于点A、B,且与直线m相交于点M(1,2),已知直线m经过点C(﹣1,0),且与y轴交于点D.
(1)求点A、B的坐标以及直线m的解析式;
(2)若P为直线m上一动点,S△APM=2S△BDM,求点P的坐标;
(3)点Q是直线AB上方第一象限内的动点,当△ABQ为等腰直角三角形时,直接写出所有符合条件的点Q的坐标.
参考答案
1.【解答】解:(1)对于,当x=0时,y=﹣4,当y=0时,x=3,
∴点A的坐标为(3,0),点B的坐标为(0,﹣4);
故答案为(3,0);(0,﹣4);
(2)在x轴上存在点P,使得2∠BPO+∠OBA=90°,
∵点A的坐标为(3,0),点B的坐标为(0,﹣4),
∴OA=3,OB=4,
在Rt△OAB中,∠OAB+∠OBA=90°,
由勾股定理得:AB5,
∵2∠BPO+∠OBA=90°,
∴∠OAB=2∠BPO,
∴有以下两种情况:
①当点P在点A的右侧时,如图1所示:
∵∠OAB是△BAP的一个外角,
∴∠OAB=∠BPO+∠ABP,
∴2∠BPO=∠BPO+∠ABP,
∴∠BPO=∠ABP,
∴AP=AB=5,
∴OP=OA+AP=3﹣5=8,
∴点P的坐标为(8,0);
②当点P在点A的左侧时,作点A关于y轴的对称点E,连接BE,如图2所示:
∵OE=OA=3,BE=AB=5,∠OEB=∠OAB=2∠BPO,
∵∠OEB是△BPE的一个外角,
∴∠OEB=∠BPO+∠EBP=2∠BPO,
∴∠BPO=∠EBP,
∴PE=BE=5,
∴OP=OE+PE=3+5=8,
∴点P的坐标为(﹣8,0),
综上所述:点P的坐标为(8,0)或(﹣8,0);
(3)对于,当x=0时,y=2,当y=0时,x=﹣12,
∴点C的坐标为(﹣12,0),点D的坐标为(0,5),
∴OC=12,OD=5,
当△CDQ为等腰直角三角形时,有以下6中情况:
①当以点D为直角顶点,CD为腰,点Q在CD的上方时,过点Q作QF⊥y轴于点F,如图3所示:
∴∠COQ=90°,CD=DQ,∠COD=∠DFQ=90°,
∴∠CDO+∠QDF=90°,∠OCD+∠CDO=90°,
∴∠OCD=∠QDF,
在△OCD和△QDF中,
,
∴△OCD≌△QDF(AAS),
∴OD=QF=5,OC=DF=12,
∴OF=OD+DF=5+12=17,
∴点Q的坐标为(﹣5,17);
②当以点D为直角顶点,CD为腰,点Q在CD的下方时,过点Q作QFH⊥y轴于点H,如图4所示:
同理可证明:△OCD≌△HDQ(AAS),
∴OD=HQ=5,OC=DH=12,
∴OH=DH﹣OD=12﹣5=7,
∴点Q的坐标为(5,﹣7);
③当以点C为直角顶点,CD为腰,点Q在CD的上方时,过点Q作QG⊥x轴于点G,如图5所示:
同理可证明:△OCD≌△GQC(AAS),
∴OC=QG=12,OD=CG=5,
∴OD=OC+CG=12+5=17,
∴点Q的坐标为(﹣17,12);
④当以点C为直角顶点,CD为腰,点Q在CD的下方时,过点Q作QK⊥x轴于点K,如图6所示:
同理可证明:△OCD≌△KQC(AAS),
∴OD=CK=5,OC=KQ=12,
∴OK=OC﹣CK=12﹣5=7,
∴点Q的坐标为(﹣7,﹣12);
⑤当以CD为斜边,∠CQD=90°,且点Q在CD的上方时,过点Q作QT⊥x轴于点T,QR⊥y轴于点R,如图7所示:
∴∠QTO=∠QRO=∠TOR=90°,
∴四边形QTOR是矩形,
同理可证明:△QCT≌△QDR(AAS),
∴设CT=DR=a,QT=QR,
∴矩形QTOR是正方形,
∴OT=OR=a,
∵OT=OC﹣CT=12﹣a,OR=OD+DR=5+a,
∴12﹣a=5+a,
解得:a=3.5,
∴OT=12﹣a=8.5,
∴点Q的坐标为(﹣8.5,8.5);
⑥当以CD为斜边,∠CQD=90°,且点Q在CD的下方时,过点Q作OM⊥x轴于点M,QN⊥y轴于点N,如图8所示:
∴四边形QMON为矩形,
同理可证明:△QCM≌△QDN(AAS),
∴设QM=QN=a,CM=DN,
∴矩形QMON是正方形,
∴OM=ON=a,
∵CM=OC﹣OM=12﹣a,DN=OD+ON=5+a,
∴12﹣a=5+a,
解得:a=3.5,
∴QM=QN=3.5,
∴点Q的坐标为(﹣3.5,﹣3.5),
综上所述:所有满足条件的点Q的坐标为(﹣5,17)或(5,﹣7)或(﹣17,12)或(﹣7,﹣12)或(﹣8.5,8.5)或(﹣3.5,﹣3.5).
2.【解答】解:(1)∵直线l2:y=﹣x+b与x轴交于点A,且经过定点B(﹣1,5),
∴5=1+b,
∴b=4,
∴直线l2:y=﹣x+4,
∵直线l2:y=﹣x+4经过点C(2,m),
∴m=﹣2+4=2,
∴C(2,2),
把C(2,2)代入y=kx+1,得到k.
∴k,b=4,m=2;
(2)对于直线l1:yx+1,令y=0,得到x=﹣2,
∴D(﹣2,0),
∴OD=2,
对于直线l2:y=﹣x+4,令y=0,得到x=4,
∴A(4,0),
∴OA=4,AD=6,
∵C(2,2),
∴S△ADC6×2=6;
(3)作点C关于x轴的对称点C′,连接BC′交x轴于E,连接EC,则△BCE的周长最小.
∵B(﹣1,5),C(2,2)关于x轴的对称点是(2,﹣2),
则设经过(2,﹣2)和B(﹣1,5)的函数解析式是y=mx+n,
则,
解得:,
则直线的解析式是yx.
令y=0,则x0,解得:x.
则E的坐标是(,0).
∴存在一点E,使△BCE的周长最短,E(,0).
3.【解答】解:(1)在平面直角坐标系中,直线y1=x+1与x轴、y轴分别交A、B两点,与直线相交于点C(3,m).将点C代入y=x+1得:
m=3+1=4,
将点C(3,4)代入直线得:
∴,
解得:b=5;
(2)在中,当y=0时,x=15,
D(15,0),
OD=15,
A(﹣1,0),
OA=1,
AD=1+15=16;
①设PD=t,则AP=16﹣t,过C作CE⊥AP于E,如图1所示:
则CE=4,
∵△ACP的面积为10,
∴,
解得:t=11;
②存在t的值,使△ACP为等腰三角形;理由如下:
过C作CE⊥AP于E,如图1所示:
则CE=4,OE=3,
∴AE=OA+OE=4,
∴;
a.当AC=PC时,AP=2AE=8,
PD=AD﹣AP=8,
t=8;
b.当AP=AC时,如图2所示:
则,
,,
或;
c.当PC=PA时,如图3所示:
设EP=m,则,AP=m+4,
∴,
解得:m=0,
∴P与E重合,AP=4,
PD=12,
t=12;
4.【解答】解:(1)直线与x轴、y轴分别交于点A和点B,
∴令y=0,则x=6;令x=0,则y=8,
∴A(6,0),B(0,8).
(2)∵A(6,0),B(0,8),
∴OA=6,OB=8,
∴,
由折叠的性质可知AB=AB′=10,BM=B′M
∴OB′=AB′﹣OA=4,
设OM=m,则B′M=BM=8﹣m,
在Rt△OB′M中,根据勾股定理得:m2+42=(8﹣m)2,解得:m=3,
∴M(0,3).
(3)点P的坐标为(4,0)或(﹣9,0)或(1,0)或;理由如下:
由(2)知OB′=4,OM=3,可得,
分以下几种情况讨论:
①如图1,以点M为圆心,B′M长为半径画圆交x轴于一点P,此时MP=MB′=5,
∴,
∴P(4,0);
②如图2,以点B′为圆心,B′M长为半径画圆交x轴于一点P,此时MP=MB′=5,
∴OP=9或1,
∴P(﹣9,0)或(1,0);
③如图3,作线段B′M的垂直平分线交x轴于一点P,此时MP=PB′,
设OP=x,则MP=B′P=4﹣x,
根据勾股定理得32+x2=(4﹣x)2,
解得:,
∴.
综合上述,点P的坐标为(4,0)或(﹣9,0)或(1,0)或.
(4)N(56,0);理由如下:
如图4:作∠ABN=45°,作AK⊥BN垂足为K,
∴∠KAB=∠ABN=45°,
∴BK=AK,
∵AB=10,AB2=BK2+AK2,
∴102=2AK2,
解得:,
∴,
设AN=x,则,
∴,
∵ON=6+x,
∴BN2=OB2+ON2,
∴,
解得:x=50或(不合题意,舍去),
∴ON=6+50=56,
∴N(56,0).
5.【解答】解:(1)将点A(2,3)代入一次函数,
得1+b=3,
∴b=2,
∴y=x+2,
当x=0时,y=2,
∴点B坐标为(0,2),
当y=x+2=0时,x=﹣4,
∴点C坐标为(﹣4,0);
(2)作点B关于x轴的对称点D,连接AD,交x轴于点P′,当点P与点P′重合时,
此时PA+PB最小,
∵点B坐标为(0,2),
∴点D坐标为(0,﹣2),
设直线AD的解析式为y=mx+n(m≠0,m,n为常数),
代入A(2,3),D(0,﹣2),
得,
解得,
∴直线AD的解析式为,
当=0时,x=,
∴点P′坐标为(,0),
∴PA+PB最小时,点P坐标为(,0);
(3)∵点C坐标为(﹣4,0),
∴CP==,
∴S△ABP=S△ACP﹣S△BCP
=
=.
6.【解答】解:(1)直线AB的解析式为y=kx+3,D点的坐标为(4,0),把x=0代入y=kx+3,得:y=3,
∴点A的坐标为(0,3),
∴OA=3,OD=4,
∵∠AOD=90°,
在直角三角形OAD中,由勾股定理得:,
∵点O关于直线AB的对称点C在直线AD上,
∴OA=AC=3,OB=BC,
∴CD=AD﹣AC=2,
设OB=BC=a,则BD=4﹣a,
在Rt△BCD中,由勾股定理得:BD2=BC2+CD2,
∴(4﹣a)2=a2+22,
解得,
∴点B的坐标为,
把代入y=kx+3,得:
,
解得k=﹣2,
∴直线AB的解析式为y=﹣2x+3;
(2)点P是直线AB上方第一象限内的动点,当△ABP为等腰直角三角形时,分以下三种情况讨论:
①若∠PAB=90°,AP=AB,过点P作PM⊥y轴,垂足为M,如图1,
∵∠MAP+∠APM=90°,∠MAP+∠BAO=90°,
∴∠APM=∠BAO,
∵∠PMA=∠AOB=90°,PA=AB,
∴△APM≌△BAO(AAS),
∴,
∴,
∴点P的坐标为;
②若∠ABP=90°,BA=BP,如图2,过点P作PM⊥x轴,垂足为M,
∵∠ABO+∠BAO=90°,∠ABO+∠PBM=90°,
∴∠BAO=∠PBM,
∵∠AOB=∠BMP=90°,BA=BP,
∴△AOB≌△BMP(AAS),
∴,
∴,
∴点P的坐标为;
③若∠APB=90°,PA=PB,如图3,过点P作直线垂直x轴,交x轴于N,过点A作AM⊥PN,垂足为M,
设点P的坐标为(m,n),
∵∠APM+∠PAM=90°,∠APM+∠BPN=90°,
∴∠PAM=∠BPN,
∵∠AMP=∠PNB=90°,PA=PB,
∴△APM≌△PBN(AAS),
∴AM=PN,PM=BN,
即,
解得,
∴点P的坐标为;
综上所述,点P的坐标为或或.
7.【解答】解:(1)在y=2x+3中,当x=0时,y=3,
在y=﹣2x﹣3中,当x=0时,y=﹣3,当y=0时,,
∴,
∴,
∴;
(2)联立,
解得,
∴D点的坐标是(﹣3,3),
设点E的坐标为(t,0),则,DE2=(﹣3﹣t)2+(3﹣0)2,
∵△BDE是以BD为底边的等腰三角形,
∴BE=DE,
∴BE2=DE2,
∴,
∴,
解得,
∴;
(3)如图,当点P在点A的下方,
∵A(0,3),D(﹣3,3),
∴AD=OA,AD⊥y轴,
∴∠ADO=∠ADP+∠PDO=45°,
∵∠ODB=∠PDA,
∴∠PDB=∠ODB+∠PDO=45°;
过点B作BN⊥BD交直线DP于点N,过点N作NQ⊥OB于点Q,过点D作DH⊥OB于点H,
∴△DBN为等腰直角三角形,
∴DB=BN,
∵∠BDH+∠DBH=90°,∠DBH+∠NBQ=90°,
∴∠BDH=∠NBQ,
在△DHB和△BQN中,
,
∴△DHB≌△BQN(AAS),
∴,BQ=DH=3,
∴,
∴,
设直线DN的解析式为y=kx+b,
∴,
解得:,
∴直线DN的解析式为,
联立直线AB和DN解析式得到,
解得:即,.
8.【解答】解:(1)∵直线y=kx﹣8k交x轴于点A,交y轴正半轴于点B,
∴点A(8,0),B(0,﹣8k),
∴OA=8,OB=﹣8k,
∵△AOB的面积等于32,
∴S△AOB=,
∴k=﹣1,
∴直线AB的解析式为y=﹣x+8;
(2)∵把线段PB绕点B顺时针旋转90°得到线段CB,
∴PB=BC,∠PBC=90°,
∴∠CBE+∠PBE=90°,
如图,过点C作CE⊥y轴于点E,
则∠CEB=90°,
∴∠BCE+∠CBE=90°,
∴∠BCE=∠PBE,
在△CEB和△BOP中,
,
∴△CEB≌△BOP(AAS),
∴CE=BO=8,BE=OP=m,
∴OE=OB﹣BE=8﹣m,
∴C(﹣8,8﹣m);
(3)如图,延长BD至N,使DN=AD,过点N作NK⊥x轴于K,连接AN,
∵BC=BP,∠CBP=90°,
∴∠BCP=∠BPC=45°,
同理∠BAO=45°,
设∠CPE=α,则∠E=∠BCP﹣CPE=45°﹣α,
∵3∠CPE+∠BAD=90°,
∴∠BAD=90°﹣3α,
∵∠DBA=∠E+∠BAO,
∴∠DBA=90°﹣α,
∴∠ADB=180°﹣∠DBA﹣∠BAD=4α,
∵DN=AD,
∴∠DNA=∠DAN=2α,
∴∠NAB=∠DAN+∠BAD=90°﹣3α+2α=90°﹣α,
∴∠DBA=∠NAB,
∴NB=NA,
∵AD+BD=BE,
∴DN+BD=BE=BN
∴NA=BE,
在Rt△ENK中,∠ENK=90°﹣∠E=45°+α,
∴∠ANK=∠ENK﹣∠ANB=45°+α﹣2α=45°﹣α,
∴∠ANK=∠E,
∵∠EOB=∠NKA=90°,
在△EOB和△NKA中,
,
∴△EOB≌△NKA(AAS),
∴AK=OB=8,EO=NK,
∴△EOB∽△EKN,
∴,
∴EO=NK=16,
∴E(﹣16,0),N(16,16),
设直线EB表达式为y=kx+b,
则,
解得,
∴直线EB表达式为,
设,
∵DA=DN,
∴,
解得d=6,
∴D(6,11),
如图,过点D作DR⊥x轴于点R,Q作QS⊥x轴于点S,过点P作PT⊥AD于点T,
则DR=11,AR=8﹣6=2,
由勾股定理得,
∴,,,
而∠BPO=45°+α,则∠OBP=∠E=45°﹣α,
∴,
∴OP=4,则AP=4,
∴,,
∵∠PQA=45°,
∴,
∴,
∴,,
∴,
∴.
9.【解答】解:(1)因为一次函数y=kx+b(k≠0)的图象由函数y=2x的图象平移得到,
所以k=2.
将点(﹣1,3)的坐标代入y=2x+b得,
﹣2+b=3,
解得b=5,
所以一次函数的解析式为y=2x+5.
(2)将x=0代入y=2x+5得,
y=5,
所以点B的坐标为(0,5).
将y=0代入y=2x+5得,
x=,
所以点A的坐标为().
(3)因为△OAP的面积为5,
所以,
解得y=±4.
当y=4时,
2x+5=4,
解得x=,
所以点P的坐标为().
当y=﹣4时,
2x+5=﹣4,
解得x=,
所以点P的坐标为(),
综上所述,点P的坐标为()或().
10.【解答】解:(1)∵+|a+1|=0,
∴=0,|a+1|=0,
∴b﹣3=0,a+1=0,
∴a=﹣1,b=3,
∴A(﹣1,0),B(3,0).
(2)∵点M为第三象限内的一点,
∴m<0,
∵AB=|﹣1﹣3|=4,
∴△ABM的面积为AB (﹣m)=﹣2m.
(3)∵点M为第三象限内的一点,且点M(2﹣m,2m﹣10)到坐标轴的距离相等,
∴2﹣m=2m﹣10,
∴m=4,
∴M(﹣2,﹣2),
∵MN∥AB,AB=4,
∴﹣2﹣4=﹣6,﹣2+4=2,
∴点N的坐标是(2,﹣2)或(﹣6,﹣2).
11.【解答】解:(1)把A(6,0),B(0,6)代入y=kx+b得:
,
解得,
故答案为:﹣1,6;
(2)如图:
∵A(6,0),B(0,6),
∴线段AB的中点P的坐标为(3,3),
把P(3,3)代入y=x+c得:3=+c,
解得c=,
∴直线l2的解析式为y=x+,
由(1)知直线l1的解析式为y=﹣x+6,
∵Q(t,0),QD⊥x轴,
∴D(t,﹣t+6),E(t,t+),
∴DE=|﹣t+6﹣(t+)|=|﹣t+|,DQ=|﹣t+6|,
∵△ODE和△ODQ,其中一个三角形面积是另一个三角形面积的两倍,
∴DE=2DQ或DQ=2DE,
∴|﹣t+|=2|﹣t+6|或|﹣t+6|=2|﹣t+|,
∴﹣t+=2(﹣t+6)或﹣t+=﹣2(﹣t+6)或﹣t+6=2(﹣t+)或﹣t+6=﹣2(﹣t+),
解得t=15或t=或t=或t=;
(3)作M关于y轴的对称点G(2,0),以G为直角顶点,BG为直角边在BG右侧作等腰直角三角形BGH,过H作HK⊥x轴于K,如图:
∴∠OBM=∠OBG,
∵A(6,0),B(0,6),
∴△AOB是等腰直角三角形,
∴∠OBG+∠ABG=45°,
∵△BGH是等腰直角三角形,
∴∠ABG+∠ABH=45°,BG=GH,
∴∠OBG=∠ABH,
∴∠OBM=∠ABH,
∴N在直线BH上,
∵∠OGB=90°﹣∠HGK=∠GHK,∠BOG=∠GKH=90°,BG=GH,
∴△BOG≌△GKH(AAS),
∴BO=GK=6,OG=HK=2,
∴H(8,2),
由B(0,6),H(8,2)可得直线BH解析式为y=﹣x+6,
把N(m,2m﹣6)代入得:
2m﹣6=﹣m+6,
解得m=.
12.【解答】解:(1)在y=2x+4中,令x=0,y=4,令y=0,x=﹣2,
∴B(﹣2,0),
设直线BC的解析式为y=kx+b,
∴,
∴,
∴直线BC的解析式为y=﹣2x﹣4;
(2)联立,
解得,
∴D点的坐标是(﹣4,4),
设点E的坐标为(t,0),则BE2=(﹣2﹣t)2,DE2=(﹣4﹣t)2+(4﹣0)2,
∵△BDE是以BD为底边的等腰三角形,
∴BE=DE,
∴BE2=DE2,
∴(﹣2﹣t)2=(﹣4﹣t)2+(4﹣0)2,
解得t=﹣,
∴E(﹣,0),
∴OE=;
设E(0,t),则BE2=4+t2,DE2=(﹣4﹣0)2+(4﹣t)2,
∵△BDE是以BD为底边的等腰三角形,
∴BE=DE,
∴BE2=DE2,
∴4+t2=(﹣4﹣0)2+(4﹣t)2,
解得t=,
∴E(0,),
∴OE=;
(3)如图,当点P在点A的下方,
∵A(0,4),D(﹣4,4),
∴AD=OA,AD⊥y轴,
∴∠ADO=∠ADP+∠PDO=45°,
∵∠ODB=∠PDA,
∴∠PDB=∠ODB+∠PDO=45°;
过点B作BN⊥BD交直线DP于点N,过点N作NQ⊥OB于点Q,过点D作DH⊥OB于点H,
∴△DBN为等腰直角三角形,
∴DB=BN,
∵∠BDH+∠DBH=90°,∠DBH+∠NBQ=90°,
∴∠BDH=∠NBQ,
在△DHB和△BQN中,
,
∴△DHB≌△BQN(AAS),
∴NQ=BH=﹣2﹣(﹣4)=2,BQ=DH=4,
∴OQ=BQ﹣BO=2,
∴N(2,2),
设直线DN的解析式为y=kx+b,
∴,
解得,
∴直线DN的解析式为y=﹣x+,
当x=0时,y=,
∴P(0,).
13.【解答】解:(1)∵直线l2:与x轴、y轴分别交于点A、点B,
故把x=0,则y=3;
把y=0,则x=6,
∴与x轴、y轴分别交于点A、点B坐标分别为(6,0)、(0,3),
∵直线l1与l2交于点C,
联立得方程组:两个函数表达式得:﹣x+3=x,
解得:x=2,
故点C(2,2);
则△COB的面积=OB×xC==3;
(2)①设点M、N的坐标分别为(m,m)、(m,3﹣m),
根据题意可得:|m﹣(3﹣m)|=2,
解得:m=或m=,
所以点N的坐标为: 或,
故答案为: 或;
②y轴上存在点Q,使△MNQ为等腰直角三角形,理由如下:
设M、N、Q的坐标分别为(m,m)、(m,3﹣m)、(0,n),
当∠MQN=90°时,
如图1.2,作PQ⊥MN交MN于点P,
由题意得:MN=2PQ,
∴﹣m+3﹣m=2m,
解得:m=,
∴Q点坐标为:(0,);
当∠QNM=90°时,如图2:
则MN=QN,即:3﹣m﹣m=m,
解得:m=,
∴Q点坐标为:(0,);
当∠NMQ=90°时,如图3:
则MN=QM,即:3﹣m﹣m=m,
解得:m=,
∴Q点坐标为:(0,),
综上,点Q的坐标为:.
14.【解答】解:(1)在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(3,0),B(0,4),
∴OA=3,OB=4,
在Rt△AOB中,由勾股定理得:AB==5,
由折叠的性质可知,AD=AB=5,
∴OD=OA+AD=3+5=8,
∴点D的坐标是(8,0),
设OC=x,则BC=OB+OC=4+x,
由折叠的性质可知,CD=BC=4+x,
在Rt△COD中,由勾股定理得:OC2+OD2=CD2,
∴x2+82=(x+4)2,
解得:x=6,即OC=6,
∴点C的坐标为(0,﹣6);
由C、D的坐标得,直线CD的表达式为:y=x﹣8,
同理可得:直线AB的表达式为:y=x+4,
故直线BE与直线CD的位置关系是垂直,
故答案为:5,(8,0),垂直;
(2)由(1)得,点C的坐标为(0,﹣6);
(3)∵C(0,﹣6),D(8,0),
∴OC=6,OD=8,
则S△COD===24,
则S△MAB=12,
∵点M是y轴上一动点,
∴设点M的坐标为(0,m),
∴BM=|m﹣4|,
则S△MAB=BM OA=|m﹣4|×3=12,
∴m=12或﹣4,
∴点M的坐标为(0,12)或(0,﹣4);
(4)在第一象限内存在点P,使△PAB为等腰直角三角形;理由如下:
①当∠BAP=90°,AB=AP,则△PAB为等腰直角三角形,
如图1,过点P作PG⊥x轴于点G,
∴∠PGA=∠AOB=90°,
∵∠BAP=90°,
∴∠BAO+∠PAG=90°,
∵∠ABO+∠BAO=90°,
∴∠ABO=∠PAG,
在△AOB和△PGA中,∠ABO=∠PAG,∠AOB=∠PGA,AB=PA,
∴△AOB≌△PGA(AAS),
∴OA=PG=3,OB=AG=4,
∴OG=OA+AG=7,
∴点P的坐标为(7,3);
②当∠ABP=90°,BA=BP,则△PAB为等腰直角三角形,
如图2,过点P作PH⊥y轴于点H,
同理 可证,△AOB≌△BHP(AAS),
∴OA=BH=3,PH=OB=4,
∴OH=OB+BH=7,
∴点P的坐标为(4,7);
③当∠APB=90°,PA=PB,则△PAB为等腰直角三角形,
如图3,过点P作PM⊥x轴于点M,PN⊥y轴于点N,
∴∠PNB=∠PMA=∠MPN=90°,
∴∠APN+∠APM=90°,
∵∠APB=90°,
∴∠BPN+∠APN=90°,
∴∠APM=∠BPN,
在△APM和△BPN中,∠APM=∠BPN,PA=PB,∠PMA=∠PNB,
∴△APM≌△BPN(ASA),
∴AM=BN,PM=PN,
∴设点P的坐标为(p,p),
∴OM=ON=p,
∴BN=OB﹣ON=4﹣p,AM=OM﹣OA=p﹣3,
∴4﹣p=p﹣3,
解得:p=,
则点P的坐标为(,),
综上可知,第一象限内存在点P,使△PAB为等腰直角三角形,点P的坐标(7,3)或(4,7)或(,).
15.【解答】解:(1)在y=﹣2x+4中,令x=0得y=4,令y=0得x=2,
∴A(2,0),B(0,4),
设直线m的解析式为y=kx+b,把M(1,2),C(﹣1,0)代入得:
,
解得,
∴直线m的解析式为y=x+1;
(2)在y=x+1中,令x=0得y=1,令y=0得x=﹣1,
∴C(﹣1,0),D(0,1),
∵B(0,4),
∴BD=3,
∵M(1,2),
∴S△BDM=×3×1=,
∵S△APM=2S△BDM,
∴S△APM=3;
∵A(2,0),C(﹣1,0),
∴AC=3,
∵M(1,2),
∴S△ACM=×3×2=3;
①当P与C重合时,S△APM=S△ACM=3=2S△BDM,此时P(﹣1,0);
②当P在AB右侧时,S△APC=S△APM+S△ACM=3+3=6,
∴×3 yP=6,
∴yP=4,
在y=x+1中,令y=4得x=3,
∴P(3,4);
综上所述,P的坐标为(﹣1,0)或(3,4);
(3)设Q(p,q),
∵A(2,0),B(0,4),
∴QA2=(p﹣2)2+q2,QB2=p2+(q﹣4)2,AB2=20,
①当QA为等腰直角三角形斜边时,QA2=2AB2,QB2=AB2,
∴,
解得(此时Q不在第一象限,舍去)或,
∴Q(4,6);
②当QB为等腰直角三角形斜边时,QB2=2AB2,QA2=AB2,
∴,
解得或(舍去),
∴Q(6,2);
③当AB为等腰直角三角形斜边时,QA2=AB2,QA2=QB2,
∴,
解得(舍去)或,
∴Q(3,3);
综上所述,Q的坐标为(4,6)或(6,2)或(3,3).
21世纪教育网(www.21cnjy.com)
同课章节目录
