北师大版七年级数学下册单元质量评价(一)课件
文档属性
| 名称 | 北师大版七年级数学下册单元质量评价(一)课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:16:00 | ||
图片预览








文档简介
(共21张PPT)
单元质量评价(一)
(第一章)
(时间45分钟 满分100分)
一、选择题:本大题共5小题,每小题5分,共25分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2024·深圳实验中学期末)下列各式中,运算正确的是( )
A.a2+2a3=3a5 B.a2·a3=a6
C.(-a2)4=-a8 D.a8÷a2=a6
【解析】A.a2与a3不是同类项,不能合并,故本选项不符合题意;
B.a2·a3=a2+3=a5,故本选项不符合题意;
C.应为(-a2)4=(-1)4a8=a8,故本选项不符合题意;
D.a8÷a2=a8-2=a6,故本选项符合题意.
D
2.“春江潮水连海平,海上明月共潮生.”水是诗人钟爱的意象,经测算,一个水分子的直
径约为0.000 000 000 4 m,数据0.000 000 000 4用科学记数法表示为( )
A.4×10-11 B.4×10-10
C.4×10-9 D.0.4×10-9
【解析】0.000 000 000 4=4×10-10.
B
3.(2024·深圳红岭教育集团期中)下列能用平方差公式计算的是( )
A.(-x+y)(-x+y) B.(-x-y)(x-y)
C.(x-1)(1-x) D.(2x+1)(x-2)
【解析】A.应为(-x+y)(-x+y)=(-x+y)2,故本选项不符合题意;
B.(-x-y)(x-y)=y2-x2,故本选项符合题意;
C.(x-1)(1-x)=-(x-1)2,故本选项不符合题意;
D.(2x+1)(x-2)=2x2-3x-2,故本选项不符合题意.
B
4.已知2x+y=1,则4x×2y的值为( )
A.2 B.4 C.16 D.32
【解析】因为2x+y=1,
所以4x×2y=(22)x×2y
=22x×2y
=22x+y
=21
=2.
A
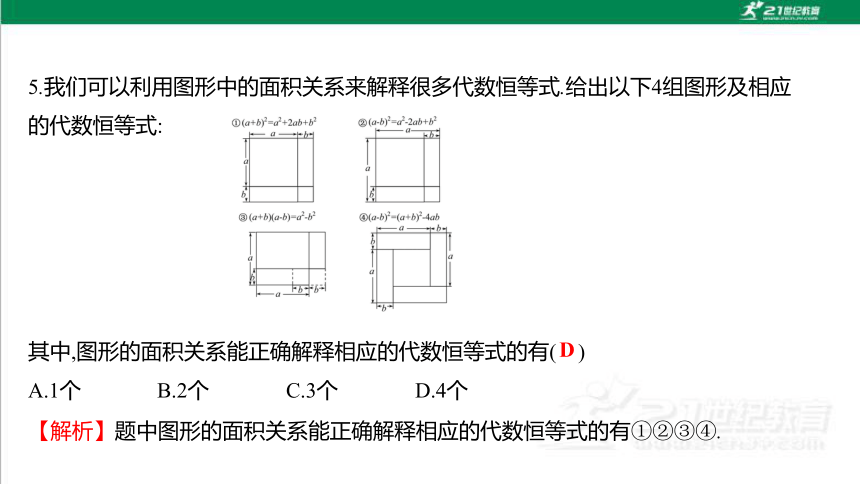
5.我们可以利用图形中的面积关系来解释很多代数恒等式.给出以下4组图形及相应的代数恒等式:
其中,图形的面积关系能正确解释相应的代数恒等式的有( )
A.1个 B.2个 C.3个 D.4个
【解析】题中图形的面积关系能正确解释相应的代数恒等式的有①②③④.
D
二、填空题:本大题共5小题,每小题5分,共25分.
6.比较大小:2-2______30.(选填“>”“=”“<”)
<
7.若82=42×2m,则m=______.
【解析】因为82=42×2m,
所以26=24×2m,所以26=24+m,
所以6=4+m,解得m=2.
2
8.(2024·深圳中学期末)若a+b=3,ab=1,则a2+b2=______.
【解析】因为a+b=3,ab=1,
所以a2+b2=(a+b)2-2ab=9-2=7.
7
9.(2024·揭阳惠来一中期末)七年级一班教室的后墙上的“学习园地”是一个长方形,它的
面积为(3x)3-6ax2-3x,其中一边长为3x,则这个“学习园地”的另一边长为_____________.
【解析】因为长方形面积是(3x)3-6ax2-3x,一边长为3x,
所以它的另一边长是[(3x)3-6ax2-3x]÷3x
=(27x3-6ax2-3x)÷3x
=9x2-2ax-1.
9x2-2ax-1
10.如图所示,在长方形ABCD中,AB=6,点E,F是边BC,CD上的点,EC=3,且BE=DF=x,分
别以FC,CB为边在长方形ABCD外侧作正方形CFGH和CBMN,若长方形CBQF的面积
为20,则图中阴影部分的面积和为_______.
【解析】设CF=a,BC=b,由题意得,FC=6-x,BC=3+x,
即a=6-x,b=3+x,
因为长方形CBQF的面积为20,所以ab=(6-x)(3+x)=20,
又因为a+b=(6-x)+(x+3)=9,
所以S阴影=CF2+BC2=a2+b2=(a+b)2-2ab
=92-2×20=41,
所以阴影部分的面积和为41.
41
12.(10分)(1)先化简,再求值:(x+y)2+x(x-2y),其中x=1,y=-2.
(2)先化简,再求值:(3x-y)2-(x+y)(x-y)-2y2,其中x=3,y=-1.
【解析】(1)原式=x2+2xy+y2+x2-2xy=2x2+y2,当x=1,y=-2时,
原式=2×12+(-2)2=6.
(2)(3x-y)2-(x+y)(x-y)-2y2=9x2-6xy+y2-(x2-y2)-2y2
=9x2-6xy+y2-x2+y2-2y2=8x2-6xy,
当x=3,y=-1时,原式=8×32-6×3×(-1)
=8×9+18=72+18
=90.
13.(10分)某中学九年级的学生人数比八年级学生多.做广播体操时,九年级排成的是一个规范的长方形方阵,每排(3a+b)人,有(2a+2b)排;八年级站的是正方形方阵,排数和每排人数都是2(a+b),其中a>b.
(1)试求该学校九年级比八年级多多少名学生,用含a与b的代数式表示.
(2)当a=10,b=2时,求该学校九年级比八年级多多少名学生.
【解析】(1)(3a+b)(2a+2b)-[2(a+b)]2
=6a2+6ab+2ab+2b2-4(a2+2ab+b2)
=6a2+6ab+2ab+2b2-4a2-8ab-4b2
=2a2-2b2,
则该学校九年级比八年级多(2a2-2b2)名学生.
(2)当a=10,b=2时,
由(1)得,原式=2×102-2×22=192.
答:该学校九年级比八年级多192名学生.
14.(10分)(2024·茂名质检)特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立刻说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C)且B+C=10,当A>3时,那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2 021,61×69=4 209.
(1)请你直接写出84×86的值;
(2)若设一个两位数的十位上的数字为m,个位上的数字为n,则另一个两位数的个位上的数字为 ;用含m,n的等式表示以上两位数相乘的规律 ;
(3)请用所学知识证明(2)中的规律.
【解析】(1)84和86满足题中的条件,即十位数都是8,且8>3,个位数字分别是4和6,和为10,所以它们的乘积是一个4位数,前两位数字是8和9的乘积,后两位数字就是4和6的乘积,所以84×86=8×9×100+4×6=7 224.
(2)一个两位数的十位上的数字为m,个位上的数字为n,则另一个两位数的个位上的数字为10-n,用含m,n的等式表示以上两位数相乘的规律为:(10m+n)[10m+(10-n)]= 100m(m+1)+n(10-n).
答案:10-n (10m+n)[10m+(10-n)]=100m(m+1)+n(10-n)
(3)因为(10m+n)[10m+(10-n)]
=(10m+n)(10m-n+10)
=100m2-10mn+100m+10mn-n2+10n
=(100m2+100m)+(10n-n2)
=100m(m+1)+n(10-n),
所以(10m+n)[10m+(10-n)]=100m(m+1)+n(10-n).
单元质量评价(一)
(第一章)
(时间45分钟 满分100分)
一、选择题:本大题共5小题,每小题5分,共25分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2024·深圳实验中学期末)下列各式中,运算正确的是( )
A.a2+2a3=3a5 B.a2·a3=a6
C.(-a2)4=-a8 D.a8÷a2=a6
【解析】A.a2与a3不是同类项,不能合并,故本选项不符合题意;
B.a2·a3=a2+3=a5,故本选项不符合题意;
C.应为(-a2)4=(-1)4a8=a8,故本选项不符合题意;
D.a8÷a2=a8-2=a6,故本选项符合题意.
D
2.“春江潮水连海平,海上明月共潮生.”水是诗人钟爱的意象,经测算,一个水分子的直
径约为0.000 000 000 4 m,数据0.000 000 000 4用科学记数法表示为( )
A.4×10-11 B.4×10-10
C.4×10-9 D.0.4×10-9
【解析】0.000 000 000 4=4×10-10.
B
3.(2024·深圳红岭教育集团期中)下列能用平方差公式计算的是( )
A.(-x+y)(-x+y) B.(-x-y)(x-y)
C.(x-1)(1-x) D.(2x+1)(x-2)
【解析】A.应为(-x+y)(-x+y)=(-x+y)2,故本选项不符合题意;
B.(-x-y)(x-y)=y2-x2,故本选项符合题意;
C.(x-1)(1-x)=-(x-1)2,故本选项不符合题意;
D.(2x+1)(x-2)=2x2-3x-2,故本选项不符合题意.
B
4.已知2x+y=1,则4x×2y的值为( )
A.2 B.4 C.16 D.32
【解析】因为2x+y=1,
所以4x×2y=(22)x×2y
=22x×2y
=22x+y
=21
=2.
A
5.我们可以利用图形中的面积关系来解释很多代数恒等式.给出以下4组图形及相应的代数恒等式:
其中,图形的面积关系能正确解释相应的代数恒等式的有( )
A.1个 B.2个 C.3个 D.4个
【解析】题中图形的面积关系能正确解释相应的代数恒等式的有①②③④.
D
二、填空题:本大题共5小题,每小题5分,共25分.
6.比较大小:2-2______30.(选填“>”“=”“<”)
<
7.若82=42×2m,则m=______.
【解析】因为82=42×2m,
所以26=24×2m,所以26=24+m,
所以6=4+m,解得m=2.
2
8.(2024·深圳中学期末)若a+b=3,ab=1,则a2+b2=______.
【解析】因为a+b=3,ab=1,
所以a2+b2=(a+b)2-2ab=9-2=7.
7
9.(2024·揭阳惠来一中期末)七年级一班教室的后墙上的“学习园地”是一个长方形,它的
面积为(3x)3-6ax2-3x,其中一边长为3x,则这个“学习园地”的另一边长为_____________.
【解析】因为长方形面积是(3x)3-6ax2-3x,一边长为3x,
所以它的另一边长是[(3x)3-6ax2-3x]÷3x
=(27x3-6ax2-3x)÷3x
=9x2-2ax-1.
9x2-2ax-1
10.如图所示,在长方形ABCD中,AB=6,点E,F是边BC,CD上的点,EC=3,且BE=DF=x,分
别以FC,CB为边在长方形ABCD外侧作正方形CFGH和CBMN,若长方形CBQF的面积
为20,则图中阴影部分的面积和为_______.
【解析】设CF=a,BC=b,由题意得,FC=6-x,BC=3+x,
即a=6-x,b=3+x,
因为长方形CBQF的面积为20,所以ab=(6-x)(3+x)=20,
又因为a+b=(6-x)+(x+3)=9,
所以S阴影=CF2+BC2=a2+b2=(a+b)2-2ab
=92-2×20=41,
所以阴影部分的面积和为41.
41
12.(10分)(1)先化简,再求值:(x+y)2+x(x-2y),其中x=1,y=-2.
(2)先化简,再求值:(3x-y)2-(x+y)(x-y)-2y2,其中x=3,y=-1.
【解析】(1)原式=x2+2xy+y2+x2-2xy=2x2+y2,当x=1,y=-2时,
原式=2×12+(-2)2=6.
(2)(3x-y)2-(x+y)(x-y)-2y2=9x2-6xy+y2-(x2-y2)-2y2
=9x2-6xy+y2-x2+y2-2y2=8x2-6xy,
当x=3,y=-1时,原式=8×32-6×3×(-1)
=8×9+18=72+18
=90.
13.(10分)某中学九年级的学生人数比八年级学生多.做广播体操时,九年级排成的是一个规范的长方形方阵,每排(3a+b)人,有(2a+2b)排;八年级站的是正方形方阵,排数和每排人数都是2(a+b),其中a>b.
(1)试求该学校九年级比八年级多多少名学生,用含a与b的代数式表示.
(2)当a=10,b=2时,求该学校九年级比八年级多多少名学生.
【解析】(1)(3a+b)(2a+2b)-[2(a+b)]2
=6a2+6ab+2ab+2b2-4(a2+2ab+b2)
=6a2+6ab+2ab+2b2-4a2-8ab-4b2
=2a2-2b2,
则该学校九年级比八年级多(2a2-2b2)名学生.
(2)当a=10,b=2时,
由(1)得,原式=2×102-2×22=192.
答:该学校九年级比八年级多192名学生.
14.(10分)(2024·茂名质检)特殊两位数乘法的速算——如果两个两位数的十位数字相同,个位数字相加为10,那么能立刻说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC(即十位数字为A,个位数字分别为B、C)且B+C=10,当A>3时,那么它们的乘积是一个4位数,前两位数字是A和(A+1)的乘积,后两位数字就是B和C的乘积.
如:47×43=2 021,61×69=4 209.
(1)请你直接写出84×86的值;
(2)若设一个两位数的十位上的数字为m,个位上的数字为n,则另一个两位数的个位上的数字为 ;用含m,n的等式表示以上两位数相乘的规律 ;
(3)请用所学知识证明(2)中的规律.
【解析】(1)84和86满足题中的条件,即十位数都是8,且8>3,个位数字分别是4和6,和为10,所以它们的乘积是一个4位数,前两位数字是8和9的乘积,后两位数字就是4和6的乘积,所以84×86=8×9×100+4×6=7 224.
(2)一个两位数的十位上的数字为m,个位上的数字为n,则另一个两位数的个位上的数字为10-n,用含m,n的等式表示以上两位数相乘的规律为:(10m+n)[10m+(10-n)]= 100m(m+1)+n(10-n).
答案:10-n (10m+n)[10m+(10-n)]=100m(m+1)+n(10-n)
(3)因为(10m+n)[10m+(10-n)]
=(10m+n)(10m-n+10)
=100m2-10mn+100m+10mn-n2+10n
=(100m2+100m)+(10n-n2)
=100m(m+1)+n(10-n),
所以(10m+n)[10m+(10-n)]=100m(m+1)+n(10-n).
同课章节目录
