北师大版七年级数学下册单元质量评价(二)课件
文档属性
| 名称 | 北师大版七年级数学下册单元质量评价(二)课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:16:00 | ||
图片预览







文档简介
(共28张PPT)
单元质量评价(二)
(第二章)
(时间45分钟 满分100分)
一、选择题:本大题共5小题,每小题5分,共25分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2024·揭阳榕城期中)如图所示,∠1和∠2( )
A.是同位角 B.是内错角
C.是同旁内角 D.互为补角
C
【解析】由题图可知,
∠1和∠2是同旁内角.
2.(2024·珠海香洲期末)如图所示,河道l的一侧有A,B两个村庄,现要铺设一条引水管
道把河水引向A,B两村,下列四种方案中,最节省材料的是( )
B
【解析】依据垂线段最短,以及两点之间,线段最短,可得最节省材料的是B.
3.(2024·中山期中)如图所示,下列条件中,不能判断直线AD∥BC的是( )
A.∠1=∠3 B.∠3=∠E
C.∠2=∠B D.∠BCD+∠D=180°
A
【解析】由∠1=∠3,不能判定AD∥BC,故A符合题意;
因为∠3=∠E,所以AD∥BC,故B不符合题意;
因为∠2=∠B,所以AD∥BC,
故C不符合题意;
因为∠BCD+∠D=180°,
所以AD∥BC,
故D不符合题意.
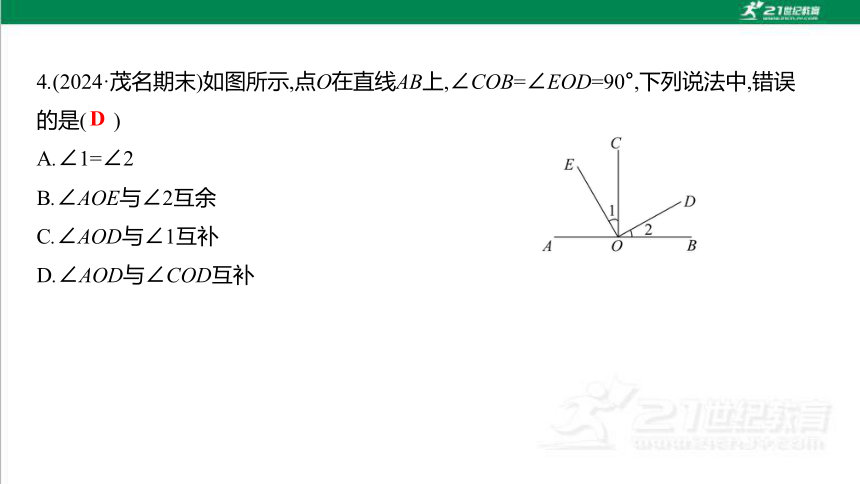
4.(2024·茂名期末)如图所示,点O在直线AB上,∠COB=∠EOD=90°,下列说法中,错误
的是( )
A.∠1=∠2
B.∠AOE与∠2互余
C.∠AOD与∠1互补
D.∠AOD与∠COD互补
D
【解析】因为∠COB=∠EOD=90°,所以∠1+∠COD=∠2+∠COD=90°,
所以∠1=∠2,故A选项正确;
因为∠AOE+∠1=90°,
所以∠AOE+∠2=90°,
即∠AOE与∠2互余,故B选项正确;
因为∠AOD+∠2=180°,∠1=∠2,
所以∠AOD+∠1=180°,即∠AOD与∠1互补,故C选项正确;
无法判断∠AOD与∠COD是否互补,D选项错误.
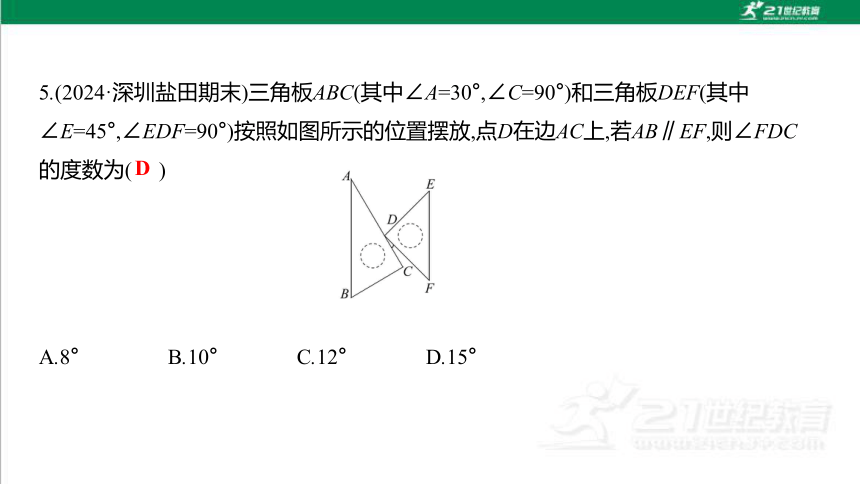
5.(2024·深圳盐田期末)三角板ABC(其中∠A=30°,∠C=90°)和三角板DEF(其中
∠E=45°,∠EDF=90°)按照如图所示的位置摆放,点D在边AC上,若AB∥EF,则∠FDC
的度数为( )
A.8° B.10° C.12° D.15°
D
【解析】过D作DK∥AB,
因为AB∥EF,
所以DK∥EF,
所以∠ADK=∠A=30°,∠EDK=∠E=45°,
所以∠ADK+∠EDK=30°+45°=75°=∠ADE,
因为∠EDF=90°,
所以∠CDF=180°-90°-75°=15°.
二、填空题:本大题共5小题,每小题5分,共25分.
6.(2024·广州天河期末)如图所示,直线AB和CD相交于点O,OE⊥CD于点O,∠BOE=
2∠BOD,则∠AOC的度数为________.
30°
【解析】设∠BOD=x,则∠BOE=2x,
因为OE⊥CD,所以∠EOD=90°,
所以∠BOD+∠BOE=90°,
所以x+2x=90°,所以x=30°,
所以∠BOD=30°,
因为∠AOC=∠BOD,所以∠AOC=30°.
7.若一个角的补角是它的余角的3倍,则这个角的度数为________.
45°
【解析】设这个角的度数是x,
则180°-x=3(90°-x),
解得x=45°.
即这个角的度数是45°.
8.(2024·佛山期末)如图所示,DE∥BC,DF∥AC,若∠DFB=110°,则∠DEC的度数为
________.
70°
【解析】因为DF∥AC,∠DFB=110°,
所以∠C=∠DFB=110°,
因为DE∥BC,
所以∠DEC=180°-∠C=180°-110°=70°.
9.如图所示,MC∥AB,NC∥AB,则点M,C,N在同一条直线上,理由是_________________
_________________________________.
经过直线外一点,
有且只有一条直线与这条直线平行
【解析】因为MC∥AB,NC∥AB,所以点M,C,N在同一条直线上,理由是:经过直线外一点,有且只有一条直线与这条直线平行.
10.如图所示,在四边形ABCD中,∠A=50°,DB平分∠ADC,∠1+∠2=180°,且ED⊥DB.
下列判断中,正确的是___________(填序号).
①AB∥CD;②∠EDC=25°;③若AD∥BC,则∠1=130°;④若∠1=140°,则DE∥BC.
①②③
③因为AD∥BC,
所以∠A=∠2=50°,
因为∠1+∠2=180°,
所以∠1=130°;
④因为∠1=140°,
所以∠DCB=180°-140°=40°,
因为∠EDC=25°,所以不能推出DE∥BC.
三、解答题:共50分.
11.(10分)(2024·东莞期末)已知:如图所示,∠AOB=∠COD=180°,∠EOC=90°,OF平分∠AOE.
(1)∠AOE的余角是 .
(2)若∠BOC=40°,求∠COF的度数.
12.(10分)(2024·深圳龙岗区期中)如图所示,AD∥BC,点E是BA延长线上一点, ∠E=∠DCE.
(1)求证:∠B=∠D.
(2)若CE平分∠BCD,∠E=47°,求∠B的度数.
【解析】(1)因为AD∥BC,
所以∠B=∠EAD,
因为∠E=∠DCE,所以EB∥CD,
所以∠D=∠EAD,所以∠B=∠D.
(2)因为∠E=47°,∠E=∠DCE,
所以∠E=∠DCE=47°,
因为CE平分∠BCD,
所以∠BCE=∠DCE=47°,
所以∠B=180°-∠E-∠BCE=86°.
13.(10分)取一副三角板按如图1所示拼接,固定三角板ADC(∠ACD=30°),将三角板ABC(∠ACB=45°)绕点A依顺时针方向旋转一定的角度得到△ABC',请问:
(1)如图2所示,当∠CAC'=15°时,请你判断AB与CD的位置关系,并说明理由.
(2)如图3所示,当∠CAC'为多少度时,能使CD∥BC' (直接回答,不用证明)
【解析】(1)如图1所示,
因为∠BAC=∠BAC'-∠CAC'=45°-15°=30°,所以∠BAC=∠C=30°,
所以AB∥CD.
(2)当∠CAC'=75°时,能使CD∥BC',
理由如下:如图2所示,延长BA交CD于点E.因为CD∥BC',
所以∠B+∠AEC=180°,
因为∠B=90°,所以∠AEC=90°,
因为∠C=30°,所以∠CAE=60°,
所以∠C'AC=180°-(∠CAE+∠BAC')=180°-105°=75°.
14.(10分)图1是一辆滑轮摄影轨道车,图2为其侧面示意图.DE⊥GH于点E,BC与CD是轨道车的“手臂”,可通过改变∠BCD的度数调节车的高度,在调节过程中,放摄像机的杆AB始终平行于DE.
(1)如图3所示,调节轨道车的“手臂”,使BC∥GH,此时∠BCD=25°,求∠CDE的度数.
(2)若图2中∠BCD=45°,求∠ABC与∠CDE的度数之和.
【解析】(1)如图1所示,过点C作CP∥AB,且点P在BC的下方.
因为DE⊥GH,AB∥DE,
所以AB⊥GH.
因为BC∥GH,所以AB⊥BC,
所以∠BCP=∠B=90°,所以∠DCP=∠BCP-∠BCD=90°-25°=65°.
因为AB∥DE,CP∥AB,所以CP∥DE,所以∠CDE=180°-∠DCP=180°-65°=115°.
(2)如图2所示,过点C作CP∥AB,且点P在BC的下方.
因为CP∥AB,所以∠ABC=∠BCP=∠BCD+∠DCP.
易知CP∥DE,所以∠CDE+∠DCP=180°.
因为∠DCP=∠ABC-∠BCD,
所以∠CDE+∠ABC-∠BCD=180°,所以∠CDE+∠ABC=180°+∠BCD=225°.
15.(10分)已知AD∥BC,AB∥CD,E在线段BC的延长线上,AE平分∠BAD,连接DE, ∠ADE=3∠CDE.
(1)若∠AED=60°,求∠CDE的度数.
(2)若∠AEB=60°,探究DE与BE的位置关系,并说明理由.
单元质量评价(二)
(第二章)
(时间45分钟 满分100分)
一、选择题:本大题共5小题,每小题5分,共25分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(2024·揭阳榕城期中)如图所示,∠1和∠2( )
A.是同位角 B.是内错角
C.是同旁内角 D.互为补角
C
【解析】由题图可知,
∠1和∠2是同旁内角.
2.(2024·珠海香洲期末)如图所示,河道l的一侧有A,B两个村庄,现要铺设一条引水管
道把河水引向A,B两村,下列四种方案中,最节省材料的是( )
B
【解析】依据垂线段最短,以及两点之间,线段最短,可得最节省材料的是B.
3.(2024·中山期中)如图所示,下列条件中,不能判断直线AD∥BC的是( )
A.∠1=∠3 B.∠3=∠E
C.∠2=∠B D.∠BCD+∠D=180°
A
【解析】由∠1=∠3,不能判定AD∥BC,故A符合题意;
因为∠3=∠E,所以AD∥BC,故B不符合题意;
因为∠2=∠B,所以AD∥BC,
故C不符合题意;
因为∠BCD+∠D=180°,
所以AD∥BC,
故D不符合题意.
4.(2024·茂名期末)如图所示,点O在直线AB上,∠COB=∠EOD=90°,下列说法中,错误
的是( )
A.∠1=∠2
B.∠AOE与∠2互余
C.∠AOD与∠1互补
D.∠AOD与∠COD互补
D
【解析】因为∠COB=∠EOD=90°,所以∠1+∠COD=∠2+∠COD=90°,
所以∠1=∠2,故A选项正确;
因为∠AOE+∠1=90°,
所以∠AOE+∠2=90°,
即∠AOE与∠2互余,故B选项正确;
因为∠AOD+∠2=180°,∠1=∠2,
所以∠AOD+∠1=180°,即∠AOD与∠1互补,故C选项正确;
无法判断∠AOD与∠COD是否互补,D选项错误.
5.(2024·深圳盐田期末)三角板ABC(其中∠A=30°,∠C=90°)和三角板DEF(其中
∠E=45°,∠EDF=90°)按照如图所示的位置摆放,点D在边AC上,若AB∥EF,则∠FDC
的度数为( )
A.8° B.10° C.12° D.15°
D
【解析】过D作DK∥AB,
因为AB∥EF,
所以DK∥EF,
所以∠ADK=∠A=30°,∠EDK=∠E=45°,
所以∠ADK+∠EDK=30°+45°=75°=∠ADE,
因为∠EDF=90°,
所以∠CDF=180°-90°-75°=15°.
二、填空题:本大题共5小题,每小题5分,共25分.
6.(2024·广州天河期末)如图所示,直线AB和CD相交于点O,OE⊥CD于点O,∠BOE=
2∠BOD,则∠AOC的度数为________.
30°
【解析】设∠BOD=x,则∠BOE=2x,
因为OE⊥CD,所以∠EOD=90°,
所以∠BOD+∠BOE=90°,
所以x+2x=90°,所以x=30°,
所以∠BOD=30°,
因为∠AOC=∠BOD,所以∠AOC=30°.
7.若一个角的补角是它的余角的3倍,则这个角的度数为________.
45°
【解析】设这个角的度数是x,
则180°-x=3(90°-x),
解得x=45°.
即这个角的度数是45°.
8.(2024·佛山期末)如图所示,DE∥BC,DF∥AC,若∠DFB=110°,则∠DEC的度数为
________.
70°
【解析】因为DF∥AC,∠DFB=110°,
所以∠C=∠DFB=110°,
因为DE∥BC,
所以∠DEC=180°-∠C=180°-110°=70°.
9.如图所示,MC∥AB,NC∥AB,则点M,C,N在同一条直线上,理由是_________________
_________________________________.
经过直线外一点,
有且只有一条直线与这条直线平行
【解析】因为MC∥AB,NC∥AB,所以点M,C,N在同一条直线上,理由是:经过直线外一点,有且只有一条直线与这条直线平行.
10.如图所示,在四边形ABCD中,∠A=50°,DB平分∠ADC,∠1+∠2=180°,且ED⊥DB.
下列判断中,正确的是___________(填序号).
①AB∥CD;②∠EDC=25°;③若AD∥BC,则∠1=130°;④若∠1=140°,则DE∥BC.
①②③
③因为AD∥BC,
所以∠A=∠2=50°,
因为∠1+∠2=180°,
所以∠1=130°;
④因为∠1=140°,
所以∠DCB=180°-140°=40°,
因为∠EDC=25°,所以不能推出DE∥BC.
三、解答题:共50分.
11.(10分)(2024·东莞期末)已知:如图所示,∠AOB=∠COD=180°,∠EOC=90°,OF平分∠AOE.
(1)∠AOE的余角是 .
(2)若∠BOC=40°,求∠COF的度数.
12.(10分)(2024·深圳龙岗区期中)如图所示,AD∥BC,点E是BA延长线上一点, ∠E=∠DCE.
(1)求证:∠B=∠D.
(2)若CE平分∠BCD,∠E=47°,求∠B的度数.
【解析】(1)因为AD∥BC,
所以∠B=∠EAD,
因为∠E=∠DCE,所以EB∥CD,
所以∠D=∠EAD,所以∠B=∠D.
(2)因为∠E=47°,∠E=∠DCE,
所以∠E=∠DCE=47°,
因为CE平分∠BCD,
所以∠BCE=∠DCE=47°,
所以∠B=180°-∠E-∠BCE=86°.
13.(10分)取一副三角板按如图1所示拼接,固定三角板ADC(∠ACD=30°),将三角板ABC(∠ACB=45°)绕点A依顺时针方向旋转一定的角度得到△ABC',请问:
(1)如图2所示,当∠CAC'=15°时,请你判断AB与CD的位置关系,并说明理由.
(2)如图3所示,当∠CAC'为多少度时,能使CD∥BC' (直接回答,不用证明)
【解析】(1)如图1所示,
因为∠BAC=∠BAC'-∠CAC'=45°-15°=30°,所以∠BAC=∠C=30°,
所以AB∥CD.
(2)当∠CAC'=75°时,能使CD∥BC',
理由如下:如图2所示,延长BA交CD于点E.因为CD∥BC',
所以∠B+∠AEC=180°,
因为∠B=90°,所以∠AEC=90°,
因为∠C=30°,所以∠CAE=60°,
所以∠C'AC=180°-(∠CAE+∠BAC')=180°-105°=75°.
14.(10分)图1是一辆滑轮摄影轨道车,图2为其侧面示意图.DE⊥GH于点E,BC与CD是轨道车的“手臂”,可通过改变∠BCD的度数调节车的高度,在调节过程中,放摄像机的杆AB始终平行于DE.
(1)如图3所示,调节轨道车的“手臂”,使BC∥GH,此时∠BCD=25°,求∠CDE的度数.
(2)若图2中∠BCD=45°,求∠ABC与∠CDE的度数之和.
【解析】(1)如图1所示,过点C作CP∥AB,且点P在BC的下方.
因为DE⊥GH,AB∥DE,
所以AB⊥GH.
因为BC∥GH,所以AB⊥BC,
所以∠BCP=∠B=90°,所以∠DCP=∠BCP-∠BCD=90°-25°=65°.
因为AB∥DE,CP∥AB,所以CP∥DE,所以∠CDE=180°-∠DCP=180°-65°=115°.
(2)如图2所示,过点C作CP∥AB,且点P在BC的下方.
因为CP∥AB,所以∠ABC=∠BCP=∠BCD+∠DCP.
易知CP∥DE,所以∠CDE+∠DCP=180°.
因为∠DCP=∠ABC-∠BCD,
所以∠CDE+∠ABC-∠BCD=180°,所以∠CDE+∠ABC=180°+∠BCD=225°.
15.(10分)已知AD∥BC,AB∥CD,E在线段BC的延长线上,AE平分∠BAD,连接DE, ∠ADE=3∠CDE.
(1)若∠AED=60°,求∠CDE的度数.
(2)若∠AEB=60°,探究DE与BE的位置关系,并说明理由.
同课章节目录
