北师大版七年级数学下册期中素养评估课件

(共33张PPT)
综合学习评价
期中素养评估(第一、二章)
时间·120分钟 满分·120分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列运算中,错误的是( )
A.7m-3m=4m B.(-2m2)3=-8m6
C.(m-2)2=m2-2m+4 D.(m+1)(m-1)=m2-1
C
【解析】A.7m-3m=(7-3)m=4m,故正确,不符合题意;
B.(-2m2)3=(-2)3·(m2)3=-8m6,故正确,不符合题意;
C.(m-2)2=m2-4m+4,故不正确,符合题意;
D.(m+1)(m-1)=m2-1,故正确,不符合题意.
2.(2024·深圳龙华期中)1986年9月,深圳市评选簕杜鹃为深圳市市花,簕杜鹃又名三角
梅、九重葛.它的苞片大而美丽,颜色鲜艳,给人以奔放、热烈的感受.簕杜鹃的单粒
的花粉粒直径约为0.000 015 m,数据0.000 015用科学记数法表示为( )
A.1.5×10-5 B.1.5×10-6 C.15×10-6 D.15×10-7
A
【解析】0.000 015=1.5×10-5.
3.若(x+m)与(x+3)的乘积中不含x的一次项,则m的值为( )
A.-3 B.3 C.0 D.1
A
【解析】因为(x+m)(x+3)=x2+3x+mx+3m=x2+(3+m)x+3m,
又因为(x+m)与(x+3)的乘积中不含x的一次项,
所以3+m=0,
解得m=-3.
4.(2024·广东三模)潮州市的广济桥是中国古代著名桥梁之一,如图所示的照片是某
处栏杆的拐角,若AB∥DE,∠DEF=130°,CF⊥AC,则∠BAC的度数为( )
A.20° B.30° C.40° D.50°
C
【解析】因为AB∥DE,
所以∠ABF=∠DEF=130°.
所以∠ABC=180°-∠ABF=50°.
因为CF⊥AC,所以∠C=90°,
所以∠BAC=180°-∠C-∠ABC=40°.
5.(2024·揭阳惠来质检)已知6x3y5与一个多项式的积为24x3y7-18x5y5+12x7y6,则这个多
项式为( )
A.4y2-3x2　　B.4xy2-3x2y　　C.4y2-3x2+2x4y　　D.4y2-3x2+6x3y
C
【解析】因为6x3y5与一个多项式的积为24x3y7-18x5y5+12x7y6,
所以这个多项式为(24x3y7-18x5y5+12x7y6)÷6x3y5=4y2-3x2+2x4y.
6.(2024·广州天河质检)如图所示,直线AB,CD相交于点O,OE⊥OF.若∠1=80°,∠2=30°,
则∠3的度数为( )
A.30° B.40° C.50° D.60°
B
【解析】因为∠1=80°,
所以∠1=∠AOD=80°.
因为∠2=30°,
所以∠AOE=∠AOD-∠2=50°.
因为OE⊥OF,所以∠EOF=90°,
所以∠3=∠EOF-∠AOE=40°.
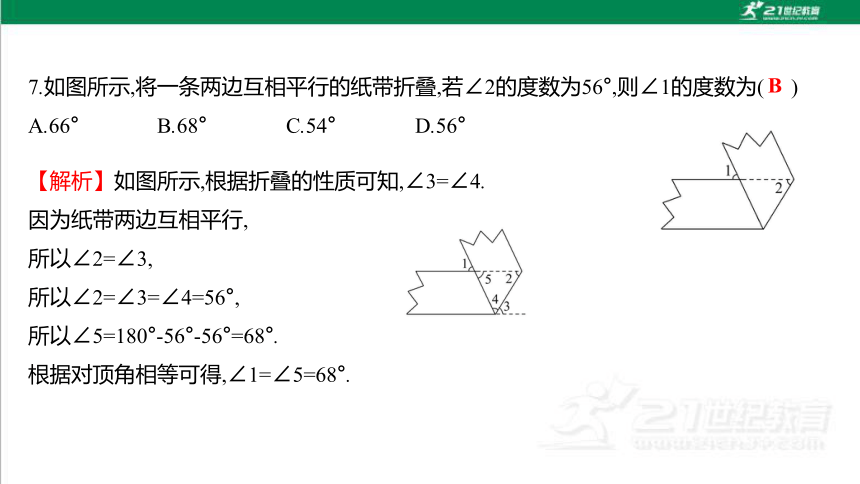
7.如图所示,将一条两边互相平行的纸带折叠,若∠2的度数为56°,则∠1的度数为( )
A.66° B.68° C.54° D.56°
B
【解析】如图所示,根据折叠的性质可知,∠3=∠4.
因为纸带两边互相平行,
所以∠2=∠3,
所以∠2=∠3=∠4=56°,
所以∠5=180°-56°-56°=68°.
根据对顶角相等可得,∠1=∠5=68°.
8.若某校把一个边长为a m的正方形花坛改建成长为(a+3)m,宽为(a-3)m的长方形花
坛,则长方形花坛与正方形花坛相比面积( )
A.没有变化 B.变大了 C.变小了 D.无法确定
C
【解析】边长为a m的正方形的面积为a2 m2,长为(a+3)m,宽为(a-3)m的长方形面积为(a+3)(a-3)=(a2-9)m2,
因为a2-(a2-9)=9(m2),
所以长方形花坛与正方形花坛相比面积减少了9 m2.
9.如图所示,两个正方形边长分别为a,b,若a+b=9,ab=12,则阴影部分的面积为( )
A.21.5 B.22.5 C.23.5 D.24
B
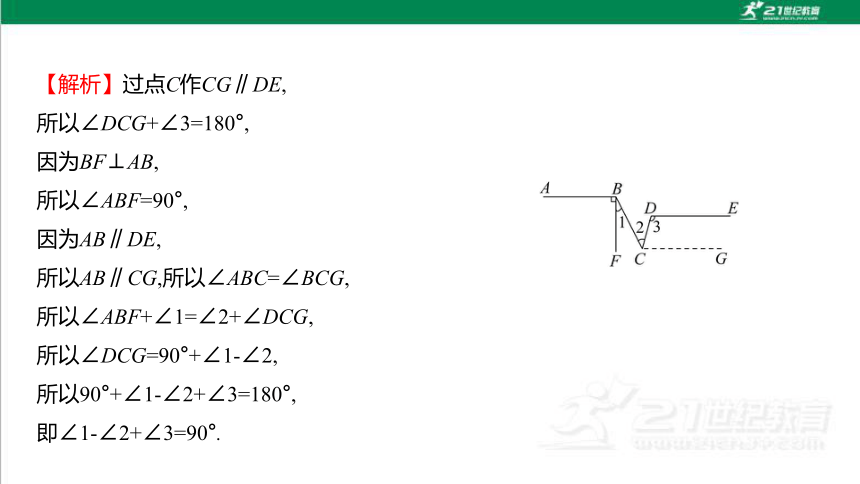
10.如图所示,如果AB∥DE,BF⊥AB,垂足为点B,那么∠1,∠2,∠3之间的数量关系
是( )
A.∠1+∠2+∠3=180° B.∠3-∠1+∠2=90°
C.∠3-∠1-∠2=90° D.∠3+∠1-∠2=90°
D
【解析】过点C作CG∥DE,
所以∠DCG+∠3=180°,
因为BF⊥AB,
所以∠ABF=90°,
因为AB∥DE,
所以AB∥CG,所以∠ABC=∠BCG,
所以∠ABF+∠1=∠2+∠DCG,
所以∠DCG=90°+∠1-∠2,
所以90°+∠1-∠2+∠3=180°,
即∠1-∠2+∠3=90°.
　36°　
12.长方形的面积为4a2-8ab+4a,若它的一边长为4a,则它的周长为_____________.
　10a-4b+2　
【解析】因为长方形的面积是4a2-8ab+4a,它的一边长为4a,
所以另一边长为(4a2-8ab+4a)÷4a=a-2b+1,
则它的周长是2(a-2b+1+4a)=10a-4b+2.
　6　
14.如图所示,若直线AB∥CD,AE⊥CE,∠1=126°,则∠C=_______°.
　36　
【解析】因为AE⊥CE,∠1=126°,
所以∠AEC=90°,∠BAE=180°-126°=54°.
如图所示,过E作EG∥AB,
因为AB∥CD,所以AB∥EG∥CD,
所以∠AEG=∠BAE=54°,∠C=∠CEG,
所以∠CEG=90°-54°=36°,
所以∠C=36°.
15.(2024·深圳罗湖期中)如图所示,直角三角形AOB和直角三角形COD中,∠AOB=
∠COD=90°,∠B=30°,∠C=45°,点D在边OA上,将图中的三角形COD绕点O按每秒15°
的速度沿顺时针方向旋转一周,在旋转的过程中,在第__________s时,边CD恰好与边
AB平行.
　5或17　
【解析】①两三角形在点O的同侧时,如图1所示,设CD与OA相交于点E.
因为∠AOB=90°,∠B=30°,
所以∠A=60°.
因为AB∥CD,
所以∠DEO=∠A=60°.
因为∠C=45°,∠COD=90°,
所以∠D=90°-45°=45°,
所以∠DOE=180°-60°-45°=75°.
因为每秒旋转15°,
所以时间为75°÷15°=5 s;
②两三角形在点O的异侧时,如图2所示,延长AO与CD相交于点E.
因为AB∥CD,
所以∠DEO=∠A=60°.
因为∠C=45°,∠COD=90°,
所以∠D=90°-45°=45°,
所以∠DOE=180°-60°-45°=75°,
所以旋转角为180°+75°=255°.
因为每秒旋转15°,
所以时间为255°÷15°=17 s.
综上所述,在第5或17 s时,边CD恰好与边AB平行.
18.(7分)小亮的一张地图上有A,B,C三个城市,但地图上的C城市被墨迹污染了(如图所示),但知道∠BAC=∠1,∠ABC=∠2,请你用尺规作图法帮他在图中确定C城市的具体位置.(用尺规作图,保留作图痕迹,不写作法)
【解析】如图所示,作∠EAB=∠1,∠FBA=∠2,射线AE交射线BF于点C,点C即为所求.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.(9分)(2024·茂名高州质检)为了纪念革命英雄夏明翰,衡阳市政府计划将一块长为(2a+b)m、宽为(a+b)m的长方形地块(如图所示)用于宣传革命英雄事迹,规划部门计划将阴影部分进行绿化,中间将修建一座夏明翰雕像.
(1)试用含a,b的代数式表示绿化的面积是多少平方米
(2)若a+b=5,ab=6,请求出绿化面积.
【解析】(1)根据题意,可得绿化的面积为(2a+b)(a+b)-a2=2a2+2ab+ab+b2-a2=(a2+3ab+b2)m2.
(2)因为a+b=5,ab=6,所以a2+3ab+b2=a2+2ab+b2+ab=(a+b)2+ab=52+6=31(m2).
20.(9分)如图所示,直线AB,BE相交于点B,直线CD,BE相交于点E,BE⊥DF于点P,连接CF,DF,∠1=∠C.
(1)若∠2=56°,请求出∠B的度数;
(2)若AB∥CD,求证:∠2+∠D=90°.
【解析】(1)因为∠1=∠C,所以BE∥CF,∠B=∠2=56°.
(2)因为BE⊥DF,所以∠DPE=90°,
因为BE∥CF,所以∠CFD=∠DPE=90°,
所以∠2+∠BFD=180°-∠CFD=90°,
因为AB∥CD,所以∠BFD=∠D,所以∠2+∠D=90°.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.(13分)如图所示,将一个边长为a的正方形图形分割成四部分(两个正方形和两个长方形),请认真观察图形,解答下列问题:
(1)请用两种方法表示该图形阴影部分的面积(用含a,b的代数式表示):
①方法一:　　　　　　　　　　;
②方法二:　　　　　　　　　　.
(2)若图中a,b满足a2+b2=31,ab=3,求阴影部分正方形的边长.
(3)若(2 021-y)(2 023-y)=1 010,求(2 021-y)2+(2 023-y)2的值.
【解析】(1)①题图中阴影部分的面积为(a-b)2;②题图中阴影部分的面积为a2-2ab+b2.
答案:①(a-b)2　② a2-2ab+b2
(2)(a-b)2=a2-2ab+b2=31-6=25,所以a-b=5(负值舍去).
答:阴影部分正方形的边长是5.
(3)设2 021-y=m,2 023-y=n,则mn=1 010,m-n=-2,
所以m2+n2=(m-n)2+2mn=(-2)2+2×1 010=4+2 020=2 024.
所以(2 021-y)2+(2 023-y)2=2 024.
23.(14分)如图所示,已知AB∥CD,AD∥BC,∠DCE=90°,点E在线段AB上,∠FCG=90°,点F在直线AD上,∠AHG=90°.
(1)找出图中与∠D相等的角,并说明理由;
(2)若∠ECF=25°,求∠BCD的度数;
(3)在(2)的条件下,点C(点C不与B,H两点重合)从点B出发,沿射线BG的方向运动,其他条件不变,求∠BAF的度数.
【解析】(1)与∠D相等的角为∠DCG,∠ECF,∠B,理由如下:因为AD∥BC,所以∠D=∠DCG,因为∠FCG=90°,∠DCE=90°,所以∠ECF=∠DCG,所以∠D=∠ECF,因为AB∥DC,所以∠DCG=∠B,所以∠B=∠D,所以与∠D相等的角为∠DCG,∠ECF,∠B.
(2)因为∠ECF=25°,∠DCE=90°,所以∠FCD=65°,
又因为∠BCF=90°,所以∠BCD=65°+90°=155°.
(3)如图所示,当点C在线段BH上时,点F在DA延长线上,
∠ECF=∠DCG=∠B=25°,因为AD∥BC,所以∠BAF=∠B=25°;
如图所示,当点C在BH延长线上时,点F在线段AD上,
因为∠B=25°,AD∥BC,所以∠BAF=180°-25°=155°.
综上所述,∠BAF的度数为25°或155°.