北师大版七年级数学下册期末素养评估课件
图片预览











文档简介
(共39张PPT)
期末素养评估(第一至第六章)
(时间· 120分钟 满分· 120分)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.“文化是一个国家、一个民族的灵魂.文化兴国运兴,文化强民族强.没有高度的文化
自信,没有文化的繁荣兴盛,就没有中华民族伟大复兴.”下列甲骨文中,可看作轴对称图
形的是( )
A
【解析】A.该图形是轴对称图形,符合题意;
B.该图形不是轴对称图形,不符合题意;
C.该图形不是轴对称图形,不符合题意;
D.该图形不是轴对称图形,不符合题意.
2.(2024·广州越秀一模)石墨烯堪称目前世界上最薄的材料,约为0.3 nm(1 nm=
0.000 000 001 m).与此同时,石墨烯比金刚石更硬,是世界上最坚硬又最薄的纳米材料.
0.3 nm用科学记数法可以表示为( )
A.3×10-8 m B.0.3×10-9 m C.3×10-9 m D.3×10-10 m
【解析】0.3 nm=0.3×0.000 000 001 m=3×10-10m .
D
3.(2024·深圳龙岗质检)若(x-1)(x-2)=x2+mx+n,则m+n的值为( )
A.-1 B.-5 C.5 D.1
【解析】因为(x-1)(x-2)=x2-3x+2,
所以m=-3,n=2,
所以m+n=-1.
A
4.(2024·揭阳普宁期末)用三根长度分别为4 cm,5 cm,10 cm的木条首尾顺次相接围成
三角形,这属于( )
A.不可能事件 B.随机事件 C.必然事件 D.不确定事件
【解析】因为4+5<10,所以三根长度分别为4 cm,5 cm,10 cm的木条不能围成三角形.
A
5.如图所示,在△ABC中,AB=AC,∠A=40°,则∠ACD的度数为( )
A.70° B.100°
C.110° D.140°
C
6.(2024·深圳光明质检)小聪上午8:00从家里出发,骑共享单车去一家超市购物,然后
从这家超市原路返回家中,小聪离家的路程y(m)和经过的时间x(min)之间的函数关系
如图所示,下列说法中,错误的是( )
A.从小聪家到超市的路程是1 800 m
B.小聪从家到超市的平均速度为180 m/min
C.小聪在超市购物用时35 min
D.小聪从超市返回家中的平均速度为26 m/min
D
【解析】A.观察题中图象发现:从小聪家到超市的路程是1 800 m,正确,不符合题意;
B.小聪去超市共用了10 min,行程1 800 m,平均速度为1 800÷10=180 m/min,正确,不符合题意;
C.小聪在超市购物用时45-10=35 min,正确,不符合题意;
D.(1 800-1 300)÷(50-45)=500÷5=100,所以小聪从超市返回家中的平均速度为100 m/min,错误,符合题意.
7.(2024·汕头金平区期中)如图所示,一个含有30°角的直角三角板的两个顶点放在一
个长方形的对边上,如果∠1=m°,那么用含m的式子表示∠2的度数是( )
A.(m+30)° B.(m+90)°
C.(m+120)° D.(150-m)°
【解析】如图所示,
∠BAC=180°-90°-∠1=90°-m°.
因为AB∥CD,所以∠BAC+∠2=180°,
所以90°-m°+∠2=180°,
所以∠2=(m+90)°.
B
8.如图所示,两个正方形的泳池,面积分别是S1和S2,两个泳池的面积之和S1+S2=20,点B
是线段CG上一点,设CG=6,在阴影部分铺上防滑瓷砖,则所需防滑瓷砖的面积为( )
A.5 B.4
C.8 D.10
B
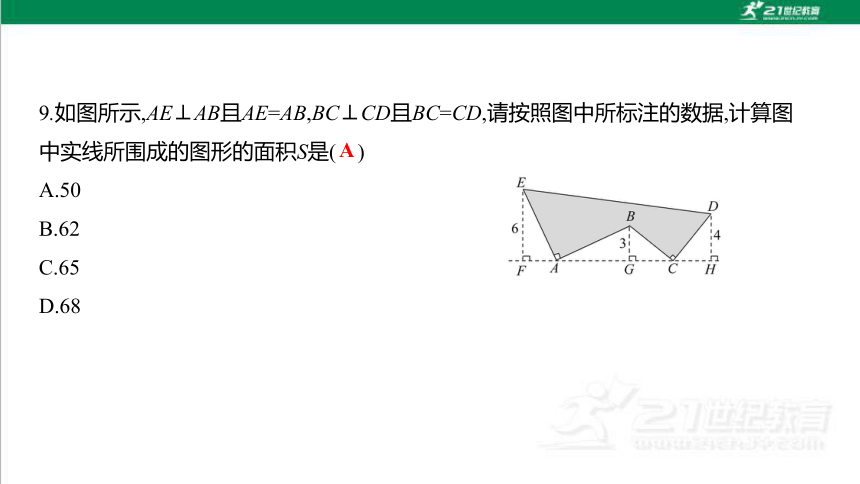
9.如图所示,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图
中实线所围成的图形的面积S是( )
A.50
B.62
C.65
D.68
A
D
二、填空题:本大题共5小题,每小题3分,共15分.
11.“彩缕碧筠粽,香粳白玉团.”端午佳节,小明妈妈准备了豆沙粽2个、红枣粽4个、腊
肉粽3个、蛋黄粽2个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概
率是_____.
12.(2024·深圳育才教育集团期末)一个角是它的补角的五分之一,则这个角的余角是
_______°.
60
13.(2024·东莞期末)如图所示,在△ABC中,∠ACB=97°,∠B=31°,点D在边AB上,将△BCD
沿CD折叠,点B落在B'处,若B'D∥AC,则∠BDC=_________.
116°
【解析】由作图过程可知,BP为∠ABC的平分线,
因为AD是边BC上的高,所以AD⊥BC,
因为MN⊥AB,所以MD=MN=2.
所以AD=4MD=8,
所以AM=AD-MD=6.
6
15.如图所示,牧童在A处放牛,其家在B处,A,B到河岸CD的距离分别为AC,BD,且AC=
BD,若A到河岸CD的中点的距离为500 m.牧童从A处把牛牵到河边饮水后再回家,牧
童回家所走的最短距离为____________.
1 000 m
18.(7分)如图所示,已知△ABC,点E是AB上一点.
(1)尺规作图:在BC上找到一点F,使得∠BFE=∠C;(不写作法,保留作图痕迹)
(2)在(1)的条件下,连接CE,若∠EFC=110°,且CE平分∠ACB,求∠FEC的度数.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.(9分)某校一课外小组准备进行“绿色环保”的宣传活动,需要制作宣传单,校园附近有一家印刷社,收费y(元)与印刷数量x(张)之间关系如表:
(1)表格反映了哪两个变量之间的关系
(2)直接写出收费y(元)与印刷数量x(张)之间的关系式;
(3)若收费为300元,求印刷宣传单的数量.
印刷数量x/张 … 100 200 300 400 …
收费y/元 … 15 30 45 60 …
【解析】(1)题表反映了印刷数量x和收费y两个变量之间的关系.
(2)由题表可知,印刷数量每增加100张,收费增加15元,所以每张的价格是0.15元.所以收费y(元)与印刷数量x(张)之间的关系式为y=0.15x.
(3)由(2)知y=0.15x,所以0.15x=300,
解得x=2 000,所以花费300元时,印了2 000张宣传单.
20.(9分)如图所示,在△ABC中,点D是边AB上一点,点E是边AC的中点,作CF∥AB交DE延长线于点F.
(1)试说明:△ADE≌△CFE;
(2)若∠ABC=∠ACB,CE=3,CF=4,求DB的长.
21.(9分)如图所示,现有一个可以自由转动的转盘(转盘被等分成8个扇形),每个扇形区域内分别标有1,2,3,4,5,6,7,8这八个数字,转动转盘,停止转动后,指针指向的数字即为转出的数字,请回答下列问题:
(1)转出的数字为1是 ,转出的数字为9是 ;
(从“随机事件”“必然事件”“不可能事件”中选一个填空)
(2)转动转盘,转出的数字是奇数的概率是 ;
(3)现有两张分别写有2和5的卡片,随机转动转盘,转盘停止转动后,记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.这三条线段能构成三角形的概率是 .
(2)①由题图2可知,大正方体的体积可表示为(a+b)3.
大正方体的体积还可表示为八个小长方体的体积之和:a3+a2b+a2b+ab2+a2b+ab2+ab2+b3=a3+3a2b+3ab2+b3,所以(a+b)3=a3+3a2b+3ab2+b3.
答案:a3+3a2b+3ab2+b3
②因为a+b=6,ab=7,
所以a3+b3=(a+b)3-3a2b-3ab2=(a+b)3-3ab(a+b)=63-3×7×6=90,
故a3+b3=90.
23.(14分)【问题提出】小颖同学在学习中自主探究以下问题,请你解答她提出的问题:
(1)如图1所示,已知AB∥CD,点E为AB,CD之间一点,连接BE,DE,得到∠BED.请猜想∠BED与∠B,∠D之间的数量关系,并证明;
(2)如图2所示,已知AB∥CD,点E为AB,CD之间一点,∠ABE和∠CDE的平分线相交于点F,若∠E=80°,求∠F的度数.
【类比迁移】小颖结合角平分线的知识将问题进行深入探究,如图3所示,已知:AB∥CD,点E的位置移到AB上方,点F在EB延长线上,且BG平分∠ABF与∠CDE的平分线DG相交于点G,请直接写出∠G与∠E之间的数量关系 .
【变式挑战】小颖在本次探究的最后将条件AB∥CD去掉,提出了以下问题:
已知AB与CD不平行,如图4所示,点M在AB上,点N在CD上,连接MN,且MN同时平分∠BME和∠DNE,请直接写出∠AME,∠CNE,∠MEN之间的数量关系 .
【解析】【问题提出】(1)猜想:∠BED=∠D+∠B,
证明:如图1所示,过点E作EF∥AB,
因为AB∥CD,所以AB∥CD∥EF,所以∠ABE=∠BEF,∠CDE=∠DEF,
所以∠BED=∠D+∠B.
(2)如图2所示,作EG∥AB,FH∥AB,
因为AB∥CD,所以EG∥AB∥FH∥CD,
所以∠ABF=∠BFH,∠CDF=∠DFH,∠ABE+∠BEG=180°,∠GED+∠CDE=180°,所以∠ABE+∠BEG+∠GED+∠CDE=360°,
【变式挑战】2∠MEN=∠AME+∠CNE,理由如下:
如图4所示,延长AB,CD,交于点P,
过M作射线MF,过E作EG∥MF,过P作PH∥MF,过N作NK∥MF,
所以MF∥EG∥NK∥HP,∠AMF=∠APH,∠CNK=∠CPH,所以∠MPN=∠CPH+∠APH=∠CNK+∠AMF,同理得∠MEN=∠FME+∠KNE,
所以∠MPN+∠MEN=∠FME+∠KNE+∠CNK+∠AMF=∠AME+∠CNE,
因为MN同时平分∠BME和∠DNE,
所以∠EMN=∠PMN,∠ENM=∠MNP,
所以∠MEN=∠MPN,即2∠MEN=∠AME+∠CNE.
答案:2∠MEN=∠AME+∠CNE
期末素养评估(第一至第六章)
(时间· 120分钟 满分· 120分)
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.“文化是一个国家、一个民族的灵魂.文化兴国运兴,文化强民族强.没有高度的文化
自信,没有文化的繁荣兴盛,就没有中华民族伟大复兴.”下列甲骨文中,可看作轴对称图
形的是( )
A
【解析】A.该图形是轴对称图形,符合题意;
B.该图形不是轴对称图形,不符合题意;
C.该图形不是轴对称图形,不符合题意;
D.该图形不是轴对称图形,不符合题意.
2.(2024·广州越秀一模)石墨烯堪称目前世界上最薄的材料,约为0.3 nm(1 nm=
0.000 000 001 m).与此同时,石墨烯比金刚石更硬,是世界上最坚硬又最薄的纳米材料.
0.3 nm用科学记数法可以表示为( )
A.3×10-8 m B.0.3×10-9 m C.3×10-9 m D.3×10-10 m
【解析】0.3 nm=0.3×0.000 000 001 m=3×10-10m .
D
3.(2024·深圳龙岗质检)若(x-1)(x-2)=x2+mx+n,则m+n的值为( )
A.-1 B.-5 C.5 D.1
【解析】因为(x-1)(x-2)=x2-3x+2,
所以m=-3,n=2,
所以m+n=-1.
A
4.(2024·揭阳普宁期末)用三根长度分别为4 cm,5 cm,10 cm的木条首尾顺次相接围成
三角形,这属于( )
A.不可能事件 B.随机事件 C.必然事件 D.不确定事件
【解析】因为4+5<10,所以三根长度分别为4 cm,5 cm,10 cm的木条不能围成三角形.
A
5.如图所示,在△ABC中,AB=AC,∠A=40°,则∠ACD的度数为( )
A.70° B.100°
C.110° D.140°
C
6.(2024·深圳光明质检)小聪上午8:00从家里出发,骑共享单车去一家超市购物,然后
从这家超市原路返回家中,小聪离家的路程y(m)和经过的时间x(min)之间的函数关系
如图所示,下列说法中,错误的是( )
A.从小聪家到超市的路程是1 800 m
B.小聪从家到超市的平均速度为180 m/min
C.小聪在超市购物用时35 min
D.小聪从超市返回家中的平均速度为26 m/min
D
【解析】A.观察题中图象发现:从小聪家到超市的路程是1 800 m,正确,不符合题意;
B.小聪去超市共用了10 min,行程1 800 m,平均速度为1 800÷10=180 m/min,正确,不符合题意;
C.小聪在超市购物用时45-10=35 min,正确,不符合题意;
D.(1 800-1 300)÷(50-45)=500÷5=100,所以小聪从超市返回家中的平均速度为100 m/min,错误,符合题意.
7.(2024·汕头金平区期中)如图所示,一个含有30°角的直角三角板的两个顶点放在一
个长方形的对边上,如果∠1=m°,那么用含m的式子表示∠2的度数是( )
A.(m+30)° B.(m+90)°
C.(m+120)° D.(150-m)°
【解析】如图所示,
∠BAC=180°-90°-∠1=90°-m°.
因为AB∥CD,所以∠BAC+∠2=180°,
所以90°-m°+∠2=180°,
所以∠2=(m+90)°.
B
8.如图所示,两个正方形的泳池,面积分别是S1和S2,两个泳池的面积之和S1+S2=20,点B
是线段CG上一点,设CG=6,在阴影部分铺上防滑瓷砖,则所需防滑瓷砖的面积为( )
A.5 B.4
C.8 D.10
B
9.如图所示,AE⊥AB且AE=AB,BC⊥CD且BC=CD,请按照图中所标注的数据,计算图
中实线所围成的图形的面积S是( )
A.50
B.62
C.65
D.68
A
D
二、填空题:本大题共5小题,每小题3分,共15分.
11.“彩缕碧筠粽,香粳白玉团.”端午佳节,小明妈妈准备了豆沙粽2个、红枣粽4个、腊
肉粽3个、蛋黄粽2个,其中豆沙粽和红枣粽是甜粽.小明任意选取一个,选到甜粽的概
率是_____.
12.(2024·深圳育才教育集团期末)一个角是它的补角的五分之一,则这个角的余角是
_______°.
60
13.(2024·东莞期末)如图所示,在△ABC中,∠ACB=97°,∠B=31°,点D在边AB上,将△BCD
沿CD折叠,点B落在B'处,若B'D∥AC,则∠BDC=_________.
116°
【解析】由作图过程可知,BP为∠ABC的平分线,
因为AD是边BC上的高,所以AD⊥BC,
因为MN⊥AB,所以MD=MN=2.
所以AD=4MD=8,
所以AM=AD-MD=6.
6
15.如图所示,牧童在A处放牛,其家在B处,A,B到河岸CD的距离分别为AC,BD,且AC=
BD,若A到河岸CD的中点的距离为500 m.牧童从A处把牛牵到河边饮水后再回家,牧
童回家所走的最短距离为____________.
1 000 m
18.(7分)如图所示,已知△ABC,点E是AB上一点.
(1)尺规作图:在BC上找到一点F,使得∠BFE=∠C;(不写作法,保留作图痕迹)
(2)在(1)的条件下,连接CE,若∠EFC=110°,且CE平分∠ACB,求∠FEC的度数.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.(9分)某校一课外小组准备进行“绿色环保”的宣传活动,需要制作宣传单,校园附近有一家印刷社,收费y(元)与印刷数量x(张)之间关系如表:
(1)表格反映了哪两个变量之间的关系
(2)直接写出收费y(元)与印刷数量x(张)之间的关系式;
(3)若收费为300元,求印刷宣传单的数量.
印刷数量x/张 … 100 200 300 400 …
收费y/元 … 15 30 45 60 …
【解析】(1)题表反映了印刷数量x和收费y两个变量之间的关系.
(2)由题表可知,印刷数量每增加100张,收费增加15元,所以每张的价格是0.15元.所以收费y(元)与印刷数量x(张)之间的关系式为y=0.15x.
(3)由(2)知y=0.15x,所以0.15x=300,
解得x=2 000,所以花费300元时,印了2 000张宣传单.
20.(9分)如图所示,在△ABC中,点D是边AB上一点,点E是边AC的中点,作CF∥AB交DE延长线于点F.
(1)试说明:△ADE≌△CFE;
(2)若∠ABC=∠ACB,CE=3,CF=4,求DB的长.
21.(9分)如图所示,现有一个可以自由转动的转盘(转盘被等分成8个扇形),每个扇形区域内分别标有1,2,3,4,5,6,7,8这八个数字,转动转盘,停止转动后,指针指向的数字即为转出的数字,请回答下列问题:
(1)转出的数字为1是 ,转出的数字为9是 ;
(从“随机事件”“必然事件”“不可能事件”中选一个填空)
(2)转动转盘,转出的数字是奇数的概率是 ;
(3)现有两张分别写有2和5的卡片,随机转动转盘,转盘停止转动后,记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.这三条线段能构成三角形的概率是 .
(2)①由题图2可知,大正方体的体积可表示为(a+b)3.
大正方体的体积还可表示为八个小长方体的体积之和:a3+a2b+a2b+ab2+a2b+ab2+ab2+b3=a3+3a2b+3ab2+b3,所以(a+b)3=a3+3a2b+3ab2+b3.
答案:a3+3a2b+3ab2+b3
②因为a+b=6,ab=7,
所以a3+b3=(a+b)3-3a2b-3ab2=(a+b)3-3ab(a+b)=63-3×7×6=90,
故a3+b3=90.
23.(14分)【问题提出】小颖同学在学习中自主探究以下问题,请你解答她提出的问题:
(1)如图1所示,已知AB∥CD,点E为AB,CD之间一点,连接BE,DE,得到∠BED.请猜想∠BED与∠B,∠D之间的数量关系,并证明;
(2)如图2所示,已知AB∥CD,点E为AB,CD之间一点,∠ABE和∠CDE的平分线相交于点F,若∠E=80°,求∠F的度数.
【类比迁移】小颖结合角平分线的知识将问题进行深入探究,如图3所示,已知:AB∥CD,点E的位置移到AB上方,点F在EB延长线上,且BG平分∠ABF与∠CDE的平分线DG相交于点G,请直接写出∠G与∠E之间的数量关系 .
【变式挑战】小颖在本次探究的最后将条件AB∥CD去掉,提出了以下问题:
已知AB与CD不平行,如图4所示,点M在AB上,点N在CD上,连接MN,且MN同时平分∠BME和∠DNE,请直接写出∠AME,∠CNE,∠MEN之间的数量关系 .
【解析】【问题提出】(1)猜想:∠BED=∠D+∠B,
证明:如图1所示,过点E作EF∥AB,
因为AB∥CD,所以AB∥CD∥EF,所以∠ABE=∠BEF,∠CDE=∠DEF,
所以∠BED=∠D+∠B.
(2)如图2所示,作EG∥AB,FH∥AB,
因为AB∥CD,所以EG∥AB∥FH∥CD,
所以∠ABF=∠BFH,∠CDF=∠DFH,∠ABE+∠BEG=180°,∠GED+∠CDE=180°,所以∠ABE+∠BEG+∠GED+∠CDE=360°,
【变式挑战】2∠MEN=∠AME+∠CNE,理由如下:
如图4所示,延长AB,CD,交于点P,
过M作射线MF,过E作EG∥MF,过P作PH∥MF,过N作NK∥MF,
所以MF∥EG∥NK∥HP,∠AMF=∠APH,∠CNK=∠CPH,所以∠MPN=∠CPH+∠APH=∠CNK+∠AMF,同理得∠MEN=∠FME+∠KNE,
所以∠MPN+∠MEN=∠FME+∠KNE+∠CNK+∠AMF=∠AME+∠CNE,
因为MN同时平分∠BME和∠DNE,
所以∠EMN=∠PMN,∠ENM=∠MNP,
所以∠MEN=∠MPN,即2∠MEN=∠AME+∠CNE.
答案:2∠MEN=∠AME+∠CNE
同课章节目录
