中考数学复习第二章方程(组)与不等式(组)第二节一元二次方程及其应用课件
文档属性
| 名称 | 中考数学复习第二章方程(组)与不等式(组)第二节一元二次方程及其应用课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:16:00 | ||
图片预览






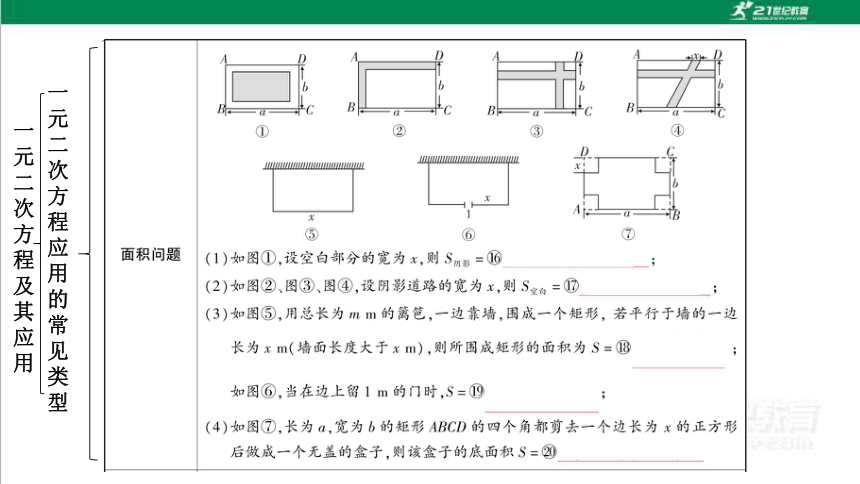





文档简介
(共38张PPT)
一元二次方程及其应用
一元二次方程
一元二次方程及其应用
一元二次方程的解法
一元二次方程及其应用
一元二次方程及其应用
一元二次方程应用的常见类型
一元二次方程及其应用
一元二次方程应用的常见类型
一元二次方程及其应用
一元二次方程应用的常见类型
一元二次方程及其应用
一元二次方程应用的常见类型
一元二次方程及其应用
一元二次方程应用的常见类型
1.某品牌新能源汽车2021年的销售量为20万辆,随着消费人群的不断增多,该品牌新能源汽车的销售量逐年递增,2023年的销售量比2021年增加了31.2万辆.如果设从2021年到2023年该品牌新能源汽车销售量的平均年增长率为x,那么可列方程为 .
【变式】某市一共有285个社区,计划三个季度全部实现垃圾分类,第一季度已有60个社区实现垃圾分类,预计第二、三季度实现垃圾分类的社区个数较前一季度平均增长率均为x,则可列方程为 .
20(1+x)2-20=31.2
60+60(1+x)+60(1+x)2=285
2.某种服装平均每天可销售20件,每件盈利44元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售5件,如果每天要盈利1 600 元,每件降价多少元?设每件降价x元,则可列方程为 .
(44-x)(20+5x)=1 600
3.如图,公园原有一块正方形空地,后来从这块空地上划出部分区域栽种鲜花(阴影部分),原空地一边减少了3 m,另一边减少了2 m,剩余空地面积为56
m2,设正方形空地原来的边长为x m,则可列方程为 .
(x-2)(x-3)=56
4.我校八年级组织班级篮球赛,赛制为单循环形式(即每两班之间都比赛一场),若共进行了45场比赛,则有 个班级篮球队参加.
5.现有一个人因支原体感染,感冒发热,经过两轮传染后共有169人被感染,则每轮传染中平均一个人传染的人数是 人.
10
12
6.(1)方程2(x-3)2-18=0的解为 ;
(2)方程2x2+x-2=0的解为 ;
(3)方程x2+2x-3=0的解为 ;
(4)方程2x(x-2)=2-x的解为 .
x1=6,x2=0
x1=-3,x2=1
7.已知x1,x2是一元二次方程x2-6x+8=0的两根,则x1+x2-x1x2= .
8.(1)已知关于x的一元二次方程(a-2)x2+x+a2-4=0的一个根是0,则a的值为 ;
(2)若m是方程2x2-3x+1=0的一个根,则6m2-9m+2 025= .
9.一元二次方程mx2+2x+1=0有实数根,则m的取值范围是 .
-2
-2
2 022
m≤1且m≠0
重难点1:一元二次方程根的判别式及根与系数的关系
[一题多角度]已知关于x的一元二次方程x2-4x+5-a=0.
(1)若此方程没有实数根,则a的取值范围为 ;
(2)若此方程有两个不等的实数根,则a的取值范围为 ;
(3)若此方程有两个相等的实数根,则a的取值范围为 ;
(4)若此方程有一个根为3,则a的值为 ,方程的另一个根为 ;
(5)若此方程有两个实数根x1,x2,且(x1+1)(x2+1)=8,则a的值为 ;
(6)若y=x2-4x+5-a向下平移2个单位长度后与y=3恰好只有一个交点,则a的值为 .
a<1
a>1
a=1
2
1
2
-4
重难点2:一元二次方程的应用
[一题多角度]做好经济工作,推动经济稳定健康发展是我国当前的重要任务.新兴AI人工智能产业具有重要经济属性,各种智能大模型陆续涌现.
(1)银川市一家AI初创公司准备用24 m长的隔离板围成一面靠墙(墙长12 m),大小相等且彼此相连的三个矩形办公场地(如图),场地的面积能够达到32 m2吗?若能,给出方案;若不能,请说明理由;
解:能.理由:设垂直于墙的一边长x m,则平行于墙的一边长为(24-4x)m,且24-4x≤12,即x≥3.根据题意有(24-4x)x=32,解得x1=4,x2=2(舍去),
故垂直于墙的一边长为4 m,平行于墙的一边长为8 m.
【分层分析】设垂直于墙的一边长x m,再用含x的代数式表示出场地的另一边长为(24-4x)m,根据面积列出方程,再解方程即可,能否达到要求,根据解方程的结果,结合实际情况作出判断.
(2)该AI公司推出了一款智能学习电子设备.为了加快市场占有率,公司决定对该款产品进行降价促销,根据市场调查:这种电子设备销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个电子设备的固定成本为100元,则这种电子设备降价后的销售单价为多少时,公司每天可获利32 000元?
解:设降价后的单价为x元,则每天可售出[300+5(200-x)]个,依题意得(x-100)[300+5(200-x)]=32 000,
整理得x2-360x+32 400=0,解得x1=x2=180.
180<200,符合题意.
答:这种电子设备降价后的销售单价为180元时,公司每天可获利32 000元.
【分层分析】设降价后的销售单价为x元,则降价后每天可售出[300+5(200-x)]个,根据总利润=每个产品的利润×销售数量,即可得出关于x的一元二次方程,解之即可得出结论,注意结果是否符合实际.
解题绿色通道——十字相乘法解一元二次方程
【方法归纳】(注意运用十字相乘法易出现符号错误,要用根与系数关系验证)
使用一个十字叉来因式分解的方法叫做十字相乘法.如:
【方法应用】
解下列一元二方程:
(1)x2-7x-8=0; (2)x2+6x+8=0;
(3)2x2+5x-3=0; (4)6x2+64x-70=0.
解:(1)因式分解得(x-8)(x+1)=0,
∴x1=8,x2=-1.
(2)因式分解得(x+2)(x+4)=0,
∴x1=-2,x2=-4.
【考情分析】宁夏近五年主要考查用一元二次方程根的判别式求字母系数的取值范围;一元二次方程的简单实际应用等.
命题点1:一元二次方程根的判别式(近5年考查2次)
1.(2021·宁夏第5题3分)关于x的一元二次方程x2-2x+m-1=0有两个不等的实数根,则实数m的取值范围是 ( )
A.m≥2 B.m≤2
C.m>2 D.m<2
2.(2023·宁夏第11题3分)方程x2-4x-m=0有两个相等的实数根,则
m的值为 .
D
-4
命题点2:一元二次方程的实际应用(近5年考查1次)
3.(2022·宁夏第6题3分)受国际油价影响,今年我国汽油价格总体呈上升趋势.某地92号汽油价格三月底是6.2元/L,五月底是8.9元/L.设该地92号汽油价格这两个月平均每月的增长率为x,下列方程,正确的是( )
A.6.2(1+x)2=8.9
B.8.9(1+x)2=6.2
C.6.2(1+x2)=8.9
D.6.2(1+x)+6.2(1+x)2=8.9
A
C
5.(2024·潍坊)已知关于x的一元二次方程x2-mx-n2+mn+1=0,其中m,n满足m-2n=3,关于该方程根的情况,下列判断中正确的是( )
A.无实数根
B.有两个相等的实数根
C.有两个不等的实数根
D.无法确定
C
6.(2024·青海)
(1)解一元二次方程:x2-4x+3=0;
解:(1)x2-4x+3=0,
∴(x-1)(x-3)=0,
∴x-1=0或x-3=0,
∴x1=1,x2=3.
(2)若直角三角形的两边长分别是(1)中方程的根,求第三边的长.
7.(2024·南充)已知x1,x2是关于x的方程x2-2kx+k2-k+1=0的两个不等的实数根.
(1)k的取值范围为 ;
(2)若k<5,且k,x1,x2都是整数,求k的值.
k>1
解:(2)∵1<k<5,∴整数k的值为2,3,4,
当k=2时,方程为 x2-4x+3=0,
解得x1=1,x2=3,
当k=3或4时,此时方程的解不为整数.
综上所述,k的值为2.
一元二次方程及其应用
一元二次方程
一元二次方程及其应用
一元二次方程的解法
一元二次方程及其应用
一元二次方程及其应用
一元二次方程应用的常见类型
一元二次方程及其应用
一元二次方程应用的常见类型
一元二次方程及其应用
一元二次方程应用的常见类型
一元二次方程及其应用
一元二次方程应用的常见类型
一元二次方程及其应用
一元二次方程应用的常见类型
1.某品牌新能源汽车2021年的销售量为20万辆,随着消费人群的不断增多,该品牌新能源汽车的销售量逐年递增,2023年的销售量比2021年增加了31.2万辆.如果设从2021年到2023年该品牌新能源汽车销售量的平均年增长率为x,那么可列方程为 .
【变式】某市一共有285个社区,计划三个季度全部实现垃圾分类,第一季度已有60个社区实现垃圾分类,预计第二、三季度实现垃圾分类的社区个数较前一季度平均增长率均为x,则可列方程为 .
20(1+x)2-20=31.2
60+60(1+x)+60(1+x)2=285
2.某种服装平均每天可销售20件,每件盈利44元,在每件降价幅度不超过10元的情况下,若每件降价1元,则每天可多售5件,如果每天要盈利1 600 元,每件降价多少元?设每件降价x元,则可列方程为 .
(44-x)(20+5x)=1 600
3.如图,公园原有一块正方形空地,后来从这块空地上划出部分区域栽种鲜花(阴影部分),原空地一边减少了3 m,另一边减少了2 m,剩余空地面积为56
m2,设正方形空地原来的边长为x m,则可列方程为 .
(x-2)(x-3)=56
4.我校八年级组织班级篮球赛,赛制为单循环形式(即每两班之间都比赛一场),若共进行了45场比赛,则有 个班级篮球队参加.
5.现有一个人因支原体感染,感冒发热,经过两轮传染后共有169人被感染,则每轮传染中平均一个人传染的人数是 人.
10
12
6.(1)方程2(x-3)2-18=0的解为 ;
(2)方程2x2+x-2=0的解为 ;
(3)方程x2+2x-3=0的解为 ;
(4)方程2x(x-2)=2-x的解为 .
x1=6,x2=0
x1=-3,x2=1
7.已知x1,x2是一元二次方程x2-6x+8=0的两根,则x1+x2-x1x2= .
8.(1)已知关于x的一元二次方程(a-2)x2+x+a2-4=0的一个根是0,则a的值为 ;
(2)若m是方程2x2-3x+1=0的一个根,则6m2-9m+2 025= .
9.一元二次方程mx2+2x+1=0有实数根,则m的取值范围是 .
-2
-2
2 022
m≤1且m≠0
重难点1:一元二次方程根的判别式及根与系数的关系
[一题多角度]已知关于x的一元二次方程x2-4x+5-a=0.
(1)若此方程没有实数根,则a的取值范围为 ;
(2)若此方程有两个不等的实数根,则a的取值范围为 ;
(3)若此方程有两个相等的实数根,则a的取值范围为 ;
(4)若此方程有一个根为3,则a的值为 ,方程的另一个根为 ;
(5)若此方程有两个实数根x1,x2,且(x1+1)(x2+1)=8,则a的值为 ;
(6)若y=x2-4x+5-a向下平移2个单位长度后与y=3恰好只有一个交点,则a的值为 .
a<1
a>1
a=1
2
1
2
-4
重难点2:一元二次方程的应用
[一题多角度]做好经济工作,推动经济稳定健康发展是我国当前的重要任务.新兴AI人工智能产业具有重要经济属性,各种智能大模型陆续涌现.
(1)银川市一家AI初创公司准备用24 m长的隔离板围成一面靠墙(墙长12 m),大小相等且彼此相连的三个矩形办公场地(如图),场地的面积能够达到32 m2吗?若能,给出方案;若不能,请说明理由;
解:能.理由:设垂直于墙的一边长x m,则平行于墙的一边长为(24-4x)m,且24-4x≤12,即x≥3.根据题意有(24-4x)x=32,解得x1=4,x2=2(舍去),
故垂直于墙的一边长为4 m,平行于墙的一边长为8 m.
【分层分析】设垂直于墙的一边长x m,再用含x的代数式表示出场地的另一边长为(24-4x)m,根据面积列出方程,再解方程即可,能否达到要求,根据解方程的结果,结合实际情况作出判断.
(2)该AI公司推出了一款智能学习电子设备.为了加快市场占有率,公司决定对该款产品进行降价促销,根据市场调查:这种电子设备销售单价定为200元时,每天可售出300个;若销售单价每降低1元,每天可多售出5个.已知每个电子设备的固定成本为100元,则这种电子设备降价后的销售单价为多少时,公司每天可获利32 000元?
解:设降价后的单价为x元,则每天可售出[300+5(200-x)]个,依题意得(x-100)[300+5(200-x)]=32 000,
整理得x2-360x+32 400=0,解得x1=x2=180.
180<200,符合题意.
答:这种电子设备降价后的销售单价为180元时,公司每天可获利32 000元.
【分层分析】设降价后的销售单价为x元,则降价后每天可售出[300+5(200-x)]个,根据总利润=每个产品的利润×销售数量,即可得出关于x的一元二次方程,解之即可得出结论,注意结果是否符合实际.
解题绿色通道——十字相乘法解一元二次方程
【方法归纳】(注意运用十字相乘法易出现符号错误,要用根与系数关系验证)
使用一个十字叉来因式分解的方法叫做十字相乘法.如:
【方法应用】
解下列一元二方程:
(1)x2-7x-8=0; (2)x2+6x+8=0;
(3)2x2+5x-3=0; (4)6x2+64x-70=0.
解:(1)因式分解得(x-8)(x+1)=0,
∴x1=8,x2=-1.
(2)因式分解得(x+2)(x+4)=0,
∴x1=-2,x2=-4.
【考情分析】宁夏近五年主要考查用一元二次方程根的判别式求字母系数的取值范围;一元二次方程的简单实际应用等.
命题点1:一元二次方程根的判别式(近5年考查2次)
1.(2021·宁夏第5题3分)关于x的一元二次方程x2-2x+m-1=0有两个不等的实数根,则实数m的取值范围是 ( )
A.m≥2 B.m≤2
C.m>2 D.m<2
2.(2023·宁夏第11题3分)方程x2-4x-m=0有两个相等的实数根,则
m的值为 .
D
-4
命题点2:一元二次方程的实际应用(近5年考查1次)
3.(2022·宁夏第6题3分)受国际油价影响,今年我国汽油价格总体呈上升趋势.某地92号汽油价格三月底是6.2元/L,五月底是8.9元/L.设该地92号汽油价格这两个月平均每月的增长率为x,下列方程,正确的是( )
A.6.2(1+x)2=8.9
B.8.9(1+x)2=6.2
C.6.2(1+x2)=8.9
D.6.2(1+x)+6.2(1+x)2=8.9
A
C
5.(2024·潍坊)已知关于x的一元二次方程x2-mx-n2+mn+1=0,其中m,n满足m-2n=3,关于该方程根的情况,下列判断中正确的是( )
A.无实数根
B.有两个相等的实数根
C.有两个不等的实数根
D.无法确定
C
6.(2024·青海)
(1)解一元二次方程:x2-4x+3=0;
解:(1)x2-4x+3=0,
∴(x-1)(x-3)=0,
∴x-1=0或x-3=0,
∴x1=1,x2=3.
(2)若直角三角形的两边长分别是(1)中方程的根,求第三边的长.
7.(2024·南充)已知x1,x2是关于x的方程x2-2kx+k2-k+1=0的两个不等的实数根.
(1)k的取值范围为 ;
(2)若k<5,且k,x1,x2都是整数,求k的值.
k>1
解:(2)∵1<k<5,∴整数k的值为2,3,4,
当k=2时,方程为 x2-4x+3=0,
解得x1=1,x2=3,
当k=3或4时,此时方程的解不为整数.
综上所述,k的值为2.
同课章节目录
