中考数学复习第六章圆第二节与圆有关的位置关系课件
文档属性
| 名称 | 中考数学复习第六章圆第二节与圆有关的位置关系课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:16:00 | ||
图片预览









文档简介
(共53张PPT)
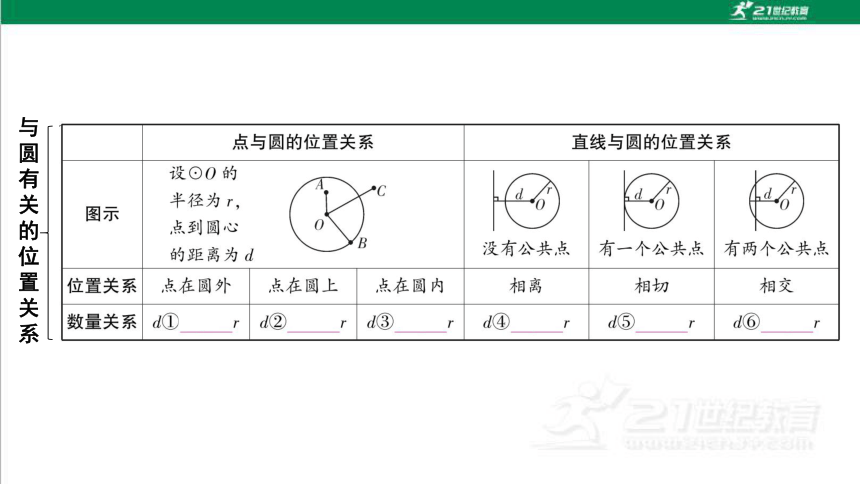
与圆有关的位置关系
与圆有关的位置关系
与圆有关的位置关系
与圆有关的位置关系
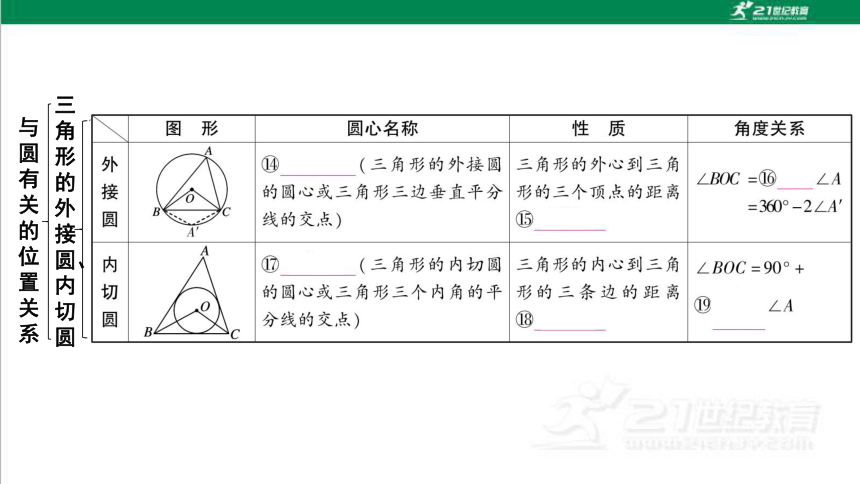
三角形的外接圆、内切圆
与圆有关的位置关系
三角形的外接圆、内切圆
与圆有关的位置关系
1.如果直径为13 cm的圆与一条直线有两个公共点,则圆心到该直线的距离d满足( )
A.d=13 cm
B.d=6.5 cm
C.0 cm≤d<6.5 cm
D.d>6.5 cm
C
B
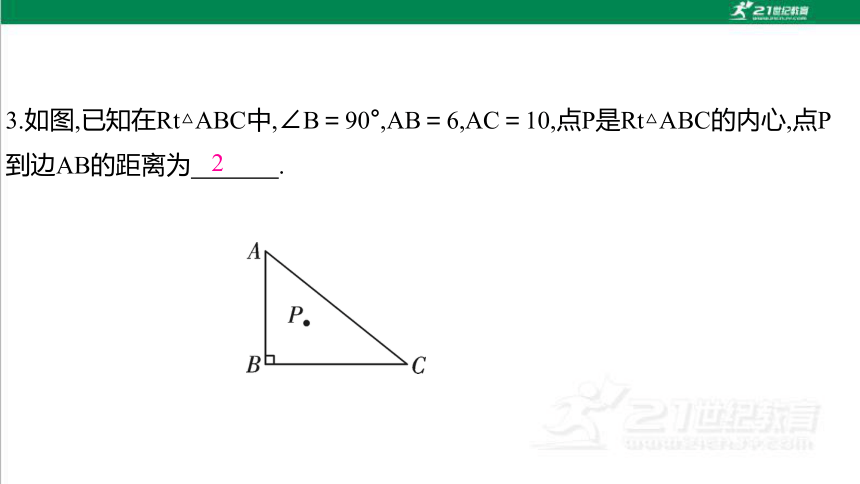
3.如图,已知在Rt△ABC中,∠B=90°,AB=6,AC=10,点P是Rt△ABC的内心,点P到边AB的距离为 .
2
4.如图,在平面直角坐标系xOy中,点A(0,3),点B(2,1),点C(2,-3).则经画图操作可知:△ABC的外接圆的圆心坐标是 .
(-2,-1)
5.如图,AD切⊙O于点A,AB是⊙O的直径,BD交⊙O于点C.已知AD=2,AB=4,则弦BC的长为 .
6.如图,PA,PB是⊙O的两条切线,A,B是切点,若∠APB=60°,则∠OPB= .
30°
7.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.连接BD,若∠C=50°,则∠DBE= .
65°
重难点:与切线相关的证明与计算
突破设问一 切线的判定
考向1:切点确定,连半径,证垂直
(1)如图①,AB是⊙O的直径,AB=AC,点D在⊙O上,DE⊥AC于点E.求证:DE是⊙O的切线;
证明:连接OD,
∵OB=OD,∴∠B=∠1,
∵AB=AC,∴∠B=∠C,
∴∠1=∠C,∴OD∥AC,
∵DE⊥AC,∴OD⊥DE,
又∵点D在⊙O上,∴DE是⊙O的切线.
(2)如图②,AB是⊙O的直径,AD平分∠CAB,点D在⊙O上,CD⊥AC于点C.求证:CD是⊙O的切线;
证明:连接OD,
∵AD平分∠CAB,
∴∠CAD=∠BAD.
又∵OD=OA,∴∠BAD=∠ADO,
∴∠ADO=∠CAD,∴AC∥OD,
∵AC⊥CD,∴OD⊥CD,
∵点D在⊙O上,
∴CD是⊙O的切线.
(3)如图③,AC⊥BC于点C,BC是⊙O的直径,AB与⊙O相交于点D,EA=EC,求证:ED是⊙O的切线;
证明:连接OD,CD,∵CB是直径,
∴∠CDB=∠ADC=90°,∵EA=EC,
∴ED=EC,∴∠ECD=∠EDC.
∵OD=CO,∴∠OCD=∠CDO,∵AC⊥BC,
∴∠EDO=∠ACB=90°,即ED⊥DO,∵点D在⊙O上,∴ED是⊙O的切线.
【方法归纳】
当切点确定时,常连接圆心与切点,证所连半径与直线垂直
1.当图中有90°角时:①利用等角代换证得垂直;②利用平行线证得垂直; ③利用三角形全等证得垂直.
2.当图中没有90°角时,需要构造:①若图中有已知直径,则利用直径所对的圆周角是90°,构造直角;②若图中有等腰三角形,则利用等腰三角形“三线合一”的性质构造直角.
考向2:切点不确定,作垂直,证半径
如图,在Rt△ABC中,∠ACB=90°,O为AC上一点,以点O为圆心,OC长为半径作圆,过点A作AD⊥BO交BO的延长线于点D,若∠ABD=∠OAD.求证: AB为⊙O的切线.
证明:过点O作OE⊥AB于点E,
∵∠ACB=90°,AD⊥BD,∠AOD=∠BOC,
∴∠OAD=∠OBC,
∵∠ABD=∠OAD,
∴∠ABD=∠OBC,即BD平分∠ABC,
∵OE⊥AB,∴EO=CO.∵CO是⊙O的半径,
∴EO是⊙O的半径,∴AB为⊙O的切线.
【方法归纳】
当切点不确定,证切线时,涉及“垂直+角平分线”的情况下,过圆心作待证切线的垂线,利用角平分线的性质定理证明即可.
突破设问二 切线的性质
考向3:证明线段数量关系
如图,AB是⊙O的直径,BC为⊙O的切线,连接OC与⊙O交于点D,连接AD,若D为OC的中点,求证:BC=AD.
证明:连接BD,
∵BC为⊙O的切线,∴OB⊥BC,∠CBO=90°,
∵AB是⊙O的直径,∴∠ADB=90°,
∵D为OC的中点,∴CD=OD=BD,
∵OB=OD,∴OB=BD,CO=2OB,∴AB=CO,
∴Rt△COB≌Rt△ABD(HL),∴BC=AD.
【方法归纳】
证明线段相等的方法
1.若两条线段共线,则考虑用等腰三角形三线合一的性质或直角三角形斜边中线的性质解决.
2.若两条线段不共线,考虑将这两条线段转化到同一个三角形中,利用等腰三角形或等边三角形的性质求证.
3.若两条线段分别在两个三角形中,可考虑证明三角形全等解决.
4.若所证两条线段平行,可考虑利用特殊四边形对边相等的性质求证.
考向4:证明线段位置关系
如图,AB是⊙O的直径,AD,BC是⊙O的两条弦,∠ABC=2∠A,过点D作⊙O的切线交CB的延长线于点E.求证:CE⊥DE.
证明:连接OD,∵AO=DO,∴∠A=∠ADO,
∴∠BOD=∠A+∠ADO=2∠A,
又∵∠ABC=2∠A,
∴∠ABC=∠DOB,∴OD∥CE,
∵DE是⊙O的切线,
∴OD⊥DE,∴CE⊥DE.
证明两条线段平行的方法
通过等角(同角)的余角(补角)相等及等边对等角等其他角度间的等量代换,得到同位角相等、内错角相等或同旁内角互补,从而证明两线段平行.
证明两条线段垂直的方法
要证两条线段垂直,即要证两条线段所夹的角为90°.常见的方法有两种:
1.当两条线段中的一条与第三条线段垂直时,只需证明另一条线段与第三条线段平行.
2.设法将两条线段构成的夹角放在一个三角形中,通过角度间的等量代换,证得其余两角之和为90°.
考向5:证明角度数量关系
如图,在Rt△ABC中,∠ACB=90°,E是AC上一点,以CE为直径作⊙O,⊙O恰好与AB相切于点D,连接CD.求证:∠B=2∠ACD.
证明:连接OD,
∵AB为⊙O的切线,
∴OD⊥AB,即∠ODA=90°,
∴∠A+∠AOD=90°,
∵∠ACB=90°,
∴∠B+∠A=90°,∴∠AOD=∠B,
∵OD=OC,∴∠ODC=∠OCD,
∴∠AOD=∠ODC+∠OCD=2∠ACD,
∴∠B=2∠ACD.
圆中求角度或证明角度数量关系的方法
1.利用“圆周角定理”“弦、弧、圆心角”关系进行角度转化.
2.根据切线性质构造直角三角形,由两锐角之和等于90°进行角度转化求解.
3.根据两条半径构成的三角形为等腰三角形进行角度转化.
突破设问三 求线段长
方法一:利用勾股定理
如图,CD是⊙O的切线,点C在直径AB的延长线上,若BC=2,CD=3,求⊙O的半径.
【方法归纳】
在圆中求线段长的方法
1.若题干中作辅助线后有直角三角形存在,常运用勾股定理.
2.若题干中含有特殊角(如30°,45°,60°等角度)或出现三角函数sin,cos,tan等时,一般考虑用三角函数解题.
3.题目中无直角三角形时,一般考虑利用三角形相似计算线段长度.
4.运用等面积公式法也可求点到直线的距离.
命题点:切线的有关计算和证明(近5年考查5次)
1.(2022·宁夏第23题8分)如图,以线段AB为直径作⊙O,交射线AC于点C,AD平分∠CAB交⊙O于点D,过点D作直线DE⊥AC于点E,交AB的延长线于点F.连接BD并延长交AC于点M.
(1)求证:直线DE是⊙O的切线;
(2)求证:AB=AM;
(3)若ME=1,∠F=30°,求BF的长.
(1)证明:连接OD,则OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴OD∥AC,
∵DE⊥AC,∴∠ODF=∠AED=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴直线DE是⊙O的切线.
(2)证明:∵OD∥AC,∴∠ODB=∠M,
又∵OD=OB,∴∠ODB=∠ABM,
∴∠M=∠ABM,
∴AB=AM.
(3)解:∵∠AEF=90°,∠F=30°,
∴∠BAM=60°,
∴△ABM是等边三角形,∴∠M=60°,
∵∠DEM=90°,ME=1,∴∠EDM=30°,
∴MD=2ME=2,∴BD=MD=2,
∵∠BDF=∠EDM=30°,∴∠BDF=∠F,
∴BF=BD=2.
(1)证明:连接OC,∵直线DC是⊙O的切线,切点为C,
∴OC⊥DC,
又∵AE⊥DC,垂足为E,
∴OC∥AE,∴∠EAC=∠ACO,
∵OC=OA,∴∠ACO=∠OAC,
∴∠EAC=∠OAC,∴AC平分∠BAE.
3.(2024·福建)如图,已知点A,B在⊙O上,∠AOB=72°,直线MN与⊙O相切,切点为C,且C为的中点,则∠ACM的度数为 ( )
A.18°
B.30°
C.36°
D.72°
A
与圆有关的位置关系
与圆有关的位置关系
与圆有关的位置关系
与圆有关的位置关系
三角形的外接圆、内切圆
与圆有关的位置关系
三角形的外接圆、内切圆
与圆有关的位置关系
1.如果直径为13 cm的圆与一条直线有两个公共点,则圆心到该直线的距离d满足( )
A.d=13 cm
B.d=6.5 cm
C.0 cm≤d<6.5 cm
D.d>6.5 cm
C
B
3.如图,已知在Rt△ABC中,∠B=90°,AB=6,AC=10,点P是Rt△ABC的内心,点P到边AB的距离为 .
2
4.如图,在平面直角坐标系xOy中,点A(0,3),点B(2,1),点C(2,-3).则经画图操作可知:△ABC的外接圆的圆心坐标是 .
(-2,-1)
5.如图,AD切⊙O于点A,AB是⊙O的直径,BD交⊙O于点C.已知AD=2,AB=4,则弦BC的长为 .
6.如图,PA,PB是⊙O的两条切线,A,B是切点,若∠APB=60°,则∠OPB= .
30°
7.如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D.连接BD,若∠C=50°,则∠DBE= .
65°
重难点:与切线相关的证明与计算
突破设问一 切线的判定
考向1:切点确定,连半径,证垂直
(1)如图①,AB是⊙O的直径,AB=AC,点D在⊙O上,DE⊥AC于点E.求证:DE是⊙O的切线;
证明:连接OD,
∵OB=OD,∴∠B=∠1,
∵AB=AC,∴∠B=∠C,
∴∠1=∠C,∴OD∥AC,
∵DE⊥AC,∴OD⊥DE,
又∵点D在⊙O上,∴DE是⊙O的切线.
(2)如图②,AB是⊙O的直径,AD平分∠CAB,点D在⊙O上,CD⊥AC于点C.求证:CD是⊙O的切线;
证明:连接OD,
∵AD平分∠CAB,
∴∠CAD=∠BAD.
又∵OD=OA,∴∠BAD=∠ADO,
∴∠ADO=∠CAD,∴AC∥OD,
∵AC⊥CD,∴OD⊥CD,
∵点D在⊙O上,
∴CD是⊙O的切线.
(3)如图③,AC⊥BC于点C,BC是⊙O的直径,AB与⊙O相交于点D,EA=EC,求证:ED是⊙O的切线;
证明:连接OD,CD,∵CB是直径,
∴∠CDB=∠ADC=90°,∵EA=EC,
∴ED=EC,∴∠ECD=∠EDC.
∵OD=CO,∴∠OCD=∠CDO,∵AC⊥BC,
∴∠EDO=∠ACB=90°,即ED⊥DO,∵点D在⊙O上,∴ED是⊙O的切线.
【方法归纳】
当切点确定时,常连接圆心与切点,证所连半径与直线垂直
1.当图中有90°角时:①利用等角代换证得垂直;②利用平行线证得垂直; ③利用三角形全等证得垂直.
2.当图中没有90°角时,需要构造:①若图中有已知直径,则利用直径所对的圆周角是90°,构造直角;②若图中有等腰三角形,则利用等腰三角形“三线合一”的性质构造直角.
考向2:切点不确定,作垂直,证半径
如图,在Rt△ABC中,∠ACB=90°,O为AC上一点,以点O为圆心,OC长为半径作圆,过点A作AD⊥BO交BO的延长线于点D,若∠ABD=∠OAD.求证: AB为⊙O的切线.
证明:过点O作OE⊥AB于点E,
∵∠ACB=90°,AD⊥BD,∠AOD=∠BOC,
∴∠OAD=∠OBC,
∵∠ABD=∠OAD,
∴∠ABD=∠OBC,即BD平分∠ABC,
∵OE⊥AB,∴EO=CO.∵CO是⊙O的半径,
∴EO是⊙O的半径,∴AB为⊙O的切线.
【方法归纳】
当切点不确定,证切线时,涉及“垂直+角平分线”的情况下,过圆心作待证切线的垂线,利用角平分线的性质定理证明即可.
突破设问二 切线的性质
考向3:证明线段数量关系
如图,AB是⊙O的直径,BC为⊙O的切线,连接OC与⊙O交于点D,连接AD,若D为OC的中点,求证:BC=AD.
证明:连接BD,
∵BC为⊙O的切线,∴OB⊥BC,∠CBO=90°,
∵AB是⊙O的直径,∴∠ADB=90°,
∵D为OC的中点,∴CD=OD=BD,
∵OB=OD,∴OB=BD,CO=2OB,∴AB=CO,
∴Rt△COB≌Rt△ABD(HL),∴BC=AD.
【方法归纳】
证明线段相等的方法
1.若两条线段共线,则考虑用等腰三角形三线合一的性质或直角三角形斜边中线的性质解决.
2.若两条线段不共线,考虑将这两条线段转化到同一个三角形中,利用等腰三角形或等边三角形的性质求证.
3.若两条线段分别在两个三角形中,可考虑证明三角形全等解决.
4.若所证两条线段平行,可考虑利用特殊四边形对边相等的性质求证.
考向4:证明线段位置关系
如图,AB是⊙O的直径,AD,BC是⊙O的两条弦,∠ABC=2∠A,过点D作⊙O的切线交CB的延长线于点E.求证:CE⊥DE.
证明:连接OD,∵AO=DO,∴∠A=∠ADO,
∴∠BOD=∠A+∠ADO=2∠A,
又∵∠ABC=2∠A,
∴∠ABC=∠DOB,∴OD∥CE,
∵DE是⊙O的切线,
∴OD⊥DE,∴CE⊥DE.
证明两条线段平行的方法
通过等角(同角)的余角(补角)相等及等边对等角等其他角度间的等量代换,得到同位角相等、内错角相等或同旁内角互补,从而证明两线段平行.
证明两条线段垂直的方法
要证两条线段垂直,即要证两条线段所夹的角为90°.常见的方法有两种:
1.当两条线段中的一条与第三条线段垂直时,只需证明另一条线段与第三条线段平行.
2.设法将两条线段构成的夹角放在一个三角形中,通过角度间的等量代换,证得其余两角之和为90°.
考向5:证明角度数量关系
如图,在Rt△ABC中,∠ACB=90°,E是AC上一点,以CE为直径作⊙O,⊙O恰好与AB相切于点D,连接CD.求证:∠B=2∠ACD.
证明:连接OD,
∵AB为⊙O的切线,
∴OD⊥AB,即∠ODA=90°,
∴∠A+∠AOD=90°,
∵∠ACB=90°,
∴∠B+∠A=90°,∴∠AOD=∠B,
∵OD=OC,∴∠ODC=∠OCD,
∴∠AOD=∠ODC+∠OCD=2∠ACD,
∴∠B=2∠ACD.
圆中求角度或证明角度数量关系的方法
1.利用“圆周角定理”“弦、弧、圆心角”关系进行角度转化.
2.根据切线性质构造直角三角形,由两锐角之和等于90°进行角度转化求解.
3.根据两条半径构成的三角形为等腰三角形进行角度转化.
突破设问三 求线段长
方法一:利用勾股定理
如图,CD是⊙O的切线,点C在直径AB的延长线上,若BC=2,CD=3,求⊙O的半径.
【方法归纳】
在圆中求线段长的方法
1.若题干中作辅助线后有直角三角形存在,常运用勾股定理.
2.若题干中含有特殊角(如30°,45°,60°等角度)或出现三角函数sin,cos,tan等时,一般考虑用三角函数解题.
3.题目中无直角三角形时,一般考虑利用三角形相似计算线段长度.
4.运用等面积公式法也可求点到直线的距离.
命题点:切线的有关计算和证明(近5年考查5次)
1.(2022·宁夏第23题8分)如图,以线段AB为直径作⊙O,交射线AC于点C,AD平分∠CAB交⊙O于点D,过点D作直线DE⊥AC于点E,交AB的延长线于点F.连接BD并延长交AC于点M.
(1)求证:直线DE是⊙O的切线;
(2)求证:AB=AM;
(3)若ME=1,∠F=30°,求BF的长.
(1)证明:连接OD,则OD=OA,
∴∠ODA=∠OAD,
∵AD平分∠CAB,
∴∠OAD=∠DAC,
∴∠ODA=∠DAC,
∴OD∥AC,
∵DE⊥AC,∴∠ODF=∠AED=90°,
∵OD是⊙O的半径,且DE⊥OD,
∴直线DE是⊙O的切线.
(2)证明:∵OD∥AC,∴∠ODB=∠M,
又∵OD=OB,∴∠ODB=∠ABM,
∴∠M=∠ABM,
∴AB=AM.
(3)解:∵∠AEF=90°,∠F=30°,
∴∠BAM=60°,
∴△ABM是等边三角形,∴∠M=60°,
∵∠DEM=90°,ME=1,∴∠EDM=30°,
∴MD=2ME=2,∴BD=MD=2,
∵∠BDF=∠EDM=30°,∴∠BDF=∠F,
∴BF=BD=2.
(1)证明:连接OC,∵直线DC是⊙O的切线,切点为C,
∴OC⊥DC,
又∵AE⊥DC,垂足为E,
∴OC∥AE,∴∠EAC=∠ACO,
∵OC=OA,∴∠ACO=∠OAC,
∴∠EAC=∠OAC,∴AC平分∠BAE.
3.(2024·福建)如图,已知点A,B在⊙O上,∠AOB=72°,直线MN与⊙O相切,切点为C,且C为的中点,则∠ACM的度数为 ( )
A.18°
B.30°
C.36°
D.72°
A
同课章节目录
