中考数学复习第七章图形变化微专题(七)几何最值问题第2课时利用两点之间线段最短求最值课件
文档属性
| 名称 | 中考数学复习第七章图形变化微专题(七)几何最值问题第2课时利用两点之间线段最短求最值课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 662.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:16:00 | ||
图片预览






文档简介
(共18张PPT)
类型1:求线段和最小值
如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AB边上一点,且AE=2,则线段EF+CF的最小值为 .
【思路点拨】连接EC交AD于点F′,此时EF′+CF′=CE最小.
【方法归纳】
1.异侧线段和最小值问题
如图,两定点A,B位于直线l异侧,在直线l上找一点P,使PA+PB值最小.
解题思路:根据两点之间线段最短,PA+PB的最小值即为线段AB的长,连接AB交直线l于点P,点P即为所求.
如图,在菱形ABCD中,AB=6,E,F分别是AB,BC的中点,点P在对角线AC上,连接PE,PF,则PE+PF的最小值为 .
【思路点拨】由菱形的对称性得直线AC是菱形的对称轴,取点E 关于AC的对称点E′,连接E′F,交AC于点P′,PE+PF的最小值为E′F的长.
6
2.同侧线段和最小值问题
如图,两定点A,B位于直线l同侧,在直线l上找一点P,使得PA+PB值最小.
解题思路:将两定点同侧转化为异侧问题,即可解决.作点B关于直线l的对称点B′,连接AB′,与直线l交于点P,点P即为所求.
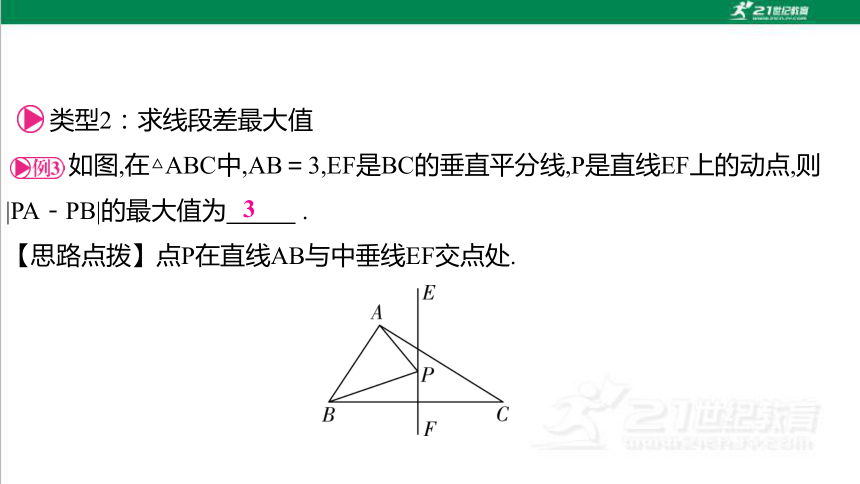
类型2:求线段差最大值
如图,在△ABC中,AB=3,EF是BC的垂直平分线,P是直线EF上的动点,则 |PA-PB|的最大值为 .
【思路点拨】点P在直线AB与中垂线EF交点处.
3
3.同侧线段差最大值问题
如图,两定点A,B位于直线l同侧,在直线l上找一点P,使|PA-PB|值最大.
解题思路:根据两边之差小于第三边,|PA-PB|的最大值即为AB的长,连接AB并延长,与直线l交于点P,点P即为所求.
如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=4,E为射线AD上一点,∠BAD=15°,连接BE,CE,则CE-BE的最大值为 .
【思路点拨】作点B关于AD的对称点B′,连接CB′并延长,交AD于E′.△AB′C为等腰直角三角形.当点E,B′,C三点共线时,即点E位于点E′处时,CE-BE的值最大,即CB′的长.
4.异侧线段差最大值问题
问题:两定点A,B位于直线l异侧,在直线l上找一点P,使得|PA-PB|值最大.
解题思路:将两定点异侧转化为同侧问题,即可解决.作点B关于直线l的对称点B′, 连接AB′并延长,与直线l交于点P,点P即为所求.
如图,在△ABC中,∠ABC=45°,P为AC上一定点,BP=6,D,E分别是AB,BC上的动点,连接DP,EP,DE,则△DEP周长的最小值为 .
【思路点拨】分别作点P关于AB,BC的对称点P′,P″,并连接P′P″,交AB,BC于点D′,E′,此时△DEP的周长最小.
【方法归纳】如图,P是∠AOB内部的一定点,在OA上找一点M,在OB上找一点N,使得△PMN周长最小.
解题思路:要使△PMN周长最小,即PM+MN+PN值最小,根据两点之间线段最短,将三条线段转化到同一直线上.分别作点P关于OA,OB的对称点P′,P″,连接P′P″,交OA,OB于点M,N,点M,N即为所求.
类型3:两定两动(两点两线)
如图,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,G,H分别是边BC,CD上的动点,则四边形EFGH周长的最小值为 .
【思路点拨】作点E关于CD的对称点E′,作点F关于BC的对称点F′,连接E′F′,分别交CD于点H′,交BC于点G′,即可求出四边形EFGH周长的最小值.
【方法归纳】如图,P,Q是∠AOB内部的两定点,在OA上找一点M,在OB上找一点N,使得四边形PQNM周长最小.
解题思路:要使四边形PQNM周长最小,PQ为定值,即求得PM+MN+NQ的最小值即可,需将三条线段转化到同一直线上,分别作点P,Q关于OA,OB的对称点P′,Q′,连接P′Q′,交OA,OB于点M,N,点M,N即为所求.
1.如图,在矩形ABCD中,M是AB边上一点,且BM=5,P是直线BC上一动点,若CD=2BC=8,则|PD-PM|的最大值为 .
5
3.如图,已知正方形ABCD的边长为3,E是AB边上的一动点,连接ED,将ED绕点E顺时针旋转90°到EF,连接DF,CF,则DF+CF的最小值是 .
【解析】作FG⊥AB延长线于点G,证△AED≌△GFE(AAS),得AE=BG=FG,确定F在射线BF上运动,作点C关于BF的对称点C′,由∠FBG=45°确定C′在AB延长线上,当D,F,C′三点共线时,DF+CF=DC′最小.
4.如图,在边长为4的正方形ABCD中,E为AB上一点,且AE=1,F为CD的中点,P为AD边上的一个动点,连接PE,PF,则PE+PF的最小值为 .
5
简写过程:
作点F关于AD的对称点M,连接PM,EM,
则PE+PF=PE+PM≥EM,
∴当E,P,M三点共线时,PE+PF的值最小,
最小值为EM的长,过点E作EH⊥CD于点H,
则EH=BC=4,DH=AE=1,根据对称性可知DM=DF=2,即解.
类型1:求线段和最小值
如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是线段AD上的动点,E是AB边上一点,且AE=2,则线段EF+CF的最小值为 .
【思路点拨】连接EC交AD于点F′,此时EF′+CF′=CE最小.
【方法归纳】
1.异侧线段和最小值问题
如图,两定点A,B位于直线l异侧,在直线l上找一点P,使PA+PB值最小.
解题思路:根据两点之间线段最短,PA+PB的最小值即为线段AB的长,连接AB交直线l于点P,点P即为所求.
如图,在菱形ABCD中,AB=6,E,F分别是AB,BC的中点,点P在对角线AC上,连接PE,PF,则PE+PF的最小值为 .
【思路点拨】由菱形的对称性得直线AC是菱形的对称轴,取点E 关于AC的对称点E′,连接E′F,交AC于点P′,PE+PF的最小值为E′F的长.
6
2.同侧线段和最小值问题
如图,两定点A,B位于直线l同侧,在直线l上找一点P,使得PA+PB值最小.
解题思路:将两定点同侧转化为异侧问题,即可解决.作点B关于直线l的对称点B′,连接AB′,与直线l交于点P,点P即为所求.
类型2:求线段差最大值
如图,在△ABC中,AB=3,EF是BC的垂直平分线,P是直线EF上的动点,则 |PA-PB|的最大值为 .
【思路点拨】点P在直线AB与中垂线EF交点处.
3
3.同侧线段差最大值问题
如图,两定点A,B位于直线l同侧,在直线l上找一点P,使|PA-PB|值最大.
解题思路:根据两边之差小于第三边,|PA-PB|的最大值即为AB的长,连接AB并延长,与直线l交于点P,点P即为所求.
如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=4,E为射线AD上一点,∠BAD=15°,连接BE,CE,则CE-BE的最大值为 .
【思路点拨】作点B关于AD的对称点B′,连接CB′并延长,交AD于E′.△AB′C为等腰直角三角形.当点E,B′,C三点共线时,即点E位于点E′处时,CE-BE的值最大,即CB′的长.
4.异侧线段差最大值问题
问题:两定点A,B位于直线l异侧,在直线l上找一点P,使得|PA-PB|值最大.
解题思路:将两定点异侧转化为同侧问题,即可解决.作点B关于直线l的对称点B′, 连接AB′并延长,与直线l交于点P,点P即为所求.
如图,在△ABC中,∠ABC=45°,P为AC上一定点,BP=6,D,E分别是AB,BC上的动点,连接DP,EP,DE,则△DEP周长的最小值为 .
【思路点拨】分别作点P关于AB,BC的对称点P′,P″,并连接P′P″,交AB,BC于点D′,E′,此时△DEP的周长最小.
【方法归纳】如图,P是∠AOB内部的一定点,在OA上找一点M,在OB上找一点N,使得△PMN周长最小.
解题思路:要使△PMN周长最小,即PM+MN+PN值最小,根据两点之间线段最短,将三条线段转化到同一直线上.分别作点P关于OA,OB的对称点P′,P″,连接P′P″,交OA,OB于点M,N,点M,N即为所求.
类型3:两定两动(两点两线)
如图,在矩形ABCD中,AB=4,AD=6,AE=4,AF=2,G,H分别是边BC,CD上的动点,则四边形EFGH周长的最小值为 .
【思路点拨】作点E关于CD的对称点E′,作点F关于BC的对称点F′,连接E′F′,分别交CD于点H′,交BC于点G′,即可求出四边形EFGH周长的最小值.
【方法归纳】如图,P,Q是∠AOB内部的两定点,在OA上找一点M,在OB上找一点N,使得四边形PQNM周长最小.
解题思路:要使四边形PQNM周长最小,PQ为定值,即求得PM+MN+NQ的最小值即可,需将三条线段转化到同一直线上,分别作点P,Q关于OA,OB的对称点P′,Q′,连接P′Q′,交OA,OB于点M,N,点M,N即为所求.
1.如图,在矩形ABCD中,M是AB边上一点,且BM=5,P是直线BC上一动点,若CD=2BC=8,则|PD-PM|的最大值为 .
5
3.如图,已知正方形ABCD的边长为3,E是AB边上的一动点,连接ED,将ED绕点E顺时针旋转90°到EF,连接DF,CF,则DF+CF的最小值是 .
【解析】作FG⊥AB延长线于点G,证△AED≌△GFE(AAS),得AE=BG=FG,确定F在射线BF上运动,作点C关于BF的对称点C′,由∠FBG=45°确定C′在AB延长线上,当D,F,C′三点共线时,DF+CF=DC′最小.
4.如图,在边长为4的正方形ABCD中,E为AB上一点,且AE=1,F为CD的中点,P为AD边上的一个动点,连接PE,PF,则PE+PF的最小值为 .
5
简写过程:
作点F关于AD的对称点M,连接PM,EM,
则PE+PF=PE+PM≥EM,
∴当E,P,M三点共线时,PE+PF的值最小,
最小值为EM的长,过点E作EH⊥CD于点H,
则EH=BC=4,DH=AE=1,根据对称性可知DM=DF=2,即解.
同课章节目录
