中考数学复习第七章图形变化第三节图形的平移、对称与旋转课件
文档属性
| 名称 | 中考数学复习第七章图形变化第三节图形的平移、对称与旋转课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:16:00 | ||
图片预览









文档简介
(共34张PPT)
图形的平移、 对称与旋转
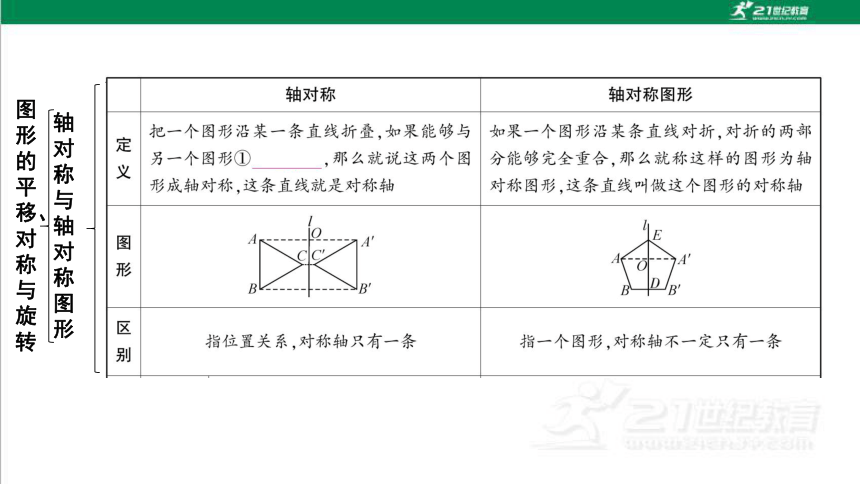
轴对称与轴对称图形
图形的平移、 对称与旋转
轴对称与轴对称图形
图形的平移、 对称与旋转
图形的平移、 对称与旋转
图形的平移、 对称与旋转
图形的平移、 对称与旋转
图形的平移、 对称与旋转
图形的平移、 对称与旋转
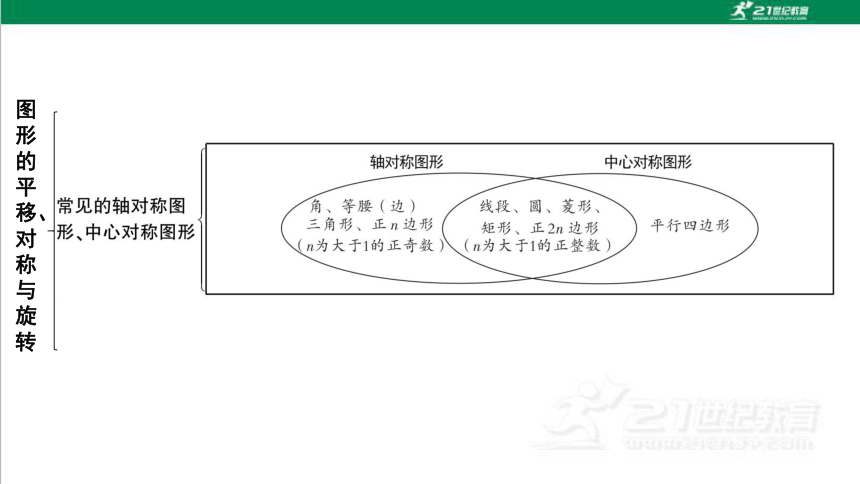
1.正方形、平行四边形、三角形、圆中,其中轴对称图形有 个,中心对称图形有 个.
2
3
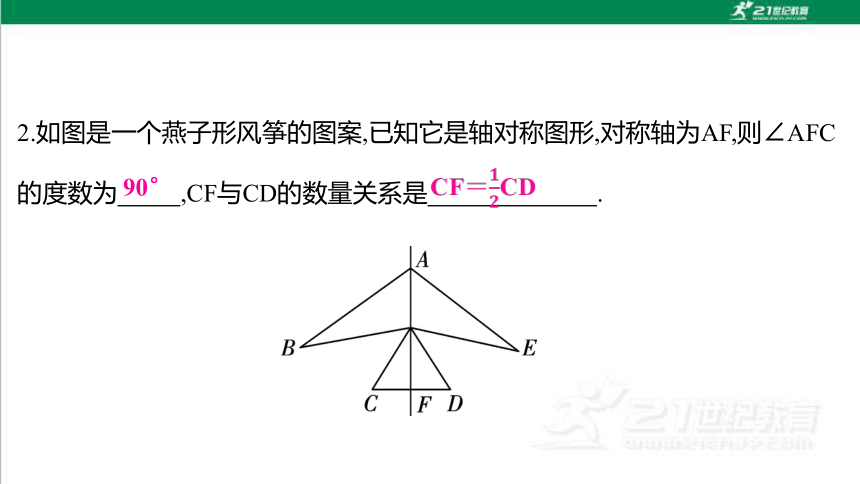
2.如图是一个燕子形风筝的图案,已知它是轴对称图形,对称轴为AF,则∠AFC的度数为 ,CF与CD的数量关系是 .
90°
3.如图,将△ABC绕着点A逆时针旋转得到△ADE,使得点B的对应点D落在边AC的延长线上,若AB=15,AE=10,则线段CD的长为 ;若∠BAC=20°,则旋转角为 ,∠BAE= .
5
20°
40°
4.如图,在△ABC中,将△ABC沿BC方向平移,得到△DEF,DE交AC于点G,连接AD.
(1)△ABC △DEF,AD与CF的数量关系为 ,位置关系为 ;
(2)AD,BC,BF之间的数量关系为 ;
(3)四边形ABED的形状为 ;
(4)若∠BAC=105°,则∠DGC= ;
(5)若△ABC的周长为8,平移距离为2,则四边形ABFD的周长为 ;
(6)若S△ABC=6,E为BC的中点,则S四边形GCFD= .
AD=CF
AD∥CF
BF=AD+BC
平行四边形
75°
12
≌
5.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,将△ABC绕点C按顺时针方向旋转,得到△EDC,点D落在AB边上,DE交AC于点F.
(1)DE的长为 ,∠CDE= ;
(2)∠CFE= ,AD的长为 ;
(3)请写出图中的全等三角形和相似三角形:
.
4
60°
90°
2
△ABC≌△EDC,△ADF≌△CDF,△ADF∽△ABC∽△EDC∽△ECF∽△CDF
6.若将点M(a,b)向上平移2个单位长度得到点B,点B关于x轴的对称点坐标仍是M(a,b),则b= .
7.平面直角坐标系中有点P,Q(2,-3),M(-1,2).如果PQ∥x轴,PM∥y轴,那么点P关于原点O对称的点的坐标是 .
-1
(1,3)
如图①,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.
(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上.
Ⅰ)求∠ADB的度数;
Ⅱ)将射线AD顺时针旋转90°交直线l于点E,
写出线段AD,BD,CD的数量关系;
解:Ⅰ)∵∠BAC=90°,且AB=AC,∴∠ACB=∠ABC=45°,
∵∠BAC=∠BDC=90°,∴A,B,C,D四点共圆,∴∠ADB=∠ACB=45°.
(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图②位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;
重难点2:折叠性质的相关证明与计算
如图,在矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,BE与CD相交于点G,PE与CD相交于点O,且OE=OD.
(1)求证:DP=EG;
(2)求AP的长.
(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=90°,
AB=CD=4,AD=BC=3,
∵将△ABP沿BP翻折至△EBP,BE与CD相交于点G,PE与CD相交于点O,
∴∠A=∠E=∠D=90°,
∴△PDO≌△GEO(ASA),∴OG=OP,DP=EG.
(2)解:易得DG=PE=PA,设AP=x,则
PD=EG=3-x,DG=AP=x,
∴BG=BE-EG=1+x,CG=DC-DG=4-x,
在Rt△BCG中,BC2+CG2=BG2,即
32+(4-x)2=(1+x)2,解得x=2.4,∴AP=2.4.
命题点1:图形的对称(近5年考查2次)
1.(2023·宁夏第2题3分)下面是由七巧板拼成的图形(只考虑外形,忽略内部轮廓),其中是轴对称图形的是 ( )
C
2.(2023·宁夏第16题3分)如图是由边长为1的小正方形组成的9×6网格,点A,B,C,D,E,F,G均在格点上.下列结论:
①点D与点F关于点E中心对称;
②连接FB,FC,FE,则FC平分∠BFE;
③连接AG,则点B,F到线段AG的距离相等.
其中正确结论的序号是 (选填序号).
①②③
命题点2:图形的平移(近5年考查2次)
3.(2022·宁夏第13题3分)如图,点B的坐标是(0,3),将△OAB沿x轴向右平移至△CDE,点B的对应点E恰好落在直线y=2x-3上,则点A移动的距离是 .
3
【解析】令y=2x-3=3,∴x=3,∴点E的坐标为(3,3),∴△OAB沿x轴向右平移3个单位长度得到△CDE,∴点A移动的距离为3.
命题点3:图形的旋转(近5年考查4次)
4.(2022·宁夏第15题3分)如图,直线a∥b,△AOB的边OB在直线b上,
∠AOB=55°,将△AOB绕点O顺时针旋转75°至△A1OB1,边A1O交直线a于点C,则∠1= .
50°
命题点4:网格作图题(近5年考查6次)
5.(2022·宁夏第17题6分)如图,是边长为1的小正方形组成的8×8方格,线段AB的端点在格点上.建立平面直角坐标系,使点A,B的坐标分别为(2,1)和(-1,3).
(1)画出该平面直角坐标系xOy;
(2)画出线段AB关于原点O成中心对称
的线段A1B1;
(3)画出以点A,B,O为其中三个顶点
的平行四边形. (画出一个即可)
解:(1)如图,平面直角坐标系xOy即为所求.
(2)如图,线段A1B1即为所求.
(3)如图, AOBD即为所求(答案不唯一).
6.(2021·宁夏第17题6分)如图,在平面直角坐标系中,已知线段A1B1与线段AB关于y轴对称,点A1(-2,1)是点A的对应点,点B1是点B(4,2)的对应点.
(1)画出线段AB和A1B1;
(2)画出将线段A1B1绕点A1
逆时针旋转90°所得的线段A1B2,
并求出点B1旋转到点B2所经过的路径长.
7.(2024·自贡)我国汉代数学家赵爽在他所著《勾股圆方图注》中,运用弦图(如图所示)巧妙地证明了勾股定理.“赵爽弦图”曾作为国际数学家大会的会徽图案.下列关于“赵爽弦图”说法正确的是 ( )
A.是轴对称图形
B.是中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形也不是中心对称图形
B
8.(2024·连云港)如图,正方形中有一个由若干个长方形组成的对称图案,其中正方形边长是80 cm,则图中阴影图形的周长是 ( )
A.440 cm
B.320 cm
C.280 cm
D.160 cm
A
图形的平移、 对称与旋转
轴对称与轴对称图形
图形的平移、 对称与旋转
轴对称与轴对称图形
图形的平移、 对称与旋转
图形的平移、 对称与旋转
图形的平移、 对称与旋转
图形的平移、 对称与旋转
图形的平移、 对称与旋转
图形的平移、 对称与旋转
1.正方形、平行四边形、三角形、圆中,其中轴对称图形有 个,中心对称图形有 个.
2
3
2.如图是一个燕子形风筝的图案,已知它是轴对称图形,对称轴为AF,则∠AFC的度数为 ,CF与CD的数量关系是 .
90°
3.如图,将△ABC绕着点A逆时针旋转得到△ADE,使得点B的对应点D落在边AC的延长线上,若AB=15,AE=10,则线段CD的长为 ;若∠BAC=20°,则旋转角为 ,∠BAE= .
5
20°
40°
4.如图,在△ABC中,将△ABC沿BC方向平移,得到△DEF,DE交AC于点G,连接AD.
(1)△ABC △DEF,AD与CF的数量关系为 ,位置关系为 ;
(2)AD,BC,BF之间的数量关系为 ;
(3)四边形ABED的形状为 ;
(4)若∠BAC=105°,则∠DGC= ;
(5)若△ABC的周长为8,平移距离为2,则四边形ABFD的周长为 ;
(6)若S△ABC=6,E为BC的中点,则S四边形GCFD= .
AD=CF
AD∥CF
BF=AD+BC
平行四边形
75°
12
≌
5.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AB=4,将△ABC绕点C按顺时针方向旋转,得到△EDC,点D落在AB边上,DE交AC于点F.
(1)DE的长为 ,∠CDE= ;
(2)∠CFE= ,AD的长为 ;
(3)请写出图中的全等三角形和相似三角形:
.
4
60°
90°
2
△ABC≌△EDC,△ADF≌△CDF,△ADF∽△ABC∽△EDC∽△ECF∽△CDF
6.若将点M(a,b)向上平移2个单位长度得到点B,点B关于x轴的对称点坐标仍是M(a,b),则b= .
7.平面直角坐标系中有点P,Q(2,-3),M(-1,2).如果PQ∥x轴,PM∥y轴,那么点P关于原点O对称的点的坐标是 .
-1
(1,3)
如图①,点B在直线l上,过点B构建等腰直角三角形ABC,使∠BAC=90°,且AB=AC,过点C作CD⊥直线l于点D,连接AD.
(1)小亮在研究这个图形时发现,∠BAC=∠BDC=90°,点A,D应该在以BC为直径的圆上.
Ⅰ)求∠ADB的度数;
Ⅱ)将射线AD顺时针旋转90°交直线l于点E,
写出线段AD,BD,CD的数量关系;
解:Ⅰ)∵∠BAC=90°,且AB=AC,∴∠ACB=∠ABC=45°,
∵∠BAC=∠BDC=90°,∴A,B,C,D四点共圆,∴∠ADB=∠ACB=45°.
(2)小亮将等腰直角三角形ABC绕点B在平面内旋转,当旋转到图②位置时,线段AD,BD,CD的数量关系是否变化,请说明理由;
重难点2:折叠性质的相关证明与计算
如图,在矩形ABCD中,AB=4,BC=3,P为AD上一点,将△ABP沿BP翻折至△EBP,BE与CD相交于点G,PE与CD相交于点O,且OE=OD.
(1)求证:DP=EG;
(2)求AP的长.
(1)证明:∵四边形ABCD是矩形,∴∠A=∠D=90°,
AB=CD=4,AD=BC=3,
∵将△ABP沿BP翻折至△EBP,BE与CD相交于点G,PE与CD相交于点O,
∴∠A=∠E=∠D=90°,
∴△PDO≌△GEO(ASA),∴OG=OP,DP=EG.
(2)解:易得DG=PE=PA,设AP=x,则
PD=EG=3-x,DG=AP=x,
∴BG=BE-EG=1+x,CG=DC-DG=4-x,
在Rt△BCG中,BC2+CG2=BG2,即
32+(4-x)2=(1+x)2,解得x=2.4,∴AP=2.4.
命题点1:图形的对称(近5年考查2次)
1.(2023·宁夏第2题3分)下面是由七巧板拼成的图形(只考虑外形,忽略内部轮廓),其中是轴对称图形的是 ( )
C
2.(2023·宁夏第16题3分)如图是由边长为1的小正方形组成的9×6网格,点A,B,C,D,E,F,G均在格点上.下列结论:
①点D与点F关于点E中心对称;
②连接FB,FC,FE,则FC平分∠BFE;
③连接AG,则点B,F到线段AG的距离相等.
其中正确结论的序号是 (选填序号).
①②③
命题点2:图形的平移(近5年考查2次)
3.(2022·宁夏第13题3分)如图,点B的坐标是(0,3),将△OAB沿x轴向右平移至△CDE,点B的对应点E恰好落在直线y=2x-3上,则点A移动的距离是 .
3
【解析】令y=2x-3=3,∴x=3,∴点E的坐标为(3,3),∴△OAB沿x轴向右平移3个单位长度得到△CDE,∴点A移动的距离为3.
命题点3:图形的旋转(近5年考查4次)
4.(2022·宁夏第15题3分)如图,直线a∥b,△AOB的边OB在直线b上,
∠AOB=55°,将△AOB绕点O顺时针旋转75°至△A1OB1,边A1O交直线a于点C,则∠1= .
50°
命题点4:网格作图题(近5年考查6次)
5.(2022·宁夏第17题6分)如图,是边长为1的小正方形组成的8×8方格,线段AB的端点在格点上.建立平面直角坐标系,使点A,B的坐标分别为(2,1)和(-1,3).
(1)画出该平面直角坐标系xOy;
(2)画出线段AB关于原点O成中心对称
的线段A1B1;
(3)画出以点A,B,O为其中三个顶点
的平行四边形. (画出一个即可)
解:(1)如图,平面直角坐标系xOy即为所求.
(2)如图,线段A1B1即为所求.
(3)如图, AOBD即为所求(答案不唯一).
6.(2021·宁夏第17题6分)如图,在平面直角坐标系中,已知线段A1B1与线段AB关于y轴对称,点A1(-2,1)是点A的对应点,点B1是点B(4,2)的对应点.
(1)画出线段AB和A1B1;
(2)画出将线段A1B1绕点A1
逆时针旋转90°所得的线段A1B2,
并求出点B1旋转到点B2所经过的路径长.
7.(2024·自贡)我国汉代数学家赵爽在他所著《勾股圆方图注》中,运用弦图(如图所示)巧妙地证明了勾股定理.“赵爽弦图”曾作为国际数学家大会的会徽图案.下列关于“赵爽弦图”说法正确的是 ( )
A.是轴对称图形
B.是中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形也不是中心对称图形
B
8.(2024·连云港)如图,正方形中有一个由若干个长方形组成的对称图案,其中正方形边长是80 cm,则图中阴影图形的周长是 ( )
A.440 cm
B.320 cm
C.280 cm
D.160 cm
A
同课章节目录
