中考数学复习第七章图形变化微专题(六)无刻度直尺作图课件
文档属性
| 名称 | 中考数学复习第七章图形变化微专题(六)无刻度直尺作图课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 874.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:16:00 | ||
图片预览



文档简介
(共18张PPT)
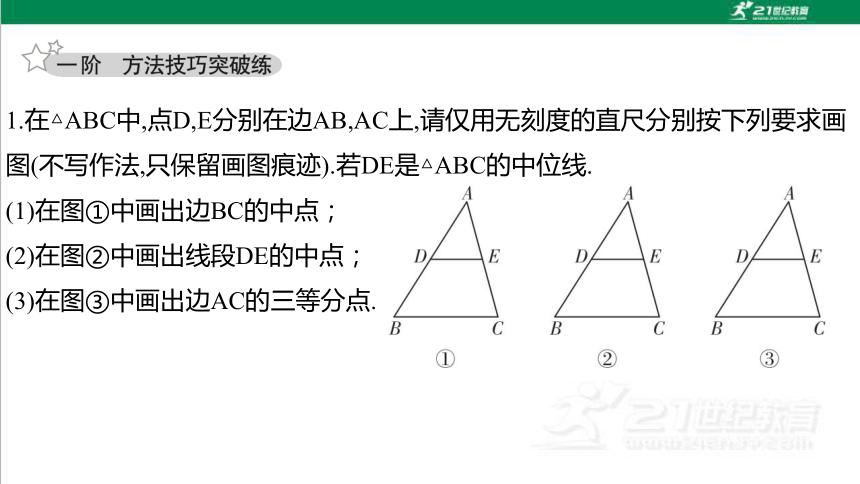
1.在△ABC中,点D,E分别在边AB,AC上,请仅用无刻度的直尺分别按下列要求画图(不写作法,只保留画图痕迹).若DE是△ABC的中位线.
(1)在图①中画出边BC的中点;
(2)在图②中画出线段DE的中点;
(3)在图③中画出边AC的三等分点.
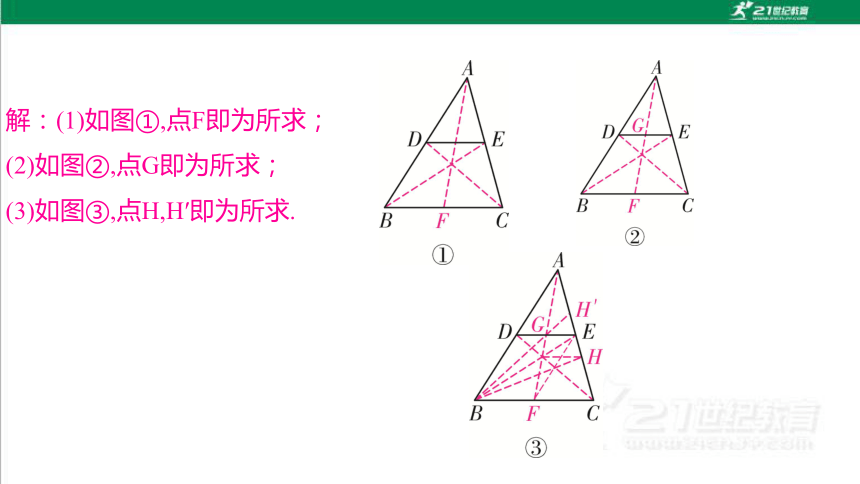
解:(1)如图①,点F即为所求;
(2)如图②,点G即为所求;
(3)如图③,点H,H′即为所求.
【方法归纳】三角形中,已知两边中点:
(1)画第三边中点时,一般运用“三角形三条中线交于一点”;
(2)画某条中位线的中点时,先确定该中位线对应的底边中线,根据相似三角形的性质,由底边中线与中位线的交点确定中点;
(3)一般地,已知中位线,可由中位线直接得到比例为1∶2的线段,由中位线的性质可构造全等三角形,得到相等线段,也可由相似三角形的性质得到1∶3,1∶4的线段.
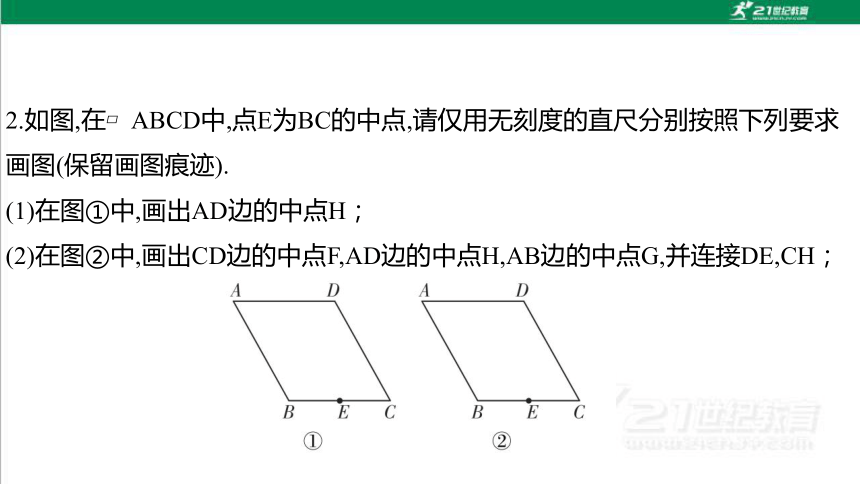
2.如图,在 ABCD中,点E为BC的中点,请仅用无刻度的直尺分别按照下列要求画图(保留画图痕迹).
(1)在图①中,画出AD边的中点H;
(2)在图②中,画出CD边的中点F,AD边的中点H,AB边的中点G,并连接DE,CH;
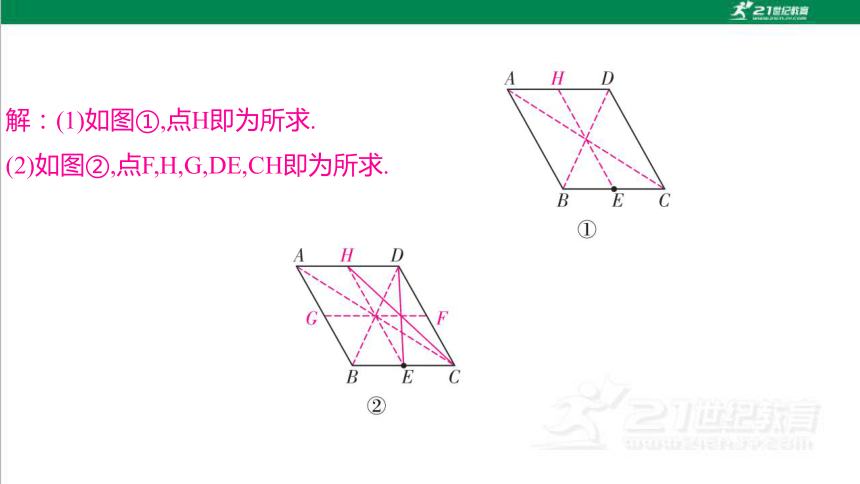
解:(1)如图①,点H即为所求.
(2)如图②,点F,H,G,DE,CH即为所求.
【方法归纳】
特殊四边形中,已知一边中点,由对称性画出其他三边的中点;将特殊四边形的四个中点呈“十字相连”,得到四个与原四边形相似的小的四边形,继续作这些小四边形的中点并呈“十字相连”,得到一个网格,每一个中点均是网格的格点,且该网格具有该特殊四边形的一切性质.
3.如图,△ABC的三个顶点分别在正方形网格的格点上,请按要求完成下列各题:
(1)在图①中找一格点D,连接BD,使∠ABD与∠BAC互补;
(2)在图②中找一格点E,连接BE,使∠ABE与∠BAC互余;
(3)在图③中找一格点F,连接BF,使∠ABF=45°.
【思路点拨】(1)作BD∥AC;(2)将(1)中BD旋转90°,或作BE⊥AC;(3)作等腰直角三角形ABF.
解:(1)如图①,点D即为所求.(2)如图②,点E 即为所求.(答案不唯一)(3)如图③,点F即为所求.
【方法归纳】无刻度直尺作图常考模型
模型一 特殊角问题
举例:在图①中,找一格点C,使∠BAC=45°(画出一种即可).
原理:由∠BAC=45°,可得以点B或点C为直角顶点的等腰三角形ABC,再结合点C为格点,即可画出符合要求的图形.
作答:∠BAC如图②所示.(答案不唯一,作出其中一种即可).
模型二 找中点或n等分点问题
举例:在图③中找出线段AB的中点P以及线段AB的一个离点B最近的四等分点Q.
原理:全等三角形对应边相等;相似三角形对应边成比例.
作答:点P如图④所示;点Q如图⑤所示.
模型三 面积相等问题
举例:在图⑥中找一格点E,使S△ABE=S△ABC.
原理:平行线间的距离相等.将固定的一边AB在网格中进行平移,直至经过点C,即可作出符合要求的格点图形.
作答:点E如图⑦所示.
4.在△ABC中,AB=AC,请仅用无刻度的直尺分别按下列要求画图(不写作法,只保留作图痕迹)
(1)点D,E分别是AB,AC的中点,在图①中画出BC边上的高线;
(2)BE⊥AC,CD⊥AB,在图②中画出∠BAC的平分线.
解:(1)如图①,AP即为所求.
(2)如图②,AG即为所求.
5.(2022·武汉)如图是由小正方形组成的9×6网格,每个小正方形的顶点叫做格点.△ABC的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图①中,D,E分别是边AB,
AC与网格线的交点.先将点B绕
点E旋转180°得到点F,画出点F,
再在AC上画点G,使DG∥BC;
(2)在图②中,P是边AB上一点,∠BAC=α.先将AB绕点A逆时针旋转2α,得到线段AH,画出线段AH,再画点Q,使P,Q两点关于直线AC对称.
解:(1)作图如图①所示.
(2)作图如图②所示.
6.(2024·江西)如图,AC为菱形ABCD的对角线,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹)
(1)如图①,过点B作AC的垂线;
(2)如图②,点E为线段AB的中点,过点B作AC的平行线.
解:(1)如图所示,BD即为所求.
(2)如图所示,BM即为所求.
1.在△ABC中,点D,E分别在边AB,AC上,请仅用无刻度的直尺分别按下列要求画图(不写作法,只保留画图痕迹).若DE是△ABC的中位线.
(1)在图①中画出边BC的中点;
(2)在图②中画出线段DE的中点;
(3)在图③中画出边AC的三等分点.
解:(1)如图①,点F即为所求;
(2)如图②,点G即为所求;
(3)如图③,点H,H′即为所求.
【方法归纳】三角形中,已知两边中点:
(1)画第三边中点时,一般运用“三角形三条中线交于一点”;
(2)画某条中位线的中点时,先确定该中位线对应的底边中线,根据相似三角形的性质,由底边中线与中位线的交点确定中点;
(3)一般地,已知中位线,可由中位线直接得到比例为1∶2的线段,由中位线的性质可构造全等三角形,得到相等线段,也可由相似三角形的性质得到1∶3,1∶4的线段.
2.如图,在 ABCD中,点E为BC的中点,请仅用无刻度的直尺分别按照下列要求画图(保留画图痕迹).
(1)在图①中,画出AD边的中点H;
(2)在图②中,画出CD边的中点F,AD边的中点H,AB边的中点G,并连接DE,CH;
解:(1)如图①,点H即为所求.
(2)如图②,点F,H,G,DE,CH即为所求.
【方法归纳】
特殊四边形中,已知一边中点,由对称性画出其他三边的中点;将特殊四边形的四个中点呈“十字相连”,得到四个与原四边形相似的小的四边形,继续作这些小四边形的中点并呈“十字相连”,得到一个网格,每一个中点均是网格的格点,且该网格具有该特殊四边形的一切性质.
3.如图,△ABC的三个顶点分别在正方形网格的格点上,请按要求完成下列各题:
(1)在图①中找一格点D,连接BD,使∠ABD与∠BAC互补;
(2)在图②中找一格点E,连接BE,使∠ABE与∠BAC互余;
(3)在图③中找一格点F,连接BF,使∠ABF=45°.
【思路点拨】(1)作BD∥AC;(2)将(1)中BD旋转90°,或作BE⊥AC;(3)作等腰直角三角形ABF.
解:(1)如图①,点D即为所求.(2)如图②,点E 即为所求.(答案不唯一)(3)如图③,点F即为所求.
【方法归纳】无刻度直尺作图常考模型
模型一 特殊角问题
举例:在图①中,找一格点C,使∠BAC=45°(画出一种即可).
原理:由∠BAC=45°,可得以点B或点C为直角顶点的等腰三角形ABC,再结合点C为格点,即可画出符合要求的图形.
作答:∠BAC如图②所示.(答案不唯一,作出其中一种即可).
模型二 找中点或n等分点问题
举例:在图③中找出线段AB的中点P以及线段AB的一个离点B最近的四等分点Q.
原理:全等三角形对应边相等;相似三角形对应边成比例.
作答:点P如图④所示;点Q如图⑤所示.
模型三 面积相等问题
举例:在图⑥中找一格点E,使S△ABE=S△ABC.
原理:平行线间的距离相等.将固定的一边AB在网格中进行平移,直至经过点C,即可作出符合要求的格点图形.
作答:点E如图⑦所示.
4.在△ABC中,AB=AC,请仅用无刻度的直尺分别按下列要求画图(不写作法,只保留作图痕迹)
(1)点D,E分别是AB,AC的中点,在图①中画出BC边上的高线;
(2)BE⊥AC,CD⊥AB,在图②中画出∠BAC的平分线.
解:(1)如图①,AP即为所求.
(2)如图②,AG即为所求.
5.(2022·武汉)如图是由小正方形组成的9×6网格,每个小正方形的顶点叫做格点.△ABC的三个顶点都是格点.仅用无刻度的直尺在给定网格中完成画图,画图过程用虚线表示.
(1)在图①中,D,E分别是边AB,
AC与网格线的交点.先将点B绕
点E旋转180°得到点F,画出点F,
再在AC上画点G,使DG∥BC;
(2)在图②中,P是边AB上一点,∠BAC=α.先将AB绕点A逆时针旋转2α,得到线段AH,画出线段AH,再画点Q,使P,Q两点关于直线AC对称.
解:(1)作图如图①所示.
(2)作图如图②所示.
6.(2024·江西)如图,AC为菱形ABCD的对角线,请仅用无刻度的直尺按要求完成以下作图(保留作图痕迹)
(1)如图①,过点B作AC的垂线;
(2)如图②,点E为线段AB的中点,过点B作AC的平行线.
解:(1)如图所示,BD即为所求.
(2)如图所示,BM即为所求.
同课章节目录
