中考数学复习第三章函数第九节二次函数与几何综合课件
文档属性
| 名称 | 中考数学复习第三章函数第九节二次函数与几何综合课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 6.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:16:00 | ||
图片预览










文档简介
(共67张PPT)
类型一:二次函数与线段问题
[一题多角度]如图①,抛物线y=x2-3x-4与x轴交于A,B两点(点A在点B右侧),与y轴交于点C,P是第四象限内抛物线上一点,其横坐标为t.
【能力点一】 表示点的坐标
(1)点P的坐标可表示为 ;
(2)Q是抛物线对称轴上一点,其纵坐标为n,则点Q的坐标可表示为 ;
(3)点P关于抛物线对称轴对称的点的坐标可表示为 ;
(4)将抛物线向右平移3个单位长度,再向下平移4个单位长度,则点P的对应点P′的坐标可表示为 ;
(t,t2-3t-4)
(3-t,t2-3t-4)
(t+3,t2-3t-8)
【能力点二】 表示线段的长
(5)如图②,连接AC,过点P作x轴的垂线,交AC于点E,交x轴于点D.
Ⅰ)线段DE的长可表示为 ,线段PE的长可表示为 ;
Ⅱ)当点E为PD的中点时,PD的长为 ;
(6)如图③,过点P作PF⊥AC于点F,则PF的长可表示为 ;
【能力点三】 表示三角形的周长
(7)如图③,过点P作PF⊥AC于点F,△PEF的周长可表示为
.
4-t
-t2+4t
6
-t2+2t
-(1+)t2+4(1+)t
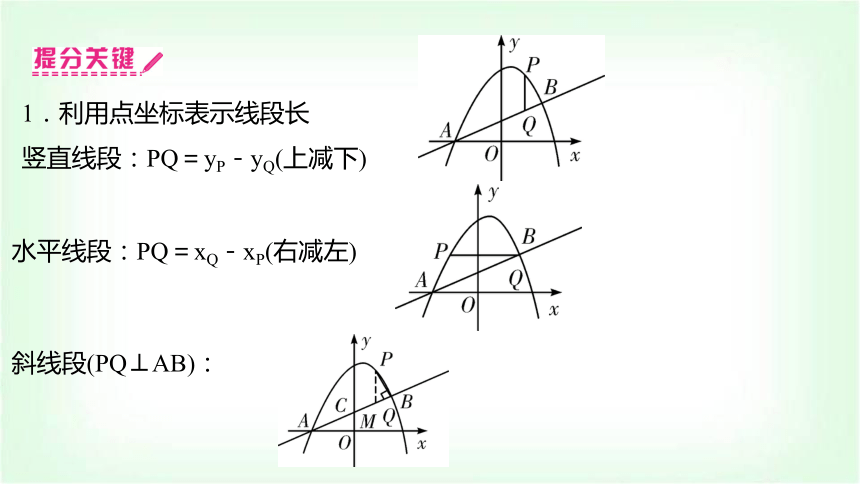
1.利用点坐标表示线段长
竖直线段:PQ=yP-yQ(上减下)
水平线段:PQ=xQ-xP(右减左)
斜线段(PQ⊥AB):
利用△PQM∽△AOC,将斜线段PQ转换成竖直线段PM.
求三角形周长时,一般先将斜线段转换成竖直或水平线段,然后相加.
2.利用直线位置关系表示线段长:若直线y1=k1x+b1与直线y2=k2x+b2平行,则k1=k2;若直线y1=k1x+b1与直线y2=k2x+b2垂直,则k1·k2=-1.再利用两点间距离公式求解即可.
[一题多角度]如图①,抛物线y=ax2-x+c与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线顶点坐标为(-2,4),P是位于直线AC上方抛物线上一点.
(1)求抛物线的解析式;
解:根据题意,得
解得
∴抛物线的解析式为y=-x2-x+3.
(2)如图②,过点P作PE∥x轴,交直线AC于点E,求PE的最大值;
【分层分析】由题意可知PE∥x轴,点E在点P的右侧,则PE的长表示为
xE-xP.以点P,E的纵坐标为纽带表示出xE,xP.
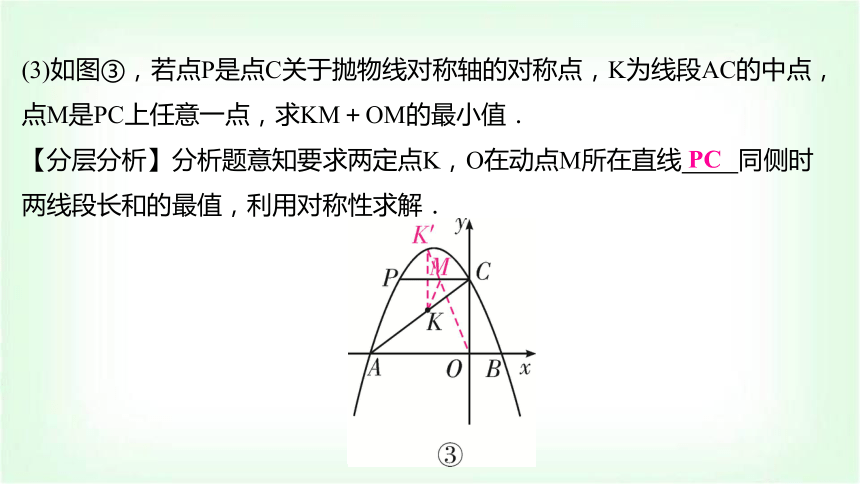
(3)如图③,若点P是点C关于抛物线对称轴的对称点,K为线段AC的中点,点M是PC上任意一点,求KM+OM的最小值.
【分层分析】分析题意知要求两定点K,O在动点M所在直线 同侧时两线段长和的最值,利用对称性求解.
PC
线段最值问题
(1)利用二次函数性质求最值:
①求竖直线段MN长的最大值(如图①′)
第一步:设点M(t,at2+bt+c),则N(t,mt+n);
第二步:表示线段MN的长, ①′
MN=at2+bt+c-mt-n;
第三步:化简MN=at2+bt+c-mt-n=at2+(b-m)t+c-n,利用二次函数性质求最值.
②′
②求斜线段MP长的最大值(如图②′)
利用锐角三角函数化斜为直得MP=MN·sin∠MNP,再根据①的步骤解题即可.
(2)利用两点之间线段最短求线段和最小值(如图③′,求|PA+PB|最小值):
①求点A关于对称轴l对称的点A′的坐标;
②连接A′B交直线l于点P′,此时点P满足要求;
③用待定系数法求直线A′B的函数解析式;
④将直线l对应的x的值代入直线A′B的函数解析式可得点P的坐标从而求出|PA+PB|的最小值
③′
(-1,0)
(3,0)
(1,2)
3
1
2-1
1
解法二 连接OD.
S△CDB=S△COD+S△DOB-S△BOC
= = .
(3)如图③,P是第一象限内抛物线上一动点,连接CP,PB,设点P的横坐标为p,请用含p的式子表示△BCP与四边形OCPB的面积.
如图①,已知抛物线y=ax2+bx-4与x轴交于A,B两点,与y轴交于点C,点A,B的坐标为(-2,0),(8,0),P是直线BC下方抛物线上一点.
(1)①抛物线的解析式为 ;
②直线BC的解析式为 ;
③S△ABC= ;
20
(2)补全法
S△ABC=S△ACD-S△ABD-S△BCD S△ABC=S矩形BDEF-S△ACE-S△BCD-S△ABF
(2)如图①,是否存在点P,使得S△PAB=S△ABC,若存在,请求出点P的坐标;若不存在,请说明理由;
解:存在,抛物线的对称轴为直线x=3,
∵S△PAB=S△ABC,∴△PAB与△ABC是同底等高,
∴点P与点C关于对称轴对称,∴P(6,-4).
(3)如图②,连接PB,PC,BC,求四边形PBAC面积的最大值及此时点P的坐标;
【分层分析】
通过观察可知,S四边形PBAC=S△PBC+S△ABC,而S△ABC=20.只需表示出S△PBC,而△PBC是三边均不与坐标轴平行的三角形,利用“分割法”或“补全法”进行求解即可.
【分层分析】
通过观察,以MP为底的△BPM和以AM为底的△ABM的高相同,则只需要表示出其底边之比即可根据函数性质求出面积之比的最大值.
类型三:二次函数与特殊三角形问题
如图,在平面直角坐标系中有一点P(4,3),连接OP,在x轴上找一点Q,使△OPQ是以OP为腰的等腰三角形,求点Q的坐标.
解:∵P(4,3),∴OP=5,设点Q的坐标为(m,0),则OQ=|m|.
①当OQ=OP,则|m|=5,∴m=±5;
②PO=PQ,过点P作PH⊥x轴于点H,
∴OH=QH=4,∴OQ=8,∴m=8.
综上所述,点Q的坐标为(-5,0),(5,0)或(8,0).
如图,已知A(2,1),B(4,3),C为坐标轴上的点,且使得△ABC是以AB为底边的等腰三角形.请求出点C的坐标.
解:若点C在x轴上,设点C的坐标为(x,0),
则AC=BC,
即(2-x)2+(1-0)2=(4-x)2+(3-0)2,
解得x=5,即点C的坐标为(5,0);
若点C在y轴上,设点C的坐标为(0,y),则AC=BC,即
(2-0)2+(1-y)2=(4-0)2+(3-y)2,
解得y=5,即点C的坐标为(0,5).
综上所述,点C的坐标为(5,0)或(0,5).
如图,在平面直角坐标系中,直线AB分别与x轴,y轴交于点A(3,0),
B(0,4),P为y轴上一点,当△PAB为直角三角形时,求点P的坐标.
1.确定等腰三角形第三点的方法:
“两圆一线”模型:已知线段AB,在平面内找一点C使得△ABC为等腰三角形,这样的点C位置有以下两种情况:
(1)以AB为腰:点C在分别以点A,B为圆心,
AB长为半径的圆上,AB直线上的点除外;
(2)以AB为底:点C在AB的垂直平分线上,
AB直线上的点除外.简称“两圆一线”.
2.确定直角三角形第三点的方法:
△ABC为直角三角形,A,B为定点,C为动点,确定点C的轨迹.
(1)若∠A=90°,过点A作AB的垂线,垂线l1
即为点C的轨迹(点A除外);
(2)若∠B=90°,过点B作AB的垂线,垂线l2
即为点C的轨迹(点B除外);
(3)若∠C=90°,以AB为直径作圆,所作圆
即为点C的轨迹(A,B两点除外).
简称“一圆两垂直”.作图如图所示.
抛物线y=x2-2x-3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.
(1)如图①,连接AC,在抛物线的对称轴上,是否存在点P,使得△PAC是等腰三角形.若存在,求出点P的坐标;
若不存在,请说明理由;
【分层分析】利用两圆一中垂的方法在直线l上
找出点P,共有5个,并注意检验点P是否满足条件,
当点P,A,C共线时,不符合题意.
(2)如图②,连接AC,在抛物线的对称轴l上,是否存在点P,使△PAC为直角三角形,若存在,求出点P的坐标;若不存在,请说明理由;
【分层分析】按照直角三角形找点方法,过点A作AP1⊥AC交直线l于点
P1,过点C作CP2⊥AC交直线l于点P2;以AC为直径作圆,与直线l交于点P3,P4,再用相似,三角函数,勾股定理或解析法列方程求解.
类型四:二次函数与特殊四边形问题
解:当BC∥DA,BC=DA时,A和D的纵坐标相等,
BC之间的距离为4-0=4.
当D在A左边时(如图①),横坐标为3-4=-1,
此时D点坐标为(-1,2);
如图,在平面直角坐标系中,已知A(3,2),B(0,0),C(4,0),在平面坐标系内找一点D,使这四点构成一个平行四边形.
当D在A右边时(如图②),横坐标为3+4=7,此时D点坐标为(7,2);
当AC∥DB,AC=BD时(如图③),由点A平移到点C是横坐标加1,纵坐标减2,那么由点B平移到点D也应如此移动:0+1=1,0-2=-2,
故此时D点坐标为(1,-2).
综上所述,点D的坐标为(7,2),(-1,2)或(1,-2).
如图,在平面直角坐标系中,已知点A(4,2),点B(-1,-3),P为x轴上一点,Q为y轴上一点.若要使以A,B,P,Q为顶点的四边形是平行四边形,求点P和点Q的坐标.
解:当AB为边,①即当四边形ABQ2P2是平行
四边形,则AB=P2Q2,AP2=BQ2,
∵点A(4,2),点B(-1,-3),
∴AB=5,则OP2=OQ2=5,
∴点Q2的坐标是(0,-5),点P2的坐标是(5,0);
②当四边形QPBA是平行四边形,
∴AB=PQ,QA=PB,
∴点Q的坐标是(0,5),点P的坐标是(-5,0);
③当AB为对角线,即当四边形P1AQ1B是平行四边形,
∴AP1=Q1B,AQ1=BP1,
∴点Q1的坐标是(0,-1),点P1的坐标是(3,0),
综上所述,点P的坐标为(5,0),(-5,0)或(3,0).
对应点Q的坐标为(0,-5),(0,5)或(0,-1).
1.平行四边形找点的方法:
(1)三定一动
构造已知边的对边,平行且等于已知边,确定第四个点.
(2)两定两动分两种情况讨论:
①若AB为平行四边形的边,将AB上下
左右平移,确定P,Q的位置;
②若AB为平行四边形的对角线,取AB中点,
旋转经过中点的直线确定P,Q的位置.
2.求点的坐标的常用方法:
(1)对边水平距离相等和竖直距离相等(平移)
(2)对角线互相平分
(3)矩形、菱形、正方形求解在平行四边形的基础上,再加条件.
在平面直角坐标系中,已知抛物线 y=-x2+x+2与x轴交于A,B两点,与y轴交于点C.
(1)如图,若点W在抛物线上,点D在y轴上,且四边形ADBW为平行四边形,求点D的坐标;
【分层分析】取AB的中点为T,
则点T的坐标为 (1,0),作WG⊥x轴于点G.
则GT=OT=1,求出点W.进而求出点D.
解:连接DW,取AB的中点为T,
则点T的坐标为(1,0),
作WG⊥x轴于点G,
则△OTD≌△GTW,
∴OT=GT=1,
将x=2代入y=-x2+x+2,得y=2,
∴点D的坐标为(0,-2).
(2)设点G是抛物线的对称轴上一点,H是坐标平面内一点,是否存在点G,使得以B,C,G,H为顶点的四边形是矩形,若存在,求出点G的坐标;若不存在,请说明理由;
【分层分析】要使以B,C,G,H为顶点的
四边形是矩形,只需△BCG是直角三角形即可,
可分为①∠BCG=90°;②∠CBG=90°;
③∠CGB=90°三种情况,分别利用勾股定理
列方程即可求解.
(3)设点Q是y轴上的动点,在坐标平面内是否存在点I,使得以点A,C,Q,I为顶点的四边形是菱形?若存在,请求出点I的坐标;若不存在,请说明理由.
【分层分析】以AC为对角线与以AC为边分
情况考虑构造平行四边形,利用菱形每边相
等及对边平行的性质,对每种情况进行讨论,
①若AC是菱形的对角线,结合勾股定理可求
出点Q坐标,利用中点坐标公式即可求出点I坐标.
②若AC是菱形的边,可结合图象,根据点的平移求出点I坐标.
类型五:二次函数与角度问题
1.如图,在平面直角坐标系中,点B的坐标为(1,0),AB⊥x轴于点B,若∠AOB=30°,则点A的坐标为 .
4.如图,在平面直角坐标系中,点A的坐标为(2,3),过点A作AB⊥x轴于点B,C是y轴上一动点,当∠ACO=∠AOB时,点C的坐标为
.
5.如图,在平面直角坐标系中,A(0,2),B(2,0),点P的坐标为(n,0),当∠PAB=15°时,点P的坐标为 .
6.如图,在平面直角坐标系中,已知点A的坐标为(2,3),过点A作
AB⊥x轴于点B,点C为x轴下方一点,当∠AOC=∠AOB+45°,且OA=OC时,点C的坐标为 .
1.(1)若所求角度为非特殊角,可通过相关角的和差关系将所求的角度转化为特殊角,再结合锐角三角函数求解;
(2)若探究角度之间的等量关系,常考虑将角放在直角三角形中,通过解直角三角形求解;
(3)若探究角度和为90°,一般可先画出符合条件的圆,通过圆的基本性质将角度进行转化求解.
2.若探索角度之间的关系:
(1)当两角相等时,可考虑构造角平分线求解,结合角平分线的解析式求解;
(2)当两角存在倍分关系时,考虑构造垂直平分线,结合垂直平分线的解析式求解;
(3)当一个角等于另一个角加上45°时,可考虑构造平行线,结合平行线的解析式求解.
抛物线y=-x2-2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D,连接AC,BC.
(1)如图①,直线AD与直线BC相交于点H,求∠ACD与∠AHB的度数;
(2)P是抛物线第二象限内一点,当CA平分∠OCP时,求点P的坐标;【分层分析】
当CA平分∠OCP时,CP∥AB,根据对称可求点P的坐标.
解:∵∠CAO=∠ACO=45°,CA平分∠OCP,∴∠OCP=90°,
∴CP∥AB,故点C与点P关于抛物线的对称轴对称,
又∵点C的坐标为(0,3),∴点P的坐标为(-2,3).
(3)如图②,过点A作射线AE交直线AC下方的抛物线于点E,使∠DAE=45°,求点E的坐标;
(4)如图③,点P在第二象限内的抛物线上,PG⊥x轴于点G,当∠GPB=
2∠BCO时,求点P的坐标.
【分层分析】设BP交y轴于点E,当∠GPB=2∠BCO时,则∠OEB=
2∠BCO,CE=EB.求出点E的坐标,从而求出直线PB的解析式,联解即可.
类型一:二次函数与线段问题
[一题多角度]如图①,抛物线y=x2-3x-4与x轴交于A,B两点(点A在点B右侧),与y轴交于点C,P是第四象限内抛物线上一点,其横坐标为t.
【能力点一】 表示点的坐标
(1)点P的坐标可表示为 ;
(2)Q是抛物线对称轴上一点,其纵坐标为n,则点Q的坐标可表示为 ;
(3)点P关于抛物线对称轴对称的点的坐标可表示为 ;
(4)将抛物线向右平移3个单位长度,再向下平移4个单位长度,则点P的对应点P′的坐标可表示为 ;
(t,t2-3t-4)
(3-t,t2-3t-4)
(t+3,t2-3t-8)
【能力点二】 表示线段的长
(5)如图②,连接AC,过点P作x轴的垂线,交AC于点E,交x轴于点D.
Ⅰ)线段DE的长可表示为 ,线段PE的长可表示为 ;
Ⅱ)当点E为PD的中点时,PD的长为 ;
(6)如图③,过点P作PF⊥AC于点F,则PF的长可表示为 ;
【能力点三】 表示三角形的周长
(7)如图③,过点P作PF⊥AC于点F,△PEF的周长可表示为
.
4-t
-t2+4t
6
-t2+2t
-(1+)t2+4(1+)t
1.利用点坐标表示线段长
竖直线段:PQ=yP-yQ(上减下)
水平线段:PQ=xQ-xP(右减左)
斜线段(PQ⊥AB):
利用△PQM∽△AOC,将斜线段PQ转换成竖直线段PM.
求三角形周长时,一般先将斜线段转换成竖直或水平线段,然后相加.
2.利用直线位置关系表示线段长:若直线y1=k1x+b1与直线y2=k2x+b2平行,则k1=k2;若直线y1=k1x+b1与直线y2=k2x+b2垂直,则k1·k2=-1.再利用两点间距离公式求解即可.
[一题多角度]如图①,抛物线y=ax2-x+c与x轴交于点A,B(点A在点B左侧),与y轴交于点C,抛物线顶点坐标为(-2,4),P是位于直线AC上方抛物线上一点.
(1)求抛物线的解析式;
解:根据题意,得
解得
∴抛物线的解析式为y=-x2-x+3.
(2)如图②,过点P作PE∥x轴,交直线AC于点E,求PE的最大值;
【分层分析】由题意可知PE∥x轴,点E在点P的右侧,则PE的长表示为
xE-xP.以点P,E的纵坐标为纽带表示出xE,xP.
(3)如图③,若点P是点C关于抛物线对称轴的对称点,K为线段AC的中点,点M是PC上任意一点,求KM+OM的最小值.
【分层分析】分析题意知要求两定点K,O在动点M所在直线 同侧时两线段长和的最值,利用对称性求解.
PC
线段最值问题
(1)利用二次函数性质求最值:
①求竖直线段MN长的最大值(如图①′)
第一步:设点M(t,at2+bt+c),则N(t,mt+n);
第二步:表示线段MN的长, ①′
MN=at2+bt+c-mt-n;
第三步:化简MN=at2+bt+c-mt-n=at2+(b-m)t+c-n,利用二次函数性质求最值.
②′
②求斜线段MP长的最大值(如图②′)
利用锐角三角函数化斜为直得MP=MN·sin∠MNP,再根据①的步骤解题即可.
(2)利用两点之间线段最短求线段和最小值(如图③′,求|PA+PB|最小值):
①求点A关于对称轴l对称的点A′的坐标;
②连接A′B交直线l于点P′,此时点P满足要求;
③用待定系数法求直线A′B的函数解析式;
④将直线l对应的x的值代入直线A′B的函数解析式可得点P的坐标从而求出|PA+PB|的最小值
③′
(-1,0)
(3,0)
(1,2)
3
1
2-1
1
解法二 连接OD.
S△CDB=S△COD+S△DOB-S△BOC
= = .
(3)如图③,P是第一象限内抛物线上一动点,连接CP,PB,设点P的横坐标为p,请用含p的式子表示△BCP与四边形OCPB的面积.
如图①,已知抛物线y=ax2+bx-4与x轴交于A,B两点,与y轴交于点C,点A,B的坐标为(-2,0),(8,0),P是直线BC下方抛物线上一点.
(1)①抛物线的解析式为 ;
②直线BC的解析式为 ;
③S△ABC= ;
20
(2)补全法
S△ABC=S△ACD-S△ABD-S△BCD S△ABC=S矩形BDEF-S△ACE-S△BCD-S△ABF
(2)如图①,是否存在点P,使得S△PAB=S△ABC,若存在,请求出点P的坐标;若不存在,请说明理由;
解:存在,抛物线的对称轴为直线x=3,
∵S△PAB=S△ABC,∴△PAB与△ABC是同底等高,
∴点P与点C关于对称轴对称,∴P(6,-4).
(3)如图②,连接PB,PC,BC,求四边形PBAC面积的最大值及此时点P的坐标;
【分层分析】
通过观察可知,S四边形PBAC=S△PBC+S△ABC,而S△ABC=20.只需表示出S△PBC,而△PBC是三边均不与坐标轴平行的三角形,利用“分割法”或“补全法”进行求解即可.
【分层分析】
通过观察,以MP为底的△BPM和以AM为底的△ABM的高相同,则只需要表示出其底边之比即可根据函数性质求出面积之比的最大值.
类型三:二次函数与特殊三角形问题
如图,在平面直角坐标系中有一点P(4,3),连接OP,在x轴上找一点Q,使△OPQ是以OP为腰的等腰三角形,求点Q的坐标.
解:∵P(4,3),∴OP=5,设点Q的坐标为(m,0),则OQ=|m|.
①当OQ=OP,则|m|=5,∴m=±5;
②PO=PQ,过点P作PH⊥x轴于点H,
∴OH=QH=4,∴OQ=8,∴m=8.
综上所述,点Q的坐标为(-5,0),(5,0)或(8,0).
如图,已知A(2,1),B(4,3),C为坐标轴上的点,且使得△ABC是以AB为底边的等腰三角形.请求出点C的坐标.
解:若点C在x轴上,设点C的坐标为(x,0),
则AC=BC,
即(2-x)2+(1-0)2=(4-x)2+(3-0)2,
解得x=5,即点C的坐标为(5,0);
若点C在y轴上,设点C的坐标为(0,y),则AC=BC,即
(2-0)2+(1-y)2=(4-0)2+(3-y)2,
解得y=5,即点C的坐标为(0,5).
综上所述,点C的坐标为(5,0)或(0,5).
如图,在平面直角坐标系中,直线AB分别与x轴,y轴交于点A(3,0),
B(0,4),P为y轴上一点,当△PAB为直角三角形时,求点P的坐标.
1.确定等腰三角形第三点的方法:
“两圆一线”模型:已知线段AB,在平面内找一点C使得△ABC为等腰三角形,这样的点C位置有以下两种情况:
(1)以AB为腰:点C在分别以点A,B为圆心,
AB长为半径的圆上,AB直线上的点除外;
(2)以AB为底:点C在AB的垂直平分线上,
AB直线上的点除外.简称“两圆一线”.
2.确定直角三角形第三点的方法:
△ABC为直角三角形,A,B为定点,C为动点,确定点C的轨迹.
(1)若∠A=90°,过点A作AB的垂线,垂线l1
即为点C的轨迹(点A除外);
(2)若∠B=90°,过点B作AB的垂线,垂线l2
即为点C的轨迹(点B除外);
(3)若∠C=90°,以AB为直径作圆,所作圆
即为点C的轨迹(A,B两点除外).
简称“一圆两垂直”.作图如图所示.
抛物线y=x2-2x-3与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,对称轴为直线l.
(1)如图①,连接AC,在抛物线的对称轴上,是否存在点P,使得△PAC是等腰三角形.若存在,求出点P的坐标;
若不存在,请说明理由;
【分层分析】利用两圆一中垂的方法在直线l上
找出点P,共有5个,并注意检验点P是否满足条件,
当点P,A,C共线时,不符合题意.
(2)如图②,连接AC,在抛物线的对称轴l上,是否存在点P,使△PAC为直角三角形,若存在,求出点P的坐标;若不存在,请说明理由;
【分层分析】按照直角三角形找点方法,过点A作AP1⊥AC交直线l于点
P1,过点C作CP2⊥AC交直线l于点P2;以AC为直径作圆,与直线l交于点P3,P4,再用相似,三角函数,勾股定理或解析法列方程求解.
类型四:二次函数与特殊四边形问题
解:当BC∥DA,BC=DA时,A和D的纵坐标相等,
BC之间的距离为4-0=4.
当D在A左边时(如图①),横坐标为3-4=-1,
此时D点坐标为(-1,2);
如图,在平面直角坐标系中,已知A(3,2),B(0,0),C(4,0),在平面坐标系内找一点D,使这四点构成一个平行四边形.
当D在A右边时(如图②),横坐标为3+4=7,此时D点坐标为(7,2);
当AC∥DB,AC=BD时(如图③),由点A平移到点C是横坐标加1,纵坐标减2,那么由点B平移到点D也应如此移动:0+1=1,0-2=-2,
故此时D点坐标为(1,-2).
综上所述,点D的坐标为(7,2),(-1,2)或(1,-2).
如图,在平面直角坐标系中,已知点A(4,2),点B(-1,-3),P为x轴上一点,Q为y轴上一点.若要使以A,B,P,Q为顶点的四边形是平行四边形,求点P和点Q的坐标.
解:当AB为边,①即当四边形ABQ2P2是平行
四边形,则AB=P2Q2,AP2=BQ2,
∵点A(4,2),点B(-1,-3),
∴AB=5,则OP2=OQ2=5,
∴点Q2的坐标是(0,-5),点P2的坐标是(5,0);
②当四边形QPBA是平行四边形,
∴AB=PQ,QA=PB,
∴点Q的坐标是(0,5),点P的坐标是(-5,0);
③当AB为对角线,即当四边形P1AQ1B是平行四边形,
∴AP1=Q1B,AQ1=BP1,
∴点Q1的坐标是(0,-1),点P1的坐标是(3,0),
综上所述,点P的坐标为(5,0),(-5,0)或(3,0).
对应点Q的坐标为(0,-5),(0,5)或(0,-1).
1.平行四边形找点的方法:
(1)三定一动
构造已知边的对边,平行且等于已知边,确定第四个点.
(2)两定两动分两种情况讨论:
①若AB为平行四边形的边,将AB上下
左右平移,确定P,Q的位置;
②若AB为平行四边形的对角线,取AB中点,
旋转经过中点的直线确定P,Q的位置.
2.求点的坐标的常用方法:
(1)对边水平距离相等和竖直距离相等(平移)
(2)对角线互相平分
(3)矩形、菱形、正方形求解在平行四边形的基础上,再加条件.
在平面直角坐标系中,已知抛物线 y=-x2+x+2与x轴交于A,B两点,与y轴交于点C.
(1)如图,若点W在抛物线上,点D在y轴上,且四边形ADBW为平行四边形,求点D的坐标;
【分层分析】取AB的中点为T,
则点T的坐标为 (1,0),作WG⊥x轴于点G.
则GT=OT=1,求出点W.进而求出点D.
解:连接DW,取AB的中点为T,
则点T的坐标为(1,0),
作WG⊥x轴于点G,
则△OTD≌△GTW,
∴OT=GT=1,
将x=2代入y=-x2+x+2,得y=2,
∴点D的坐标为(0,-2).
(2)设点G是抛物线的对称轴上一点,H是坐标平面内一点,是否存在点G,使得以B,C,G,H为顶点的四边形是矩形,若存在,求出点G的坐标;若不存在,请说明理由;
【分层分析】要使以B,C,G,H为顶点的
四边形是矩形,只需△BCG是直角三角形即可,
可分为①∠BCG=90°;②∠CBG=90°;
③∠CGB=90°三种情况,分别利用勾股定理
列方程即可求解.
(3)设点Q是y轴上的动点,在坐标平面内是否存在点I,使得以点A,C,Q,I为顶点的四边形是菱形?若存在,请求出点I的坐标;若不存在,请说明理由.
【分层分析】以AC为对角线与以AC为边分
情况考虑构造平行四边形,利用菱形每边相
等及对边平行的性质,对每种情况进行讨论,
①若AC是菱形的对角线,结合勾股定理可求
出点Q坐标,利用中点坐标公式即可求出点I坐标.
②若AC是菱形的边,可结合图象,根据点的平移求出点I坐标.
类型五:二次函数与角度问题
1.如图,在平面直角坐标系中,点B的坐标为(1,0),AB⊥x轴于点B,若∠AOB=30°,则点A的坐标为 .
4.如图,在平面直角坐标系中,点A的坐标为(2,3),过点A作AB⊥x轴于点B,C是y轴上一动点,当∠ACO=∠AOB时,点C的坐标为
.
5.如图,在平面直角坐标系中,A(0,2),B(2,0),点P的坐标为(n,0),当∠PAB=15°时,点P的坐标为 .
6.如图,在平面直角坐标系中,已知点A的坐标为(2,3),过点A作
AB⊥x轴于点B,点C为x轴下方一点,当∠AOC=∠AOB+45°,且OA=OC时,点C的坐标为 .
1.(1)若所求角度为非特殊角,可通过相关角的和差关系将所求的角度转化为特殊角,再结合锐角三角函数求解;
(2)若探究角度之间的等量关系,常考虑将角放在直角三角形中,通过解直角三角形求解;
(3)若探究角度和为90°,一般可先画出符合条件的圆,通过圆的基本性质将角度进行转化求解.
2.若探索角度之间的关系:
(1)当两角相等时,可考虑构造角平分线求解,结合角平分线的解析式求解;
(2)当两角存在倍分关系时,考虑构造垂直平分线,结合垂直平分线的解析式求解;
(3)当一个角等于另一个角加上45°时,可考虑构造平行线,结合平行线的解析式求解.
抛物线y=-x2-2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,顶点为D,连接AC,BC.
(1)如图①,直线AD与直线BC相交于点H,求∠ACD与∠AHB的度数;
(2)P是抛物线第二象限内一点,当CA平分∠OCP时,求点P的坐标;【分层分析】
当CA平分∠OCP时,CP∥AB,根据对称可求点P的坐标.
解:∵∠CAO=∠ACO=45°,CA平分∠OCP,∴∠OCP=90°,
∴CP∥AB,故点C与点P关于抛物线的对称轴对称,
又∵点C的坐标为(0,3),∴点P的坐标为(-2,3).
(3)如图②,过点A作射线AE交直线AC下方的抛物线于点E,使∠DAE=45°,求点E的坐标;
(4)如图③,点P在第二象限内的抛物线上,PG⊥x轴于点G,当∠GPB=
2∠BCO时,求点P的坐标.
【分层分析】设BP交y轴于点E,当∠GPB=2∠BCO时,则∠OEB=
2∠BCO,CE=EB.求出点E的坐标,从而求出直线PB的解析式,联解即可.
同课章节目录
