中考数学复习第三章函数微专题(二)二次函数的区间最值问题课件
文档属性
| 名称 | 中考数学复习第三章函数微专题(二)二次函数的区间最值问题课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 780.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:16:00 | ||
图片预览






文档简介
(共14张PPT)
考向1 求确定区间的最值
[一题多角度]已知二次函数y=2x2-4x-6,配方化为顶点式为
,对称轴为 ,当 时,y随x的增大而增大.
(1)当-1≤x≤0时,二次函数的最大值是 ,最小值是 ;
(2)当2≤x≤5时,二次函数的最大值是 ,最小值是 ;
(3)当-3≤x≤2时,y的取值范围是 ;
y=2(x-1)2-8
直线x=1
x≥1
0
-6
24
-6
-8≤y≤24
考向2 解析式确定,区间不确定
[一题多角度]求二次函数y=x2+2x-3在k≤x≤k+2上的最大值和最小值.
(1)若区间在对称轴左侧(如图①):
当 ,即k 时;
当x=k+2时,y有最小值,y最小= ;
当x=k时,y有最大值,y最大= .
k+2≤-1
≤-3
k2+6k+5
k2+2k-3
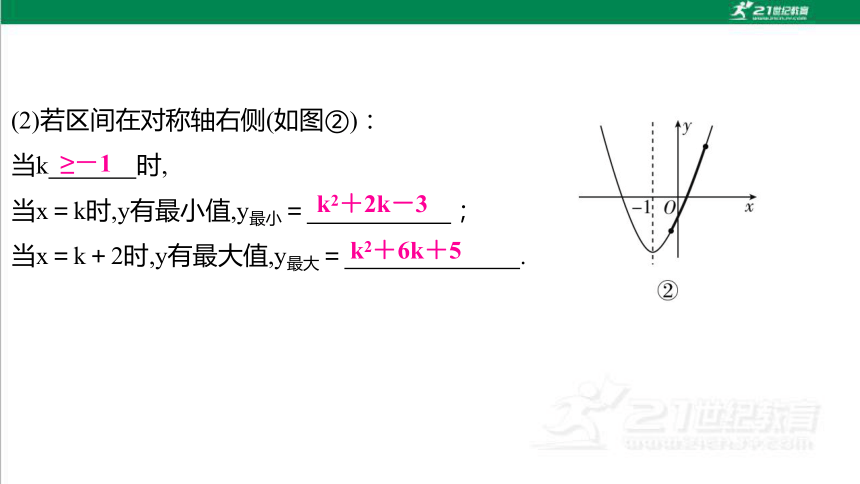
(2)若区间在对称轴右侧(如图②):
当k 时,
当x=k时,y有最小值,y最小= ;
当x=k+2时,y有最大值,y最大= .
≥-1
k2+2k-3
k2+6k+5
(3)若对称轴在区间之间(如图③):
①区间中轴线(直线x=k+1)在对称轴右侧:
当 时,
y最小= ;y最大= .
-2<k≤-1
-4
k2+6k+5
②区间中轴线(直线x=k+1)在对称轴左侧(如图④):
当 时,
y最小= ;y最大= .
-3≤k<-2
-4
k2+2k-3
考向3 解析式不确定,区间确定
若-1≤x≤1,求函数y=x2+2ax+3的最大值和最小值.
(1)若对称轴在区间左侧(如图⑤):
当 时,函数在-1≤x≤1的区间内,y随x的增大而增大;
当x=-1时,函数有最小值,y最小= ;
当x=1时,函数有最大值,y最大= .
a>1
4-2a
4+2a
(2)若对称轴在区间右侧(如图⑥):
当 时,函数在-1≤x≤1区间内,y随x的增大而减小;
当x=1时,函数有最小值,y最小= ;
当x=-1时,函数有最大值,y最大= .
a<-1
4+2a
4-2a
(3)若对称轴在区间中间:
①对称轴在区间中轴线(即y轴)左侧:
当 时,函数在-1≤x≤1区间内(如图⑦);
当x=-a时,函数有最小值,y最小= ;
当x=1时,函数有最大值,y最大= .
0<a≤1
3-a2
4+2a
②对称轴在区间中轴线(即y轴)右侧(如图⑧):
当 时,函数在-1≤x≤1区间内;
当x=-a时,函数有最小值,y最小= ;
当x=-1时,函数有最大值,y最大= .
-1≤a<0
3-a2
4-2a
[一题多角度]已知抛物线y=2x2-4nx+2n2+1.
(1)当-2≤x≤1时,函数的最小值为3,求n的值;
解:y=2x2-4nx+2n2+1=2(x-n)2+1,
∵-2≤x≤1时函数的最小值为3,
∴当n≤-2时,-2≤x≤1在对称轴右侧,
y随x的增大而增大,当x=-2时,y最小=3.
即2(-2-n)2+1=3,解得n1=-1,n2=-3,
∵n≤-2,∴n=-3;
当n≥1时,-2≤x≤1在对称轴左侧,
y随x的增大而减小,
当x=1时,y最小=3,即2(1-n)2+1=3,
解得n=0或n=2,
∵n≥1,∴n=2.
综上所述,n的值为-3或2.
(2)当x≤2n时,函数的最小值为3,求n的值.
解:∵当x=n时,最小值为1,而x≤2n时,最小值为3,要分两种情况,
当2ny随x的增大而减小,当x=2n时,y最小=3,
即2(2n-n)2+1=3,n=±1.∵n<0,∴n=-1;
当2n>n,即n>0时,对称轴x=n满足区间x≤2n,此时最小值为1,不成立.
综上所述,n的值为-1.
考向1 求确定区间的最值
[一题多角度]已知二次函数y=2x2-4x-6,配方化为顶点式为
,对称轴为 ,当 时,y随x的增大而增大.
(1)当-1≤x≤0时,二次函数的最大值是 ,最小值是 ;
(2)当2≤x≤5时,二次函数的最大值是 ,最小值是 ;
(3)当-3≤x≤2时,y的取值范围是 ;
y=2(x-1)2-8
直线x=1
x≥1
0
-6
24
-6
-8≤y≤24
考向2 解析式确定,区间不确定
[一题多角度]求二次函数y=x2+2x-3在k≤x≤k+2上的最大值和最小值.
(1)若区间在对称轴左侧(如图①):
当 ,即k 时;
当x=k+2时,y有最小值,y最小= ;
当x=k时,y有最大值,y最大= .
k+2≤-1
≤-3
k2+6k+5
k2+2k-3
(2)若区间在对称轴右侧(如图②):
当k 时,
当x=k时,y有最小值,y最小= ;
当x=k+2时,y有最大值,y最大= .
≥-1
k2+2k-3
k2+6k+5
(3)若对称轴在区间之间(如图③):
①区间中轴线(直线x=k+1)在对称轴右侧:
当 时,
y最小= ;y最大= .
-2<k≤-1
-4
k2+6k+5
②区间中轴线(直线x=k+1)在对称轴左侧(如图④):
当 时,
y最小= ;y最大= .
-3≤k<-2
-4
k2+2k-3
考向3 解析式不确定,区间确定
若-1≤x≤1,求函数y=x2+2ax+3的最大值和最小值.
(1)若对称轴在区间左侧(如图⑤):
当 时,函数在-1≤x≤1的区间内,y随x的增大而增大;
当x=-1时,函数有最小值,y最小= ;
当x=1时,函数有最大值,y最大= .
a>1
4-2a
4+2a
(2)若对称轴在区间右侧(如图⑥):
当 时,函数在-1≤x≤1区间内,y随x的增大而减小;
当x=1时,函数有最小值,y最小= ;
当x=-1时,函数有最大值,y最大= .
a<-1
4+2a
4-2a
(3)若对称轴在区间中间:
①对称轴在区间中轴线(即y轴)左侧:
当 时,函数在-1≤x≤1区间内(如图⑦);
当x=-a时,函数有最小值,y最小= ;
当x=1时,函数有最大值,y最大= .
0<a≤1
3-a2
4+2a
②对称轴在区间中轴线(即y轴)右侧(如图⑧):
当 时,函数在-1≤x≤1区间内;
当x=-a时,函数有最小值,y最小= ;
当x=-1时,函数有最大值,y最大= .
-1≤a<0
3-a2
4-2a
[一题多角度]已知抛物线y=2x2-4nx+2n2+1.
(1)当-2≤x≤1时,函数的最小值为3,求n的值;
解:y=2x2-4nx+2n2+1=2(x-n)2+1,
∵-2≤x≤1时函数的最小值为3,
∴当n≤-2时,-2≤x≤1在对称轴右侧,
y随x的增大而增大,当x=-2时,y最小=3.
即2(-2-n)2+1=3,解得n1=-1,n2=-3,
∵n≤-2,∴n=-3;
当n≥1时,-2≤x≤1在对称轴左侧,
y随x的增大而减小,
当x=1时,y最小=3,即2(1-n)2+1=3,
解得n=0或n=2,
∵n≥1,∴n=2.
综上所述,n的值为-3或2.
(2)当x≤2n时,函数的最小值为3,求n的值.
解:∵当x=n时,最小值为1,而x≤2n时,最小值为3,要分两种情况,
当2n
即2(2n-n)2+1=3,n=±1.∵n<0,∴n=-1;
当2n>n,即n>0时,对称轴x=n满足区间x≤2n,此时最小值为1,不成立.
综上所述,n的值为-1.
同课章节目录
