中考数学复习第三章函数第八节二次函数的实际应用课件
文档属性
| 名称 | 中考数学复习第三章函数第八节二次函数的实际应用课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
二次函数的实际应用
二次函数的实际应用
二次函数的实际应用
1.为方便市民进行垃圾分类投放,某环保公司第一个月投放a个垃圾桶,计划第三个月投放垃圾桶y个,设该公司第二、三两个月投放垃圾桶数量的月平均增长率为x,那么y与x的函数关系是 .
2.(1)某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500 kg;销售单价每涨2元,月销售量就减少10 kg.设每千克涨x元,月销售利润为y元,则y与x的函数关系式为 ;
(2)某商场降价销售一批名牌衬衫,已知所获利润y(单位:元)与降价x(单位:元)之间的关系是 y=-2x2+60x+800,则利润获得最多为 元.
y=a(1+x)2
y=-5x2+450x+5 000
1 250
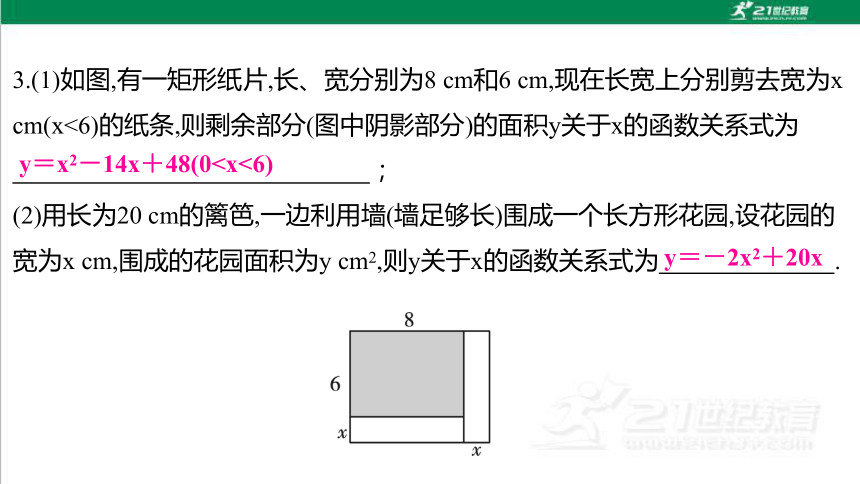
3.(1)如图,有一矩形纸片,长、宽分别为8 cm和6 cm,现在长宽上分别剪去宽为x cm(x<6)的纸条,则剩余部分(图中阴影部分)的面积y关于x的函数关系式为
;
(2)用长为20 cm的篱笆,一边利用墙(墙足够长)围成一个长方形花园,设花园的宽为x cm,围成的花园面积为y cm2,则y关于x的函数关系式为 .
y=x2-14x+48(0y=-2x2+20x
3
14
(2)求玩具每天的销售利润w(单位:元)与售价x(单位:元)之间的函数关系式;
解:w=(x-10)(-10x+300)
=-10x2+400x-3 000.
(3)该商场为了让利给顾客,且每天获得750元利润,售价应定为多少?
解:要使w=750,即-10x2+400x-3 000=750,
解得x1=15,x2=25,
∵要让利给顾客,∴x=15.
答:为了让利给顾客,且每天获利750元,售价应定为15元/个.
【方法归纳】此类问题一般涉及抛球、投篮、隧道、拱桥、喷泉水柱等,解决此类问题的关键是理解题目中的条件所表示的几何意义.最高点为抛物线的顶点,抛出点为抛物线中的c值,落地点为抛物线与x轴的交点,落地点到抛出点的水平距离是此落地点横坐标的绝对值.
(1)抛球运动判断球是否过网即判断此点的坐标是否在抛物线上方;
(2)投篮判断是否能投中即判断篮网是否在球的运动轨迹所在的抛物线上;
(3)判断车是否能通过隧道即判断车顶两端点的坐标是否在抛物线的下方;
(4)判断船是否能通过拱桥即判断船两端的高度是否比桥上对应点到水面的距离小;
(5)判断人是否会被喷泉淋湿即判断人所处位置的水的高度是否比人的身高要高.
【分层分析】(1)将点A坐标代入解析式可求a,即可求解;
(2)先画出能接到沙包的示意图,再根据点A的取值范围代入解析式可求解.
类型3:利用二次函数解决围栏面积问题
如图,某农户计划用篱笆围成一个矩形场地养殖家禽,为充分利用现有资源,该矩形场地一面靠墙(墙的长度为18 m),另外三面用篱笆围成,中间再用篱笆把它分成三个面积相等的矩形分别养殖不同的家禽,计划购买篱笆的总长度为 32 m,设矩形场地的长为x m, 宽为y m, 面积为S m2.
(1)分别求出y与x,S与x的函数解析式;
(2)当x为何值时,矩形场地的总面积最大?
最大面积为多少?
(1)求点A的坐标;
(2)求该抛物线的函数解析式;
(3)求起跳点A与着陆坡顶端C之间的水平距离OC的长.
(结果精确到0.1 m,参考数据:≈1.73)
解:(1)∵OA=4,且点A在y轴正半轴,∴A(0,4).
2.(2024·贵州)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(单位:盒)与销售单价x(单位:元)是一次函数关系,下表是y与x的几组对应值.
(1)求y与x的函数解析式;
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
解:(1)y与x的函数解析式为y=-2x+80.
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
解:(2)设日销售利润为w元,根据题意,得
w=(x-10)·y=(x-10)(-2x+80)
=-2(x-25)2+450,
∴当x=25时,w有最大值为450,
∴糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元.
3)若超市决定每销售一盒糖果便向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
二次函数的实际应用
二次函数的实际应用
二次函数的实际应用
1.为方便市民进行垃圾分类投放,某环保公司第一个月投放a个垃圾桶,计划第三个月投放垃圾桶y个,设该公司第二、三两个月投放垃圾桶数量的月平均增长率为x,那么y与x的函数关系是 .
2.(1)某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500 kg;销售单价每涨2元,月销售量就减少10 kg.设每千克涨x元,月销售利润为y元,则y与x的函数关系式为 ;
(2)某商场降价销售一批名牌衬衫,已知所获利润y(单位:元)与降价x(单位:元)之间的关系是 y=-2x2+60x+800,则利润获得最多为 元.
y=a(1+x)2
y=-5x2+450x+5 000
1 250
3.(1)如图,有一矩形纸片,长、宽分别为8 cm和6 cm,现在长宽上分别剪去宽为x cm(x<6)的纸条,则剩余部分(图中阴影部分)的面积y关于x的函数关系式为
;
(2)用长为20 cm的篱笆,一边利用墙(墙足够长)围成一个长方形花园,设花园的宽为x cm,围成的花园面积为y cm2,则y关于x的函数关系式为 .
y=x2-14x+48(0
3
14
(2)求玩具每天的销售利润w(单位:元)与售价x(单位:元)之间的函数关系式;
解:w=(x-10)(-10x+300)
=-10x2+400x-3 000.
(3)该商场为了让利给顾客,且每天获得750元利润,售价应定为多少?
解:要使w=750,即-10x2+400x-3 000=750,
解得x1=15,x2=25,
∵要让利给顾客,∴x=15.
答:为了让利给顾客,且每天获利750元,售价应定为15元/个.
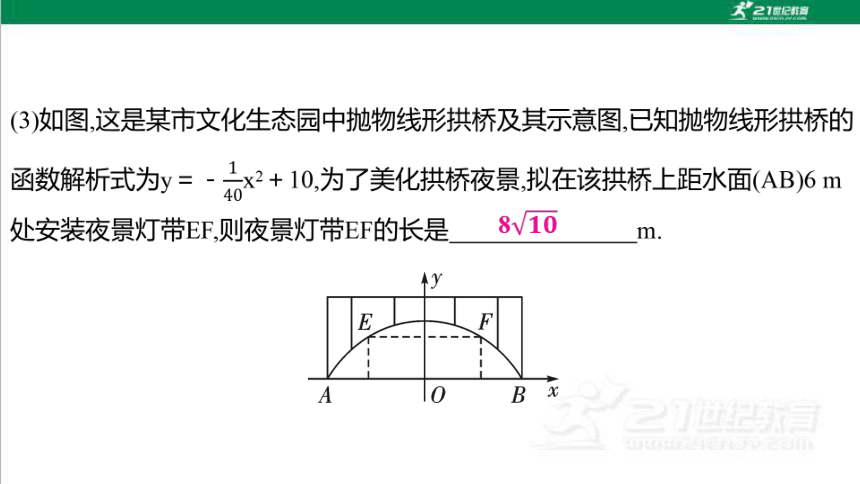
【方法归纳】此类问题一般涉及抛球、投篮、隧道、拱桥、喷泉水柱等,解决此类问题的关键是理解题目中的条件所表示的几何意义.最高点为抛物线的顶点,抛出点为抛物线中的c值,落地点为抛物线与x轴的交点,落地点到抛出点的水平距离是此落地点横坐标的绝对值.
(1)抛球运动判断球是否过网即判断此点的坐标是否在抛物线上方;
(2)投篮判断是否能投中即判断篮网是否在球的运动轨迹所在的抛物线上;
(3)判断车是否能通过隧道即判断车顶两端点的坐标是否在抛物线的下方;
(4)判断船是否能通过拱桥即判断船两端的高度是否比桥上对应点到水面的距离小;
(5)判断人是否会被喷泉淋湿即判断人所处位置的水的高度是否比人的身高要高.
【分层分析】(1)将点A坐标代入解析式可求a,即可求解;
(2)先画出能接到沙包的示意图,再根据点A的取值范围代入解析式可求解.
类型3:利用二次函数解决围栏面积问题
如图,某农户计划用篱笆围成一个矩形场地养殖家禽,为充分利用现有资源,该矩形场地一面靠墙(墙的长度为18 m),另外三面用篱笆围成,中间再用篱笆把它分成三个面积相等的矩形分别养殖不同的家禽,计划购买篱笆的总长度为 32 m,设矩形场地的长为x m, 宽为y m, 面积为S m2.
(1)分别求出y与x,S与x的函数解析式;
(2)当x为何值时,矩形场地的总面积最大?
最大面积为多少?
(1)求点A的坐标;
(2)求该抛物线的函数解析式;
(3)求起跳点A与着陆坡顶端C之间的水平距离OC的长.
(结果精确到0.1 m,参考数据:≈1.73)
解:(1)∵OA=4,且点A在y轴正半轴,∴A(0,4).
2.(2024·贵州)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(单位:盒)与销售单价x(单位:元)是一次函数关系,下表是y与x的几组对应值.
(1)求y与x的函数解析式;
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 … 56 52 48 44 40 …
解:(1)y与x的函数解析式为y=-2x+80.
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少?
解:(2)设日销售利润为w元,根据题意,得
w=(x-10)·y=(x-10)(-2x+80)
=-2(x-25)2+450,
∴当x=25时,w有最大值为450,
∴糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元.
3)若超市决定每销售一盒糖果便向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
同课章节目录
