中考数学复习第四章三角形第三节等腰三角形课件
文档属性
| 名称 | 中考数学复习第四章三角形第三节等腰三角形课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:22:00 | ||
图片预览







文档简介
(共22张PPT)
等腰三角形
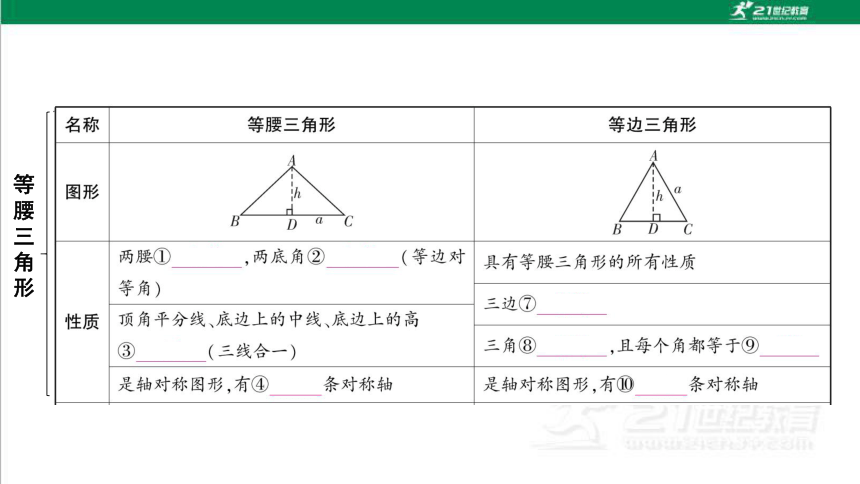
等腰三角形
【知识归纳1】
1.等腰三角形两腰上的高、中线和两底角的平分线都相等
如图,若AB=AC,CM⊥AB,BN⊥AC,E,F分别为AB,AC中点,BP,CQ分别为∠ABC,∠ACB的平分线,则CM=BN,CE=BF,BP=CQ.
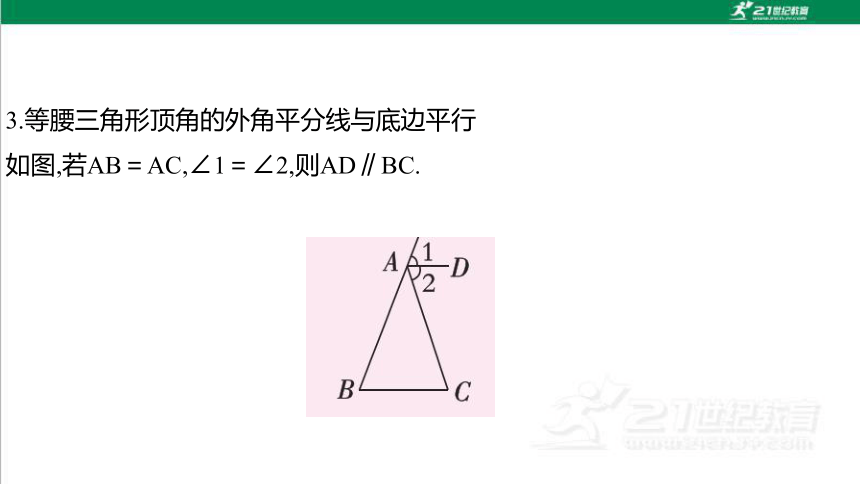
3.等腰三角形顶角的外角平分线与底边平行
如图,若AB=AC,∠1=∠2,则AD∥BC.
4.等腰三角形底边上任意一点到两腰的距离之和等于腰上的高
如图,若AB=AC,DE⊥AB,DF⊥AC,CH⊥AB,则DE+DF=CH.
【知识归纳2】构成等腰三角形的常见图形
1.垂直平分线
如图①,l为线段AB的垂直平分线,则△ABP为等腰三角形.
2.角平分线+平行线
(1)如图②,OC平分∠AOB ,CD∥OB,则△ODC为等腰三角形;
(2)如图③,AD平分∠BAC,CE∥AD,则△ACE为等腰三角形;
(3)如图④,在△ABC中,EF∥BC,BD平分∠ABC,CD平分∠ACB,则△BED和△CFD均为等腰三角形,且C△AEF=AE+AF+EF=AB+AC;
(4)如图⑤,在△ABC中,DE∥AB,DF∥AC,BD平分∠ABC,CD平分∠ACB,则△BED和△CFD均为等腰三角形,且C△DEF=DE+DF+EF=BC.
1.已知△ABC是等腰三角形,
(1)若∠A=80°,则等腰△ABC的顶角的度数为 ;
(2)若AB=BC=AC,则∠A= ;
(3)若AB=4,BC=8,则等腰△ABC的周长为 ;
(4)若等腰△ABC的周长为20,AB=4,则BC的长为 .
20°或80°
60°
20
8
2.如图,在△ABC中,D是BC上一点,连接AD.
(1)若AB=AD=DC,∠B=48°,则∠DAC= ;
(2)若△ABD是等边三角形,CD=AD,则∠C= ;
(3)若AB=4,BC=7,CD=3,∠B=60°,则AD= ;
(4)若AD垂直平分BC,∠B=60°,BD=1,则AB= ;
(5)若∠B=80°,∠BAD=20°,∠C=40°,AB=3,则图中有 个等腰三角形,CD= .
24°
30°
4
2
2
3
8
36°
3
20
重难点1:等腰三角形的性质应用
如图,△ABC为等腰三角形,AB=BC,点F是线段CB上一点,连接AF.
(1)如图①,若AF⊥CB,AB=10,BF=8,求线段AC的长;
(2)如图②,点E为线段AB上一点,连接CE,使∠ACE=∠B,且EA=BF,D为AF的中点,连接CD.延长BC至点G,使CG=CF,连接AG.求证:
∠ACD=∠BCE.
(2)证明:∵∠ACE=∠B,
∴∠ACE+∠BCE=∠B+∠BCE,∴∠ACB=∠AEC.
∵AB=BC,∴∠ACB=∠BAC,
∴∠AEC=∠BAC,∴AC=EC.
∵CG=CF,且D为AF的中点,
∴CD∥AG,∴∠ACD=∠GAC.
∵∠CEA=∠ACB,∴∠ACG=∠CEB.
∵AB=BC,AE=BF,∴BE=CF=CG.
又∵AC=CE,∴△ACG≌△CEB(SAS),
∴∠GAC=∠BCE,∴∠ACD=∠BCE.
重难点2:等边三角形的性质应用
如图,△ABC为等边三角形,点D,E分别在BA,AB的延长线上,且AD=BE,连接CD,CE.
(1)求证:CD=CE;
(2)若EF平分∠DEC分别交CD,CA于点F,G,
∠ACD=∠CEF,在EF上取点H,使EH=AC,
连接CH.求证:EF=AC+AD.
证明:(1)∵△ABC为等边三角形,
∴AC=BC,∠BAC=∠ABC=60,∴∠DAC=∠EBC.
在△DAC和△EBC中,
∴△DAC≌△EBC(SAS),∴CD=CE.
(2)在△CDA和△ECH中,
∴△CDA≌△ECH(SAS),∴AD=CH,∠D=∠HCE.
∵∠BAC=∠D+∠1=60°,∠1=∠2,∴∠CHF=∠HCE+∠2=60°,
∵EF平分∠DEC,∴∠2=∠3,∴∠1=∠3.
∵∠AGE=∠CGF,∴∠CFH=∠BAC=60°,
∴△CFH为等边三角形,
∴FH=CH,∴FH=AD,
∴EF=EH+FH=AC+AD.
等腰三角形
等腰三角形
【知识归纳1】
1.等腰三角形两腰上的高、中线和两底角的平分线都相等
如图,若AB=AC,CM⊥AB,BN⊥AC,E,F分别为AB,AC中点,BP,CQ分别为∠ABC,∠ACB的平分线,则CM=BN,CE=BF,BP=CQ.
3.等腰三角形顶角的外角平分线与底边平行
如图,若AB=AC,∠1=∠2,则AD∥BC.
4.等腰三角形底边上任意一点到两腰的距离之和等于腰上的高
如图,若AB=AC,DE⊥AB,DF⊥AC,CH⊥AB,则DE+DF=CH.
【知识归纳2】构成等腰三角形的常见图形
1.垂直平分线
如图①,l为线段AB的垂直平分线,则△ABP为等腰三角形.
2.角平分线+平行线
(1)如图②,OC平分∠AOB ,CD∥OB,则△ODC为等腰三角形;
(2)如图③,AD平分∠BAC,CE∥AD,则△ACE为等腰三角形;
(3)如图④,在△ABC中,EF∥BC,BD平分∠ABC,CD平分∠ACB,则△BED和△CFD均为等腰三角形,且C△AEF=AE+AF+EF=AB+AC;
(4)如图⑤,在△ABC中,DE∥AB,DF∥AC,BD平分∠ABC,CD平分∠ACB,则△BED和△CFD均为等腰三角形,且C△DEF=DE+DF+EF=BC.
1.已知△ABC是等腰三角形,
(1)若∠A=80°,则等腰△ABC的顶角的度数为 ;
(2)若AB=BC=AC,则∠A= ;
(3)若AB=4,BC=8,则等腰△ABC的周长为 ;
(4)若等腰△ABC的周长为20,AB=4,则BC的长为 .
20°或80°
60°
20
8
2.如图,在△ABC中,D是BC上一点,连接AD.
(1)若AB=AD=DC,∠B=48°,则∠DAC= ;
(2)若△ABD是等边三角形,CD=AD,则∠C= ;
(3)若AB=4,BC=7,CD=3,∠B=60°,则AD= ;
(4)若AD垂直平分BC,∠B=60°,BD=1,则AB= ;
(5)若∠B=80°,∠BAD=20°,∠C=40°,AB=3,则图中有 个等腰三角形,CD= .
24°
30°
4
2
2
3
8
36°
3
20
重难点1:等腰三角形的性质应用
如图,△ABC为等腰三角形,AB=BC,点F是线段CB上一点,连接AF.
(1)如图①,若AF⊥CB,AB=10,BF=8,求线段AC的长;
(2)如图②,点E为线段AB上一点,连接CE,使∠ACE=∠B,且EA=BF,D为AF的中点,连接CD.延长BC至点G,使CG=CF,连接AG.求证:
∠ACD=∠BCE.
(2)证明:∵∠ACE=∠B,
∴∠ACE+∠BCE=∠B+∠BCE,∴∠ACB=∠AEC.
∵AB=BC,∴∠ACB=∠BAC,
∴∠AEC=∠BAC,∴AC=EC.
∵CG=CF,且D为AF的中点,
∴CD∥AG,∴∠ACD=∠GAC.
∵∠CEA=∠ACB,∴∠ACG=∠CEB.
∵AB=BC,AE=BF,∴BE=CF=CG.
又∵AC=CE,∴△ACG≌△CEB(SAS),
∴∠GAC=∠BCE,∴∠ACD=∠BCE.
重难点2:等边三角形的性质应用
如图,△ABC为等边三角形,点D,E分别在BA,AB的延长线上,且AD=BE,连接CD,CE.
(1)求证:CD=CE;
(2)若EF平分∠DEC分别交CD,CA于点F,G,
∠ACD=∠CEF,在EF上取点H,使EH=AC,
连接CH.求证:EF=AC+AD.
证明:(1)∵△ABC为等边三角形,
∴AC=BC,∠BAC=∠ABC=60,∴∠DAC=∠EBC.
在△DAC和△EBC中,
∴△DAC≌△EBC(SAS),∴CD=CE.
(2)在△CDA和△ECH中,
∴△CDA≌△ECH(SAS),∴AD=CH,∠D=∠HCE.
∵∠BAC=∠D+∠1=60°,∠1=∠2,∴∠CHF=∠HCE+∠2=60°,
∵EF平分∠DEC,∴∠2=∠3,∴∠1=∠3.
∵∠AGE=∠CGF,∴∠CFH=∠BAC=60°,
∴△CFH为等边三角形,
∴FH=CH,∴FH=AD,
∴EF=EH+FH=AC+AD.
同课章节目录
