中考数学复习第四章三角形微专题(五)全等与相似的常见模型课件
文档属性
| 名称 | 中考数学复习第四章三角形微专题(五)全等与相似的常见模型课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:22:00 | ||
图片预览






文档简介
(共19张PPT)
模型1 “A”字模型
模型 正“A”字型 斜“A”字型
(共角) 斜“A”字型
(共边)
图示
DE∥BC
∠1=∠C
(∠2=∠B)
∠1=∠B
(∠2=∠ACB)
结论 △ADE∽△ABC △ADE∽△ACB △ACD∽△ABC,
AC2=AD·AB
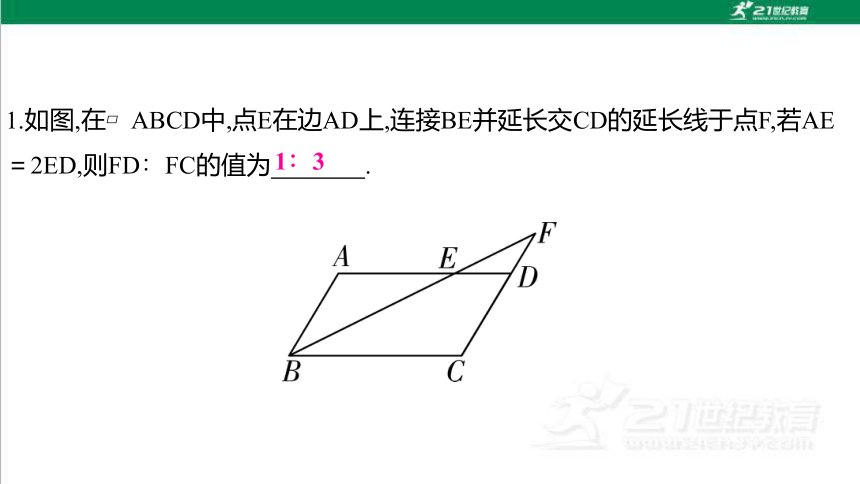
1.如图,在 ABCD中,点E在边AD上,连接BE并延长交CD的延长线于点F,若AE=2ED,则FD∶FC的值为 .
1∶3
2.如图,在Rt△ABC中,∠C=90°,D是AB边上的点,DE⊥AB交AC于点E,AD=4,AE=5,AB=10,则BC的长为 .
6
模型2 “8”字模型
模型 正“8”字型 斜“8”字
(蝴蝶型) 斜“8”字
(燕尾型)
图示
AB∥CD
(∠A=∠C)
∠A=∠C
∠A=∠C
结论 △AOB∽△COD △AOB∽△COD
OA·OD=OB·OC △ABF∽△CDF
△AED∽△CEB
3.如图,正方形ABCD的边长为5,正方形EFGC的边长为3,点B,C,G在一条直线上.连接BF,则图中阴影部分的面积为 .
模型3 一线三等角模型
模型 同侧一线三等角 异侧一线三等角
图示
锐角一线三等角
锐角一线三等角
一线三垂直
一线三垂直
钝角一线三等角
钝角一线三等角
条件 两个三角形在直线同侧,点P在线段AB上,∠1=∠2=∠3 两个三角形在直线异侧,点P在AB的延长线上,∠1=∠2=∠3
结论 △CAP∽△PBD △CAP∽△PBD
B
【解析】易得△BDE∽△CAD.
6.(模型构造)如图,在矩形ABCD中,AB=4,BC=8,E是BC上一点,且BE=3,连接AE,将线段AE绕点E顺时针旋转90°得到线段EF,连接CF,则△ECF的面积为 .
【解析】过点F作FG⊥BC于点G,则△ABE≌△EGF,∴BE=FG=3.
模型4 “手拉手”全等模型
图示
OC在△OAB内且拉手线无交点 OC在△OAB外且拉手线无交点 OC在△OAB外且拉手线有交点
条件 在等腰三角形OAB中,OA=OB;在等腰三角形OCD中,OC=OD,∠AOB=∠COD=α,将△OCD绕点O旋转一定角度后,连接AC,BD(称为“拉手线”,左手拉左手,右手拉右手),相交于点E,连接OE
结论 1.△AOC≌△BOD,AC=BD(即拉手线相等);
2.EO平分∠AED;
3.∠AEB=∠AOB=α
旋转
构造
“手拉
手”模
型的
步骤 1.先找有没有“等线段,共顶点”;
2.选择其中一个三角形,将其经过“共顶点”的线段旋转;
3.旋转方向与这个三角形的“等线段”旋转到另一条“等线段”的方向一致,旋转角为“等线段”间的夹角
7.如图,在△ABC和△ADE中,AB=AC,AD=AE,点B,D,E在同一条直线上,∠BAC=∠DAE.若∠BAD=28°,∠AED=62°,则∠ACE的度数为 .
34°
模型5 “手拉手”相似模型
图示
AD在△ABC内且拉手线无交点
AD在△ABC外且拉手线无交点
AD在△ABC外且拉手线有交点
条件 在△ABC中,点D,E分别在边AB,AC上,DE∥BC,将△ADE绕点A旋转
结论 1.△ADE∽△ABC,△ADB∽△AEC;
2.两条拉手线BD,CE交于点F,则
(1)∠BFC=∠BAC=α;
(2)点A,B,C,F四点共圆
8.如图,在△ABC和△ADE中,∠ACB=∠AED,∠EAC=∠DAB,连接BD,CE,若∠ACE=25°,则∠ABD= .
25°
简写过程:
模型1 “A”字模型
模型 正“A”字型 斜“A”字型
(共角) 斜“A”字型
(共边)
图示
DE∥BC
∠1=∠C
(∠2=∠B)
∠1=∠B
(∠2=∠ACB)
结论 △ADE∽△ABC △ADE∽△ACB △ACD∽△ABC,
AC2=AD·AB
1.如图,在 ABCD中,点E在边AD上,连接BE并延长交CD的延长线于点F,若AE=2ED,则FD∶FC的值为 .
1∶3
2.如图,在Rt△ABC中,∠C=90°,D是AB边上的点,DE⊥AB交AC于点E,AD=4,AE=5,AB=10,则BC的长为 .
6
模型2 “8”字模型
模型 正“8”字型 斜“8”字
(蝴蝶型) 斜“8”字
(燕尾型)
图示
AB∥CD
(∠A=∠C)
∠A=∠C
∠A=∠C
结论 △AOB∽△COD △AOB∽△COD
OA·OD=OB·OC △ABF∽△CDF
△AED∽△CEB
3.如图,正方形ABCD的边长为5,正方形EFGC的边长为3,点B,C,G在一条直线上.连接BF,则图中阴影部分的面积为 .
模型3 一线三等角模型
模型 同侧一线三等角 异侧一线三等角
图示
锐角一线三等角
锐角一线三等角
一线三垂直
一线三垂直
钝角一线三等角
钝角一线三等角
条件 两个三角形在直线同侧,点P在线段AB上,∠1=∠2=∠3 两个三角形在直线异侧,点P在AB的延长线上,∠1=∠2=∠3
结论 △CAP∽△PBD △CAP∽△PBD
B
【解析】易得△BDE∽△CAD.
6.(模型构造)如图,在矩形ABCD中,AB=4,BC=8,E是BC上一点,且BE=3,连接AE,将线段AE绕点E顺时针旋转90°得到线段EF,连接CF,则△ECF的面积为 .
【解析】过点F作FG⊥BC于点G,则△ABE≌△EGF,∴BE=FG=3.
模型4 “手拉手”全等模型
图示
OC在△OAB内且拉手线无交点 OC在△OAB外且拉手线无交点 OC在△OAB外且拉手线有交点
条件 在等腰三角形OAB中,OA=OB;在等腰三角形OCD中,OC=OD,∠AOB=∠COD=α,将△OCD绕点O旋转一定角度后,连接AC,BD(称为“拉手线”,左手拉左手,右手拉右手),相交于点E,连接OE
结论 1.△AOC≌△BOD,AC=BD(即拉手线相等);
2.EO平分∠AED;
3.∠AEB=∠AOB=α
旋转
构造
“手拉
手”模
型的
步骤 1.先找有没有“等线段,共顶点”;
2.选择其中一个三角形,将其经过“共顶点”的线段旋转;
3.旋转方向与这个三角形的“等线段”旋转到另一条“等线段”的方向一致,旋转角为“等线段”间的夹角
7.如图,在△ABC和△ADE中,AB=AC,AD=AE,点B,D,E在同一条直线上,∠BAC=∠DAE.若∠BAD=28°,∠AED=62°,则∠ACE的度数为 .
34°
模型5 “手拉手”相似模型
图示
AD在△ABC内且拉手线无交点
AD在△ABC外且拉手线无交点
AD在△ABC外且拉手线有交点
条件 在△ABC中,点D,E分别在边AB,AC上,DE∥BC,将△ADE绕点A旋转
结论 1.△ADE∽△ABC,△ADB∽△AEC;
2.两条拉手线BD,CE交于点F,则
(1)∠BFC=∠BAC=α;
(2)点A,B,C,F四点共圆
8.如图,在△ABC和△ADE中,∠ACB=∠AED,∠EAC=∠DAB,连接BD,CE,若∠ACE=25°,则∠ABD= .
25°
简写过程:
同课章节目录
