中考数学复习第四章三角形第五节全等三角形课件
文档属性
| 名称 | 中考数学复习第四章三角形第五节全等三角形课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 886.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:22:00 | ||
图片预览




文档简介
(共16张PPT)
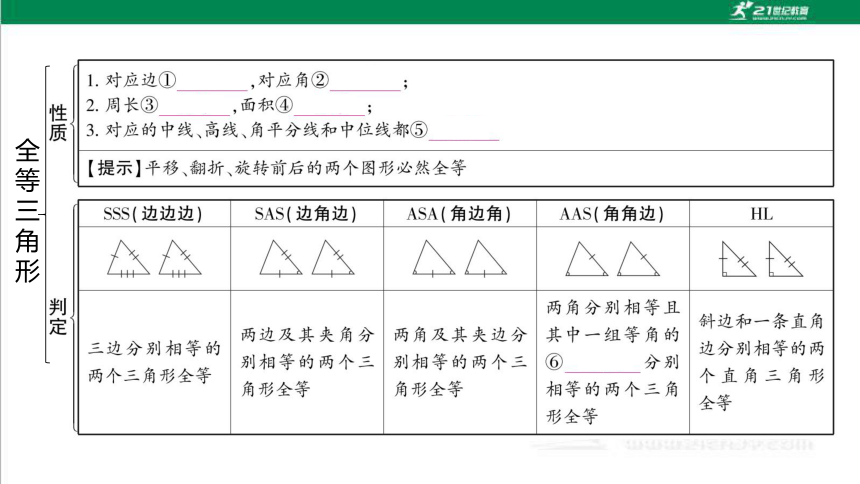
全等三角形
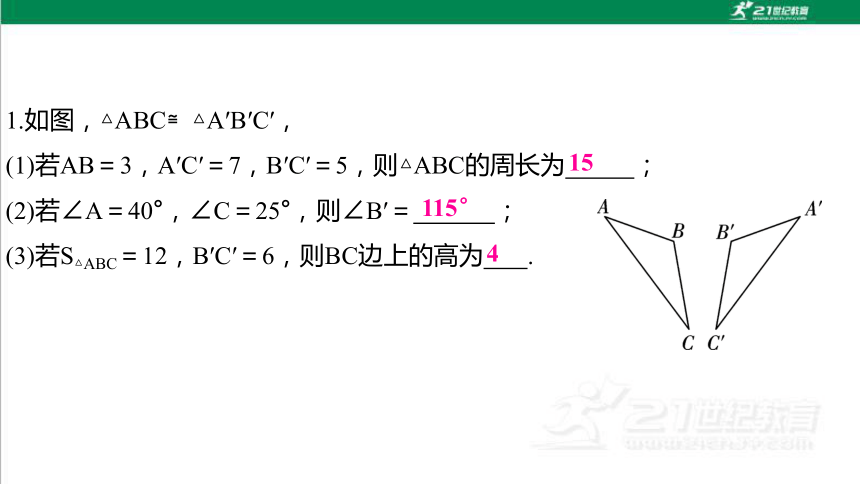
1.如图,△ABC≌△A′B′C′,
(1)若AB=3,A′C′=7,B′C′=5,则△ABC的周长为 ;
(2)若∠A=40°,∠C=25°,则∠B′= ;
(3)若S△ABC=12,B′C′=6,则BC边上的高为 .
15
115°
4
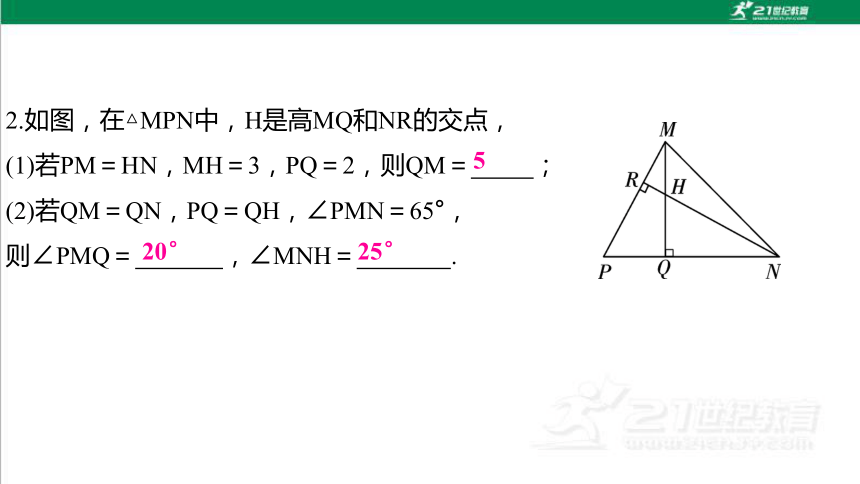
2.如图,在△MPN中,H是高MQ和NR的交点,
(1)若PM=HN,MH=3,PQ=2,则QM= ;
(2)若QM=QN,PQ=QH,∠PMN=65°,
则∠PMQ= ,∠MNH= .
5
20°
25°
3.(人教八上P44习题11题改编)如图,点A,B,C,D在同一直线上,在横线上添加适当的条件使得△AEC≌△DFB(不添加任何辅助线),并说明判定方法.
(1)已知AE=DF,EC=FB.
①添加的条件为 ,判定方法为SSS;
②添加的条件为 ,判定方法为SAS;
③添加的条件为 ,判定方法为HL;
AB=CD(或AC=DB)
∠E=∠F
∠A=∠D=90°(或∠ECA=∠FBD=90°)
(2)已知EA∥DF,EC∥BF.
①添加的条件为 ,判定方法为ASA;
②添加的条件为 ,判定方法为AAS;
(3)已知EC∥BF,AE=DF,添加的条件为 ,判定方法为 .
AC=BD(或AB=DC)
AE=DF(或CE=BF)
∠E=∠F(或∠A=∠D或AE∥DF)
AAS
重难点:全等三角形的性质与判定
如图,在△ABC中,BD是边AC的高,BE是∠CBD的平分线,且AD=DE,AO为△ABC的中线,延长AO到点F,使得BF∥AC,连接EF交BC于点G.
(1)求证:BF=CD+DE;
(2)若∠C=45°,求证:BD=BG.
证明:(1)∵BF∥AC,∴∠BFO=∠CAO,∠FBO=∠ACO,
又∵AO为△ABC的中线,∴BO=CO,
∴△BOF≌△COA(AAS),∴BF=CA=CD+AD,
∵AD=DE,∴BF=CD+DE.
2)∵BD垂直平分AE,∴BA=BE,∠BAC=∠BEA,
∵BE平分∠CBD,∴∠GBE=∠DBE.
又∵BF∥AC,∴∠BEA=∠EBF=∠BAC,
∴△BAC≌△EBF(SAS),∴∠BFE=∠C=45°,
∵BE平分∠CBD,∴∠GBE=∠DBE,
又∵∠BGE=∠C+∠FEC=90°=∠BDE,
∴△BEG≌△BED(AAS),∴BG=BD.
(2023·临沂)如图,∠BAC=90°,AB=AC,BD⊥AB,BC=AB+BD.
(1)写出AB与BD的数量关系;
(2)延长BC到点E,使CE=BC,延长DC到点F,使CF=DC,连接EF.求证:EF⊥AB.
(2)证明:在△BCD和△ECF中,
∴△BCD≌△ECF(SAS),
∴∠CBD=∠E=45°,BD=EF,∴BD∥EF,
∵BD⊥AB,∴EF⊥AB.
(1)解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠MAF=∠ACB,∵∠ACB=∠GAF,
∴∠GAF=∠MAF,∵BC=AD=2AG,AM=DM,
∴AG=AM,∵AF=AF,∴△AFG≌△AFM(SAS),
∴∠AFG=∠AFM=∠CFD=75°,
∴∠MFD=180°-75°-75°=30°.
命题点:全等三角形的判定与性质(每年考1~2次,2022年单独考查,其他均在几何证明与计算中涉及)
(2022·宁夏第10题3分)如图,AC,BD相交于点O,OB=OD,要使
△AOB≌△COD,添加一个条件是 .(只写一个)
OA=OC(答案不唯一)
全等三角形
1.如图,△ABC≌△A′B′C′,
(1)若AB=3,A′C′=7,B′C′=5,则△ABC的周长为 ;
(2)若∠A=40°,∠C=25°,则∠B′= ;
(3)若S△ABC=12,B′C′=6,则BC边上的高为 .
15
115°
4
2.如图,在△MPN中,H是高MQ和NR的交点,
(1)若PM=HN,MH=3,PQ=2,则QM= ;
(2)若QM=QN,PQ=QH,∠PMN=65°,
则∠PMQ= ,∠MNH= .
5
20°
25°
3.(人教八上P44习题11题改编)如图,点A,B,C,D在同一直线上,在横线上添加适当的条件使得△AEC≌△DFB(不添加任何辅助线),并说明判定方法.
(1)已知AE=DF,EC=FB.
①添加的条件为 ,判定方法为SSS;
②添加的条件为 ,判定方法为SAS;
③添加的条件为 ,判定方法为HL;
AB=CD(或AC=DB)
∠E=∠F
∠A=∠D=90°(或∠ECA=∠FBD=90°)
(2)已知EA∥DF,EC∥BF.
①添加的条件为 ,判定方法为ASA;
②添加的条件为 ,判定方法为AAS;
(3)已知EC∥BF,AE=DF,添加的条件为 ,判定方法为 .
AC=BD(或AB=DC)
AE=DF(或CE=BF)
∠E=∠F(或∠A=∠D或AE∥DF)
AAS
重难点:全等三角形的性质与判定
如图,在△ABC中,BD是边AC的高,BE是∠CBD的平分线,且AD=DE,AO为△ABC的中线,延长AO到点F,使得BF∥AC,连接EF交BC于点G.
(1)求证:BF=CD+DE;
(2)若∠C=45°,求证:BD=BG.
证明:(1)∵BF∥AC,∴∠BFO=∠CAO,∠FBO=∠ACO,
又∵AO为△ABC的中线,∴BO=CO,
∴△BOF≌△COA(AAS),∴BF=CA=CD+AD,
∵AD=DE,∴BF=CD+DE.
2)∵BD垂直平分AE,∴BA=BE,∠BAC=∠BEA,
∵BE平分∠CBD,∴∠GBE=∠DBE.
又∵BF∥AC,∴∠BEA=∠EBF=∠BAC,
∴△BAC≌△EBF(SAS),∴∠BFE=∠C=45°,
∵BE平分∠CBD,∴∠GBE=∠DBE,
又∵∠BGE=∠C+∠FEC=90°=∠BDE,
∴△BEG≌△BED(AAS),∴BG=BD.
(2023·临沂)如图,∠BAC=90°,AB=AC,BD⊥AB,BC=AB+BD.
(1)写出AB与BD的数量关系;
(2)延长BC到点E,使CE=BC,延长DC到点F,使CF=DC,连接EF.求证:EF⊥AB.
(2)证明:在△BCD和△ECF中,
∴△BCD≌△ECF(SAS),
∴∠CBD=∠E=45°,BD=EF,∴BD∥EF,
∵BD⊥AB,∴EF⊥AB.
(1)解:∵四边形ABCD是平行四边形,
∴AD=BC,AD∥BC,
∴∠MAF=∠ACB,∵∠ACB=∠GAF,
∴∠GAF=∠MAF,∵BC=AD=2AG,AM=DM,
∴AG=AM,∵AF=AF,∴△AFG≌△AFM(SAS),
∴∠AFG=∠AFM=∠CFD=75°,
∴∠MFD=180°-75°-75°=30°.
命题点:全等三角形的判定与性质(每年考1~2次,2022年单独考查,其他均在几何证明与计算中涉及)
(2022·宁夏第10题3分)如图,AC,BD相交于点O,OB=OD,要使
△AOB≌△COD,添加一个条件是 .(只写一个)
OA=OC(答案不唯一)
同课章节目录
