中考数学复习第四章三角形第七节锐角三角函数与解直角三角形的实际应用课件
文档属性
| 名称 | 中考数学复习第四章三角形第七节锐角三角函数与解直角三角形的实际应用课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:22:00 | ||
图片预览




文档简介
(共16张PPT)
锐角三角函数与解直角三角形的实际应用
锐角三角函数与解直角三角形的实际应用
锐角三角函数与解直角三角形的实际应用
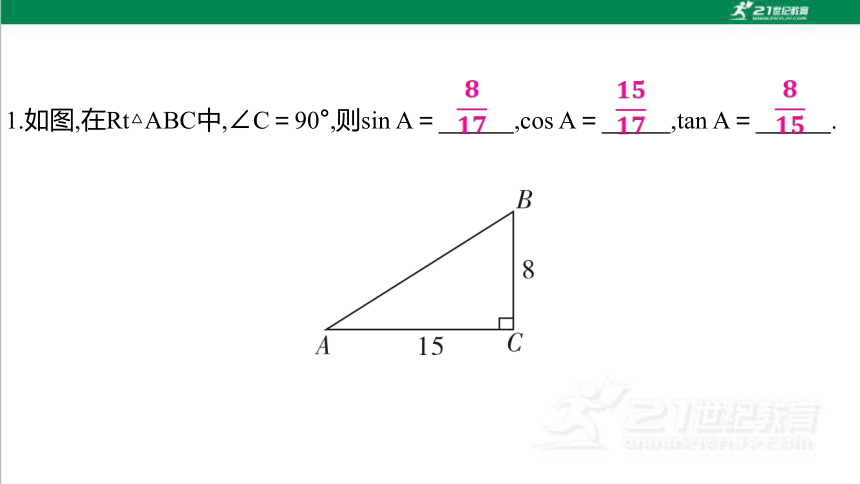
1.如图,在Rt△ABC中,∠C=90°,则sin A= ,cos A= ,tan A= .
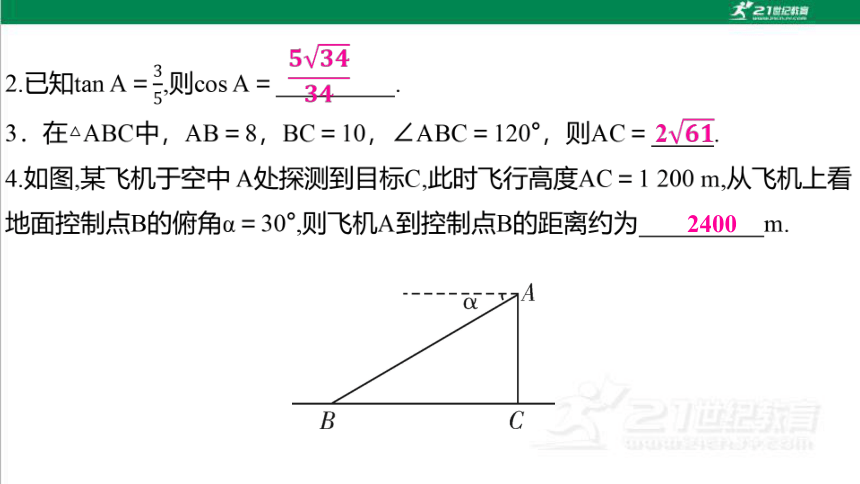
2400
5.如图,一艘船从A处向北偏东30°的方向行驶10 km到B处,再从B处向正西方向行驶30 km到C处,此时这艘船与A处的距离是 km.
6.如图,大坝横截面迎水坡AB的坡比为2∶1,若坝高AC为12 m,则迎水坡AB的长为 m.
命题点1:解直角三角形(近5年考查4次,仅 2023年单独考查)
B
命题点2:解直角三角形的实际应用(近5年考查4次)
34.1
3.(2023·宁夏第22题6分)如图,粮库用传送带传送粮袋,大转动轮的半径为10 cm,传送带与
水平面成30°角.假设传送带与转动轮之间无滑动,当大转动轮转140°时,传送带上点A处的粮袋上升的高度是多少?(传送带厚度忽略不计)
B
2门世2有
3厚
第七节锐角三角函数与解直角三
角形的实际应用
文字描述
图示
如图,在Rt△ABC中,∠C=90°,
【拓展】锐角三角函数之间的关系:
∠A为△ABC中的一个锐角,则有:
sin2 A cos2 A =1,
定
∠A的正弦:sinA=①
斜边c
cosA=sin(90°-A),
义
邻边b
sinA=cos(90°-A),
∠A的余弦:C0sA=②
6
B
对边a
tan A=.
sin A
cos A
∠A的正切:tanA=③
b
直角
三边关系
a2+b2=④c2
三角
形的
三角关系
∠A+∠B=∠C=⑤90°
边角
边角关系
sinA=cosB=⑥-
,co8A=sinB=⑦
b
,tanA=⑧
关系
b
tan B
念
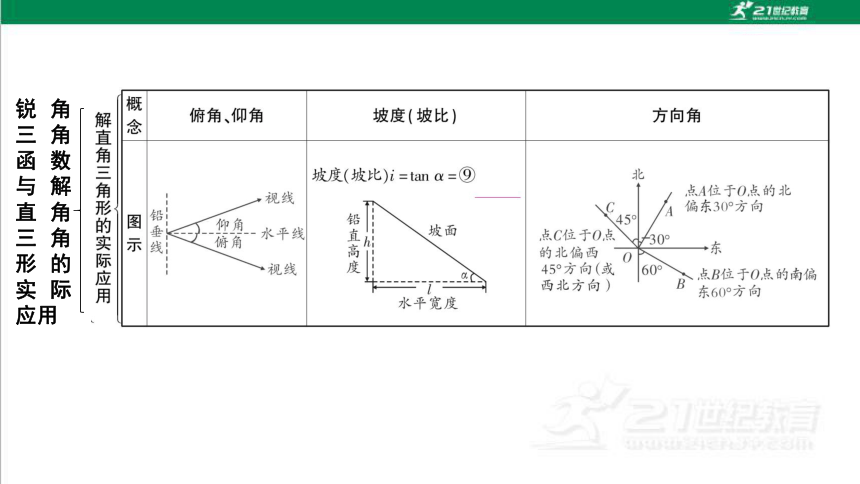
俯角、仰角
坡度(坡比)
方向角
解直角三角形的实际应用
坡度(坡比)i=tan=⑨
北
,视线
,点A位于O,点的北
图示
仰角
C59
偏东30°方向
坡面
俯角
水平线
直高度
点C位于O,点
230°
的北偏西
*东
视线
45°方向(或
60°
点B位于O,点的南偏
西北方向)
B
东60°方向
水平宽度
锐角三角函数与解直角三角形的实际应用
锐角三角函数与解直角三角形的实际应用
锐角三角函数与解直角三角形的实际应用
1.如图,在Rt△ABC中,∠C=90°,则sin A= ,cos A= ,tan A= .
2400
5.如图,一艘船从A处向北偏东30°的方向行驶10 km到B处,再从B处向正西方向行驶30 km到C处,此时这艘船与A处的距离是 km.
6.如图,大坝横截面迎水坡AB的坡比为2∶1,若坝高AC为12 m,则迎水坡AB的长为 m.
命题点1:解直角三角形(近5年考查4次,仅 2023年单独考查)
B
命题点2:解直角三角形的实际应用(近5年考查4次)
34.1
3.(2023·宁夏第22题6分)如图,粮库用传送带传送粮袋,大转动轮的半径为10 cm,传送带与
水平面成30°角.假设传送带与转动轮之间无滑动,当大转动轮转140°时,传送带上点A处的粮袋上升的高度是多少?(传送带厚度忽略不计)
B
2门世2有
3厚
第七节锐角三角函数与解直角三
角形的实际应用
文字描述
图示
如图,在Rt△ABC中,∠C=90°,
【拓展】锐角三角函数之间的关系:
∠A为△ABC中的一个锐角,则有:
sin2 A cos2 A =1,
定
∠A的正弦:sinA=①
斜边c
cosA=sin(90°-A),
义
邻边b
sinA=cos(90°-A),
∠A的余弦:C0sA=②
6
B
对边a
tan A=.
sin A
cos A
∠A的正切:tanA=③
b
直角
三边关系
a2+b2=④c2
三角
形的
三角关系
∠A+∠B=∠C=⑤90°
边角
边角关系
sinA=cosB=⑥-
,co8A=sinB=⑦
b
,tanA=⑧
关系
b
tan B
念
俯角、仰角
坡度(坡比)
方向角
解直角三角形的实际应用
坡度(坡比)i=tan=⑨
北
,视线
,点A位于O,点的北
图示
仰角
C59
偏东30°方向
坡面
俯角
水平线
直高度
点C位于O,点
230°
的北偏西
*东
视线
45°方向(或
60°
点B位于O,点的南偏
西北方向)
B
东60°方向
水平宽度
同课章节目录
