中考数学复习第四章三角形微专题(三)与中点有关的辅助线课件
文档属性
| 名称 | 中考数学复习第四章三角形微专题(三)与中点有关的辅助线课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 00:00:00 | ||
图片预览

文档简介
(共19张PPT)
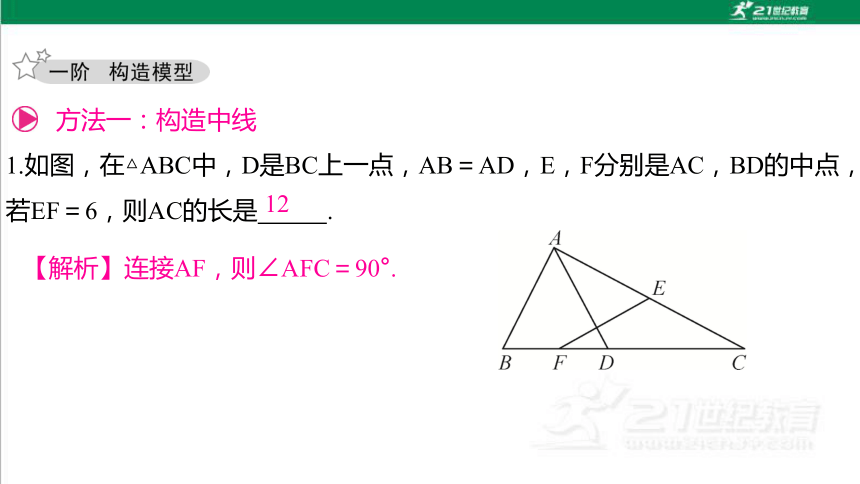
方法一:构造中线
1.如图,在△ABC中,D是BC上一点,AB=AD,E,F分别是AC,BD的中点,若EF=6,则AC的长是 .
12
【解析】连接AF,则∠AFC=90°.
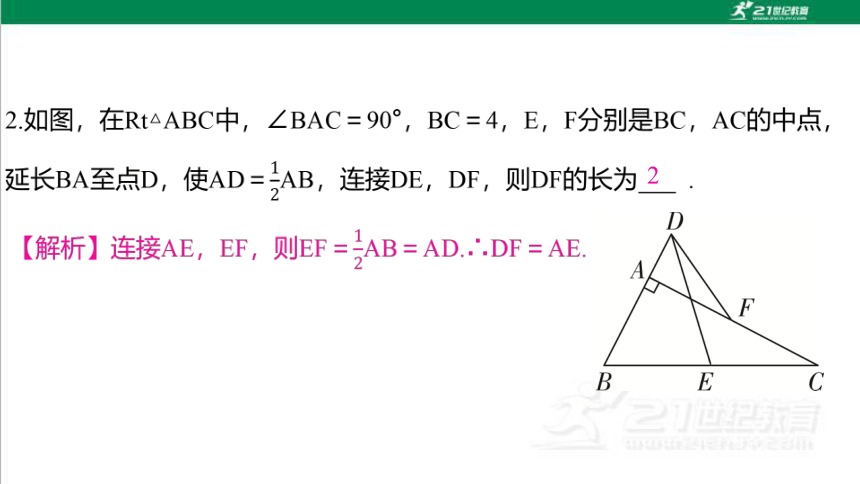
2
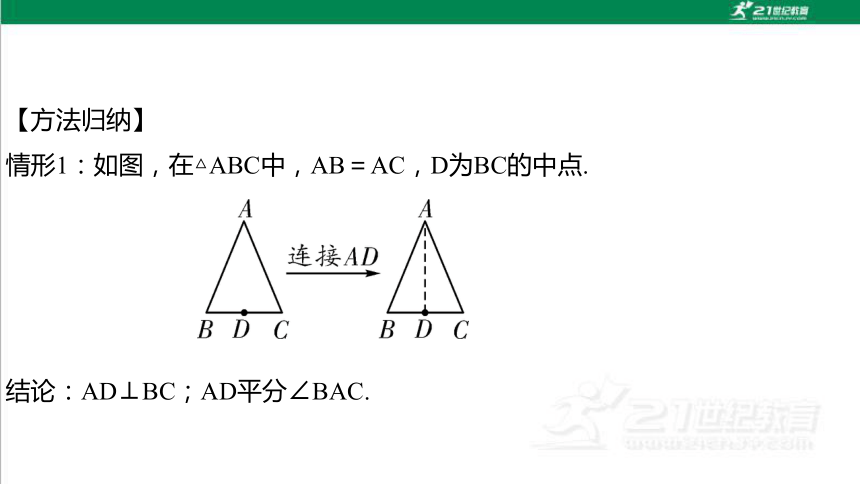
【方法归纳】
情形1:如图,在△ABC中,AB=AC,D为BC的中点.
结论:AD⊥BC;AD平分∠BAC.
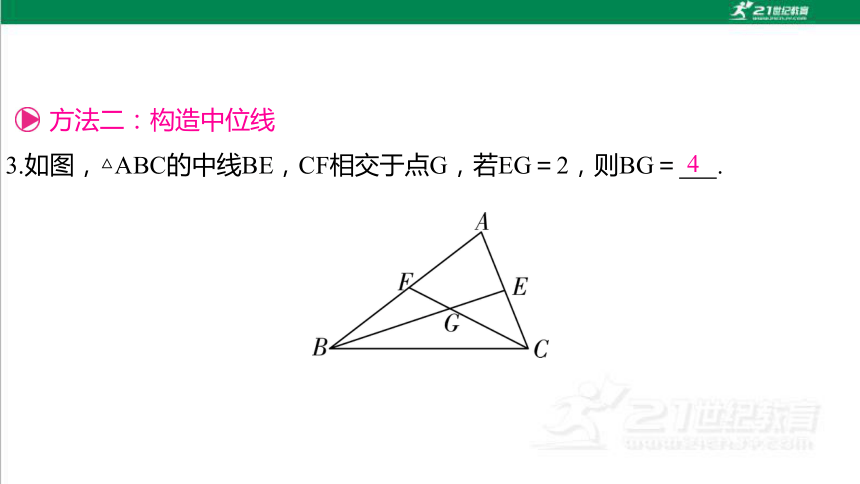
方法二:构造中位线
3.如图,△ABC的中线BE,CF相交于点G,若EG=2,则BG= .
4
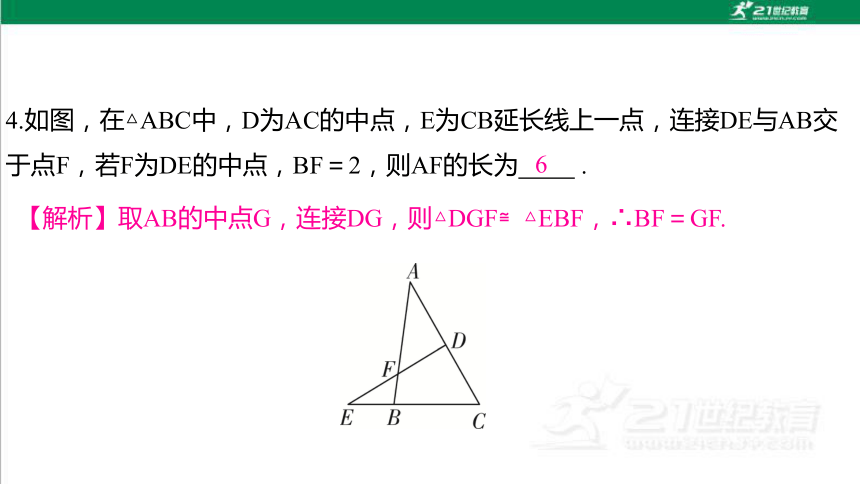
4.如图,在△ABC中,D为AC的中点,E为CB延长线上一点,连接DE与AB交于点F,若F为DE的中点,BF=2,则AF的长为 .
6
【解析】取AB的中点G,连接DG,则△DGF≌△EBF,∴BF=GF.
方法三:遇到中线,考虑构造倍长中线或倍长类中线
5.如图,AD是△ABC的中线,在AD上取一点F,连接BF并延长交AC于点E,若AE=EF,求证:AC=BF.
证明:延长AD至点H,使DH=AD,连接BH,
∵AD是△ABC的中线,∴BD=CD,
∴△ADC≌△HDB(SAS),
∴AC=HB,∠CAD=∠H,
∵AE=EF,∴∠EAF=∠AFE=∠BFH,
∴∠H=∠BFH,∴BF=BH,∴AC=BF.
【方法归纳】
情形1:倍长中线
如图,在△ABC中,AD是BC边的中线.
辅助线作法一:延长AD至点E,使DE=AD,连接BE.
6.如图,△ABC中,D是BC的中点,DE⊥DF,试判断BE+CF与EF的大小关系,并证明你的结论.
辅助线作法二:过点B作BE∥AC交AD的延长线于点E.
结论:△ACD≌△EBD.
情形2:倍长类中线
如图,在△ABC中,D是边BC的中点,E是边AB上一点,连接DE.
辅助线作法一:延长ED至点F,使DF=ED,连接CF.
辅助线作法二:过点C作CF∥AB交ED的延长线于点F.
结论:△BDE≌△CDF.
【解析】延长BC至点F,使CF=CA,连接AF,根据等边三角形的性质求出AF,根据三角形中位线定理得DE的长.
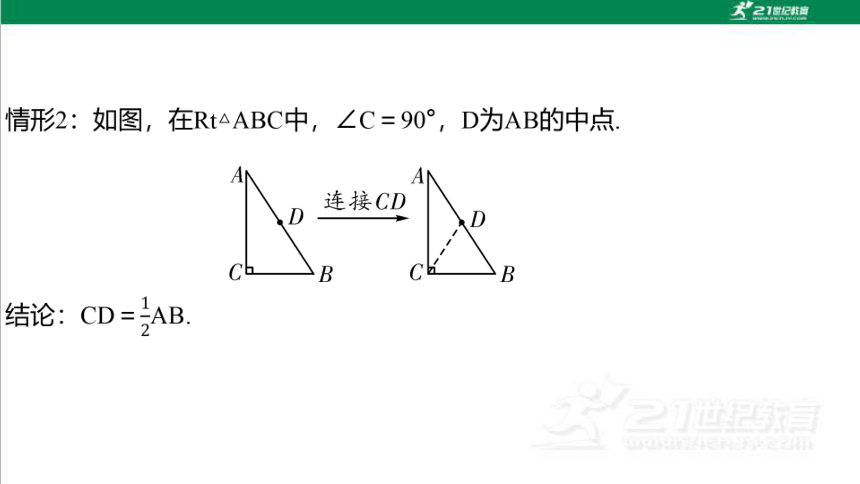
9.如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16 cm,则线段CD的长是 cm.
8
【解析】连接CM,根据直角三角形斜边上中线得到BM=CM,推出∠B=∠MCB,根据三角形外角性质求出∠D=∠DMC,推出DC=CM,即可求出答案.
10.如图,在△ABC中,D是BC上一点,连接AD,AE是BD边上的中线,且AB=BD=CD,求证:AD平分∠CAE.
证明:延长AE至点F,使 EF=EA,连接DF.
∵AE是BD边上的中线,∴BE=DE.∴△DEF≌△BEA(SAS).
∴FD=AB,∠EDF=∠B.
∵AB=BD,∴∠BAD=∠BDA.
又∵CD=AB,∠ADC=∠BAD+∠B,
∠ADF=∠BDA+∠EDF,
∴CD=FD,∠ADC=∠ADF.
又∵AD=AD,∴△ADC≌△ADF(SAS),
∴∠CAD=∠FAD,∴AD平分∠CAE.
方法一:构造中线
1.如图,在△ABC中,D是BC上一点,AB=AD,E,F分别是AC,BD的中点,若EF=6,则AC的长是 .
12
【解析】连接AF,则∠AFC=90°.
2
【方法归纳】
情形1:如图,在△ABC中,AB=AC,D为BC的中点.
结论:AD⊥BC;AD平分∠BAC.
方法二:构造中位线
3.如图,△ABC的中线BE,CF相交于点G,若EG=2,则BG= .
4
4.如图,在△ABC中,D为AC的中点,E为CB延长线上一点,连接DE与AB交于点F,若F为DE的中点,BF=2,则AF的长为 .
6
【解析】取AB的中点G,连接DG,则△DGF≌△EBF,∴BF=GF.
方法三:遇到中线,考虑构造倍长中线或倍长类中线
5.如图,AD是△ABC的中线,在AD上取一点F,连接BF并延长交AC于点E,若AE=EF,求证:AC=BF.
证明:延长AD至点H,使DH=AD,连接BH,
∵AD是△ABC的中线,∴BD=CD,
∴△ADC≌△HDB(SAS),
∴AC=HB,∠CAD=∠H,
∵AE=EF,∴∠EAF=∠AFE=∠BFH,
∴∠H=∠BFH,∴BF=BH,∴AC=BF.
【方法归纳】
情形1:倍长中线
如图,在△ABC中,AD是BC边的中线.
辅助线作法一:延长AD至点E,使DE=AD,连接BE.
6.如图,△ABC中,D是BC的中点,DE⊥DF,试判断BE+CF与EF的大小关系,并证明你的结论.
辅助线作法二:过点B作BE∥AC交AD的延长线于点E.
结论:△ACD≌△EBD.
情形2:倍长类中线
如图,在△ABC中,D是边BC的中点,E是边AB上一点,连接DE.
辅助线作法一:延长ED至点F,使DF=ED,连接CF.
辅助线作法二:过点C作CF∥AB交ED的延长线于点F.
结论:△BDE≌△CDF.
【解析】延长BC至点F,使CF=CA,连接AF,根据等边三角形的性质求出AF,根据三角形中位线定理得DE的长.
9.如图,M是Rt△ABC斜边AB上的中点,D是边BC延长线上一点,∠B=2∠D,AB=16 cm,则线段CD的长是 cm.
8
【解析】连接CM,根据直角三角形斜边上中线得到BM=CM,推出∠B=∠MCB,根据三角形外角性质求出∠D=∠DMC,推出DC=CM,即可求出答案.
10.如图,在△ABC中,D是BC上一点,连接AD,AE是BD边上的中线,且AB=BD=CD,求证:AD平分∠CAE.
证明:延长AE至点F,使 EF=EA,连接DF.
∵AE是BD边上的中线,∴BE=DE.∴△DEF≌△BEA(SAS).
∴FD=AB,∠EDF=∠B.
∵AB=BD,∴∠BAD=∠BDA.
又∵CD=AB,∠ADC=∠BAD+∠B,
∠ADF=∠BDA+∠EDF,
∴CD=FD,∠ADC=∠ADF.
又∵AD=AD,∴△ADC≌△ADF(SAS),
∴∠CAD=∠FAD,∴AD平分∠CAE.
同课章节目录
