中考数学复习第四章三角形微专题(四)与角平分线有关的辅助线课件
文档属性
| 名称 | 中考数学复习第四章三角形微专题(四)与角平分线有关的辅助线课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 935.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:22:00 | ||
图片预览




文档简介
(共19张PPT)
方法一:利用角平分线性质构造对称图形
1.如图,在△ABC中,AD平分∠BAC,DE∥AB交AC于点E,CE=6,DE=5,过点D作DF⊥AB于点F,若DF=4,则△ACD的面积为( )
A.20
B.22
C.24
D.26
B
【方法归纳】
1.过角平分线上的点向角两边作垂线
如图①,点P在∠MON的平分线上,PA⊥OM,过点P作PB⊥ON于点B.
结论:AP=BP,Rt△AOP≌Rt△BOP.
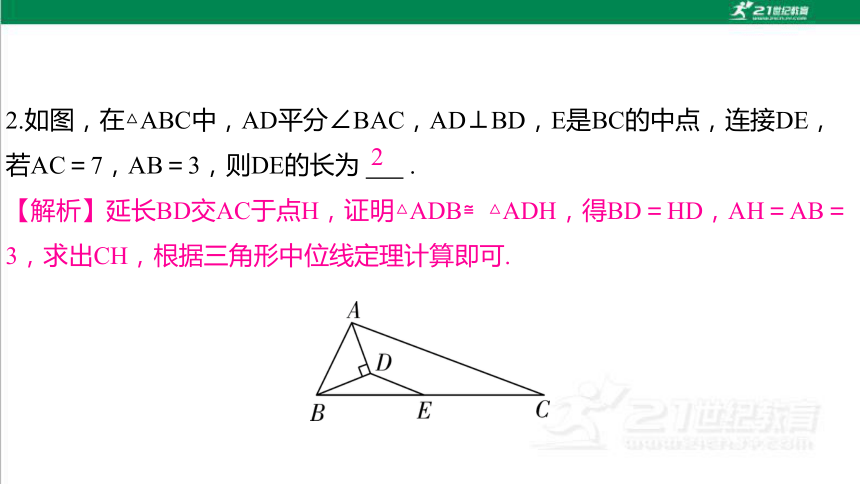
2.如图,在△ABC中,AD平分∠BAC,AD⊥BD,E是BC的中点,连接DE,若AC=7,AB=3,则DE的长为 .
【解析】延长BD交AC于点H,证明△ADB≌△ADH,得BD=HD,AH=AB=3,求出CH,根据三角形中位线定理计算即可.
2
2.过角平分线上的点作角平分线的垂线
如图②,点P在∠MON的平分线上,若AP⊥OP,则延长AP交ON于点B.
结论:△AOB是等腰三角形,AP=BP,Rt△AOP≌Rt△BOP.
3.截长补短
情形1:已知点P是∠MON的平分线上一点,A是射线OM上任意一点(截长法).
结论:△OPB≌△OPA.
情形2:已知在△ABC中,AD平分∠BAC(补短法).
结论:△AFD≌△ACD.
方法二:作平行线构造等腰三角形
4.如图,在△ABC中,AD是∠BAC的平分线,E是AC边上的一点,连接DE,若∠BAC=30°,∠CED=120°,DE=1,则AE的长为 .
【解析】过点D作DF∥AB交AE于点F,易证AF=DF,∠EDF=90°,∠EFD=30°.
5.如图,在△ABC中,AB=5,BC=10,AD=2,BD平分∠ABC,则CD的长为 .
【解析】过点D作DE∥AB交BC于点E,易证BE=DE,由△CED∽△CBA求解.
4
【方法归纳】
1.过角平分线上的点作边的平行线
如图,点P在∠AOB的平分线上,过P作PQ∥OB交OA于点Q.
结论:OQ=PQ,△PQO是等腰三角形.
2.过边上的点作角平分线的平行线
如图,OC是∠AOB的平分线,D是OA上的一点,作DE∥OC交BO的延长线于点E.
结论:OD=OE,△EOD是等腰三角形.
B
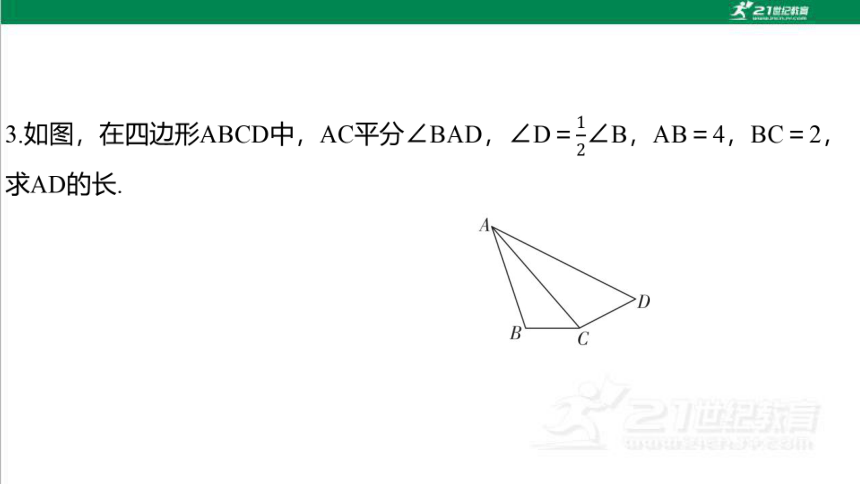
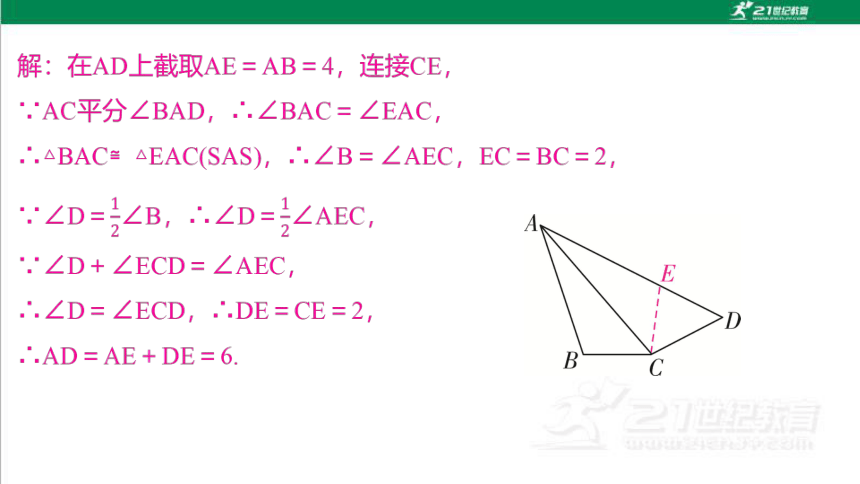
7.(2024·银川模拟)如图,在四边形ABCD中,对角线BD平分∠ABC,∠DCB=117°,∠ABC=50°,∠BAD+∠CAD=180°,那么∠DAC的度数为 .
【解析】延长BA和BC,过点D作DE⊥BA于点E,DF⊥BC 于点F,DG⊥AC于点G,判定AD为∠EAC的平分线,CD为∠ACF的平分线,即可得出∠DAC的度数.
52°
1
9.如图,已知∠AOB=30°,P是∠AOB平分线上一点,PD⊥OB,垂足为D,且PD=4,则OD的长为 .
【解析】过点P作PC∥OB交OA于点C,PE⊥OA于点E,∵OP是∠AOB的平分线,PD⊥OB,∴PE=PD=4, ∵CP∥OB,∠AOB=30°,∴∠ECP=∠AOB=30°,在Rt△ECP中,PC=2PE=8.
10.如图,在△ABC中,∠BAC=60°,∠B=80°,AD是∠BAC的平分线,求证:AC=AB+BD.
证明:在AC上截取AE=AB,连接DE,易得∠C=40°,
∵AD是∠BAC的平分线,∴∠BAD=∠CAD=30°,
∴△ABD≌△AED(SAS),∴∠ADB=∠ADE,BD=DE,
∵∠BAC=60°,∠B=80°,
∴∠ADE=∠ADB=∠CAD+∠C=70°,
∴∠CDE=180°-∠ADB-∠ADE=40°,
∴∠CDE=∠C,∴DE=CE,
∴AC=AE+CE=AE+DE=AB+BD,
∴AC=AB+BD.
方法一:利用角平分线性质构造对称图形
1.如图,在△ABC中,AD平分∠BAC,DE∥AB交AC于点E,CE=6,DE=5,过点D作DF⊥AB于点F,若DF=4,则△ACD的面积为( )
A.20
B.22
C.24
D.26
B
【方法归纳】
1.过角平分线上的点向角两边作垂线
如图①,点P在∠MON的平分线上,PA⊥OM,过点P作PB⊥ON于点B.
结论:AP=BP,Rt△AOP≌Rt△BOP.
2.如图,在△ABC中,AD平分∠BAC,AD⊥BD,E是BC的中点,连接DE,若AC=7,AB=3,则DE的长为 .
【解析】延长BD交AC于点H,证明△ADB≌△ADH,得BD=HD,AH=AB=3,求出CH,根据三角形中位线定理计算即可.
2
2.过角平分线上的点作角平分线的垂线
如图②,点P在∠MON的平分线上,若AP⊥OP,则延长AP交ON于点B.
结论:△AOB是等腰三角形,AP=BP,Rt△AOP≌Rt△BOP.
3.截长补短
情形1:已知点P是∠MON的平分线上一点,A是射线OM上任意一点(截长法).
结论:△OPB≌△OPA.
情形2:已知在△ABC中,AD平分∠BAC(补短法).
结论:△AFD≌△ACD.
方法二:作平行线构造等腰三角形
4.如图,在△ABC中,AD是∠BAC的平分线,E是AC边上的一点,连接DE,若∠BAC=30°,∠CED=120°,DE=1,则AE的长为 .
【解析】过点D作DF∥AB交AE于点F,易证AF=DF,∠EDF=90°,∠EFD=30°.
5.如图,在△ABC中,AB=5,BC=10,AD=2,BD平分∠ABC,则CD的长为 .
【解析】过点D作DE∥AB交BC于点E,易证BE=DE,由△CED∽△CBA求解.
4
【方法归纳】
1.过角平分线上的点作边的平行线
如图,点P在∠AOB的平分线上,过P作PQ∥OB交OA于点Q.
结论:OQ=PQ,△PQO是等腰三角形.
2.过边上的点作角平分线的平行线
如图,OC是∠AOB的平分线,D是OA上的一点,作DE∥OC交BO的延长线于点E.
结论:OD=OE,△EOD是等腰三角形.
B
7.(2024·银川模拟)如图,在四边形ABCD中,对角线BD平分∠ABC,∠DCB=117°,∠ABC=50°,∠BAD+∠CAD=180°,那么∠DAC的度数为 .
【解析】延长BA和BC,过点D作DE⊥BA于点E,DF⊥BC 于点F,DG⊥AC于点G,判定AD为∠EAC的平分线,CD为∠ACF的平分线,即可得出∠DAC的度数.
52°
1
9.如图,已知∠AOB=30°,P是∠AOB平分线上一点,PD⊥OB,垂足为D,且PD=4,则OD的长为 .
【解析】过点P作PC∥OB交OA于点C,PE⊥OA于点E,∵OP是∠AOB的平分线,PD⊥OB,∴PE=PD=4, ∵CP∥OB,∠AOB=30°,∴∠ECP=∠AOB=30°,在Rt△ECP中,PC=2PE=8.
10.如图,在△ABC中,∠BAC=60°,∠B=80°,AD是∠BAC的平分线,求证:AC=AB+BD.
证明:在AC上截取AE=AB,连接DE,易得∠C=40°,
∵AD是∠BAC的平分线,∴∠BAD=∠CAD=30°,
∴△ABD≌△AED(SAS),∴∠ADB=∠ADE,BD=DE,
∵∠BAC=60°,∠B=80°,
∴∠ADE=∠ADB=∠CAD+∠C=70°,
∴∠CDE=180°-∠ADB-∠ADE=40°,
∴∠CDE=∠C,∴DE=CE,
∴AC=AE+CE=AE+DE=AB+BD,
∴AC=AB+BD.
同课章节目录
