中考数学复习第五章四边形第二节矩形课件

(共17张PPT)
矩形的性质与判定
矩形的性质与判定
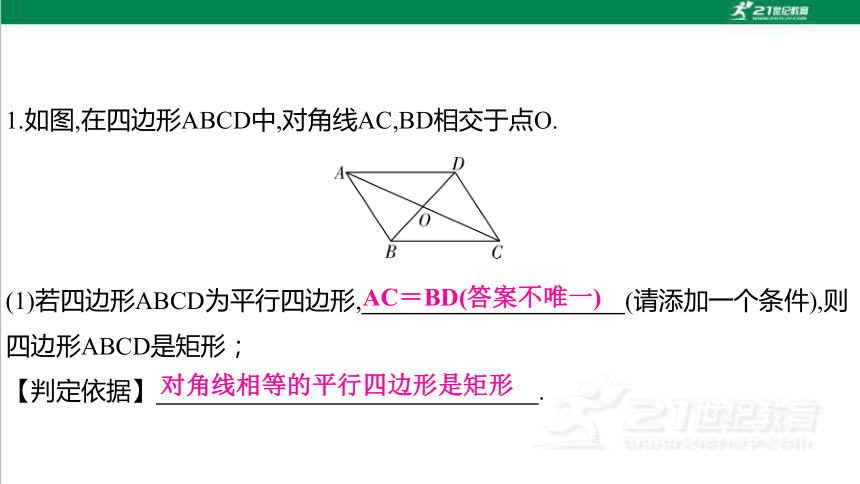
1.如图,在四边形ABCD中,对角线AC,BD相交于点O.
(1)若四边形ABCD为平行四边形, (请添加一个条件),则四边形ABCD是矩形；
【判定依据】 .
AC＝BD(答案不唯一)
对角线相等的平行四边形是矩形
(2)若四边形ABCD为一般四边形, (请添加一个条件),则四边形ABCD是矩形；
【判定依据】 .
∠DAB＝∠ABC＝∠BCD＝90°
有三个角是直角的四边形是矩形
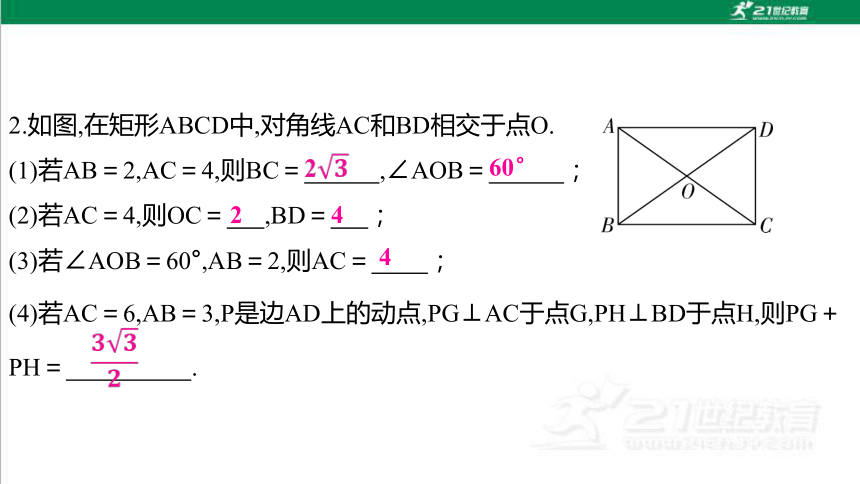
2.如图,在矩形ABCD中,对角线AC和BD相交于点O.
(1)若AB＝2,AC＝4,则BC＝ ,∠AOB＝ ；
(2)若AC＝4,则OC＝ ,BD＝ ；
(3)若∠AOB＝60°,AB＝2,则AC＝ ；
(4)若AC＝6,AB＝3,P是边AD上的动点,PG⊥AC于点G,PH⊥BD于点H,则PG＋PH＝ .

60°
2
4
4

重难点：矩形性质的相关证明与计算
如图①,已知四边形ABCD是矩形,点E在BA的延长线上,AE＝AD,EC与BD相交于点G,与AD相交于点F,AF＝AB.
(1)求证：BD⊥EC；
【思路点拨】证明△AEF≌△ADB(SAS),
则∠AEF＝∠ADB,∠GEB＋∠GBE＝
∠ADB＋∠ABD＝90°,即可求解.
证明：∵四边形ABCD是矩形,点E在BA的延长线上,
∴∠EAF＝∠DAB＝90°,
又∵AE＝AD,AF＝AB,
∴△AEF≌△ADB(SAS),
∴∠AEF＝∠ADB,
∴∠GEB＋∠GBE＝∠ADB＋∠ABD＝90°,
即∠EGB＝90°,∴BD⊥EC.


方法归纳：第(3)小题关键是根据图形特征,作辅助线构造手拉手全等模型探求几何线段之间的关系.(注：方法探究详见P81微专题(五)中手拉手全等模型)
(2024·潍坊)如图，在矩形ABCD中，AB＞2AD，点E，F分别在边AB，CD上．将△ADF沿AF折叠，点D的对应点G恰好落在对角线AC上；将△CBE沿CE折叠，点B的对应点H恰好也落在对角线AC上．连接GE，FH.
(1)求证：△AEH≌△CFG；
(2)求证：四边形EGFH为平行四边形．
证明：(1)∵四边形ABCD是矩形，
∴AD＝BC，∠B＝∠D＝90°，AB∥CD，
∴∠EAH＝∠FCG，
由折叠可得AG＝AD，CH＝CB，
∠CHE＝∠B＝90°，∠AGF＝∠D＝90°，
∴CH＝AG，∠AHE＝∠CGF＝90°，
∴AH＝CG，在△AEH和△CFG中，
∴△AEH≌△CFG(ASA)．
(2)由(1)知∠AHE＝∠CGF＝90°，
△AEH≌△CFG，
∴EH∥FG，EH＝FG，
∴四边形EGFH为平行四边形．