中考数学复习第五章四边形第一节平行四边形与多边形课件
文档属性
| 名称 | 中考数学复习第五章四边形第一节平行四边形与多边形课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 09:22:00 | ||
图片预览








文档简介
(共25张PPT)
多边形
多边形
平行四边形的性质和判定
平行四边形的性质和判定
1.已知凸n边形.
(1)若n边形的内角和是1 260°,则n= ;
(2)若这个n边形的内角和与外角和之比为3∶2,则n= ;
(3)若此n边形为正多边形,且每个外角都是36°,则它的内角和是 ;它共有 条对角线.
9
5
1 440°
35
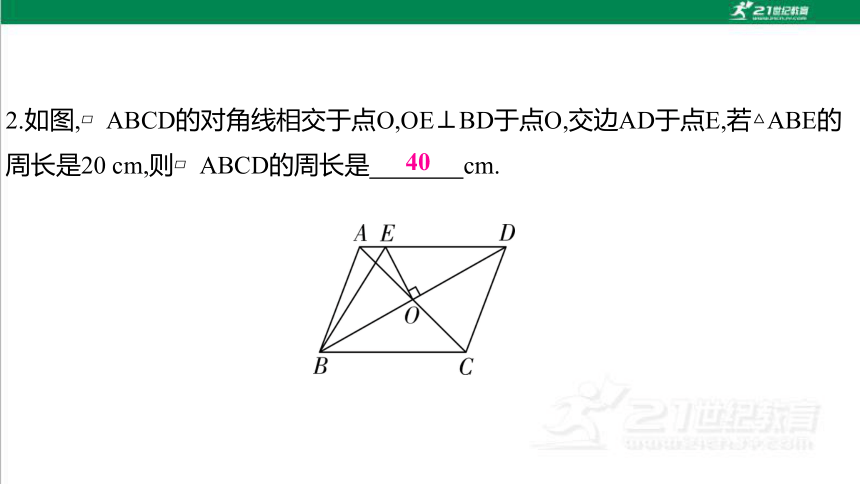
2.如图, ABCD的对角线相交于点O,OE⊥BD于点O,交边AD于点E,若△ABE的周长是20 cm,则 ABCD的周长是 cm.
40
3.四边形ABCD中,AB=CD,AD∥BC,则四边形ABCD 平行四边形(选填“是”或“不一定是”).
不一定是
4.如图,在 ABCD中,点E,F分别在CD,AB边上,连接EF,AC,相交于点O,请添加一个条件使四边形AFCE是平行四边形.
方法一:添加条件: ;
证明:∵四边形ABCD是平行四边形,∴AB∥CD.
∵EC=AF,∴四边形AFCE是平行四边形.
【判定依据】 .
EC=AF
有一组对边平行且相等的四边形是平行四边形
方法二:添加条件: ;
证明:∵四边形ABCD是平行四边形,∴AB∥CD.
又∵AE∥CF,∴四边形AFCE是平行四边形.
【判定依据】 .
AE∥CF
两组对边分别平行的四边形是平行四边形
方法三:添加条件: ;
证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠ECO=∠FAO,∠CEO=∠AFO,
又∵OE=OF,
∴△EOC≌△FOA(AAS),∴OA=OC,
∴四边形AFCE是平行四边形.
【判定依据】 .
OE=OF
对角线互相平分的四边形是平行四边形
方法四:添加条件: .
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠AEC+∠EAF=∠ECF+∠CFA=180°.
又∵∠DEA=∠BFC,∴∠AEC=∠CFA,
∴∠ECF=∠EAF,∴四边形AFCE是平行四边形.
【判定依据】 .
两组对角分别相等的四边形是平行四边形
∠DEA=∠BFC
重难点:平行四边形的相关证明与计算
如图,在平面直角坐标系中, ABCD的对角线的交点恰好与坐标原点重合,且点A,B的坐标分别为(2,3),(-3,3).(1)求点C,D的坐标;(2)求 ABCD的周长.
命题点1:正多边形的性质(近5年考查1次)
81°
1.(2024·宁夏第13题3分)如图,在正五边形ABCDE的内部,以CD边为边作正方形CDFH,连接BH,则∠BHC= .
命题点2:平行四边形的性质(近5年考查4次)
2.(2024·宁夏第21题6分)如图,在 ABCD中,点M,N在AD边上,AM=DN,连接CM并延长交BA的延长线于点E,连接BN并延长交CD的延长线于点F.求证:AE=DF.
小丽的思考过程如下:
参考小丽的思考过程,
完成推理.
命题点3:平行四边形的判定(近5年考查2次)
证明:∵EF∥AC,
∴∠EDC+∠C=180°,
又∵∠EDC=∠CBE,
∴∠CBE+∠C=180°,∴EB∥DC,
∵DE∥BC,BE∥CD,
∴四边形BCDE是平行四边形.
3.(2023·宁夏第19题6分)如图,已知EF∥AC,B,D分别是AC和EF上的点,∠EDC=∠CBE.求证:四边形BCDE是平行四边形.
多边形
多边形
平行四边形的性质和判定
平行四边形的性质和判定
1.已知凸n边形.
(1)若n边形的内角和是1 260°,则n= ;
(2)若这个n边形的内角和与外角和之比为3∶2,则n= ;
(3)若此n边形为正多边形,且每个外角都是36°,则它的内角和是 ;它共有 条对角线.
9
5
1 440°
35
2.如图, ABCD的对角线相交于点O,OE⊥BD于点O,交边AD于点E,若△ABE的周长是20 cm,则 ABCD的周长是 cm.
40
3.四边形ABCD中,AB=CD,AD∥BC,则四边形ABCD 平行四边形(选填“是”或“不一定是”).
不一定是
4.如图,在 ABCD中,点E,F分别在CD,AB边上,连接EF,AC,相交于点O,请添加一个条件使四边形AFCE是平行四边形.
方法一:添加条件: ;
证明:∵四边形ABCD是平行四边形,∴AB∥CD.
∵EC=AF,∴四边形AFCE是平行四边形.
【判定依据】 .
EC=AF
有一组对边平行且相等的四边形是平行四边形
方法二:添加条件: ;
证明:∵四边形ABCD是平行四边形,∴AB∥CD.
又∵AE∥CF,∴四边形AFCE是平行四边形.
【判定依据】 .
AE∥CF
两组对边分别平行的四边形是平行四边形
方法三:添加条件: ;
证明:∵四边形ABCD是平行四边形,∴AB∥CD,
∴∠ECO=∠FAO,∠CEO=∠AFO,
又∵OE=OF,
∴△EOC≌△FOA(AAS),∴OA=OC,
∴四边形AFCE是平行四边形.
【判定依据】 .
OE=OF
对角线互相平分的四边形是平行四边形
方法四:添加条件: .
证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠AEC+∠EAF=∠ECF+∠CFA=180°.
又∵∠DEA=∠BFC,∴∠AEC=∠CFA,
∴∠ECF=∠EAF,∴四边形AFCE是平行四边形.
【判定依据】 .
两组对角分别相等的四边形是平行四边形
∠DEA=∠BFC
重难点:平行四边形的相关证明与计算
如图,在平面直角坐标系中, ABCD的对角线的交点恰好与坐标原点重合,且点A,B的坐标分别为(2,3),(-3,3).(1)求点C,D的坐标;(2)求 ABCD的周长.
命题点1:正多边形的性质(近5年考查1次)
81°
1.(2024·宁夏第13题3分)如图,在正五边形ABCDE的内部,以CD边为边作正方形CDFH,连接BH,则∠BHC= .
命题点2:平行四边形的性质(近5年考查4次)
2.(2024·宁夏第21题6分)如图,在 ABCD中,点M,N在AD边上,AM=DN,连接CM并延长交BA的延长线于点E,连接BN并延长交CD的延长线于点F.求证:AE=DF.
小丽的思考过程如下:
参考小丽的思考过程,
完成推理.
命题点3:平行四边形的判定(近5年考查2次)
证明:∵EF∥AC,
∴∠EDC+∠C=180°,
又∵∠EDC=∠CBE,
∴∠CBE+∠C=180°,∴EB∥DC,
∵DE∥BC,BE∥CD,
∴四边形BCDE是平行四边形.
3.(2023·宁夏第19题6分)如图,已知EF∥AC,B,D分别是AC和EF上的点,∠EDC=∠CBE.求证:四边形BCDE是平行四边形.
同课章节目录
