中考数学复习第五章四边形第四节正方形课件

(共25张PPT)
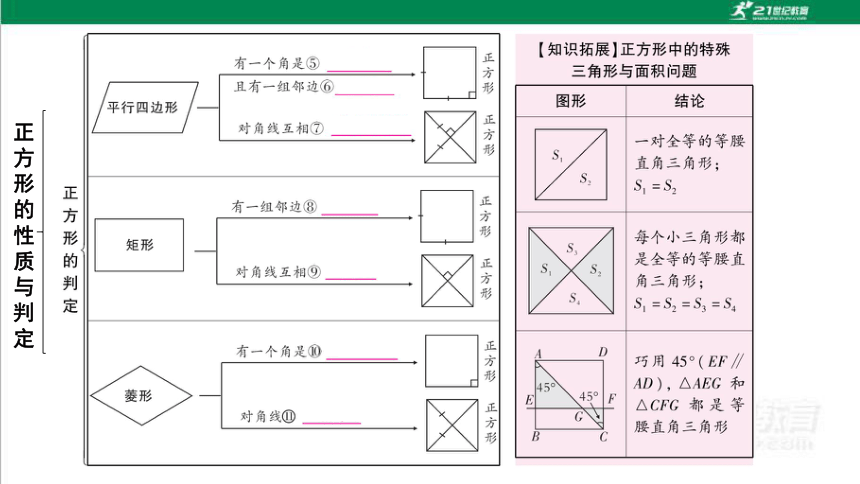
正方形的性质与判定
正方形的性质与判定
正方形的性质与判定
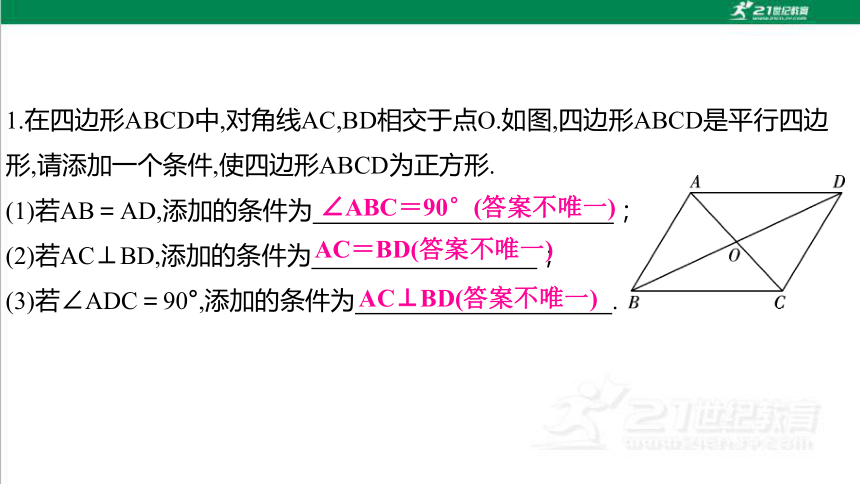
1.在四边形ABCD中,对角线AC,BD相交于点O.如图,四边形ABCD是平行四边形,请添加一个条件,使四边形ABCD为正方形.
(1)若AB＝AD,添加的条件为 ；
(2)若AC⊥BD,添加的条件为 ；
(3)若∠ADC＝90°,添加的条件为 .
∠ABC＝90°(答案不唯一)
AC＝BD(答案不唯一)
AC⊥BD(答案不唯一)
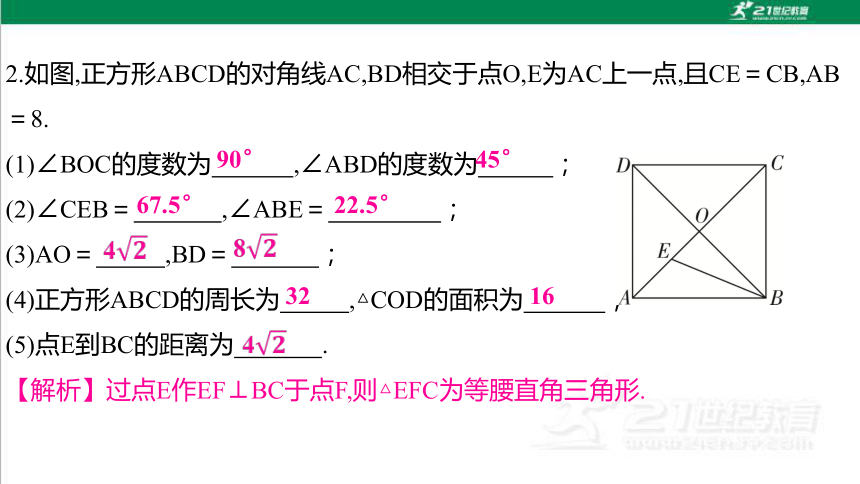
2.如图,正方形ABCD的对角线AC,BD相交于点O,E为AC上一点,且CE＝CB,AB＝8.
(1)∠BOC的度数为 ,∠ABD的度数为 ；
(2)∠CEB＝ ,∠ABE＝ ；
(3)AO＝ ,BD＝ ；
(4)正方形ABCD的周长为 ,△COD的面积为 ；
(5)点E到BC的距离为 .
【解析】过点E作EF⊥BC于点F,则△EFC为等腰直角三角形.
90°
45°
67.5°
22.5°

32
16


3.(数学拓展·七巧板)七巧板由五个等腰直角三角形与两个平行四边形(其中的一个平行四边形是正方形)组成,用七巧板可以拼出丰富多彩的图形,图中的正方形ABCD就是由七巧板拼成的,那么正方形EFGH的面积与正方形ABCD的面积的比值为 .

重难点：与正方形有关的证明与计算
[一题多角度]如图①,在正方形ABCD中,E是对角线AC上一动点,连接BE,DE.
(1)求证：△ABE≌△ADE；

(2)如图②,F是BC上一点,连接EF,若AB＝4,BF＝1,求△BEF周长的最小值；
【思路点拨】解题的关键是利用对称性把求△BEF的周长最小值转化为求BE＋EF′的最小值(F′为F关于AC的对称点).

(3)如图③,BE的延长线交AD于点G,交CD的延长线于点H,若EG·EH＝9,求DE的长；

(4)如图④,点F在BC延长线上,且EF＝DE,判断线段CD,CE,CF之间的数量关系,并写出证明过程.
【思路点拨】解题的关键是过点E作EG⊥CE,交BC于点G,证明△BEG≌△FEC.

命题点：正方形的性质(近5年考查4次，2021年与概率结合考查)
1．(2023·宁夏第10题3分)如图，在边长为2的正方形ABCD中，点E在AD上，连接EB，EC，则图中阴影部分的面积是 .
2
2．(2024·兰州)如图，四边形ABCD为正方形．△ADE为等边三角形，EF⊥AB于点F，若AD＝4，则EF＝ .
2
3．(2024·北京)如图，在正方形ABCD中，点E在AB上，AF⊥DE于点F，CG⊥DE于点G.若AD＝5，CG＝4，则△AEF的面积为 .


4．(2024·徐州)如图，四边形ABCD为正方形，点E在BD的延长线上，连接EA，EC.
(1)求证：△EAB≌△ECB；
(2)若∠AEC＝45°，求证：DC＝DE.
证明：(1)∵四边形ABCD为正方形，∴AB＝BC，∠ABE＝∠CBE＝45°，
在△EAB和△ECB中，
∴△EAB≌△ECB(SAS)．