2025年中考数学复习--第 44讲 圆与特殊四边形(含答案)
文档属性
| 名称 | 2025年中考数学复习--第 44讲 圆与特殊四边形(含答案) | 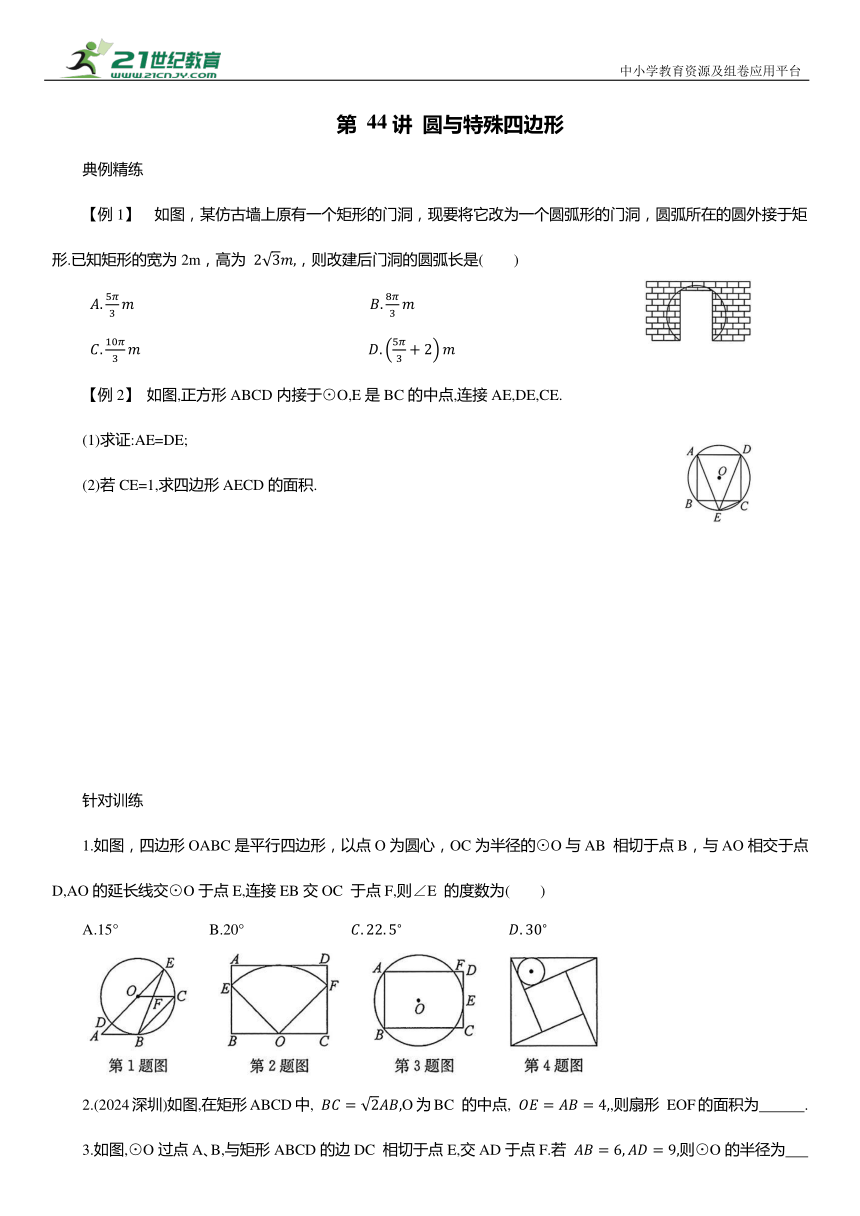 | |
| 格式 | docx | ||
| 文件大小 | 285.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 20:21:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第 44讲 圆与特殊四边形
典例精练
【例1】 如图,某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形.已知矩形的宽为2m,高为 ,则改建后门洞的圆弧长是( )
【例2】 如图,正方形ABCD内接于⊙O,E是BC的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
针对训练
1.如图,四边形OABC是平行四边形,以点O为圆心,OC为半径的⊙O与AB 相切于点B,与AO相交于点D,AO的延长线交⊙O于点E,连接EB交OC 于点F,则∠E 的度数为( )
A.15° B.20°
2.(2024深圳)如图,在矩形ABCD中, O为BC 的中点, ,则扇形 EOF的面积为 .
3.如图,⊙O过点A、B,与矩形ABCD的边DC 相切于点E,交AD于点F.若 则⊙O的半径为 .
4.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为 .
5.(2024 硚口)如图,在正方形ABCD铁皮上,以A为圆心剪下一个圆心角为90°的扇形,剩余部分剪一个半径为r的圆形,使之恰好围成一个圆锥.若 ,则r的最大值是 .
6.(2024 江汉)如图,已知四边形 ABCD中, ,以AB为直径作⊙O与边CD 相切于点E.
(1)如图1,连接BE,求证:∠ADC=2∠CBE;
(2)如图2,连接OD,OC交⊙O于点M.若OM=CM=2,求CD的长.
7.如图1, 的边AD 与经过A,B,C三点的⊙O相切.
(1)求证:
(2)如图2,延长DC交⊙O于点E,连接BE.若 求 tanD的值.
8.如图,AB是⊙O的直径, 于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点 F.
(1)求证:
(2)连接AF并延长,交⊙O于点G.填空:
①当 的度数为 时,四边形ECFG为菱形;
②当 的度数为 时,四边形 ECOG 为正方形.
9.如图,在 中, D为AC 上一点.以CD 为直径的⊙O与AB 相切于点E,交BC于点F, 垂足为G.
(1)求证:FG是⊙O的切线;
(2)若 求CF 的长.
第 44 讲 圆与特殊四边形
典例精练
【例1】 如图,某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形.已知矩形的宽为2m,高为 ,则改建后门洞的圆弧长是(C )
【例2】 如图,正方形ABCD内接于⊙O,E是BC的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
解:(1)证明:在正方形ABCD中,
∵E是BC的中点,. 即
(2)连接BD,作DF⊥DE于点D,交EC的延长线于点 F.
在正方形 ABCD中, 则∠F=45°,DE=DF,∠ADE=∠CDF.
∴△ADE≌△CDF(SAS).∴AE=CF,S△ADE=S△CDF.
∵EF= DE=CE+DE,CE=1,∴DE= +1.
针对训练
1.如图,四边形OABC是平行四边形,以点O为圆心,OC为半径的⊙O与AB 相切于点B,与AO相交于点D,AO的延长线交⊙O于点E,连接EB交OC 于点F,则 的度数为(C)
A.15° B.20°
2.(2024深圳)如图,在矩形ABCD中, ,O为BC的中点,OE=AB=4,则扇形 EOF的面积为 4π .
3.如图,⊙O过点A、B,与矩形ABCD的边DC相切于点E,交AD于点F.若AB=6,AD=9,则⊙O的半径为 5 .
4.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正
方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为 289 .
5.(2024 硚口)如图,在正方形ABCD铁皮上,以A为圆心剪下一个圆心角为90°的扇形,剩余部分剪一个半径为r的圆形,使之恰好围成一个圆锥.若 则r的最大值是 1 .
6.(2024江汉)如图,已知四边形 ABCD 中,∠DAB=∠ABC=90°,以AB为直径作⊙O与边CD 相切于点E.
(1)如图1,连接BE,求证:∠ADC=2∠CBE;
(2)如图2,连接OD,OC交⊙O于点M.若OM=CM=2,求CD的长.
解:(1)证明:∵∠DAB=∠ABC=90°,且点 B在⊙O上,
∴BC是⊙O的切线,且AD∥BC.又∵⊙O与边CD 相切,
又∵
即∠ADC=2∠CBE.
(2)连接OE,则∠OAD=∠OED=∠OBC=∠OEC=90°,易得△OAD≌△OED,△COE≌△COB,
∴∠AOD=∠EOD,∠COE=∠COB.∴∠COD=90°.
∵OM=CM=OE=2,∴CE=2 ,∠OCE=30°.
7.如图1, ABCD的边AD 与经过A,B,C三点的⊙O相切.
(1)求证:
(2)如图2,延长DC交⊙O于点E,连接BE.若 求 tanD的值.
解:(1)证明:连接OA交BC于点 F.
∵四边形 ABCD是平行四边形,
∴AD∥BC.∴∠OAD=∠OFC.
∵AD与⊙O相切,∴∠OAD=90.∴∠OFC=90.
∴OA 平分BC,即
(2)分别过A,B两点作DE的垂线,垂足分别为N,M,连接AC.
∵四边形 ABCD是平行四边形,∵
∵AB=AC,∴BE=AC=AB.∴BE=AB=AC,AE=CB.,∴∠E=∠ACN.
由 设AC=BE=13m,则BM=12m,EM=5m,AN=12m,CN=5m.
∵BM∥AN且BM=AN,∴四边形 BMNA 是平行四边形,∴MN=AB=13m.∴CM=18m.
8.如图,AB是⊙O的直径,DO⊥AB于点O,连接DA 交⊙O于点C,过点 C作⊙O的切线交DO于点E,连接BC交DO于点F.
(1)求证:CE=EF;
(2)连接AF并延长,交⊙O于点G.填空:
①当∠D 的度数为 30° 时,四边形ECFG为菱形;
②当∠D 的度数为 22.5° 时,四边形 ECOG为正方形.
解:(1)证明:连接OC.∵CE为⊙O的切线,∴OC⊥CE.
∴∠OCE=90°,即
∵DO⊥AB,∴∠OFB+∠B=90°.
∵∠CFE=∠OFB,∴∠CFE+∠B=90°.
又∵OB=OC,∴∠FCO=∠B.
∴∠FCE=∠CFE.∴CE=EF.
9.如图,在△ABC中,AB=AC,D为AC上一点.以CD为直径的⊙O与AB 相切于点E,交BC于点F,FG⊥AB,垂足为G.
(1)求证:FG是⊙O的切线;
(2)若BG=1,BF=3,求CF的长.
解:(1)证明:连接DF,OF,易证∠BFG=∠DFO,得∠GFO=∠BFD=90°.
又∵OF是⊙O的半径,∴FG是⊙O的切线.
(2)连接OE.∵AB是⊙O的切线,∴OE⊥AB.
又∵OF⊥FG,FG⊥AB,∴四边形GEOF 是矩形.
∵OE=OF,∴四边形GEOF 是正方形.
∵BG=1,BF=3,∴GF=OE=2
设∠BFG=∠FDC=β.∵FG⊥AB,DF⊥CF,∴sinβ=β==BC
解得
第 44讲 圆与特殊四边形
典例精练
【例1】 如图,某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形.已知矩形的宽为2m,高为 ,则改建后门洞的圆弧长是( )
【例2】 如图,正方形ABCD内接于⊙O,E是BC的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
针对训练
1.如图,四边形OABC是平行四边形,以点O为圆心,OC为半径的⊙O与AB 相切于点B,与AO相交于点D,AO的延长线交⊙O于点E,连接EB交OC 于点F,则∠E 的度数为( )
A.15° B.20°
2.(2024深圳)如图,在矩形ABCD中, O为BC 的中点, ,则扇形 EOF的面积为 .
3.如图,⊙O过点A、B,与矩形ABCD的边DC 相切于点E,交AD于点F.若 则⊙O的半径为 .
4.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为 .
5.(2024 硚口)如图,在正方形ABCD铁皮上,以A为圆心剪下一个圆心角为90°的扇形,剩余部分剪一个半径为r的圆形,使之恰好围成一个圆锥.若 ,则r的最大值是 .
6.(2024 江汉)如图,已知四边形 ABCD中, ,以AB为直径作⊙O与边CD 相切于点E.
(1)如图1,连接BE,求证:∠ADC=2∠CBE;
(2)如图2,连接OD,OC交⊙O于点M.若OM=CM=2,求CD的长.
7.如图1, 的边AD 与经过A,B,C三点的⊙O相切.
(1)求证:
(2)如图2,延长DC交⊙O于点E,连接BE.若 求 tanD的值.
8.如图,AB是⊙O的直径, 于点O,连接DA交⊙O于点C,过点C作⊙O的切线交DO于点E,连接BC交DO于点 F.
(1)求证:
(2)连接AF并延长,交⊙O于点G.填空:
①当 的度数为 时,四边形ECFG为菱形;
②当 的度数为 时,四边形 ECOG 为正方形.
9.如图,在 中, D为AC 上一点.以CD 为直径的⊙O与AB 相切于点E,交BC于点F, 垂足为G.
(1)求证:FG是⊙O的切线;
(2)若 求CF 的长.
第 44 讲 圆与特殊四边形
典例精练
【例1】 如图,某仿古墙上原有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接于矩形.已知矩形的宽为2m,高为 ,则改建后门洞的圆弧长是(C )
【例2】 如图,正方形ABCD内接于⊙O,E是BC的中点,连接AE,DE,CE.
(1)求证:AE=DE;
(2)若CE=1,求四边形AECD的面积.
解:(1)证明:在正方形ABCD中,
∵E是BC的中点,. 即
(2)连接BD,作DF⊥DE于点D,交EC的延长线于点 F.
在正方形 ABCD中, 则∠F=45°,DE=DF,∠ADE=∠CDF.
∴△ADE≌△CDF(SAS).∴AE=CF,S△ADE=S△CDF.
∵EF= DE=CE+DE,CE=1,∴DE= +1.
针对训练
1.如图,四边形OABC是平行四边形,以点O为圆心,OC为半径的⊙O与AB 相切于点B,与AO相交于点D,AO的延长线交⊙O于点E,连接EB交OC 于点F,则 的度数为(C)
A.15° B.20°
2.(2024深圳)如图,在矩形ABCD中, ,O为BC的中点,OE=AB=4,则扇形 EOF的面积为 4π .
3.如图,⊙O过点A、B,与矩形ABCD的边DC相切于点E,交AD于点F.若AB=6,AD=9,则⊙O的半径为 5 .
4.我国古代数学家赵爽的“弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正
方形(如图所示).若直角三角形的内切圆半径为3,小正方形的面积为49,则大正方形的面积为 289 .
5.(2024 硚口)如图,在正方形ABCD铁皮上,以A为圆心剪下一个圆心角为90°的扇形,剩余部分剪一个半径为r的圆形,使之恰好围成一个圆锥.若 则r的最大值是 1 .
6.(2024江汉)如图,已知四边形 ABCD 中,∠DAB=∠ABC=90°,以AB为直径作⊙O与边CD 相切于点E.
(1)如图1,连接BE,求证:∠ADC=2∠CBE;
(2)如图2,连接OD,OC交⊙O于点M.若OM=CM=2,求CD的长.
解:(1)证明:∵∠DAB=∠ABC=90°,且点 B在⊙O上,
∴BC是⊙O的切线,且AD∥BC.又∵⊙O与边CD 相切,
又∵
即∠ADC=2∠CBE.
(2)连接OE,则∠OAD=∠OED=∠OBC=∠OEC=90°,易得△OAD≌△OED,△COE≌△COB,
∴∠AOD=∠EOD,∠COE=∠COB.∴∠COD=90°.
∵OM=CM=OE=2,∴CE=2 ,∠OCE=30°.
7.如图1, ABCD的边AD 与经过A,B,C三点的⊙O相切.
(1)求证:
(2)如图2,延长DC交⊙O于点E,连接BE.若 求 tanD的值.
解:(1)证明:连接OA交BC于点 F.
∵四边形 ABCD是平行四边形,
∴AD∥BC.∴∠OAD=∠OFC.
∵AD与⊙O相切,∴∠OAD=90.∴∠OFC=90.
∴OA 平分BC,即
(2)分别过A,B两点作DE的垂线,垂足分别为N,M,连接AC.
∵四边形 ABCD是平行四边形,∵
∵AB=AC,∴BE=AC=AB.∴BE=AB=AC,AE=CB.,∴∠E=∠ACN.
由 设AC=BE=13m,则BM=12m,EM=5m,AN=12m,CN=5m.
∵BM∥AN且BM=AN,∴四边形 BMNA 是平行四边形,∴MN=AB=13m.∴CM=18m.
8.如图,AB是⊙O的直径,DO⊥AB于点O,连接DA 交⊙O于点C,过点 C作⊙O的切线交DO于点E,连接BC交DO于点F.
(1)求证:CE=EF;
(2)连接AF并延长,交⊙O于点G.填空:
①当∠D 的度数为 30° 时,四边形ECFG为菱形;
②当∠D 的度数为 22.5° 时,四边形 ECOG为正方形.
解:(1)证明:连接OC.∵CE为⊙O的切线,∴OC⊥CE.
∴∠OCE=90°,即
∵DO⊥AB,∴∠OFB+∠B=90°.
∵∠CFE=∠OFB,∴∠CFE+∠B=90°.
又∵OB=OC,∴∠FCO=∠B.
∴∠FCE=∠CFE.∴CE=EF.
9.如图,在△ABC中,AB=AC,D为AC上一点.以CD为直径的⊙O与AB 相切于点E,交BC于点F,FG⊥AB,垂足为G.
(1)求证:FG是⊙O的切线;
(2)若BG=1,BF=3,求CF的长.
解:(1)证明:连接DF,OF,易证∠BFG=∠DFO,得∠GFO=∠BFD=90°.
又∵OF是⊙O的半径,∴FG是⊙O的切线.
(2)连接OE.∵AB是⊙O的切线,∴OE⊥AB.
又∵OF⊥FG,FG⊥AB,∴四边形GEOF 是矩形.
∵OE=OF,∴四边形GEOF 是正方形.
∵BG=1,BF=3,∴GF=OE=2
设∠BFG=∠FDC=β.∵FG⊥AB,DF⊥CF,∴sinβ=β==BC
解得
同课章节目录
