2025年中考数学复习--第34 讲 无网格无刻度直尺画图(含答案)
文档属性
| 名称 | 2025年中考数学复习--第34 讲 无网格无刻度直尺画图(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 339.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 20:33:57 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第34 讲 无网格无刻度直尺画图
典例精练
【例1】 (1)如图1,P是平行四边形ABCD 的边AD 上一点,过点 P 画一条直线把这个四边形分成面积相等的两部分;
(2)如图2,五边形ABCDE 是正五边形,画一条直线把这个五边形分成面积相等的两部分;
(3)如图3,△ABC的外接圆的圆心是点O,D是AC的中点,画一条直线把△ABC分成面积相等的两部分.
【例2】 只用无刻度的直尺作图(保留作图痕迹,不要求写作法).
(1)如图1,已知∠AOB,OA=OB,点E在边OB 上,四边形AEBF 是平行四边形,请你在图中画出∠AOB 的平分线;
(2)如图2,在矩形ABCD中,E,F分别是AB 和AD 的中点,以EF 为边画一个菱形.
针对训练
1.(1)如图1,在 ABCD中,点M在边BC上,在AD上求作一点N,使AN=MC;
(2)如图2,在菱形ABCD中,点M在边BC上,在CD上求作一点E,使CE=MC.
2.如图,在菱形ABCD中,E为AB的中点,请仅用无刻度的直尺作图(保留作图痕迹,不写作法).
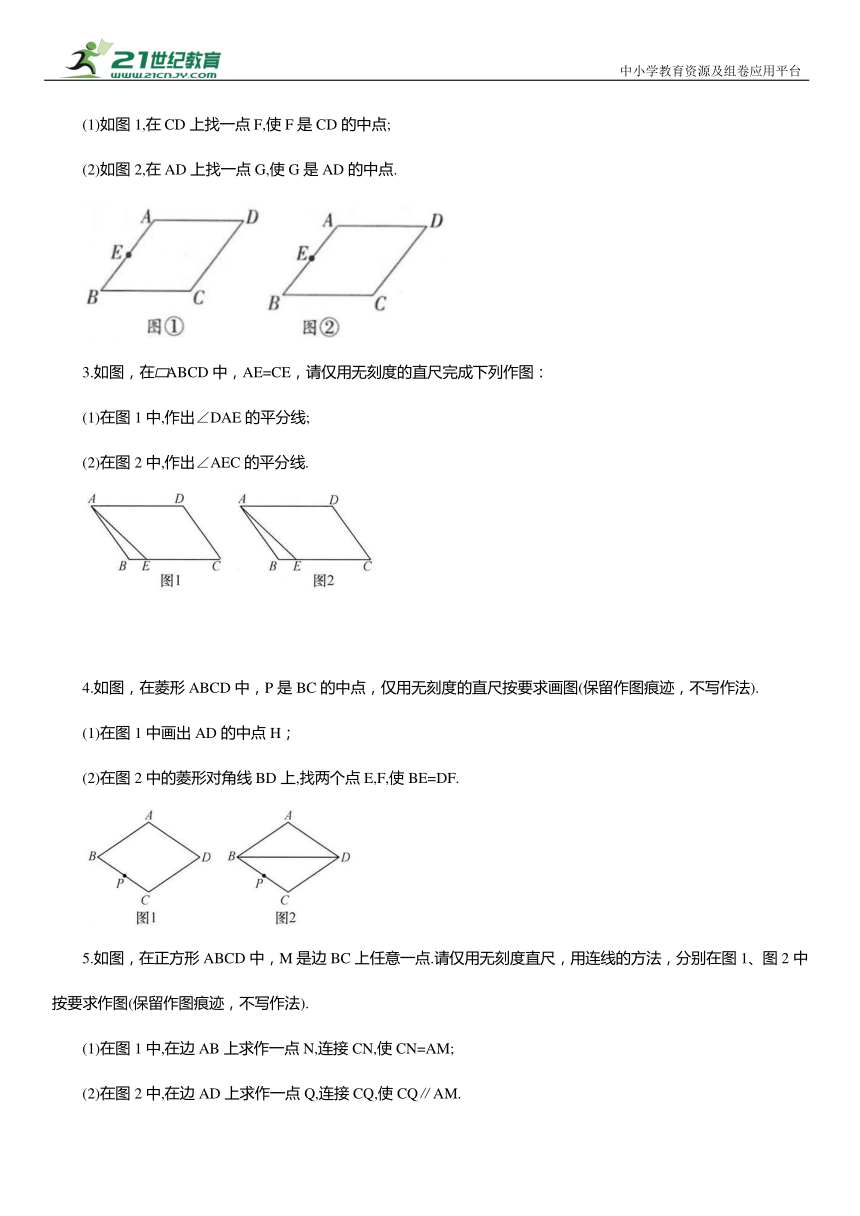
(1)如图1,在CD上找一点F,使F是CD的中点;
(2)如图2,在AD上找一点G,使G是AD的中点.
3.如图,在 ABCD中,AE=CE,请仅用无刻度的直尺完成下列作图:
(1)在图1中,作出∠DAE的平分线;
(2)在图2中,作出∠AEC的平分线.
4.如图,在菱形ABCD中,P是BC的中点,仅用无刻度的直尺按要求画图(保留作图痕迹,不写作法).
(1)在图1中画出AD的中点H;
(2)在图2中的菱形对角线BD上,找两个点E,F,使BE=DF.
5.如图,在正方形ABCD中,M是边BC上任意一点.请仅用无刻度直尺,用连线的方法,分别在图1、图2中按要求作图(保留作图痕迹,不写作法).
(1)在图1中,在边AB上求作一点N,连接CN,使CN=AM;
(2)在图2中,在边AD上求作一点Q,连接CQ,使CQ∥AM.
6.如图,已知正七边形 ABCDEFG.
(1)画一个以 AB 为边的平行四边形;
(2)画一个以AF为边的菱形.
第34讲 无网格无刻度直尺画图
典例精练
【例1】 (1)如图1,P是平行四边形ABCD的边AD上一点,过点P 画一条直线把这个四边形分成面积相等的两部分;
(2)如图2,五边形ABCDE是正五边形,画一条直线把这个五边形分成面积相等的两部分;
(3)如图3,△ABC的外接圆的圆心是点O,D是AC的中点,画一条直线把△ABC分成面积相等的两部分.
【例2】 只用无刻度的直尺作图(保留作图痕迹,不要求写作法).
(1)如图1,已知∠AOB,OA=OB,点E在边OB 上,四边形AEBF 是平行四边形,请你在图中画出∠AOB 的平分线;
(2)如图2,在矩形ABCD中,E,F分别是AB 和AD 的中点,以EF 为边画一个菱形.
解:(1)射线OP 即为所求.(2)四边形 EFGH 即为所求的菱形.
针对训练
1.(1)如图1,在 ABCD中,点M在边BC上,在AD上求作一点N,使AN=MC;
(2)如图2,在菱形ABCD中,点M在边BC上,在CD上求作一点E,使CE=MC.
2.如图,在菱形ABCD中,E为AB的中点,请仅用无刻度的直尺作图(保留作图痕迹,不写作法).
(1)如图1,在CD上找一点F,使F是CD的中点;
(2)如图2,在AD上找一点G,使G是AD的中点.
3.如图,在 ABCD中,AE=CE,请仅用无刻度的直尺完成下列作图:
(1)在图1中,作出∠DAE的平分线;
(2)在图2中,作出∠AEC的平分线.
解:(1)连线AC,AC即为∠DAE的平分线.
(2)①连接AC,BD交于点O,②作射线EO,EO为∠AEC的平分线.
4.如图,在菱形ABCD中,P是BC的中点,仅用无刻度的直尺按要求画图(保留作图痕迹,不写作法).
(1)在图1中画出AD的中点H;
(2)在图2中的菱形对角线BD上,找两个点 E,F,使BE=DF.
5.如图,在正方形ABCD中,M是边BC上任意一点.请仅用无刻度直尺,用连线的方法,分别在图1、图2中按要求作图(保留作图痕迹,不写作法).
(1)在图1中,在边AB上求作一点N,连接CN,使CN=AM;
(2)在图2中,在边AD上求作一点Q,连接CQ,使CQ∥AM.
6.如图,已知正七边形 ABCDEFG.
(1)画一个以 AB 为边的平行四边形;
(2)画一个以AF 为边的菱形.
解:(1) ABHF 即为所求.(2)菱形AFDH 即为所求.
第34 讲 无网格无刻度直尺画图
典例精练
【例1】 (1)如图1,P是平行四边形ABCD 的边AD 上一点,过点 P 画一条直线把这个四边形分成面积相等的两部分;
(2)如图2,五边形ABCDE 是正五边形,画一条直线把这个五边形分成面积相等的两部分;
(3)如图3,△ABC的外接圆的圆心是点O,D是AC的中点,画一条直线把△ABC分成面积相等的两部分.
【例2】 只用无刻度的直尺作图(保留作图痕迹,不要求写作法).
(1)如图1,已知∠AOB,OA=OB,点E在边OB 上,四边形AEBF 是平行四边形,请你在图中画出∠AOB 的平分线;
(2)如图2,在矩形ABCD中,E,F分别是AB 和AD 的中点,以EF 为边画一个菱形.
针对训练
1.(1)如图1,在 ABCD中,点M在边BC上,在AD上求作一点N,使AN=MC;
(2)如图2,在菱形ABCD中,点M在边BC上,在CD上求作一点E,使CE=MC.
2.如图,在菱形ABCD中,E为AB的中点,请仅用无刻度的直尺作图(保留作图痕迹,不写作法).
(1)如图1,在CD上找一点F,使F是CD的中点;
(2)如图2,在AD上找一点G,使G是AD的中点.
3.如图,在 ABCD中,AE=CE,请仅用无刻度的直尺完成下列作图:
(1)在图1中,作出∠DAE的平分线;
(2)在图2中,作出∠AEC的平分线.
4.如图,在菱形ABCD中,P是BC的中点,仅用无刻度的直尺按要求画图(保留作图痕迹,不写作法).
(1)在图1中画出AD的中点H;
(2)在图2中的菱形对角线BD上,找两个点E,F,使BE=DF.
5.如图,在正方形ABCD中,M是边BC上任意一点.请仅用无刻度直尺,用连线的方法,分别在图1、图2中按要求作图(保留作图痕迹,不写作法).
(1)在图1中,在边AB上求作一点N,连接CN,使CN=AM;
(2)在图2中,在边AD上求作一点Q,连接CQ,使CQ∥AM.
6.如图,已知正七边形 ABCDEFG.
(1)画一个以 AB 为边的平行四边形;
(2)画一个以AF为边的菱形.
第34讲 无网格无刻度直尺画图
典例精练
【例1】 (1)如图1,P是平行四边形ABCD的边AD上一点,过点P 画一条直线把这个四边形分成面积相等的两部分;
(2)如图2,五边形ABCDE是正五边形,画一条直线把这个五边形分成面积相等的两部分;
(3)如图3,△ABC的外接圆的圆心是点O,D是AC的中点,画一条直线把△ABC分成面积相等的两部分.
【例2】 只用无刻度的直尺作图(保留作图痕迹,不要求写作法).
(1)如图1,已知∠AOB,OA=OB,点E在边OB 上,四边形AEBF 是平行四边形,请你在图中画出∠AOB 的平分线;
(2)如图2,在矩形ABCD中,E,F分别是AB 和AD 的中点,以EF 为边画一个菱形.
解:(1)射线OP 即为所求.(2)四边形 EFGH 即为所求的菱形.
针对训练
1.(1)如图1,在 ABCD中,点M在边BC上,在AD上求作一点N,使AN=MC;
(2)如图2,在菱形ABCD中,点M在边BC上,在CD上求作一点E,使CE=MC.
2.如图,在菱形ABCD中,E为AB的中点,请仅用无刻度的直尺作图(保留作图痕迹,不写作法).
(1)如图1,在CD上找一点F,使F是CD的中点;
(2)如图2,在AD上找一点G,使G是AD的中点.
3.如图,在 ABCD中,AE=CE,请仅用无刻度的直尺完成下列作图:
(1)在图1中,作出∠DAE的平分线;
(2)在图2中,作出∠AEC的平分线.
解:(1)连线AC,AC即为∠DAE的平分线.
(2)①连接AC,BD交于点O,②作射线EO,EO为∠AEC的平分线.
4.如图,在菱形ABCD中,P是BC的中点,仅用无刻度的直尺按要求画图(保留作图痕迹,不写作法).
(1)在图1中画出AD的中点H;
(2)在图2中的菱形对角线BD上,找两个点 E,F,使BE=DF.
5.如图,在正方形ABCD中,M是边BC上任意一点.请仅用无刻度直尺,用连线的方法,分别在图1、图2中按要求作图(保留作图痕迹,不写作法).
(1)在图1中,在边AB上求作一点N,连接CN,使CN=AM;
(2)在图2中,在边AD上求作一点Q,连接CQ,使CQ∥AM.
6.如图,已知正七边形 ABCDEFG.
(1)画一个以 AB 为边的平行四边形;
(2)画一个以AF 为边的菱形.
解:(1) ABHF 即为所求.(2)菱形AFDH 即为所求.
同课章节目录
