2025年中考数学复习--第35 讲 圆中角度计算(含答案)
文档属性
| 名称 | 2025年中考数学复习--第35 讲 圆中角度计算(含答案) | 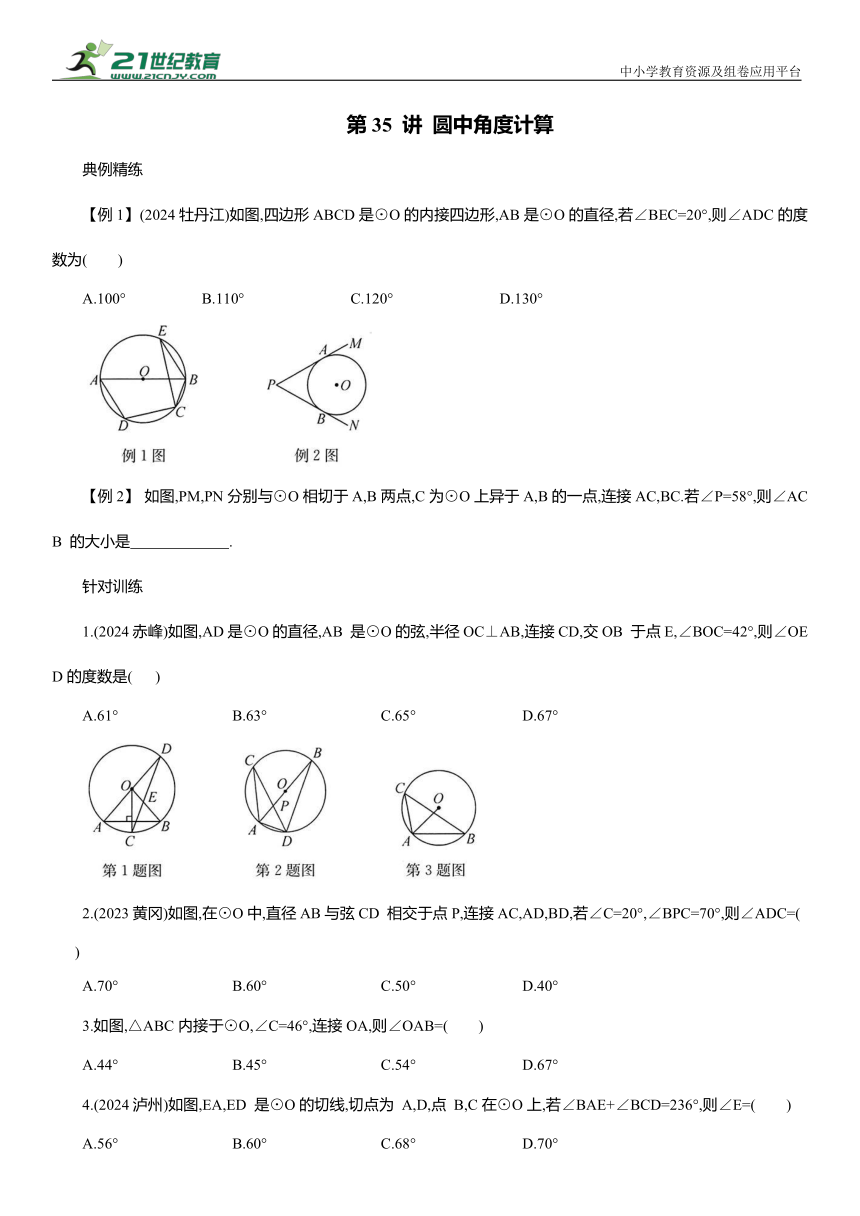 | |
| 格式 | docx | ||
| 文件大小 | 311.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 20:36:30 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第35 讲 圆中角度计算
典例精练
【例1】 (2024牡丹江)如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若∠BEC=20°,则∠ADC的度数为( )
A.100° B.110° C.120° D.130°
【例2】 如图,PM,PN分别与⊙O相切于A,B两点,C为⊙O上异于A,B的一点,连接AC,BC.若∠P=58°,则∠ACB 的大小是 .
针对训练
1.(2024赤峰)如图,AD是⊙O的直径,AB 是⊙O的弦,半径OC⊥AB,连接CD,交OB 于点E,∠BOC=42°,则∠OED的度数是( )
A.61° B.63° C.65° D.67°
2.(2023黄冈)如图,在⊙O中,直径AB与弦CD 相交于点P,连接AC,AD,BD,若∠C=20°,∠BPC=70°,则∠ADC=( )
A.70° B.60° C.50° D.40°
3.如图,△ABC内接于⊙O,∠C=46°,连接OA,则∠OAB=( )
A.44° B.45° C.54° D.67°
4.(2024泸州)如图,EA,ED 是⊙O的切线,切点为 A,D,点 B,C在⊙O上,若∠BAE+∠BCD=236°,则∠E=( )
A.56° B.60° C.68° D.70°
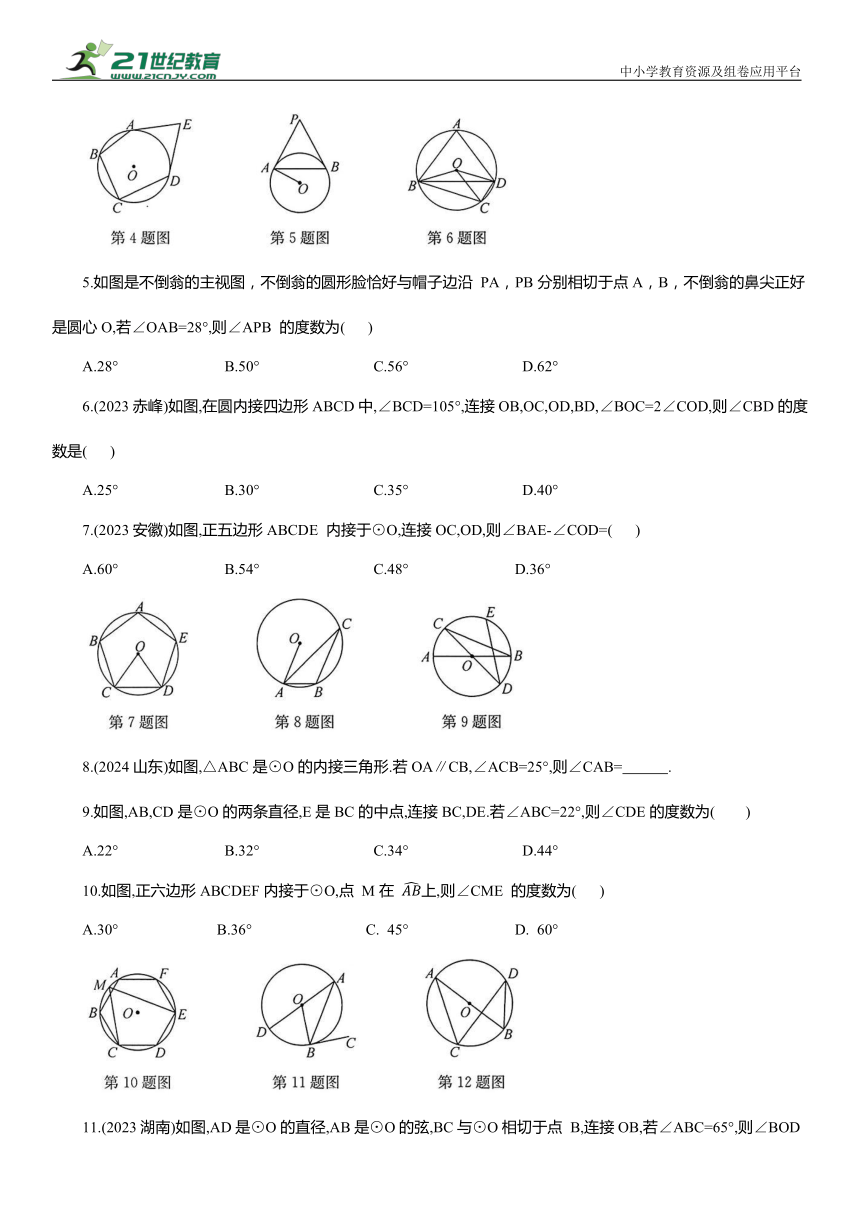
5.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿 PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB 的度数为( )
A.28° B.50° C.56° D.62°
6.(2023赤峰)如图,在圆内接四边形ABCD中,∠BCD=105°,连接OB,OC,OD,BD,∠BOC=2∠COD,则∠CBD的度数是( )
A.25° B.30° C.35° D.40°
7.(2023安徽)如图,正五边形ABCDE 内接于⊙O,连接OC,OD,则∠BAE-∠COD=( )
A.60° B.54° C.48° D.36°
8.(2024山东)如图,△ABC是⊙O的内接三角形.若OA∥CB,∠ACB=25°,则∠CAB= .
9.如图,AB,CD是⊙O的两条直径,E是BC的中点,连接BC,DE.若∠ABC=22°,则∠CDE的度数为( )
A.22° B.32° C.34° D.44°
10.如图,正六边形ABCDEF内接于⊙O,点 M在 上,则∠CME 的度数为( )
A.30° B.36° C. 45° D. 60°
11.(2023湖南)如图,AD是⊙O的直径,AB是⊙O的弦,BC与⊙O相切于点 B,连接OB,若∠ABC=65°,则∠BOD 的大小为 .
12.(2024北京)如图,⊙O的直径AB 平分弦CD(不是直径).若∠D=35°,则∠C= °.
第35 讲 圆中角度计算
典例精练
【例1】 (2024牡丹江)如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若∠BEC=20°,则∠ADC的度数为( B)
A.100° B.110° C.120° D.130°
【例2】 如图,PM,PN分别与⊙O相切于A,B两点,C为⊙O上异于A,B的一点,连接AC,BC.若∠P=58°,则∠ACB 的大小是 61°或119° .
针对训练
1.(2024赤峰)如图,AD是⊙O的直径,AB 是⊙O的弦,半径OC⊥AB,连接CD,交OB 于点E,∠BOC=42°,则∠OED 的度数是(B )
A.61° B.63° C.65° D.67°
2.(2023黄冈)如图,在⊙O中,直径AB与弦CD 相交于点 P,连接AC,AD,BD,若∠C=20°,∠BPC=70°,则∠ADC=(D )
A.70° B.60° C.50° D.40°
3.如图,△ABC内接于⊙O,∠C=46°,连接OA,则∠OAB=(A )
A.44° B.45° C.54° D.67°
4.(2024泸州)如图,EA,ED 是⊙O的切线,切点为 A,D,点 B,C在⊙O上,若∠BAE+∠BCD=236°,则∠E=( C )
A.56° B.60° C.68° D.70°
5.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿 PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB 的度数为(C)
A.28° B.50° C.56° D.62°
6.(2023赤峰)如图,在圆内接四边形 ABCD中,∠BCD=105°,连接OB,OC,OD,BD,∠BOC=2∠COD,则∠CBD的度数是(A)
A.25° B.30° C.35° D.40°
7.(2023安徽)如图,正五边形ABCDE 内接于⊙O,连接OC,OD,则∠BAE-∠COD=(D)
A.60° B.54° C.48° D.36°
8.(2024山东)如图,△ABC是⊙O的内接三角形.若OA∥CB,∠ACB=25°,则∠CAB= 40°.
9.如图,AB,CD是⊙O的两条直径,E是BC的中点,连接BC,DE.若∠ABC=22°,则∠CDE的度数为(C)
A.22° B.32° C.34° D.44°
10.如图,正六边形ABCDEF 内接于⊙O,点 M在 上,则∠CME的度数为(D)
A.30° B.36° C. 45° D. 60°
11.(2023湖南)如图,AD是⊙O的直径,AB是⊙O的弦,BC与⊙O相切于点B,连接OB,若∠ABC=65°,则∠BOD 的大小为 50° .
12.(2024北京)如图,⊙O的直径AB平分弦CD(不是直径).若∠D=35°,则∠C= 55 °.
第35 讲 圆中角度计算
典例精练
【例1】 (2024牡丹江)如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若∠BEC=20°,则∠ADC的度数为( )
A.100° B.110° C.120° D.130°
【例2】 如图,PM,PN分别与⊙O相切于A,B两点,C为⊙O上异于A,B的一点,连接AC,BC.若∠P=58°,则∠ACB 的大小是 .
针对训练
1.(2024赤峰)如图,AD是⊙O的直径,AB 是⊙O的弦,半径OC⊥AB,连接CD,交OB 于点E,∠BOC=42°,则∠OED的度数是( )
A.61° B.63° C.65° D.67°
2.(2023黄冈)如图,在⊙O中,直径AB与弦CD 相交于点P,连接AC,AD,BD,若∠C=20°,∠BPC=70°,则∠ADC=( )
A.70° B.60° C.50° D.40°
3.如图,△ABC内接于⊙O,∠C=46°,连接OA,则∠OAB=( )
A.44° B.45° C.54° D.67°
4.(2024泸州)如图,EA,ED 是⊙O的切线,切点为 A,D,点 B,C在⊙O上,若∠BAE+∠BCD=236°,则∠E=( )
A.56° B.60° C.68° D.70°
5.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿 PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB 的度数为( )
A.28° B.50° C.56° D.62°
6.(2023赤峰)如图,在圆内接四边形ABCD中,∠BCD=105°,连接OB,OC,OD,BD,∠BOC=2∠COD,则∠CBD的度数是( )
A.25° B.30° C.35° D.40°
7.(2023安徽)如图,正五边形ABCDE 内接于⊙O,连接OC,OD,则∠BAE-∠COD=( )
A.60° B.54° C.48° D.36°
8.(2024山东)如图,△ABC是⊙O的内接三角形.若OA∥CB,∠ACB=25°,则∠CAB= .
9.如图,AB,CD是⊙O的两条直径,E是BC的中点,连接BC,DE.若∠ABC=22°,则∠CDE的度数为( )
A.22° B.32° C.34° D.44°
10.如图,正六边形ABCDEF内接于⊙O,点 M在 上,则∠CME 的度数为( )
A.30° B.36° C. 45° D. 60°
11.(2023湖南)如图,AD是⊙O的直径,AB是⊙O的弦,BC与⊙O相切于点 B,连接OB,若∠ABC=65°,则∠BOD 的大小为 .
12.(2024北京)如图,⊙O的直径AB 平分弦CD(不是直径).若∠D=35°,则∠C= °.
第35 讲 圆中角度计算
典例精练
【例1】 (2024牡丹江)如图,四边形ABCD是⊙O的内接四边形,AB是⊙O的直径,若∠BEC=20°,则∠ADC的度数为( B)
A.100° B.110° C.120° D.130°
【例2】 如图,PM,PN分别与⊙O相切于A,B两点,C为⊙O上异于A,B的一点,连接AC,BC.若∠P=58°,则∠ACB 的大小是 61°或119° .
针对训练
1.(2024赤峰)如图,AD是⊙O的直径,AB 是⊙O的弦,半径OC⊥AB,连接CD,交OB 于点E,∠BOC=42°,则∠OED 的度数是(B )
A.61° B.63° C.65° D.67°
2.(2023黄冈)如图,在⊙O中,直径AB与弦CD 相交于点 P,连接AC,AD,BD,若∠C=20°,∠BPC=70°,则∠ADC=(D )
A.70° B.60° C.50° D.40°
3.如图,△ABC内接于⊙O,∠C=46°,连接OA,则∠OAB=(A )
A.44° B.45° C.54° D.67°
4.(2024泸州)如图,EA,ED 是⊙O的切线,切点为 A,D,点 B,C在⊙O上,若∠BAE+∠BCD=236°,则∠E=( C )
A.56° B.60° C.68° D.70°
5.如图是不倒翁的主视图,不倒翁的圆形脸恰好与帽子边沿 PA,PB分别相切于点A,B,不倒翁的鼻尖正好是圆心O,若∠OAB=28°,则∠APB 的度数为(C)
A.28° B.50° C.56° D.62°
6.(2023赤峰)如图,在圆内接四边形 ABCD中,∠BCD=105°,连接OB,OC,OD,BD,∠BOC=2∠COD,则∠CBD的度数是(A)
A.25° B.30° C.35° D.40°
7.(2023安徽)如图,正五边形ABCDE 内接于⊙O,连接OC,OD,则∠BAE-∠COD=(D)
A.60° B.54° C.48° D.36°
8.(2024山东)如图,△ABC是⊙O的内接三角形.若OA∥CB,∠ACB=25°,则∠CAB= 40°.
9.如图,AB,CD是⊙O的两条直径,E是BC的中点,连接BC,DE.若∠ABC=22°,则∠CDE的度数为(C)
A.22° B.32° C.34° D.44°
10.如图,正六边形ABCDEF 内接于⊙O,点 M在 上,则∠CME的度数为(D)
A.30° B.36° C. 45° D. 60°
11.(2023湖南)如图,AD是⊙O的直径,AB是⊙O的弦,BC与⊙O相切于点B,连接OB,若∠ABC=65°,则∠BOD 的大小为 50° .
12.(2024北京)如图,⊙O的直径AB平分弦CD(不是直径).若∠D=35°,则∠C= 55 °.
同课章节目录
