2025年中考数学复习--第39讲 内心和外心(含答案)
文档属性
| 名称 | 2025年中考数学复习--第39讲 内心和外心(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 237.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 00:00:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第39讲 内心和外心
典例精练
【例1】 已知O,I分别是△ABC的外心和内心,若 则∠BIC 的大小是 .
【例2】 (2022武汉)如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)判断△BDE 的形状,并证明你的结论;
(2)若 求 BC的长.
针对训练
1.如图,⊙O截△ABC的三条边所得的弦长相等,则下列说法正确的是( )
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
2.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )
A. h=R+r B. R=2r
3.(2023武昌)已知,在△ABC中,. 以AB为直径的圆经过△ABC的外心,则AB的长为
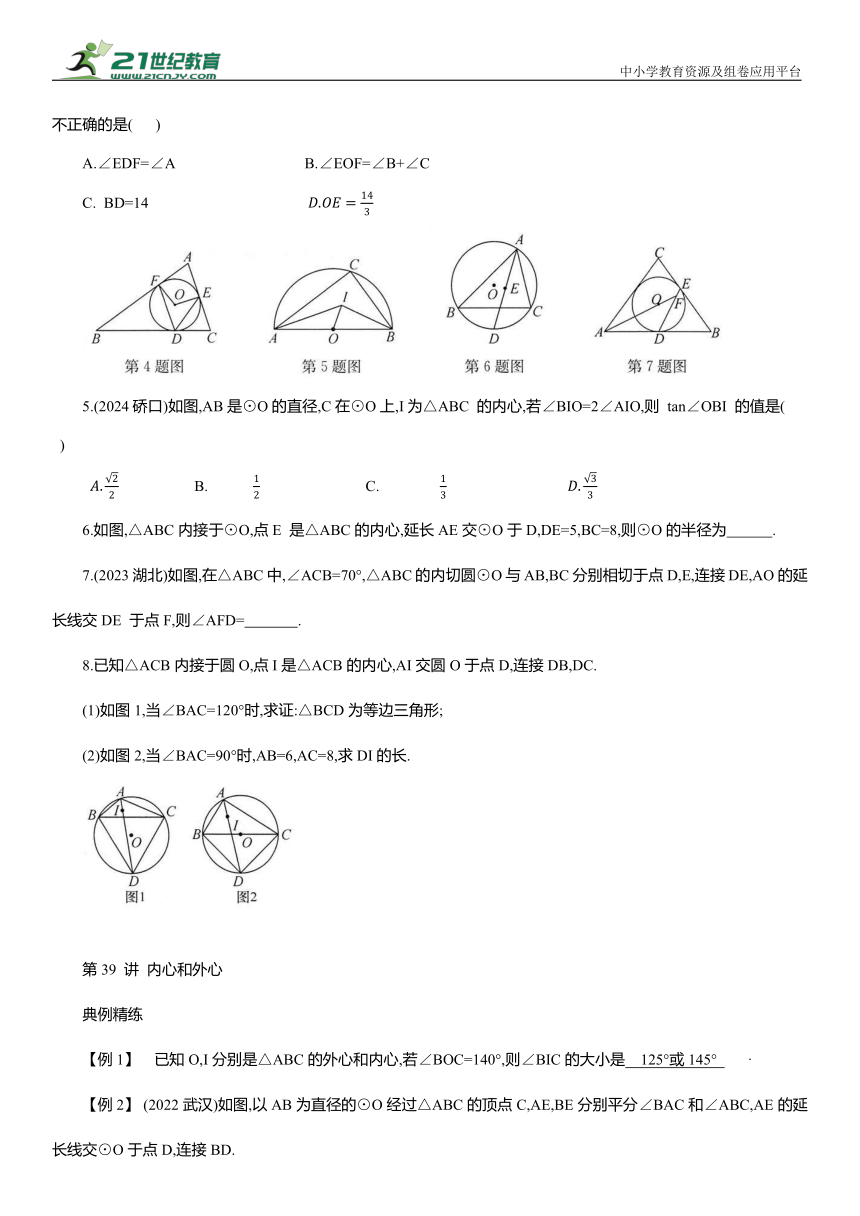
4.(2024江汉)如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=20,BC=21,CA=13,则下列说法不正确的是( )
A.∠EDF=∠A B.∠EOF=∠B+∠C
C. BD=14
5.(2024硚口)如图,AB是⊙O的直径,C在⊙O上,I为△ABC 的内心,若∠BIO=2∠AIO,则 tan∠OBI 的值是( )
B. C.
6.如图,△ABC内接于⊙O,点E 是△ABC的内心,延长AE交⊙O于D,DE=5,BC=8,则⊙O的半径为 .
7.(2023湖北)如图,在△ABC中,∠ACB=70°,△ABC的内切圆⊙O与AB,BC分别相切于点D,E,连接DE,AO的延长线交DE 于点F,则∠AFD= .
8.已知△ACB内接于圆O,点I是△ACB的内心,AI交圆O于点D,连接DB,DC.
(1)如图1,当∠BAC=120°时,求证:△BCD为等边三角形;
(2)如图2,当∠BAC=90°时,AB=6,AC=8,求DI的长.
第39 讲 内心和外心
典例精练
【例1】 已知O,I分别是△ABC的外心和内心,若∠BOC=140°,则∠BIC的大小是 125°或145° ·
【例2】 (2022武汉)如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)判断△BDE 的形状,并证明你的结论;
(2)若 求BC的长.
解:(1)△BDE为等腰直角三角形.
∵AE平分∠BAC,BE平分∠ABC,∴∠BAE=∠CAD=∠CBD,∠ABE=∠EBC.
∵∠BED=∠BAE+∠ABE,∠DBE=∠CBD+∠EBC,∴∠BED=∠DBE.∴BD=ED.
∵AB为直径,∴∠ADB=90°.∴△BDE 是等腰直角三角形.
(2)连接OC,CD,OD,设OD交BC于点F,则∠DBC=∠CAD=∠BAD=∠BCD,∴BD=DC.
∵OB=OC,∴OD垂直平分BC.∵△BDE是等腰直角三角形,
∵AB=10,∴OB=OD=5.设OF=t,则 解得t=3.
∴BF=4.∴BC=8.
针对训练
1.如图,⊙O截△ABC的三条边所得的弦长相等,则下列说法正确的是(A)
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
2.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是(C)
A. h=R+r B. R=2r
3.(2023武昌)已知,在△ABC中,AC=4,BC=3 ,以AB为直径的圆经过△ABC的外心,则AB的长为 或
4.(2024江汉)如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=20,BC=21,CA=13,则下列说法不正确的是(A)
A.∠EDF=∠A B.∠EOF=∠B+∠C
C. BD=14
5.(2024硚口)如图,AB是⊙O 的直径,C在⊙O上,I为△ABC 的内心,若∠BIO=2∠AIO,则tan∠OBI的值是(B)
B. C.
6.如图,△ABC内接于⊙O,点E 是△ABC的内心,延长AE交⊙O于D,DE=5,BC=8,则⊙O的半径为 .
7.(2023湖北)如图,在△ABC中,∠ACB=70°,△ABC的内切圆⊙O与AB,BC分别相切于点D,E,连接DE,AO的延长线交DE于点F,则∠AFD= 35° .
8.已知△ACB内接于圆O,点I是△ACB的内心,AI交圆O于点D,连接DB,DC.
(1)如图1,当∠BAC=120°时,求证:△BCD为等边三角形;
(2)如图2,当∠BAC=90°时,AB=6,AC=8,求DI的长.
解:(1)证明:∵点I是△ACB的内心,∠BAC=120°,
∴∠BAD=∠CAD=60°.
∴∠BCD=∠CBD=∠BDC=60°.
∴△BCD 为等边三角形.
(2)连接 BI,则∠ABI=∠CBI.
∵∠CBD=∠CAD =∠BAD=∠BCD,
∴BD=CD,∠ABI+∠BAD=∠CBI+∠CBD,即∠BID=∠DBI.
∴DI=BD.
∵∠BAC=90°,AB=6,AC=8,∴BC=10.
∵∠BDC=90°,∴BD=CD=5
第39讲 内心和外心
典例精练
【例1】 已知O,I分别是△ABC的外心和内心,若 则∠BIC 的大小是 .
【例2】 (2022武汉)如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)判断△BDE 的形状,并证明你的结论;
(2)若 求 BC的长.
针对训练
1.如图,⊙O截△ABC的三条边所得的弦长相等,则下列说法正确的是( )
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
2.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )
A. h=R+r B. R=2r
3.(2023武昌)已知,在△ABC中,. 以AB为直径的圆经过△ABC的外心,则AB的长为
4.(2024江汉)如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=20,BC=21,CA=13,则下列说法不正确的是( )
A.∠EDF=∠A B.∠EOF=∠B+∠C
C. BD=14
5.(2024硚口)如图,AB是⊙O的直径,C在⊙O上,I为△ABC 的内心,若∠BIO=2∠AIO,则 tan∠OBI 的值是( )
B. C.
6.如图,△ABC内接于⊙O,点E 是△ABC的内心,延长AE交⊙O于D,DE=5,BC=8,则⊙O的半径为 .
7.(2023湖北)如图,在△ABC中,∠ACB=70°,△ABC的内切圆⊙O与AB,BC分别相切于点D,E,连接DE,AO的延长线交DE 于点F,则∠AFD= .
8.已知△ACB内接于圆O,点I是△ACB的内心,AI交圆O于点D,连接DB,DC.
(1)如图1,当∠BAC=120°时,求证:△BCD为等边三角形;
(2)如图2,当∠BAC=90°时,AB=6,AC=8,求DI的长.
第39 讲 内心和外心
典例精练
【例1】 已知O,I分别是△ABC的外心和内心,若∠BOC=140°,则∠BIC的大小是 125°或145° ·
【例2】 (2022武汉)如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD.
(1)判断△BDE 的形状,并证明你的结论;
(2)若 求BC的长.
解:(1)△BDE为等腰直角三角形.
∵AE平分∠BAC,BE平分∠ABC,∴∠BAE=∠CAD=∠CBD,∠ABE=∠EBC.
∵∠BED=∠BAE+∠ABE,∠DBE=∠CBD+∠EBC,∴∠BED=∠DBE.∴BD=ED.
∵AB为直径,∴∠ADB=90°.∴△BDE 是等腰直角三角形.
(2)连接OC,CD,OD,设OD交BC于点F,则∠DBC=∠CAD=∠BAD=∠BCD,∴BD=DC.
∵OB=OC,∴OD垂直平分BC.∵△BDE是等腰直角三角形,
∵AB=10,∴OB=OD=5.设OF=t,则 解得t=3.
∴BF=4.∴BC=8.
针对训练
1.如图,⊙O截△ABC的三条边所得的弦长相等,则下列说法正确的是(A)
A.点O是△ABC的内心
B.点O是△ABC的外心
C.△ABC是正三角形
D.△ABC是等腰三角形
2.设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是(C)
A. h=R+r B. R=2r
3.(2023武昌)已知,在△ABC中,AC=4,BC=3 ,以AB为直径的圆经过△ABC的外心,则AB的长为 或
4.(2024江汉)如图,△ABC的内切圆⊙O与BC,CA,AB分别相切于点D,E,F,且AB=20,BC=21,CA=13,则下列说法不正确的是(A)
A.∠EDF=∠A B.∠EOF=∠B+∠C
C. BD=14
5.(2024硚口)如图,AB是⊙O 的直径,C在⊙O上,I为△ABC 的内心,若∠BIO=2∠AIO,则tan∠OBI的值是(B)
B. C.
6.如图,△ABC内接于⊙O,点E 是△ABC的内心,延长AE交⊙O于D,DE=5,BC=8,则⊙O的半径为 .
7.(2023湖北)如图,在△ABC中,∠ACB=70°,△ABC的内切圆⊙O与AB,BC分别相切于点D,E,连接DE,AO的延长线交DE于点F,则∠AFD= 35° .
8.已知△ACB内接于圆O,点I是△ACB的内心,AI交圆O于点D,连接DB,DC.
(1)如图1,当∠BAC=120°时,求证:△BCD为等边三角形;
(2)如图2,当∠BAC=90°时,AB=6,AC=8,求DI的长.
解:(1)证明:∵点I是△ACB的内心,∠BAC=120°,
∴∠BAD=∠CAD=60°.
∴∠BCD=∠CBD=∠BDC=60°.
∴△BCD 为等边三角形.
(2)连接 BI,则∠ABI=∠CBI.
∵∠CBD=∠CAD =∠BAD=∠BCD,
∴BD=CD,∠ABI+∠BAD=∠CBI+∠CBD,即∠BID=∠DBI.
∴DI=BD.
∵∠BAC=90°,AB=6,AC=8,∴BC=10.
∵∠BDC=90°,∴BD=CD=5
同课章节目录
