2025年中考数学复习--中档题训练(五)(含答案)
文档属性
| 名称 | 2025年中考数学复习--中档题训练(五)(含答案) | 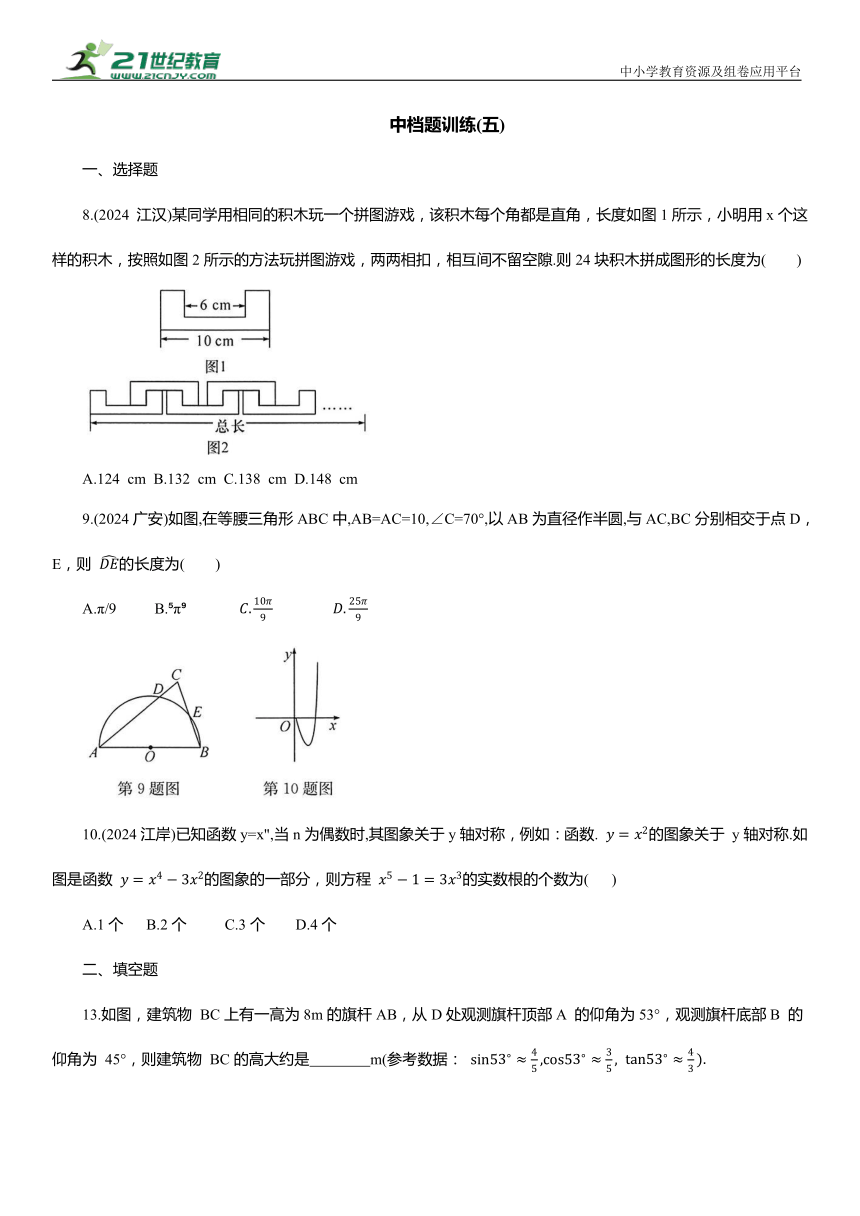 | |
| 格式 | docx | ||
| 文件大小 | 280.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 20:49:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
中档题训练(五)
一、选择题
8.(2024 江汉)某同学用相同的积木玩一个拼图游戏,该积木每个角都是直角,长度如图1所示,小明用x个这样的积木,按照如图2所示的方法玩拼图游戏,两两相扣,相互间不留空隙.则24块积木拼成图形的长度为( )
A.124 cm B.132 cm C.138 cm D.148 cm
9.(2024广安)如图,在等腰三角形ABC中,AB=AC=10,∠C=70°,以AB为直径作半圆,与AC,BC分别相交于点D,E,则 的长度为( )
A.π/9 B. π
10.(2024江岸)已知函数y=x",当n为偶数时,其图象关于y轴对称,例如:函数. 的图象关于 y轴对称.如图是函数 的图象的一部分,则方程 的实数根的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,建筑物 BC上有一高为8m的旗杆AB,从D处观测旗杆顶部A 的仰角为53°,观测旗杆底部B 的仰角为 45°,则建筑物 BC的高大约是 m(参考数据:
14.(2024 山东)如图,已知∠MAN,以点 A 为圆心,以适当长为半径作弧,分别与 AM,AN 相交于点B,C;分别以B,C为圆心,以大于 BC的长为半径作弧,两弧在∠MAN 内部相交于点 P,作射线AP.分别以A,B为圆心,以大于 AB的长为半径作弧,两弧相交于点 D,E,作直线DE分别与AB,AP 相交于点 F,Q.若AB=4,∠PQE=67.5°,则F到AN 的距离为 .
15.(2024江岸)如图,在△ABC中,点 D,E分别在AB,AC上,DE∥BC.若 且 CE=4,则线段AE的长是 .
三、解答题
21.(2024 青山)如图是由小正方形组成的8×6的网格,每个小正方形的顶点叫作格点,点A,B在格点上,点C在水平网格上,仅用无刻度的直尺在给定的网格中完成画图,每个画图的画线不得超过三条.
(1)如图1,点P 是AB 与网格线的交点,先画点P 绕点A 逆时针旋转90°的对应点 Q,再在AB上画点H,使得△QCH 的周长最小;
(2)如图2,点 P是AB 上一点,先将线段 BC沿BA 方向平移得线段AD(点 B 与点 A 对应,点C与点D 对应),再在线段AP上画点E,使得2AE=EP.
22.(2024贵州)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(单位:盒)与销售单价x(单位:元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 56 52 48 44 40
(1)求y与x的函数解析式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
23.(2024硚口)问题情境 CD 是等边△ABC的中线,点P 在线段CD 上运动(不包括端点 C,D),将线段 PA 绕点 P 顺时针旋转,点A 的对应点E 落在射线 BC 上,探究∠APE 的大小.记∠CAP=α.
问题探究 (1)如图1,将问题特殊化,当α=30°时,直接写出∠APE的大小;
(2)如图2,将问题一般化,当( 时,求证: 是定值.
24.如图,抛物线 交x轴于A,B两点,交y轴于点C(0,-2),其对称轴为直线
(1)直接写出抛物线C 的解析式和点 A,B的坐标;
(2)点 D 在第一象限的抛物线上,若 tan∠BCD 求点 D的坐标.
中档题训练(五)
一、选择题
8.(2024 江汉)某同学用相同的积木玩一个拼图游戏,该积木每个角都是直角,长度如图1所示,小明用x个这样的积木,按照如图2所示的方法玩拼图游戏,两两相扣,相互间不留空隙.则24块积木拼成图形的长度为(D)
A.124 cm B.132 cm C.138 cm D.148 cm
9.(2024 广安)如图,在等腰三角形ABC中,AB=AC=10,∠C=70°,以AB为直径作半圆,与AC,BC分别相交于点 D,E,则DE的长度为(C)
A.π/9 B. π/
10.(2024 江岸)已知函数y=x",当n为偶数时,其图象关于y轴对称,例如:函数. 的图象关于y轴对称.如图是函数 的图象的一部分,则方程 的实数根的个数为(C)
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,建筑物 BC上有一高为8m的旗杆AB,从D处观测旗杆顶部A 的仰角为53°,观测旗杆底部B 的仰角为 45°,则建筑物 BC 的高大约是 24 m(参考数据:
14.(2024 山东)如图,已知∠MAN,以点 A 为圆心,以适当长为半径作弧,分别与AM,AN 相交于点B,C;分别以 B,C为圆心,以大于 BC的长为半径作弧,两弧在∠MAN 内部相交于点 P,作射线 AP.分别以A,B为圆心,以大于 AB的长为半径作弧,两弧相交于点 D,E,作直线DE分别与AB,AP 相交于点 F,Q.若AB=4,∠PQE=67.5°,则 F到AN 的距离为 .
15.(2024江岸)如图,在△ABC中,点 D,E分别在AB,AC上,DE∥BC.若S△ADE=S△BCE,.且CE=4,则线段 AE 的长是
三、解答题
21.(2024 青山)如图是由小正方形组成的8×6的网格,每个小正方形的顶点叫作格点,点A,B在格点上,点C在水平网格上,仅用无刻度的直尺在给定的网格中完成画图,每个画图的画线不得超过三条.
(1)如图1,点P 是AB 与网格线的交点,先画点P 绕点A 逆时针旋转90°的对应点 Q,再在AB上画点H,使得△QCH的周长最小;
(2)如图2,点 P是AB 上一点,先将线段 BC 沿BA 方向平移得线段AD(点 B 与点 A 对应,点C与点D 对应),再在线段AP上画点E,使得2AE=EP.
22.(2024贵州)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(单位:盒)与销售单价x(单位:元)是一次函数关系,下表是 y与x 的几组对应值.
销售单价x/元 …… 12 14 16 18 20 ……
销售量y/盒 ·· 56 52 48 44 40 …
(1)求y与x的函数解析式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
解:(1)设y与x的函数解析式为y=k. c+b,把 x = 12. y = 56;x = 20. y=40 代入.得 解得
∴y与: 的函数解析式为y - 2x+80.
(2)设日销售利润为ω元,根据题意,得 (x-10)·y= (x-10)(-2x+80)-…2x +
∴当x=25时.ω有最大值为450.
∴糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元.
(3)设日销售利润为 ω元.根据题意:得ω=(x-10-m) ·y=(x-10-m)(-2x+80)
∴当 时,ω有最大值为
∵糖果日销售获得的最大利润为392元,
80m=392,
化简得
解得
当m=58时,
则每盒的利润为54-10-58---14<0,舍去,∴m的值为2.
23.(2024硚口)问题情境 CD 是等边△ABC的中线,点P 在线段CD上运动(不包括端点 C,D),将线段 PA 绕点 P 顺时针旋转,点A 的对应点E 落在射线 BC 上,探究∠APE 的大小.记∠CAP=-α.
问题探究 (1)如图1,将问题特殊化,当α=30°时,直接写出∠APE的大小;
(2)如图2,将问题一般化,当( 时,求证: 是定值.
解:(1)120°.
(2)连接BP,在AC上取点F,使得 AF=EC,过点 P作PG⊥AC于G.因为CD是等边△ABC的中线,所以CD是AB 的垂直平分线、
∴PB=PA,∠PAB=∠PBA..
∴∠PBC=60°-∠PBA ==60°……∠PAB -∠PAC.
∵PE=PA,∴PE=PB.∴∠PEC=三PBC.
∴∠PAC--∠PEC.
在△PAF和△PEC中
∴APAF≌△PEC.
∴PF=FC.又PG⊥CF.∴FG=--CG.
在 Rt, PCG中.
∴CF=FG=()= CP.
24.如图,抛物线 交x轴于A,B两点,交y轴于点C(0,-2),其对称轴为直线
(1)直接写出抛物线C 的解析式和点 A,B的坐标;
(2)点D 在第一象限的抛物线上,若 tan∠BCD 求点D的坐标.
解: A(-1,0),B(4.0).
(2)∵OB=4,OC==2,
在 Rt△BOC中. tan∠CBO=
∴∠BCD=∠CBO.设CD交x轴于E(a,0).
∴EC=EB=4-a,
在Rt△COE 中, 解得
于是可求CE的解析式为
联立.
解得 舍去)
中档题训练(五)
一、选择题
8.(2024 江汉)某同学用相同的积木玩一个拼图游戏,该积木每个角都是直角,长度如图1所示,小明用x个这样的积木,按照如图2所示的方法玩拼图游戏,两两相扣,相互间不留空隙.则24块积木拼成图形的长度为( )
A.124 cm B.132 cm C.138 cm D.148 cm
9.(2024广安)如图,在等腰三角形ABC中,AB=AC=10,∠C=70°,以AB为直径作半圆,与AC,BC分别相交于点D,E,则 的长度为( )
A.π/9 B. π
10.(2024江岸)已知函数y=x",当n为偶数时,其图象关于y轴对称,例如:函数. 的图象关于 y轴对称.如图是函数 的图象的一部分,则方程 的实数根的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,建筑物 BC上有一高为8m的旗杆AB,从D处观测旗杆顶部A 的仰角为53°,观测旗杆底部B 的仰角为 45°,则建筑物 BC的高大约是 m(参考数据:
14.(2024 山东)如图,已知∠MAN,以点 A 为圆心,以适当长为半径作弧,分别与 AM,AN 相交于点B,C;分别以B,C为圆心,以大于 BC的长为半径作弧,两弧在∠MAN 内部相交于点 P,作射线AP.分别以A,B为圆心,以大于 AB的长为半径作弧,两弧相交于点 D,E,作直线DE分别与AB,AP 相交于点 F,Q.若AB=4,∠PQE=67.5°,则F到AN 的距离为 .
15.(2024江岸)如图,在△ABC中,点 D,E分别在AB,AC上,DE∥BC.若 且 CE=4,则线段AE的长是 .
三、解答题
21.(2024 青山)如图是由小正方形组成的8×6的网格,每个小正方形的顶点叫作格点,点A,B在格点上,点C在水平网格上,仅用无刻度的直尺在给定的网格中完成画图,每个画图的画线不得超过三条.
(1)如图1,点P 是AB 与网格线的交点,先画点P 绕点A 逆时针旋转90°的对应点 Q,再在AB上画点H,使得△QCH 的周长最小;
(2)如图2,点 P是AB 上一点,先将线段 BC沿BA 方向平移得线段AD(点 B 与点 A 对应,点C与点D 对应),再在线段AP上画点E,使得2AE=EP.
22.(2024贵州)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(单位:盒)与销售单价x(单位:元)是一次函数关系,下表是y与x的几组对应值.
销售单价x/元 … 12 14 16 18 20 …
销售量y/盒 56 52 48 44 40
(1)求y与x的函数解析式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
23.(2024硚口)问题情境 CD 是等边△ABC的中线,点P 在线段CD 上运动(不包括端点 C,D),将线段 PA 绕点 P 顺时针旋转,点A 的对应点E 落在射线 BC 上,探究∠APE 的大小.记∠CAP=α.
问题探究 (1)如图1,将问题特殊化,当α=30°时,直接写出∠APE的大小;
(2)如图2,将问题一般化,当( 时,求证: 是定值.
24.如图,抛物线 交x轴于A,B两点,交y轴于点C(0,-2),其对称轴为直线
(1)直接写出抛物线C 的解析式和点 A,B的坐标;
(2)点 D 在第一象限的抛物线上,若 tan∠BCD 求点 D的坐标.
中档题训练(五)
一、选择题
8.(2024 江汉)某同学用相同的积木玩一个拼图游戏,该积木每个角都是直角,长度如图1所示,小明用x个这样的积木,按照如图2所示的方法玩拼图游戏,两两相扣,相互间不留空隙.则24块积木拼成图形的长度为(D)
A.124 cm B.132 cm C.138 cm D.148 cm
9.(2024 广安)如图,在等腰三角形ABC中,AB=AC=10,∠C=70°,以AB为直径作半圆,与AC,BC分别相交于点 D,E,则DE的长度为(C)
A.π/9 B. π/
10.(2024 江岸)已知函数y=x",当n为偶数时,其图象关于y轴对称,例如:函数. 的图象关于y轴对称.如图是函数 的图象的一部分,则方程 的实数根的个数为(C)
A.1个 B.2个 C.3个 D.4个
二、填空题
13.如图,建筑物 BC上有一高为8m的旗杆AB,从D处观测旗杆顶部A 的仰角为53°,观测旗杆底部B 的仰角为 45°,则建筑物 BC 的高大约是 24 m(参考数据:
14.(2024 山东)如图,已知∠MAN,以点 A 为圆心,以适当长为半径作弧,分别与AM,AN 相交于点B,C;分别以 B,C为圆心,以大于 BC的长为半径作弧,两弧在∠MAN 内部相交于点 P,作射线 AP.分别以A,B为圆心,以大于 AB的长为半径作弧,两弧相交于点 D,E,作直线DE分别与AB,AP 相交于点 F,Q.若AB=4,∠PQE=67.5°,则 F到AN 的距离为 .
15.(2024江岸)如图,在△ABC中,点 D,E分别在AB,AC上,DE∥BC.若S△ADE=S△BCE,.且CE=4,则线段 AE 的长是
三、解答题
21.(2024 青山)如图是由小正方形组成的8×6的网格,每个小正方形的顶点叫作格点,点A,B在格点上,点C在水平网格上,仅用无刻度的直尺在给定的网格中完成画图,每个画图的画线不得超过三条.
(1)如图1,点P 是AB 与网格线的交点,先画点P 绕点A 逆时针旋转90°的对应点 Q,再在AB上画点H,使得△QCH的周长最小;
(2)如图2,点 P是AB 上一点,先将线段 BC 沿BA 方向平移得线段AD(点 B 与点 A 对应,点C与点D 对应),再在线段AP上画点E,使得2AE=EP.
22.(2024贵州)某超市购入一批进价为10元/盒的糖果进行销售,经市场调查发现:销售单价不低于进价时,日销售量y(单位:盒)与销售单价x(单位:元)是一次函数关系,下表是 y与x 的几组对应值.
销售单价x/元 …… 12 14 16 18 20 ……
销售量y/盒 ·· 56 52 48 44 40 …
(1)求y与x的函数解析式;
(2)糖果销售单价定为多少元时,所获日销售利润最大,最大利润是多少
(3)若超市决定每销售一盒糖果向儿童福利院赠送一件价值为m元的礼品,赠送礼品后,为确保该种糖果日销售获得的最大利润为392元,求m的值.
解:(1)设y与x的函数解析式为y=k. c+b,把 x = 12. y = 56;x = 20. y=40 代入.得 解得
∴y与: 的函数解析式为y - 2x+80.
(2)设日销售利润为ω元,根据题意,得 (x-10)·y= (x-10)(-2x+80)-…2x +
∴当x=25时.ω有最大值为450.
∴糖果销售单价定为25元时,所获日销售利润最大,最大利润是450元.
(3)设日销售利润为 ω元.根据题意:得ω=(x-10-m) ·y=(x-10-m)(-2x+80)
∴当 时,ω有最大值为
∵糖果日销售获得的最大利润为392元,
80m=392,
化简得
解得
当m=58时,
则每盒的利润为54-10-58---14<0,舍去,∴m的值为2.
23.(2024硚口)问题情境 CD 是等边△ABC的中线,点P 在线段CD上运动(不包括端点 C,D),将线段 PA 绕点 P 顺时针旋转,点A 的对应点E 落在射线 BC 上,探究∠APE 的大小.记∠CAP=-α.
问题探究 (1)如图1,将问题特殊化,当α=30°时,直接写出∠APE的大小;
(2)如图2,将问题一般化,当( 时,求证: 是定值.
解:(1)120°.
(2)连接BP,在AC上取点F,使得 AF=EC,过点 P作PG⊥AC于G.因为CD是等边△ABC的中线,所以CD是AB 的垂直平分线、
∴PB=PA,∠PAB=∠PBA..
∴∠PBC=60°-∠PBA ==60°……∠PAB -∠PAC.
∵PE=PA,∴PE=PB.∴∠PEC=三PBC.
∴∠PAC--∠PEC.
在△PAF和△PEC中
∴APAF≌△PEC.
∴PF=FC.又PG⊥CF.∴FG=--CG.
在 Rt, PCG中.
∴CF=FG=()= CP.
24.如图,抛物线 交x轴于A,B两点,交y轴于点C(0,-2),其对称轴为直线
(1)直接写出抛物线C 的解析式和点 A,B的坐标;
(2)点D 在第一象限的抛物线上,若 tan∠BCD 求点D的坐标.
解: A(-1,0),B(4.0).
(2)∵OB=4,OC==2,
在 Rt△BOC中. tan∠CBO=
∴∠BCD=∠CBO.设CD交x轴于E(a,0).
∴EC=EB=4-a,
在Rt△COE 中, 解得
于是可求CE的解析式为
联立.
解得 舍去)
同课章节目录
