2025年中考数学复习--第5 讲 阅读理解与规律探索(含答案)
文档属性
| 名称 | 2025年中考数学复习--第5 讲 阅读理解与规律探索(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 234.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 20:54:09 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第5 讲 阅读理解与规律探索
典例精练
【例1】 观察等式:2 ··.已知按一定规律排列的一组数:2 ,2 ,2 ,……,2 ,2 .若: 用含a的式子表示这组数的和是( )
【例2】 (2024山东)已知一列均不为1的数a ,a ,a ,…, an满足如下关系: 若 则a 的值是( )
B. C. -3 D.2
针对训练
1.按一定规律排列的单项式:a,-2a,4a,-8a,16a,-32a,…,第n个单项式是( )
B.(-2)"a D.2"a
2.按照一定规律排列的n个数:-2,4,-8,16,-32,64,….若最后的三个数的和为768,则n为( )
A.9 B.10 C.11 D.12
3.将正整数1~2018按一定规律排列(如图),平移图中带阴影的方框,方框中三个数的和可能是( )
A.2 019 B.2 018 C.2 016 D.2 013
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
第3题图
4.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图1就是一个幻方.图2是一个未完成的幻方,其中x与y的和是( )
A.9 B.10 C.11 D.12
5.勾股定理最早出现在商高的《周髀算经》中:“勾广三,股修四,径隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…….这类勾股数的特点是:勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数、弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;….若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含 m的式子表示).
6.人们把 这个数叫作黄金比,著名数学家华罗庚的优选法中的“0.618法”就应用了黄金比.设 记 则
7.观察下列算式:a +1=19,….它们有一定的规律性,把第n个算式的结果记为 an,则 的值是( )
A.
8.如图,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数字之和,例如第4行的6为第3行中两个3的和.若在“杨辉三角”中从第2行左边的1开始按“锯齿形”排列的箭头所指的数依次构成一个数列:( 10,a =5,…,则a +a 白的值为( )
A.1275 B.1 326 C.1 378 D.1 431
9.如图,三个图形都是边长为1的小正方形组成的网格.第一个图形有1×1个小正方形,所有线段的和为4;第二个图形有2×2个小正方形,所有线段的和为12;第三个图形有3×3个小正方形,所有线段的和为24.按此规律,则第n个图形中所有线段的和为 (用含n的代数式表示).
10.如图,从左至右,第1个图形由1个正六边形、6个正方形和6个等边三角形组成;第2个图形由2个正六边形、11个正方形和10个等边三角形组成;第3个图形由3个正六边形、16个正方形和14个等边三角形组成;……按照此规律,第22个图形中正方形和等边三角形的个数之和为 .
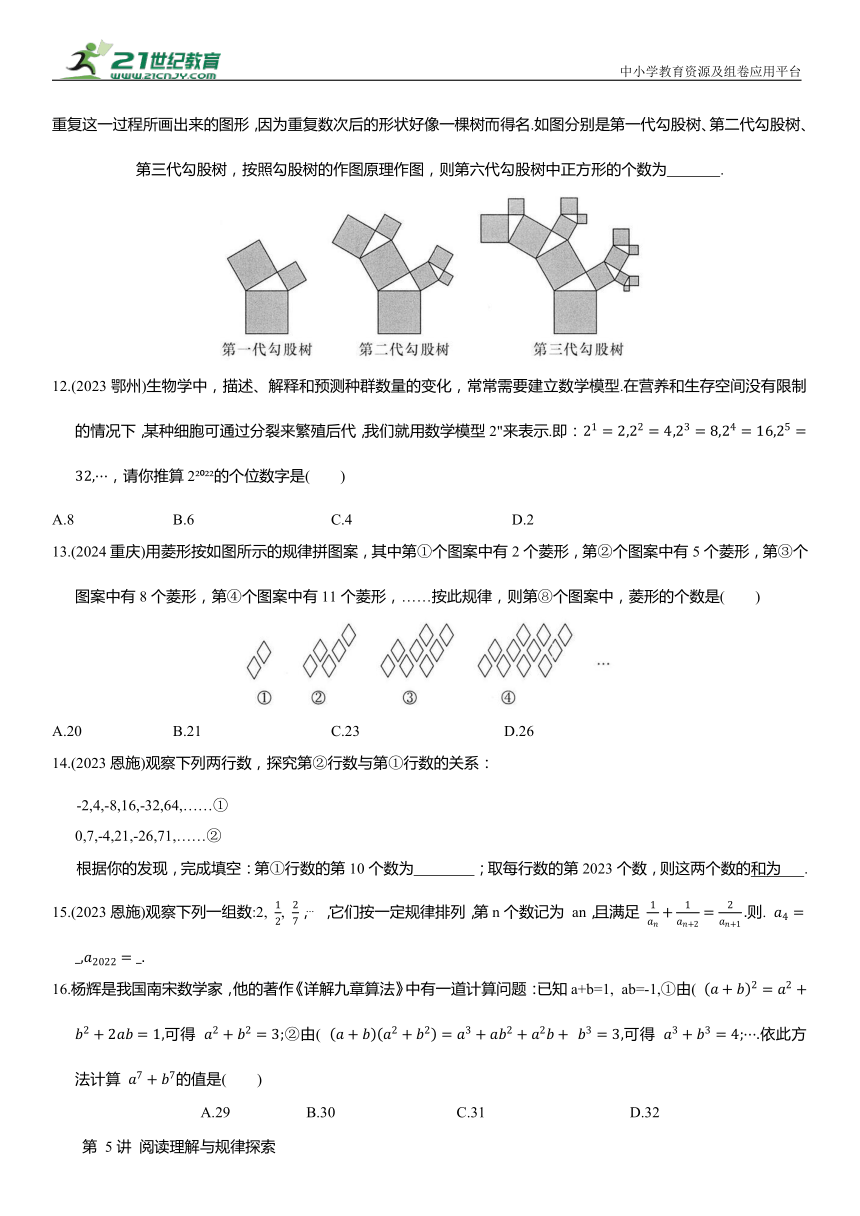
勾股树是以正方形的一条边为斜边向外作直角三角形,再分别以该直角三角形的两条直角边为边向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好像一棵树而得名.如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 .
12.(2023鄂州)生物学中,描述、解释和预测种群数量的变化,常常需要建立数学模型.在营养和生存空间没有限制的情况下,某种细胞可通过分裂来繁殖后代,我们就用数学模型2"来表示.即: ,请你推算2 的个位数字是( )
A.8 B.6 C.4 D.2
13.(2024重庆)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,……按此规律,则第⑧个图案中,菱形的个数是( )
A.20 B.21 C.23 D.26
14.(2023恩施)观察下列两行数,探究第②行数与第①行数的关系:
-2,4,-8,16,-32,64,……①
0,7,-4,21,-26,71,……②
根据你的发现,完成填空:第①行数的第10个数为 ;取每行数的第2023个数,则这两个数的和为 .
15.(2023恩施)观察下列一组数:2, , , ,它们按一定规律排列,第n个数记为 an,且满足 则.
16.杨辉是我国南宋数学家,他的著作《详解九章算法》中有一道计算问题:已知a+b=1, ab=-1,①由( 可得 ②由( 可得 依此方法计算 的值是( )
A.29 B.30 C.31 D.32
第 5讲 阅读理解与规律探索
典例精练
【例1】 观察等式:2 ·.已知按一定规律排列的一组数:2 ,2 ,2 ,……,2 ,2 .若 用含a的式子表示这组数的和是(C)
【例2】 (2024山东)已知一列均不为1的数(a ,a ,a ,…, an满足如下关系: 若 则a 023的值是(A)
B. C.-3 D.2
针对训练
1.按一定规律排列的单项式:a,-2a,4a,-8a,16a,-32a,…,第n个单项式是( A)
B.(-2)"a D.2"a
2.按照一定规律排列的n个数:-2,4,-8,16,-32,64,….若最后的三个数的和为768,则n为(B)
A.9 B.10 C.11 D.12
3.将正整数1~2018按一定规律排列(如图),平移图中带阴影的方框,方框中三个数的和可能是(D)
A.2 019 B.2 018 C.2 016 D.2 013
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
第3题图
4.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图1就是一个幻方.图2是一个未完成的幻方,其中x与y的和是(D)
A.9 B.10 C.11 D.12
勾股定理最早出现在商高的《周髀算经》中:“勾广三,股修四,径隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…….这类勾股数的特点是:勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数、弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;….若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含m的式子表示).
6.人们把 这个数叫作黄金比,著名数学家华罗庚的优选法中的“0.618法”就应用了黄金比.设 记 则
7.观察下列算式:a +1=19,…….它们有一定的规律性,把第n个算式的结果记为 an,则 的值是(C)
A.
8.如图,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数字之和,例如第4行的6为第3行中两个3的和.若在“杨辉三角”中从第2行左边的1开始按“锯齿形”排列的箭头所指的数依次构成一个数列: 10,a =5,…,则 的值为(B)
A.1 275 B.1326 C.1 378 D.1431
9.如图,三个图形都是边长为1的小正方形组成的网格.第一个图形有1×1个小正方形,所有线段的和为4;第二个图形有2×2个小正方形,所有线段的和为12;第三个图形有3×3个小正方形,所有线段的和为24.按此规律,则第n个图形中所有线段的和为 2n(n+1) (用含n的代数式表示).
10.如图,从左至右,第1个图形由1个正六边形、6个正方形和6个等边三角形组成;第2个图形由2个正六边形、11个正方形和10个等边三角形组成;第3个图形由3个正六边形、16个正方形和14个等边三角形组成;……按照此规律,第22个图形中正方形和等边三角形的个数之和为 201 .
11.勾股树是以正方形的一条边为斜边向外作直角三角形,再分别以该直角三角形的两条直角边为边向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好像一棵树而得名.如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 127 .
12.(2023 鄂州)生物学中,描述、解释和预测种群数量的变化,常常需要建立数学模型.在营养和生存空间没有限制的情况下,某种细胞可通过分裂来繁殖后代,我们就用数学模型2"来表示.即:2 请你推算2 的个位数字是(C )
A.8 B.6 C.4 D.2
13.(2024重庆)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,……按此规律,则第⑧个图案中,菱形的个数是(C)
A.20 B.21 C.23 D.26
14.(2023恩施)观察下列两行数,探究第②行数与第①行数的关系:
-2,4,-8,16,-32,64,……①
0,7,-4,21,-26,71,……②
根据你的发现,完成填空:第①行数的第10个数为 1024 ;取每行数的第2023个数,则这两个数的和为 则
16.杨辉是我国南宋数学家,他的著作《详解九章算法》中有一道计算问题:已知a+b=1, ab=--1,①由( 可得 ②由( 可得 依此方法计算( 的值是(A)
A.29 B.30 C.31 D.32
第5 讲 阅读理解与规律探索
典例精练
【例1】 观察等式:2 ··.已知按一定规律排列的一组数:2 ,2 ,2 ,……,2 ,2 .若: 用含a的式子表示这组数的和是( )
【例2】 (2024山东)已知一列均不为1的数a ,a ,a ,…, an满足如下关系: 若 则a 的值是( )
B. C. -3 D.2
针对训练
1.按一定规律排列的单项式:a,-2a,4a,-8a,16a,-32a,…,第n个单项式是( )
B.(-2)"a D.2"a
2.按照一定规律排列的n个数:-2,4,-8,16,-32,64,….若最后的三个数的和为768,则n为( )
A.9 B.10 C.11 D.12
3.将正整数1~2018按一定规律排列(如图),平移图中带阴影的方框,方框中三个数的和可能是( )
A.2 019 B.2 018 C.2 016 D.2 013
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
第3题图
4.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图1就是一个幻方.图2是一个未完成的幻方,其中x与y的和是( )
A.9 B.10 C.11 D.12
5.勾股定理最早出现在商高的《周髀算经》中:“勾广三,股修四,径隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…….这类勾股数的特点是:勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数、弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;….若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含 m的式子表示).
6.人们把 这个数叫作黄金比,著名数学家华罗庚的优选法中的“0.618法”就应用了黄金比.设 记 则
7.观察下列算式:a +1=19,….它们有一定的规律性,把第n个算式的结果记为 an,则 的值是( )
A.
8.如图,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数字之和,例如第4行的6为第3行中两个3的和.若在“杨辉三角”中从第2行左边的1开始按“锯齿形”排列的箭头所指的数依次构成一个数列:( 10,a =5,…,则a +a 白的值为( )
A.1275 B.1 326 C.1 378 D.1 431
9.如图,三个图形都是边长为1的小正方形组成的网格.第一个图形有1×1个小正方形,所有线段的和为4;第二个图形有2×2个小正方形,所有线段的和为12;第三个图形有3×3个小正方形,所有线段的和为24.按此规律,则第n个图形中所有线段的和为 (用含n的代数式表示).
10.如图,从左至右,第1个图形由1个正六边形、6个正方形和6个等边三角形组成;第2个图形由2个正六边形、11个正方形和10个等边三角形组成;第3个图形由3个正六边形、16个正方形和14个等边三角形组成;……按照此规律,第22个图形中正方形和等边三角形的个数之和为 .
勾股树是以正方形的一条边为斜边向外作直角三角形,再分别以该直角三角形的两条直角边为边向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好像一棵树而得名.如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 .
12.(2023鄂州)生物学中,描述、解释和预测种群数量的变化,常常需要建立数学模型.在营养和生存空间没有限制的情况下,某种细胞可通过分裂来繁殖后代,我们就用数学模型2"来表示.即: ,请你推算2 的个位数字是( )
A.8 B.6 C.4 D.2
13.(2024重庆)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,……按此规律,则第⑧个图案中,菱形的个数是( )
A.20 B.21 C.23 D.26
14.(2023恩施)观察下列两行数,探究第②行数与第①行数的关系:
-2,4,-8,16,-32,64,……①
0,7,-4,21,-26,71,……②
根据你的发现,完成填空:第①行数的第10个数为 ;取每行数的第2023个数,则这两个数的和为 .
15.(2023恩施)观察下列一组数:2, , , ,它们按一定规律排列,第n个数记为 an,且满足 则.
16.杨辉是我国南宋数学家,他的著作《详解九章算法》中有一道计算问题:已知a+b=1, ab=-1,①由( 可得 ②由( 可得 依此方法计算 的值是( )
A.29 B.30 C.31 D.32
第 5讲 阅读理解与规律探索
典例精练
【例1】 观察等式:2 ·.已知按一定规律排列的一组数:2 ,2 ,2 ,……,2 ,2 .若 用含a的式子表示这组数的和是(C)
【例2】 (2024山东)已知一列均不为1的数(a ,a ,a ,…, an满足如下关系: 若 则a 023的值是(A)
B. C.-3 D.2
针对训练
1.按一定规律排列的单项式:a,-2a,4a,-8a,16a,-32a,…,第n个单项式是( A)
B.(-2)"a D.2"a
2.按照一定规律排列的n个数:-2,4,-8,16,-32,64,….若最后的三个数的和为768,则n为(B)
A.9 B.10 C.11 D.12
3.将正整数1~2018按一定规律排列(如图),平移图中带阴影的方框,方框中三个数的和可能是(D)
A.2 019 B.2 018 C.2 016 D.2 013
1 2 3 4 5 6 7 8
9 10 11 12 13 14 15 16
17 18 19 20 21 22 23 24
25 26 27 28 29 30 31 32
第3题图
4.幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等,例如图1就是一个幻方.图2是一个未完成的幻方,其中x与y的和是(D)
A.9 B.10 C.11 D.12
勾股定理最早出现在商高的《周髀算经》中:“勾广三,股修四,径隅五”.观察下列勾股数:3,4,5;5,12,13;7,24,25;…….这类勾股数的特点是:勾为奇数,弦与股相差为1.柏拉图研究了勾为偶数、弦与股相差为2的一类勾股数,如:6,8,10;8,15,17;….若此类勾股数的勾为2m(m≥3,m为正整数),则其弦是 (结果用含m的式子表示).
6.人们把 这个数叫作黄金比,著名数学家华罗庚的优选法中的“0.618法”就应用了黄金比.设 记 则
7.观察下列算式:a +1=19,…….它们有一定的规律性,把第n个算式的结果记为 an,则 的值是(C)
A.
8.如图,在“杨辉三角”中,除每行两边的数都是1外,其余每个数都是其“肩上”的两个数字之和,例如第4行的6为第3行中两个3的和.若在“杨辉三角”中从第2行左边的1开始按“锯齿形”排列的箭头所指的数依次构成一个数列: 10,a =5,…,则 的值为(B)
A.1 275 B.1326 C.1 378 D.1431
9.如图,三个图形都是边长为1的小正方形组成的网格.第一个图形有1×1个小正方形,所有线段的和为4;第二个图形有2×2个小正方形,所有线段的和为12;第三个图形有3×3个小正方形,所有线段的和为24.按此规律,则第n个图形中所有线段的和为 2n(n+1) (用含n的代数式表示).
10.如图,从左至右,第1个图形由1个正六边形、6个正方形和6个等边三角形组成;第2个图形由2个正六边形、11个正方形和10个等边三角形组成;第3个图形由3个正六边形、16个正方形和14个等边三角形组成;……按照此规律,第22个图形中正方形和等边三角形的个数之和为 201 .
11.勾股树是以正方形的一条边为斜边向外作直角三角形,再分别以该直角三角形的两条直角边为边向外作正方形,重复这一过程所画出来的图形,因为重复数次后的形状好像一棵树而得名.如图分别是第一代勾股树、第二代勾股树、第三代勾股树,按照勾股树的作图原理作图,则第六代勾股树中正方形的个数为 127 .
12.(2023 鄂州)生物学中,描述、解释和预测种群数量的变化,常常需要建立数学模型.在营养和生存空间没有限制的情况下,某种细胞可通过分裂来繁殖后代,我们就用数学模型2"来表示.即:2 请你推算2 的个位数字是(C )
A.8 B.6 C.4 D.2
13.(2024重庆)用菱形按如图所示的规律拼图案,其中第①个图案中有2个菱形,第②个图案中有5个菱形,第③个图案中有8个菱形,第④个图案中有11个菱形,……按此规律,则第⑧个图案中,菱形的个数是(C)
A.20 B.21 C.23 D.26
14.(2023恩施)观察下列两行数,探究第②行数与第①行数的关系:
-2,4,-8,16,-32,64,……①
0,7,-4,21,-26,71,……②
根据你的发现,完成填空:第①行数的第10个数为 1024 ;取每行数的第2023个数,则这两个数的和为 则
16.杨辉是我国南宋数学家,他的著作《详解九章算法》中有一道计算问题:已知a+b=1, ab=--1,①由( 可得 ②由( 可得 依此方法计算( 的值是(A)
A.29 B.30 C.31 D.32
同课章节目录
