2025年浙江省中考数学一轮复习专题检测 专题21 多边形与平行四边形(含解析)
文档属性
| 名称 | 2025年浙江省中考数学一轮复习专题检测 专题21 多边形与平行四边形(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 21:04:39 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专题21 多边形与平行四边形
一.选择题
1.(2025 济南模拟)已知一个多边形的内角和等于外角和,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
2.(2024 锦江区校级模拟)在 ABCD中,∠A+∠C=80°,则∠D的度数是( )
A.80° B.40° C.70° D.140°
3.(2024 贵州)如图, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.AB=BC B.AD=BC C.OA=OB D.AC⊥BD
4.(2024 乐山)如图,下列条件中不能判定四边形ABCD为平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC C.AO=CO,BO=DO D.AB∥DC,AD=BC
5.(2025 长治一模)如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,∠BAD=135°,∠ACD=80°,∠CBD=20°,则∠COD的度数为( )
A.75° B.53° C.85° D.90°
6.(2024 武汉)小美同学按如下步骤作四边形ABCD;(1)画∠MAN;(2)以点A为圆心,1个单位长为半径画弧,分别交AM,AN于点B,D;(3)分别以点B,D为圆心,1个单位长为半径画弧,两弧交于点C;(4)连接BC,CD,BD.若∠A=44°,则∠CBD的大小是( )
A.64° B.66° C.68° D.70°
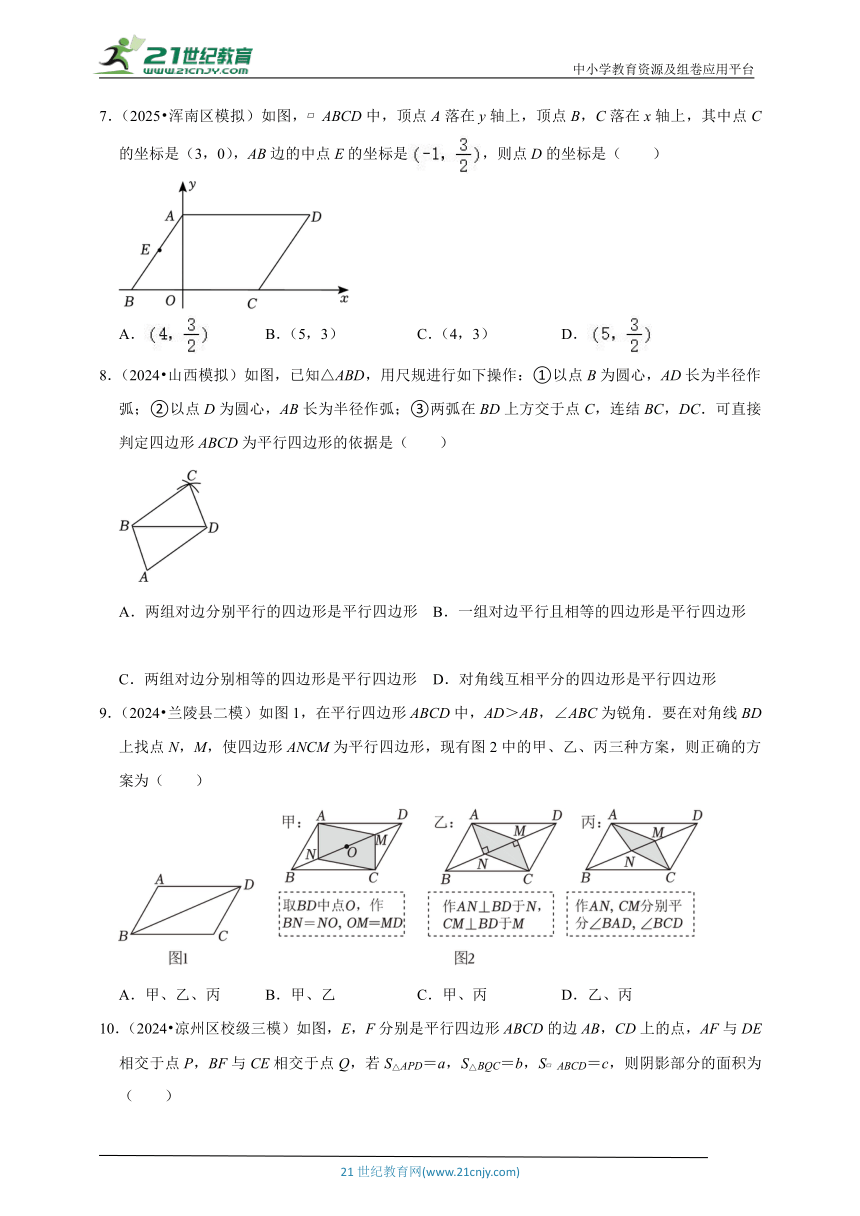
7.(2025 浑南区模拟)如图, ABCD中,顶点A落在y轴上,顶点B,C落在x轴上,其中点C的坐标是(3,0),AB边的中点E的坐标是,则点D的坐标是( )
A. B.(5,3) C.(4,3) D.
8.(2024 山西模拟)如图,已知△ABD,用尺规进行如下操作:①以点B为圆心,AD长为半径作弧;②以点D为圆心,AB长为半径作弧;③两弧在BD上方交于点C,连结BC,DC.可直接判定四边形ABCD为平行四边形的依据是( )
A.两组对边分别平行的四边形是平行四边形 B.一组对边平行且相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形 D.对角线互相平分的四边形是平行四边形
9.(2024 兰陵县二模)如图1,在平行四边形ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案为( )
A.甲、乙、丙 B.甲、乙 C.甲、丙 D.乙、丙
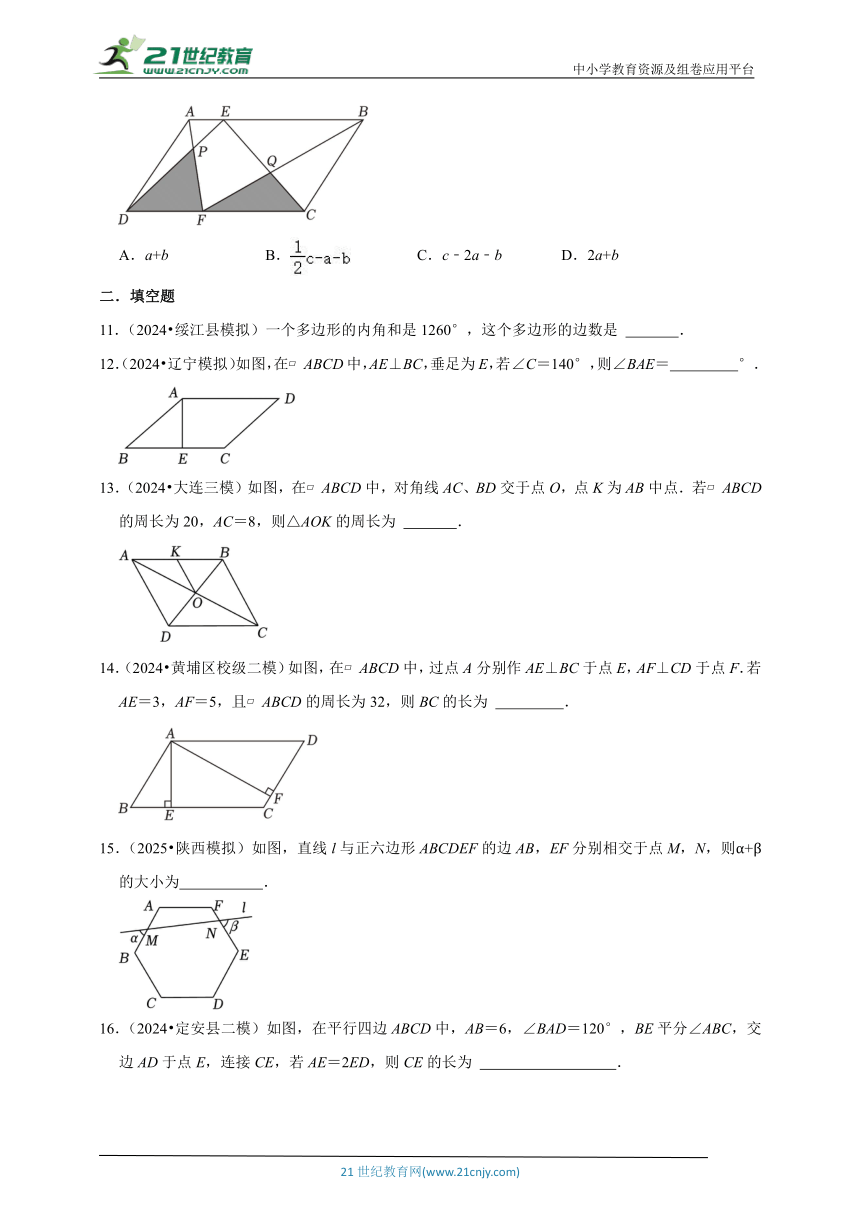
10.(2024 凉州区校级三模)如图,E,F分别是平行四边形ABCD的边AB,CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=a,S△BQC=b,S ABCD=c,则阴影部分的面积为( )
A.a+b B. C.c﹣2a﹣b D.2a+b
二.填空题
11.(2024 绥江县模拟)一个多边形的内角和是1260°,这个多边形的边数是 .
12.(2024 辽宁模拟)如图,在 ABCD中,AE⊥BC,垂足为E,若∠C=140°,则∠BAE= °.
13.(2024 大连三模)如图,在 ABCD中,对角线AC、BD交于点O,点K为AB中点.若 ABCD的周长为20,AC=8,则△AOK的周长为 .
14.(2024 黄埔区校级二模)如图,在 ABCD中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.若AE=3,AF=5,且 ABCD的周长为32,则BC的长为 .
15.(2025 陕西模拟)如图,直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,则α+β的大小为 .
16.(2024 定安县二模)如图,在平行四边ABCD中,AB=6,∠BAD=120°,BE平分∠ABC,交边AD于点E,连接CE,若AE=2ED,则CE的长为 .
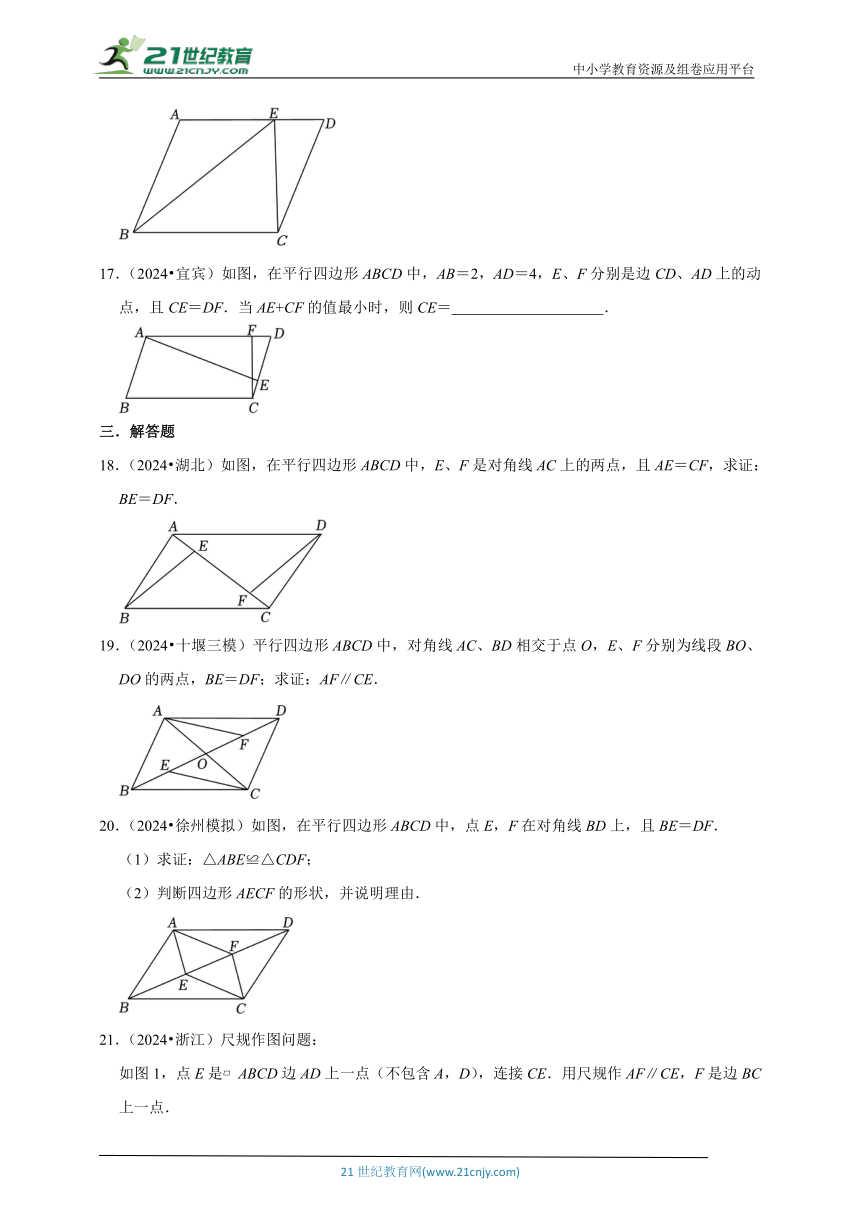
17.(2024 宜宾)如图,在平行四边形ABCD中,AB=2,AD=4,E、F分别是边CD、AD上的动点,且CE=DF.当AE+CF的值最小时,则CE= .
三.解答题
18.(2024 湖北)如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:BE=DF.
19.(2024 十堰三模)平行四边形ABCD中,对角线AC、BD相交于点O,E、F分别为线段BO、DO的两点,BE=DF;求证:AF∥CE.
20.(2024 徐州模拟)如图,在平行四边形ABCD中,点E,F在对角线BD上,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)判断四边形AECF的形状,并说明理由.
21.(2024 浙江)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.
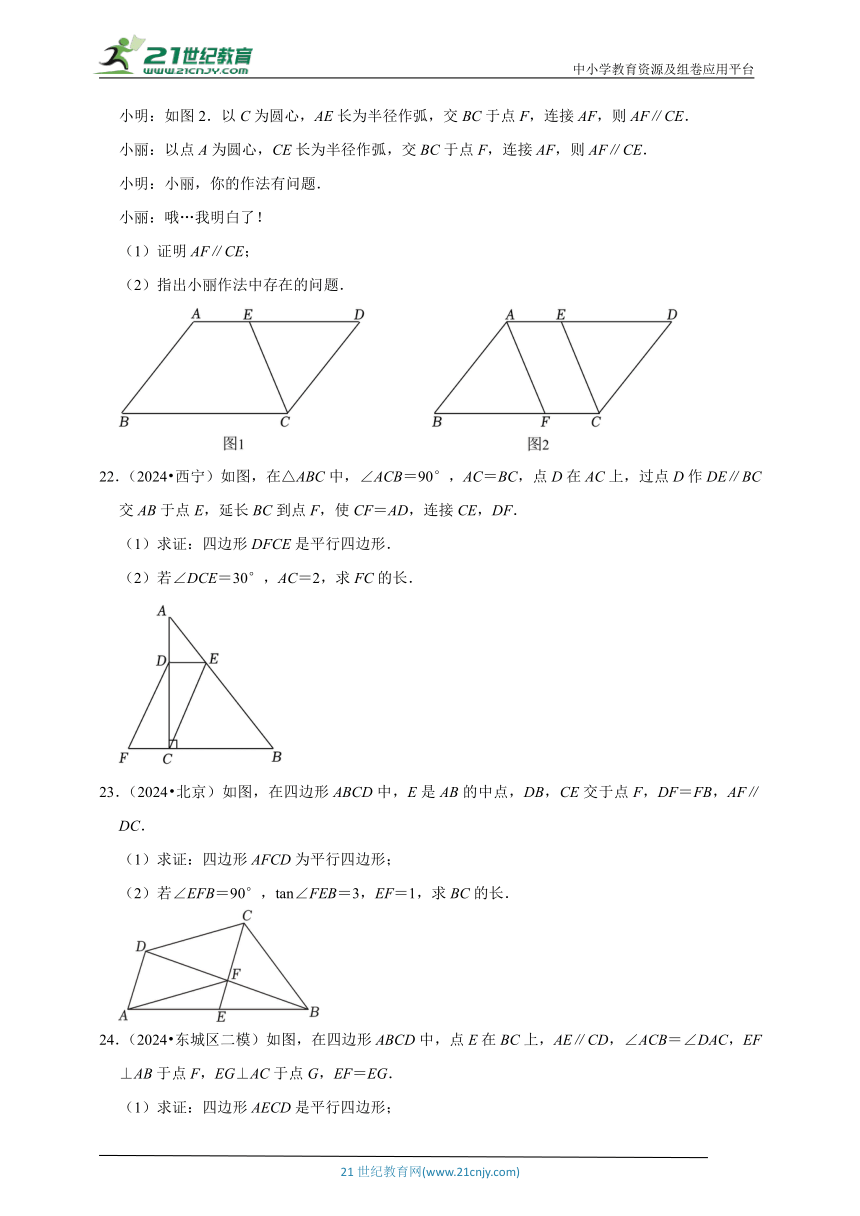
小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦…我明白了!
(1)证明AF∥CE;
(2)指出小丽作法中存在的问题.
22.(2024 西宁)如图,在△ABC中,∠ACB=90°,AC=BC,点D在AC上,过点D作DE∥BC交AB于点E,延长BC到点F,使CF=AD,连接CE,DF.
(1)求证:四边形DFCE是平行四边形.
(2)若∠DCE=30°,AC=2,求FC的长.
23.(2024 北京)如图,在四边形ABCD中,E是AB的中点,DB,CE交于点F,DF=FB,AF∥DC.
(1)求证:四边形AFCD为平行四边形;
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
24.(2024 东城区二模)如图,在四边形ABCD中,点E在BC上,AE∥CD,∠ACB=∠DAC,EF⊥AB于点F,EG⊥AC于点G,EF=EG.
(1)求证:四边形AECD是平行四边形;
(2)若CD=4,∠B=45°,∠CEG=15°,求AB的长.
答案与解析
一.选择题
1.(2025 济南模拟)已知一个多边形的内角和等于外角和,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
【点拨】设多边形的边数为n,则根据多边形的内角和公式与多边形的外角和为360°,列方程解答.
【解析】解:设多边形的边数为n,根据题意列方程得,
(n﹣2) 180°=360°,
n﹣2=2,
n=4.
故选:B.
【点睛】本题考查了多边形的内角与外角,解题的关键是利用多边形的内角和公式并熟悉多边形的外角和为360°.
2.(2024 锦江区校级模拟)在 ABCD中,∠A+∠C=80°,则∠D的度数是( )
A.80° B.40° C.70° D.140°
【点拨】由平行四边形的性质可得∠A=∠C,AB∥CD,结合∠A+∠C=80°得出∠A=∠C=40°,再由平行线的性质计算即可得出答案.
【解析】解:如图,
∵四边形ABCD为平行四边形,
∴∠A=∠C,AB∥CD,
∵∠A+∠C=80°,
∴∠A=∠C=40°,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠D=180°﹣∠A=140°,
故选:D.
【点睛】本题考查了平行四边形的性质,关键是平行四边形性质的应用.
3.(2024 贵州)如图, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.AB=BC B.AD=BC C.OA=OB D.AC⊥BD
【点拨】利用平行四边形的性质一一判断即可解决问题.
【解析】解:A、平行四边形的邻边不相等,无法得到AB=BC,故此选项不合题意;
B、因为平行四边形的对边相等,故AD=BC,故此选项符合题意;
C、平行四边形的对角线不相等,无法得出AO=BO,故此选项不合题意;
D、平行四边形的对角线不垂直,无法得到AC⊥BD,故此选项不合题意.
故选:B.
【点睛】本题考查平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.
4.(2024 乐山)如图,下列条件中不能判定四边形ABCD为平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC C.AO=CO,BO=DO D.AB∥DC,AD=BC
【点拨】根据平行四边形的判断定理分别作出判断得出即可.
【解析】解:A、根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;
B、根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;
C、根据平行四边形的判定定理:对角线互相平分的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;
D、一组对边平行,另一组对边相等,可能是等腰梯形,故不能判断这个四边形是平行四边形,符合题意;
故选:D.
【点睛】本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
5.(2025 长治一模)如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,∠BAD=135°,∠ACD=80°,∠CBD=20°,则∠COD的度数为( )
A.75° B.53° C.85° D.90°
【点拨】根据平行线的性质求出∠OCB=55°,再根据三角形外角的性质可得结论.
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAC=∠ACD=80°,
∵∠BAD=135°,
∴∠CAD=∠BAD﹣∠BAC=135°﹣80°=55°,
∵AD∥BC,
∴∠BCA=∠CAD=55°,
∵∠CBD=20°,
∴∠COD=∠CBD+∠BCA=20°+55°=75°,
故选:A.
【点睛】本题主要考查平行线的性质,掌握其性质是解题的关键.
6.(2024 武汉)小美同学按如下步骤作四边形ABCD;(1)画∠MAN;(2)以点A为圆心,1个单位长为半径画弧,分别交AM,AN于点B,D;(3)分别以点B,D为圆心,1个单位长为半径画弧,两弧交于点C;(4)连接BC,CD,BD.若∠A=44°,则∠CBD的大小是( )
A.64° B.66° C.68° D.70°
【点拨】由(1)(2)(3)可知四边形ABCD是菱形,然后根据菱形的性质和三角形内角和定理求出答案即可.
【解析】解:由(1)(2)(3)可知四边形ABCD是菱形,
∴AB=AD,BC∥AD,
∴∠ABD=∠ADB=∠CBD,
∵∠A=44°,
∴∠ABD+∠ADB=180°﹣∠A=180°﹣44°=136°,
∴∠ABD=∠ADB=∠CBD=68°,
故选:C.
【点睛】本题主要考查了多边形的内角与外角和菱形的判定与性质,解题关键是根据已知条件中的作图判定四边形ABCD的形状.
7.(2025 浑南区模拟)如图, ABCD中,顶点A落在y轴上,顶点B,C落在x轴上,其中点C的坐标是(3,0),AB边的中点E的坐标是,则点D的坐标是( )
A. B.(5,3) C.(4,3) D.
【点拨】根据点E的坐标,可以得到点A和点B的坐标,然后根据平行四边形的性质,可以得到点D的坐标.
【解析】解:∵AB边的中点E的坐标是,
∴点B的坐标为(﹣2,0),点A的坐标为(0,3),
∵点C的坐标是(3,0),
∴BC=3﹣(﹣2)=5,
∵四边形ABCD是平行四边形,
∴AD=BC=5,
∴点D的坐标为(5,3),
故选:B.
【点睛】本题考查平行四边形的性质、坐标与图形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
8.(2024 山西模拟)如图,已知△ABD,用尺规进行如下操作:①以点B为圆心,AD长为半径作弧;②以点D为圆心,AB长为半径作弧;③两弧在BD上方交于点C,连结BC,DC.可直接判定四边形ABCD为平行四边形的依据是( )
A.两组对边分别平行的四边形是平行四边形 B.一组对边平行且相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形 D.对角线互相平分的四边形是平行四边形
【点拨】由题意可知,BC=AD,DC=AB,再由平行四边形的判定即可得出结论.
【解析】解:由题意可知,BC=AD,DC=AB,
∴四边形ABCD为平行四边形,
故选:C.
【点睛】本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
9.(2024 兰陵县二模)如图1,在平行四边形ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案为( )
A.甲、乙、丙 B.甲、乙 C.甲、丙 D.乙、丙
【点拨】方案甲:连接AC,由平行四边形的性质得OB=OD,OA=OC,则NO=OM,得四边形ANCM为平行四边形;
方案乙:证△ABN≌△CDM(AAS),得AN=CM,再由AN∥CM,得四边形ANCM为平行四边形;
方案丙:证△ABN≌△CDM(ASA),得AN=CM,∠ANB=∠CMD,则∠ANM=∠CMN,证出AN∥CM,得四边形ANCM为平行四边形.
【解析】解:方案甲:如图,连接AC,
∵四边形ABCD是平行四边形,O为BD的中点,
∴OB=OD,OA=OC,
∵BN=NO,OM=MD,
∴NO=OM,
∴四边形ANCM为平行四边形,故方案甲正确;
方案乙:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABN=∠CDM,
∵AN⊥BD,CM⊥BD,
∴AN∥CM,∠ANB=∠CMD=90°,
在△ABN和△CDM中,
,
∴△ABN≌△CDM(AAS),
∴AN=CM,
又∵AN∥CM,
∴四边形ANCM为平行四边形,故方案乙正确;
方案丙:∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AB=CD,AB∥CD,
∴∠ABN=∠CDM,
∵AN平分∠BAD,CM平分∠BCD,
∴∠BAN=∠DCM,
在△ABN和△CDM中,
,
∴△ABN≌△CDM(ASA),
∴AN=CM,∠ANB=∠CMD,
∵∠ANB+∠ANM=180°,∠CMD+∠CMN=180°,
∴∠ANM=∠CMN,
∴AN∥CM,
∴四边形ANCM为平行四边形,故方案丙正确;
故选:A.
【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、平行线的判定与性质、角平分线的定义等知识;熟练掌握平行四边形的判定与性质是解题的关键.
10.(2024 凉州区校级三模)如图,E,F分别是平行四边形ABCD的边AB,CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=a,S△BQC=b,S ABCD=c,则阴影部分的面积为( )
A.a+b B. C.c﹣2a﹣b D.2a+b
【点拨】根据平行四边形的面积与三角形的面积公式可得三角形EDC的面积,连接E、F两点,由三角形的面积公式我们可以推出S△EFQ=S△BCQ,S△EFD=S△ADF,所以S△EFG=S△BCQ,S△EFP=S△ADP,因此可以推出四边形EPFQ的面积就是S△APD+S△BQC.再根据面积差可得答案.
【解析】解:连接E、F两点,过点E作EM⊥DC于点M,
∵S△DEC=,S ABCD=DC EM=c,
∴S△DEC=c,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△ADP,
∵S△APD=a,S△BQC=b,
∴S四边形EPFQ=a+b,
故阴影部分的面积为=S△DEC﹣S四边形EPFQ=c﹣a﹣b.
故选:B.
【点睛】本题主要考查平行四边形的性质,三角形的面积,解题的关键在于求出各三角形之间的面积关系.
二.填空题
11.(2024 绥江县模拟)一个多边形的内角和是1260°,这个多边形的边数是 9 .
【点拨】由多边形内角和定理:(n﹣2) 180°,可求多边形的边数.
【解析】解:设这个多边形的边数是n,
由题意得:(n﹣2) 180°=1260°,
∴n=9,
故答案为:9.
【点睛】本题考查多边形的有关知识,关键是掌握多边形的内角和定理.
12.(2024 辽宁模拟)如图,在 ABCD中,AE⊥BC,垂足为E,若∠C=140°,则∠BAE= 50 °.
【点拨】由平行四边形的性质推出AB∥CD,由平行线的性质推出∠B+∠C=180°,求出∠B=40°,由垂直的定义得到∠AEB=90°,即可求出∠BAE=90°﹣40°=50°.
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=140°,
∴∠B=40°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=90°﹣40°=50°.
故答案为:50°.
【点睛】本题考查平行四边形的性质,关键是由平行四边形的性质求出∠B=40°.
13.(2024 大连三模)如图,在 ABCD中,对角线AC、BD交于点O,点K为AB中点.若 ABCD的周长为20,AC=8,则△AOK的周长为 9 .
【点拨】根据平行四边形的对边相等和对角线互相平分可得,OA=OC,DO=BO,点K为AB中点,可得OK是△ABC的中位线,可得OK=BC.从而得到△AOK的周长.
【解析】解:∵四边形ABCD是平行四边形,其周长为20,
∴OA=OC,OB=OD,AB+BC=10,
又∵点K为AB中点,
∴OK是△ABC的中位线,AK=AB,
∴OK=BC,
∴△AOK的周长=×(AB+BC+AC)=×(10+8)=9,
故答案为:9.
【点睛】本题主要考查平行四边形的性质及三角形中位线的性质的应用.解题时注意:平行四边形的对角线互相平分.
14.(2024 黄埔区校级二模)如图,在 ABCD中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.若AE=3,AF=5,且 ABCD的周长为32,则BC的长为 10 .
【点拨】由平行四边形的性质得出S ABCD=BC AE=CD AF,又由AE=3,AF=5,可得3BC=5CD,又由 ABCD的周长为32,可得BC+CD=16,继而求得答案.
【解析】解:∵ ABCD的周长为32,
∴BC+CD=16,
∵ ABCD中,AE⊥BC,AF⊥CD,
∴S ABCD=BC AE=CD AF
∵AE=3,AF=5,
∴3BC=5CD,
∴BC=10,CD=6,
故答案为:10.
【点睛】此题考查了平行四边形的性质以及平行四边形的面积公式运用,熟练掌握平行四边形的性质是解题的关键.
15.(2025 陕西模拟)如图,直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,则α+β的大小为 120° .
【点拨】先根据正六边形的内角和可得∠A=∠F=120°,再根据四边形的内角和可得∠AMN+∠FNM=120°,然后根据对顶角相等可得∠AMN=α,∠FNM=β,由此即可得.
【解析】解:,
∵在四边形AMNF中,∠AMN+∠FNM+∠A+∠F=360°,
∴∠AMN+∠FNM=360°﹣(∠A+∠F)=120°,
由对顶角相等得:∠AMN=α,∠FNM=β,
∴α+β=∠AMN+∠FNM=120°,
故答案为:120°.
【点睛】本题考查了正多边形的内角和、四边形的内角和,熟练掌握多边形的内角和是解题关键.
16.(2024 定安县二模)如图,在平行四边ABCD中,AB=6,∠BAD=120°,BE平分∠ABC,交边AD于点E,连接CE,若AE=2ED,则CE的长为 3 .
【点拨】由平行四边形的性质推出AD∥BC,AB∥CD,CD=AB=6,得到∠AEB=∠EBC,由角平分线定义得到∠ABE=∠EBC,因此∠AEB=∠ABE,推出AE=AB=6,求出DE=3,由平行线的性质求出∠D=60°,由含30度角的直角三角形的性质得到DH=DE=,求出EH=DH=,得到CH=CD﹣DH=,由勾股定理求出CE==3.
【解析】解:过E作EH⊥CD于H,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,CD=AB=6,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠AEB=∠ABE,
∴AE=AB=6,
∵AE=2DE,
∴DE=3,
∵AB∥CD,
∴∠A+∠D=180°,
∵∠A=120°,
∴∠D=60°,
∴∠DEH=90°﹣60°=30°,
∴DH=DE=,
∴EH=DH=,
∵CH=CD﹣DH=,
∴CE==3.
故答案为:3.
【点睛】本题考查平行四边形的性质,含30度角的直角三角形,勾股定理,关键是由平行线的性质,角平分线定义得到AE=AB,由含30度角的直角三角形的性质求出DH,EH的长,由勾股定理即可求出CE的长.
17.(2024 宜宾)如图,在平行四边形ABCD中,AB=2,AD=4,E、F分别是边CD、AD上的动点,且CE=DF.当AE+CF的值最小时,则CE= .
【点拨】由“SAS”可证△CDF≌△HCE,可得CF=EH,则AE+CF=AE+EH,即当点A,点E,点H三点共线时,AE+CF有最小值,通过证明△CEH∽△BAH,可得△CEH∽△BAH,即可求解.
【解析】解:如图,延长BC至H,使CH=CD,连接EH,
∵四边形ABCD是平行四边形,
∴AD=BC=4,AB=CD=2,AD∥BC,
∴∠D=∠DCH,
又∵CD=CH,DF=CE,
∴△CDF≌△HCE(SAS),
∴CF=EH,
∴AE+CF=AE+EH,
∴当点A,点E,点H三点共线时,AE+CF有最小值,
此时:∵CD∥AB,
∴△CEH∽△BAH,
∴,
∴=,
∴CE=,
故答案为:.
【点睛】本题考查了平行四边形的性质,全等三角形的判定和性质,相似三角形的判定和性质,添加恰当辅助线构造全等三角形是解题的关键.
三.解答题
18.(2024 湖北)如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:BE=DF.
【点拨】由平行四边形的性质可得AB∥CD,AB=CD即∠BAE=∠DCF,根据SAS可得△ABE≌△CDF,最后根据全等三角形的性质即可解答.
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
【点睛】本题主要考查了平行四边形的性质、全等三角形的判定与性质等知识点,证的△ABE≌△CDF是解答本题的关键.
19.(2024 十堰三模)平行四边形ABCD中,对角线AC、BD相交于点O,E、F分别为线段BO、DO的两点,BE=DF;求证:AF∥CE.
【点拨】由平行四边形的性质得OD=OB,OA=OC,而BE=DF,可推导出OF=OE,即可根据“SAS”证明△AOF≌△COE,得∠AFO=∠CEO,则AF∥CE.
【解析】证明:∵四边形ABCD是平行四边形,对角线AC、BD相交于点O,
∴OD=OB,OA=OC,
∵BE=DF,
∴OD﹣DF=OB﹣BE,
∴OF=OE,
在△AOF和△COE中,
,
∴△AOF≌△COE(SAS),
∴∠AFO=∠CEO,
∴AF∥CE.
【点睛】此题重点考查平行四边形的性质、全等三角形的判定与性质、平行线的判定等知识,证明△AOF≌△COE是解题的关键.
20.(2024 徐州模拟)如图,在平行四边形ABCD中,点E,F在对角线BD上,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)判断四边形AECF的形状,并说明理由.
【点拨】(1)根据平行四边形的性质证明△ABE≌△CDF即可;
(2)证明△ADF≌△CBE得出AF=CE,即可作出判断.
【解析】(1)证明:如图,∵在平行四边形ABCD中,AB=CD,AB∥CD,
∴∠ABD=∠CDB,
在ABE和CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:四边形AECF是平行四边形,理由:
∵△ABE≌△CDF,
∴AE=CF,
又AD=BC,AD∥BC,
∴∠ADB=∠CBD,
又∵BE=DF,
∴△ADF≌△CBE(SAS),
∴AF=CE,
∴四边形AECF是平行四边形.
【点睛】本题考查了平行四边形的判定与性质、全等三角形的性质和判定,解答该题的关键是熟练掌握平行四边形的性质与判定.
21.(2024 浙江)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦…我明白了!
(1)证明AF∥CE;
(2)指出小丽作法中存在的问题.
【点拨】(1)根据小明的作法知,CF=AE,根据平行四边形的性质求出AD∥BC,根据“一组对边平行且相等的四边形是平行四边形”求出四边形AFCE是平行四边形,根据“平行四边形的对边互相平行”即可得证;
(2)以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
【解析】(1)证明:根据小明的作法知,CF=AE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵CF=AE,
∴四边形AFCE是平行四边形,
∴AF∥CE;
(2)解:以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
故小丽的作法有问题.
【点睛】此题考查了平行四边形的判定与性质,熟记平行四边形的判定定理与性质定理是解题的关键.
22.(2024 西宁)如图,在△ABC中,∠ACB=90°,AC=BC,点D在AC上,过点D作DE∥BC交AB于点E,延长BC到点F,使CF=AD,连接CE,DF.
(1)求证:四边形DFCE是平行四边形.
(2)若∠DCE=30°,AC=2,求FC的长.
【点拨】(1)由等腰直角三角形的性质得∠A=∠B=45°,进而证明∠A=∠AED,得AD=DE,再证明DE=CF,然后由平行四边形的判定即可得出结论;
(2)由平行四边形的性质得FC=DE,设AD=DE=FC=x,则DC=AC﹣AD=2﹣x,再由含30°角的直角三角形的性质得CE=2DE=2x,然后由勾股定理得出方程,解方程即可.
【解析】(1)证明:∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵DE∥BC,
∴∠ADE=∠ACB=90°,∠AED=∠B=45°,
∴∠A=∠AED,
∴AD=DE,
∵CF=AD,
∴DE=CF,
又∵DE∥FC,
∴四边形DFCE是平行四边形;
(2)解:由(1)可知,四边形DFCE是平行四边形,
∴FC=DE,
设AD=DE=FC=x,则DC=AC﹣AD=2﹣x,
由(1)可知,∠ADE=90°,
∴∠CDE=90°,
在Rt△DEC中,∠DCE=30°,
∴CE=2DE=2x,
由勾股定理得:DE2+CD2=CE2,
即x2+(2﹣x)2=(2x)2,
解得:x=﹣1,x2=﹣﹣1(不符合题意,舍去),
∴FC=﹣1.
【点睛】本题考查了平行四边形的判定与性质、等腰直角三角形的性质、平行线的性质、含30°角的直角三角形的性质以及勾股定理等知识,熟练掌握平行四边形的判定与性质是解题的关键.
23.(2024 北京)如图,在四边形ABCD中,E是AB的中点,DB,CE交于点F,DF=FB,AF∥DC.
(1)求证:四边形AFCD为平行四边形;
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
【点拨】(1)根据三角形中位线定理得到EF∥AD,根据平行四边形的判定定理得到结论;
(2)根据三角形中位线定理求得AD=2EF=2,根据三角函数的定义得到BF=3EF=3,求得DF=BF=3,根据勾股定理得到AF==,根据平行四边形的性质得到CD=AF=,根据线段垂直平分线的性质得到结论.
【解析】(1)证明:∵E是AB的中点,
∴AE=BE,
∵DF=BF,
∴EF是△ABD的中位线,
∴EF∥AD,
∴CF∥AD,
∵AF∥CD,
∴四边形AFCD为平行四边形;
(2)解:由(1)知,EF是△ABD的中位线,
∴AD=2EF=2,
∵∠EFB=90°,tan∠FEB=3,
∴BF=3EF=3,
∵DF=FB,
∴DF=BF=3,
∵AD∥CE,
∴∠ADF=∠EFB=90°,
∴AF==,
∵四边形AFCD为平行四边形,
∴CD=AF=,
∵DF=BF,CE⊥BD,
∴BC=CD=.
【点睛】本题考查了平行四边形的判定和性质,解直角三角形,三角形中位线定理,勾股定理,熟练掌握平行四边形的判定和性质定理是解题的关键.
24.(2024 东城区二模)如图,在四边形ABCD中,点E在BC上,AE∥CD,∠ACB=∠DAC,EF⊥AB于点F,EG⊥AC于点G,EF=EG.
(1)求证:四边形AECD是平行四边形;
(2)若CD=4,∠B=45°,∠CEG=15°,求AB的长.
【点拨】(1)证明AD∥CE,再由平行四边形的判定即可得出结论;
(2)由平行四边形的性质得AE=CD=4,进而证明Rt△AFE≌Rt△AGE(HL),再证明△BEF是等腰直角三角形,然后证明由含30°的直角三角形的性质得BF=EF=2,进而由勾股定理求出AF的长,即可解决问题.
【解析】(1)证明:∵∠ACB=∠DAC,
∴AD∥CE,
∵AE∥CD,
∴四边形AECD是平行四边形;
(2)解:由(1)可知,四边形AECD是平行四边形,
∴AE=CD=4,
∵EF⊥AB,EG⊥AC,
∴∠AFE=∠AGE=90°,
在Rt△AFE和Rt△AGE中,
,
∴Rt△AFE≌Rt△AGE(HL),
∴∠AEF=∠AEG,
∵∠BFE=180°﹣90°=90°,∠B=45°,
∴△BEF是等腰直角三角形,
∴BF=EF,∠BEF=45°,
∴∠FEG=180°﹣∠BEF﹣∠CEG=180°﹣45°﹣15°=120°,
∴∠AEF=∠AEG=∠FEG=60°,
∴∠EAF=90°﹣∠AEF=30°,
∴BF=EF=AE=2,
∴AF===2,
∴AB=AF+BF=2+2.
【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、平行线的判定、含30°角的直角三角形的性质以及勾股定理等知识,熟练掌握平行四边形的判定与性质和全等三角形的判定与性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题21 多边形与平行四边形
一.选择题
1.(2025 济南模拟)已知一个多边形的内角和等于外角和,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
2.(2024 锦江区校级模拟)在 ABCD中,∠A+∠C=80°,则∠D的度数是( )
A.80° B.40° C.70° D.140°
3.(2024 贵州)如图, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.AB=BC B.AD=BC C.OA=OB D.AC⊥BD
4.(2024 乐山)如图,下列条件中不能判定四边形ABCD为平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC C.AO=CO,BO=DO D.AB∥DC,AD=BC
5.(2025 长治一模)如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,∠BAD=135°,∠ACD=80°,∠CBD=20°,则∠COD的度数为( )
A.75° B.53° C.85° D.90°
6.(2024 武汉)小美同学按如下步骤作四边形ABCD;(1)画∠MAN;(2)以点A为圆心,1个单位长为半径画弧,分别交AM,AN于点B,D;(3)分别以点B,D为圆心,1个单位长为半径画弧,两弧交于点C;(4)连接BC,CD,BD.若∠A=44°,则∠CBD的大小是( )
A.64° B.66° C.68° D.70°
7.(2025 浑南区模拟)如图, ABCD中,顶点A落在y轴上,顶点B,C落在x轴上,其中点C的坐标是(3,0),AB边的中点E的坐标是,则点D的坐标是( )
A. B.(5,3) C.(4,3) D.
8.(2024 山西模拟)如图,已知△ABD,用尺规进行如下操作:①以点B为圆心,AD长为半径作弧;②以点D为圆心,AB长为半径作弧;③两弧在BD上方交于点C,连结BC,DC.可直接判定四边形ABCD为平行四边形的依据是( )
A.两组对边分别平行的四边形是平行四边形 B.一组对边平行且相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形 D.对角线互相平分的四边形是平行四边形
9.(2024 兰陵县二模)如图1,在平行四边形ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案为( )
A.甲、乙、丙 B.甲、乙 C.甲、丙 D.乙、丙
10.(2024 凉州区校级三模)如图,E,F分别是平行四边形ABCD的边AB,CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=a,S△BQC=b,S ABCD=c,则阴影部分的面积为( )
A.a+b B. C.c﹣2a﹣b D.2a+b
二.填空题
11.(2024 绥江县模拟)一个多边形的内角和是1260°,这个多边形的边数是 .
12.(2024 辽宁模拟)如图,在 ABCD中,AE⊥BC,垂足为E,若∠C=140°,则∠BAE= °.
13.(2024 大连三模)如图,在 ABCD中,对角线AC、BD交于点O,点K为AB中点.若 ABCD的周长为20,AC=8,则△AOK的周长为 .
14.(2024 黄埔区校级二模)如图,在 ABCD中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.若AE=3,AF=5,且 ABCD的周长为32,则BC的长为 .
15.(2025 陕西模拟)如图,直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,则α+β的大小为 .
16.(2024 定安县二模)如图,在平行四边ABCD中,AB=6,∠BAD=120°,BE平分∠ABC,交边AD于点E,连接CE,若AE=2ED,则CE的长为 .
17.(2024 宜宾)如图,在平行四边形ABCD中,AB=2,AD=4,E、F分别是边CD、AD上的动点,且CE=DF.当AE+CF的值最小时,则CE= .
三.解答题
18.(2024 湖北)如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:BE=DF.
19.(2024 十堰三模)平行四边形ABCD中,对角线AC、BD相交于点O,E、F分别为线段BO、DO的两点,BE=DF;求证:AF∥CE.
20.(2024 徐州模拟)如图,在平行四边形ABCD中,点E,F在对角线BD上,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)判断四边形AECF的形状,并说明理由.
21.(2024 浙江)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦…我明白了!
(1)证明AF∥CE;
(2)指出小丽作法中存在的问题.
22.(2024 西宁)如图,在△ABC中,∠ACB=90°,AC=BC,点D在AC上,过点D作DE∥BC交AB于点E,延长BC到点F,使CF=AD,连接CE,DF.
(1)求证:四边形DFCE是平行四边形.
(2)若∠DCE=30°,AC=2,求FC的长.
23.(2024 北京)如图,在四边形ABCD中,E是AB的中点,DB,CE交于点F,DF=FB,AF∥DC.
(1)求证:四边形AFCD为平行四边形;
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
24.(2024 东城区二模)如图,在四边形ABCD中,点E在BC上,AE∥CD,∠ACB=∠DAC,EF⊥AB于点F,EG⊥AC于点G,EF=EG.
(1)求证:四边形AECD是平行四边形;
(2)若CD=4,∠B=45°,∠CEG=15°,求AB的长.
答案与解析
一.选择题
1.(2025 济南模拟)已知一个多边形的内角和等于外角和,则这个多边形是( )
A.三角形 B.四边形 C.五边形 D.六边形
【点拨】设多边形的边数为n,则根据多边形的内角和公式与多边形的外角和为360°,列方程解答.
【解析】解:设多边形的边数为n,根据题意列方程得,
(n﹣2) 180°=360°,
n﹣2=2,
n=4.
故选:B.
【点睛】本题考查了多边形的内角与外角,解题的关键是利用多边形的内角和公式并熟悉多边形的外角和为360°.
2.(2024 锦江区校级模拟)在 ABCD中,∠A+∠C=80°,则∠D的度数是( )
A.80° B.40° C.70° D.140°
【点拨】由平行四边形的性质可得∠A=∠C,AB∥CD,结合∠A+∠C=80°得出∠A=∠C=40°,再由平行线的性质计算即可得出答案.
【解析】解:如图,
∵四边形ABCD为平行四边形,
∴∠A=∠C,AB∥CD,
∵∠A+∠C=80°,
∴∠A=∠C=40°,
∵AB∥CD,
∴∠A+∠D=180°,
∴∠D=180°﹣∠A=140°,
故选:D.
【点睛】本题考查了平行四边形的性质,关键是平行四边形性质的应用.
3.(2024 贵州)如图, ABCD的对角线AC与BD相交于点O,则下列结论一定正确的是( )
A.AB=BC B.AD=BC C.OA=OB D.AC⊥BD
【点拨】利用平行四边形的性质一一判断即可解决问题.
【解析】解:A、平行四边形的邻边不相等,无法得到AB=BC,故此选项不合题意;
B、因为平行四边形的对边相等,故AD=BC,故此选项符合题意;
C、平行四边形的对角线不相等,无法得出AO=BO,故此选项不合题意;
D、平行四边形的对角线不垂直,无法得到AC⊥BD,故此选项不合题意.
故选:B.
【点睛】本题考查平行四边形的性质,熟练掌握平行四边形的性质是解题的关键.
4.(2024 乐山)如图,下列条件中不能判定四边形ABCD为平行四边形的是( )
A.AB∥DC,AD∥BC B.AB=DC,AD=BC C.AO=CO,BO=DO D.AB∥DC,AD=BC
【点拨】根据平行四边形的判断定理分别作出判断得出即可.
【解析】解:A、根据平行四边形的判定定理:两组对边分别平行的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;
B、根据平行四边形的判定定理:两组对边分别相等的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;
C、根据平行四边形的判定定理:对角线互相平分的四边形是平行四边形,故能判断这个四边形是平行四边形,不符合题意;
D、一组对边平行,另一组对边相等,可能是等腰梯形,故不能判断这个四边形是平行四边形,符合题意;
故选:D.
【点睛】本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
5.(2025 长治一模)如图,四边形ABCD是平行四边形,对角线AC,BD相交于点O,∠BAD=135°,∠ACD=80°,∠CBD=20°,则∠COD的度数为( )
A.75° B.53° C.85° D.90°
【点拨】根据平行线的性质求出∠OCB=55°,再根据三角形外角的性质可得结论.
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,
∴∠BAC=∠ACD=80°,
∵∠BAD=135°,
∴∠CAD=∠BAD﹣∠BAC=135°﹣80°=55°,
∵AD∥BC,
∴∠BCA=∠CAD=55°,
∵∠CBD=20°,
∴∠COD=∠CBD+∠BCA=20°+55°=75°,
故选:A.
【点睛】本题主要考查平行线的性质,掌握其性质是解题的关键.
6.(2024 武汉)小美同学按如下步骤作四边形ABCD;(1)画∠MAN;(2)以点A为圆心,1个单位长为半径画弧,分别交AM,AN于点B,D;(3)分别以点B,D为圆心,1个单位长为半径画弧,两弧交于点C;(4)连接BC,CD,BD.若∠A=44°,则∠CBD的大小是( )
A.64° B.66° C.68° D.70°
【点拨】由(1)(2)(3)可知四边形ABCD是菱形,然后根据菱形的性质和三角形内角和定理求出答案即可.
【解析】解:由(1)(2)(3)可知四边形ABCD是菱形,
∴AB=AD,BC∥AD,
∴∠ABD=∠ADB=∠CBD,
∵∠A=44°,
∴∠ABD+∠ADB=180°﹣∠A=180°﹣44°=136°,
∴∠ABD=∠ADB=∠CBD=68°,
故选:C.
【点睛】本题主要考查了多边形的内角与外角和菱形的判定与性质,解题关键是根据已知条件中的作图判定四边形ABCD的形状.
7.(2025 浑南区模拟)如图, ABCD中,顶点A落在y轴上,顶点B,C落在x轴上,其中点C的坐标是(3,0),AB边的中点E的坐标是,则点D的坐标是( )
A. B.(5,3) C.(4,3) D.
【点拨】根据点E的坐标,可以得到点A和点B的坐标,然后根据平行四边形的性质,可以得到点D的坐标.
【解析】解:∵AB边的中点E的坐标是,
∴点B的坐标为(﹣2,0),点A的坐标为(0,3),
∵点C的坐标是(3,0),
∴BC=3﹣(﹣2)=5,
∵四边形ABCD是平行四边形,
∴AD=BC=5,
∴点D的坐标为(5,3),
故选:B.
【点睛】本题考查平行四边形的性质、坐标与图形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
8.(2024 山西模拟)如图,已知△ABD,用尺规进行如下操作:①以点B为圆心,AD长为半径作弧;②以点D为圆心,AB长为半径作弧;③两弧在BD上方交于点C,连结BC,DC.可直接判定四边形ABCD为平行四边形的依据是( )
A.两组对边分别平行的四边形是平行四边形 B.一组对边平行且相等的四边形是平行四边形
C.两组对边分别相等的四边形是平行四边形 D.对角线互相平分的四边形是平行四边形
【点拨】由题意可知,BC=AD,DC=AB,再由平行四边形的判定即可得出结论.
【解析】解:由题意可知,BC=AD,DC=AB,
∴四边形ABCD为平行四边形,
故选:C.
【点睛】本题考查了平行四边形的判定,熟练掌握平行四边形的判定方法是解题的关键.
9.(2024 兰陵县二模)如图1,在平行四边形ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图2中的甲、乙、丙三种方案,则正确的方案为( )
A.甲、乙、丙 B.甲、乙 C.甲、丙 D.乙、丙
【点拨】方案甲:连接AC,由平行四边形的性质得OB=OD,OA=OC,则NO=OM,得四边形ANCM为平行四边形;
方案乙:证△ABN≌△CDM(AAS),得AN=CM,再由AN∥CM,得四边形ANCM为平行四边形;
方案丙:证△ABN≌△CDM(ASA),得AN=CM,∠ANB=∠CMD,则∠ANM=∠CMN,证出AN∥CM,得四边形ANCM为平行四边形.
【解析】解:方案甲:如图,连接AC,
∵四边形ABCD是平行四边形,O为BD的中点,
∴OB=OD,OA=OC,
∵BN=NO,OM=MD,
∴NO=OM,
∴四边形ANCM为平行四边形,故方案甲正确;
方案乙:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴∠ABN=∠CDM,
∵AN⊥BD,CM⊥BD,
∴AN∥CM,∠ANB=∠CMD=90°,
在△ABN和△CDM中,
,
∴△ABN≌△CDM(AAS),
∴AN=CM,
又∵AN∥CM,
∴四边形ANCM为平行四边形,故方案乙正确;
方案丙:∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AB=CD,AB∥CD,
∴∠ABN=∠CDM,
∵AN平分∠BAD,CM平分∠BCD,
∴∠BAN=∠DCM,
在△ABN和△CDM中,
,
∴△ABN≌△CDM(ASA),
∴AN=CM,∠ANB=∠CMD,
∵∠ANB+∠ANM=180°,∠CMD+∠CMN=180°,
∴∠ANM=∠CMN,
∴AN∥CM,
∴四边形ANCM为平行四边形,故方案丙正确;
故选:A.
【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、平行线的判定与性质、角平分线的定义等知识;熟练掌握平行四边形的判定与性质是解题的关键.
10.(2024 凉州区校级三模)如图,E,F分别是平行四边形ABCD的边AB,CD上的点,AF与DE相交于点P,BF与CE相交于点Q,若S△APD=a,S△BQC=b,S ABCD=c,则阴影部分的面积为( )
A.a+b B. C.c﹣2a﹣b D.2a+b
【点拨】根据平行四边形的面积与三角形的面积公式可得三角形EDC的面积,连接E、F两点,由三角形的面积公式我们可以推出S△EFQ=S△BCQ,S△EFD=S△ADF,所以S△EFG=S△BCQ,S△EFP=S△ADP,因此可以推出四边形EPFQ的面积就是S△APD+S△BQC.再根据面积差可得答案.
【解析】解:连接E、F两点,过点E作EM⊥DC于点M,
∵S△DEC=,S ABCD=DC EM=c,
∴S△DEC=c,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△EFC的FC边上的高与△BCF的FC边上的高相等,
∴S△EFC=S△BCF,
∴S△EFQ=S△BCQ,
同理:S△EFD=S△ADF,
∴S△EFP=S△ADP,
∵S△APD=a,S△BQC=b,
∴S四边形EPFQ=a+b,
故阴影部分的面积为=S△DEC﹣S四边形EPFQ=c﹣a﹣b.
故选:B.
【点睛】本题主要考查平行四边形的性质,三角形的面积,解题的关键在于求出各三角形之间的面积关系.
二.填空题
11.(2024 绥江县模拟)一个多边形的内角和是1260°,这个多边形的边数是 9 .
【点拨】由多边形内角和定理:(n﹣2) 180°,可求多边形的边数.
【解析】解:设这个多边形的边数是n,
由题意得:(n﹣2) 180°=1260°,
∴n=9,
故答案为:9.
【点睛】本题考查多边形的有关知识,关键是掌握多边形的内角和定理.
12.(2024 辽宁模拟)如图,在 ABCD中,AE⊥BC,垂足为E,若∠C=140°,则∠BAE= 50 °.
【点拨】由平行四边形的性质推出AB∥CD,由平行线的性质推出∠B+∠C=180°,求出∠B=40°,由垂直的定义得到∠AEB=90°,即可求出∠BAE=90°﹣40°=50°.
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=140°,
∴∠B=40°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=90°﹣40°=50°.
故答案为:50°.
【点睛】本题考查平行四边形的性质,关键是由平行四边形的性质求出∠B=40°.
13.(2024 大连三模)如图,在 ABCD中,对角线AC、BD交于点O,点K为AB中点.若 ABCD的周长为20,AC=8,则△AOK的周长为 9 .
【点拨】根据平行四边形的对边相等和对角线互相平分可得,OA=OC,DO=BO,点K为AB中点,可得OK是△ABC的中位线,可得OK=BC.从而得到△AOK的周长.
【解析】解:∵四边形ABCD是平行四边形,其周长为20,
∴OA=OC,OB=OD,AB+BC=10,
又∵点K为AB中点,
∴OK是△ABC的中位线,AK=AB,
∴OK=BC,
∴△AOK的周长=×(AB+BC+AC)=×(10+8)=9,
故答案为:9.
【点睛】本题主要考查平行四边形的性质及三角形中位线的性质的应用.解题时注意:平行四边形的对角线互相平分.
14.(2024 黄埔区校级二模)如图,在 ABCD中,过点A分别作AE⊥BC于点E,AF⊥CD于点F.若AE=3,AF=5,且 ABCD的周长为32,则BC的长为 10 .
【点拨】由平行四边形的性质得出S ABCD=BC AE=CD AF,又由AE=3,AF=5,可得3BC=5CD,又由 ABCD的周长为32,可得BC+CD=16,继而求得答案.
【解析】解:∵ ABCD的周长为32,
∴BC+CD=16,
∵ ABCD中,AE⊥BC,AF⊥CD,
∴S ABCD=BC AE=CD AF
∵AE=3,AF=5,
∴3BC=5CD,
∴BC=10,CD=6,
故答案为:10.
【点睛】此题考查了平行四边形的性质以及平行四边形的面积公式运用,熟练掌握平行四边形的性质是解题的关键.
15.(2025 陕西模拟)如图,直线l与正六边形ABCDEF的边AB,EF分别相交于点M,N,则α+β的大小为 120° .
【点拨】先根据正六边形的内角和可得∠A=∠F=120°,再根据四边形的内角和可得∠AMN+∠FNM=120°,然后根据对顶角相等可得∠AMN=α,∠FNM=β,由此即可得.
【解析】解:,
∵在四边形AMNF中,∠AMN+∠FNM+∠A+∠F=360°,
∴∠AMN+∠FNM=360°﹣(∠A+∠F)=120°,
由对顶角相等得:∠AMN=α,∠FNM=β,
∴α+β=∠AMN+∠FNM=120°,
故答案为:120°.
【点睛】本题考查了正多边形的内角和、四边形的内角和,熟练掌握多边形的内角和是解题关键.
16.(2024 定安县二模)如图,在平行四边ABCD中,AB=6,∠BAD=120°,BE平分∠ABC,交边AD于点E,连接CE,若AE=2ED,则CE的长为 3 .
【点拨】由平行四边形的性质推出AD∥BC,AB∥CD,CD=AB=6,得到∠AEB=∠EBC,由角平分线定义得到∠ABE=∠EBC,因此∠AEB=∠ABE,推出AE=AB=6,求出DE=3,由平行线的性质求出∠D=60°,由含30度角的直角三角形的性质得到DH=DE=,求出EH=DH=,得到CH=CD﹣DH=,由勾股定理求出CE==3.
【解析】解:过E作EH⊥CD于H,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,CD=AB=6,
∴∠AEB=∠EBC,
∵BE平分∠ABC,
∴∠ABE=∠EBC,
∴∠AEB=∠ABE,
∴AE=AB=6,
∵AE=2DE,
∴DE=3,
∵AB∥CD,
∴∠A+∠D=180°,
∵∠A=120°,
∴∠D=60°,
∴∠DEH=90°﹣60°=30°,
∴DH=DE=,
∴EH=DH=,
∵CH=CD﹣DH=,
∴CE==3.
故答案为:3.
【点睛】本题考查平行四边形的性质,含30度角的直角三角形,勾股定理,关键是由平行线的性质,角平分线定义得到AE=AB,由含30度角的直角三角形的性质求出DH,EH的长,由勾股定理即可求出CE的长.
17.(2024 宜宾)如图,在平行四边形ABCD中,AB=2,AD=4,E、F分别是边CD、AD上的动点,且CE=DF.当AE+CF的值最小时,则CE= .
【点拨】由“SAS”可证△CDF≌△HCE,可得CF=EH,则AE+CF=AE+EH,即当点A,点E,点H三点共线时,AE+CF有最小值,通过证明△CEH∽△BAH,可得△CEH∽△BAH,即可求解.
【解析】解:如图,延长BC至H,使CH=CD,连接EH,
∵四边形ABCD是平行四边形,
∴AD=BC=4,AB=CD=2,AD∥BC,
∴∠D=∠DCH,
又∵CD=CH,DF=CE,
∴△CDF≌△HCE(SAS),
∴CF=EH,
∴AE+CF=AE+EH,
∴当点A,点E,点H三点共线时,AE+CF有最小值,
此时:∵CD∥AB,
∴△CEH∽△BAH,
∴,
∴=,
∴CE=,
故答案为:.
【点睛】本题考查了平行四边形的性质,全等三角形的判定和性质,相似三角形的判定和性质,添加恰当辅助线构造全等三角形是解题的关键.
三.解答题
18.(2024 湖北)如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF,求证:BE=DF.
【点拨】由平行四边形的性质可得AB∥CD,AB=CD即∠BAE=∠DCF,根据SAS可得△ABE≌△CDF,最后根据全等三角形的性质即可解答.
【解析】解:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(SAS),
∴BE=DF.
【点睛】本题主要考查了平行四边形的性质、全等三角形的判定与性质等知识点,证的△ABE≌△CDF是解答本题的关键.
19.(2024 十堰三模)平行四边形ABCD中,对角线AC、BD相交于点O,E、F分别为线段BO、DO的两点,BE=DF;求证:AF∥CE.
【点拨】由平行四边形的性质得OD=OB,OA=OC,而BE=DF,可推导出OF=OE,即可根据“SAS”证明△AOF≌△COE,得∠AFO=∠CEO,则AF∥CE.
【解析】证明:∵四边形ABCD是平行四边形,对角线AC、BD相交于点O,
∴OD=OB,OA=OC,
∵BE=DF,
∴OD﹣DF=OB﹣BE,
∴OF=OE,
在△AOF和△COE中,
,
∴△AOF≌△COE(SAS),
∴∠AFO=∠CEO,
∴AF∥CE.
【点睛】此题重点考查平行四边形的性质、全等三角形的判定与性质、平行线的判定等知识,证明△AOF≌△COE是解题的关键.
20.(2024 徐州模拟)如图,在平行四边形ABCD中,点E,F在对角线BD上,且BE=DF.
(1)求证:△ABE≌△CDF;
(2)判断四边形AECF的形状,并说明理由.
【点拨】(1)根据平行四边形的性质证明△ABE≌△CDF即可;
(2)证明△ADF≌△CBE得出AF=CE,即可作出判断.
【解析】(1)证明:如图,∵在平行四边形ABCD中,AB=CD,AB∥CD,
∴∠ABD=∠CDB,
在ABE和CDF中,
,
∴△ABE≌△CDF(SAS);
(2)解:四边形AECF是平行四边形,理由:
∵△ABE≌△CDF,
∴AE=CF,
又AD=BC,AD∥BC,
∴∠ADB=∠CBD,
又∵BE=DF,
∴△ADF≌△CBE(SAS),
∴AF=CE,
∴四边形AECF是平行四边形.
【点睛】本题考查了平行四边形的判定与性质、全等三角形的性质和判定,解答该题的关键是熟练掌握平行四边形的性质与判定.
21.(2024 浙江)尺规作图问题:
如图1,点E是 ABCD边AD上一点(不包含A,D),连接CE.用尺规作AF∥CE,F是边BC上一点.
小明:如图2.以C为圆心,AE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小丽:以点A为圆心,CE长为半径作弧,交BC于点F,连接AF,则AF∥CE.
小明:小丽,你的作法有问题.
小丽:哦…我明白了!
(1)证明AF∥CE;
(2)指出小丽作法中存在的问题.
【点拨】(1)根据小明的作法知,CF=AE,根据平行四边形的性质求出AD∥BC,根据“一组对边平行且相等的四边形是平行四边形”求出四边形AFCE是平行四边形,根据“平行四边形的对边互相平行”即可得证;
(2)以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
【解析】(1)证明:根据小明的作法知,CF=AE,
∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵CF=AE,
∴四边形AFCE是平行四边形,
∴AF∥CE;
(2)解:以A为圆心,EC为半径画弧,交BC于点F,此时可能会有两个交点,只有其中之一符合题意.
故小丽的作法有问题.
【点睛】此题考查了平行四边形的判定与性质,熟记平行四边形的判定定理与性质定理是解题的关键.
22.(2024 西宁)如图,在△ABC中,∠ACB=90°,AC=BC,点D在AC上,过点D作DE∥BC交AB于点E,延长BC到点F,使CF=AD,连接CE,DF.
(1)求证:四边形DFCE是平行四边形.
(2)若∠DCE=30°,AC=2,求FC的长.
【点拨】(1)由等腰直角三角形的性质得∠A=∠B=45°,进而证明∠A=∠AED,得AD=DE,再证明DE=CF,然后由平行四边形的判定即可得出结论;
(2)由平行四边形的性质得FC=DE,设AD=DE=FC=x,则DC=AC﹣AD=2﹣x,再由含30°角的直角三角形的性质得CE=2DE=2x,然后由勾股定理得出方程,解方程即可.
【解析】(1)证明:∵∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
∵DE∥BC,
∴∠ADE=∠ACB=90°,∠AED=∠B=45°,
∴∠A=∠AED,
∴AD=DE,
∵CF=AD,
∴DE=CF,
又∵DE∥FC,
∴四边形DFCE是平行四边形;
(2)解:由(1)可知,四边形DFCE是平行四边形,
∴FC=DE,
设AD=DE=FC=x,则DC=AC﹣AD=2﹣x,
由(1)可知,∠ADE=90°,
∴∠CDE=90°,
在Rt△DEC中,∠DCE=30°,
∴CE=2DE=2x,
由勾股定理得:DE2+CD2=CE2,
即x2+(2﹣x)2=(2x)2,
解得:x=﹣1,x2=﹣﹣1(不符合题意,舍去),
∴FC=﹣1.
【点睛】本题考查了平行四边形的判定与性质、等腰直角三角形的性质、平行线的性质、含30°角的直角三角形的性质以及勾股定理等知识,熟练掌握平行四边形的判定与性质是解题的关键.
23.(2024 北京)如图,在四边形ABCD中,E是AB的中点,DB,CE交于点F,DF=FB,AF∥DC.
(1)求证:四边形AFCD为平行四边形;
(2)若∠EFB=90°,tan∠FEB=3,EF=1,求BC的长.
【点拨】(1)根据三角形中位线定理得到EF∥AD,根据平行四边形的判定定理得到结论;
(2)根据三角形中位线定理求得AD=2EF=2,根据三角函数的定义得到BF=3EF=3,求得DF=BF=3,根据勾股定理得到AF==,根据平行四边形的性质得到CD=AF=,根据线段垂直平分线的性质得到结论.
【解析】(1)证明:∵E是AB的中点,
∴AE=BE,
∵DF=BF,
∴EF是△ABD的中位线,
∴EF∥AD,
∴CF∥AD,
∵AF∥CD,
∴四边形AFCD为平行四边形;
(2)解:由(1)知,EF是△ABD的中位线,
∴AD=2EF=2,
∵∠EFB=90°,tan∠FEB=3,
∴BF=3EF=3,
∵DF=FB,
∴DF=BF=3,
∵AD∥CE,
∴∠ADF=∠EFB=90°,
∴AF==,
∵四边形AFCD为平行四边形,
∴CD=AF=,
∵DF=BF,CE⊥BD,
∴BC=CD=.
【点睛】本题考查了平行四边形的判定和性质,解直角三角形,三角形中位线定理,勾股定理,熟练掌握平行四边形的判定和性质定理是解题的关键.
24.(2024 东城区二模)如图,在四边形ABCD中,点E在BC上,AE∥CD,∠ACB=∠DAC,EF⊥AB于点F,EG⊥AC于点G,EF=EG.
(1)求证:四边形AECD是平行四边形;
(2)若CD=4,∠B=45°,∠CEG=15°,求AB的长.
【点拨】(1)证明AD∥CE,再由平行四边形的判定即可得出结论;
(2)由平行四边形的性质得AE=CD=4,进而证明Rt△AFE≌Rt△AGE(HL),再证明△BEF是等腰直角三角形,然后证明由含30°的直角三角形的性质得BF=EF=2,进而由勾股定理求出AF的长,即可解决问题.
【解析】(1)证明:∵∠ACB=∠DAC,
∴AD∥CE,
∵AE∥CD,
∴四边形AECD是平行四边形;
(2)解:由(1)可知,四边形AECD是平行四边形,
∴AE=CD=4,
∵EF⊥AB,EG⊥AC,
∴∠AFE=∠AGE=90°,
在Rt△AFE和Rt△AGE中,
,
∴Rt△AFE≌Rt△AGE(HL),
∴∠AEF=∠AEG,
∵∠BFE=180°﹣90°=90°,∠B=45°,
∴△BEF是等腰直角三角形,
∴BF=EF,∠BEF=45°,
∴∠FEG=180°﹣∠BEF﹣∠CEG=180°﹣45°﹣15°=120°,
∴∠AEF=∠AEG=∠FEG=60°,
∴∠EAF=90°﹣∠AEF=30°,
∴BF=EF=AE=2,
∴AF===2,
∴AB=AF+BF=2+2.
【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、平行线的判定、含30°角的直角三角形的性质以及勾股定理等知识,熟练掌握平行四边形的判定与性质和全等三角形的判定与性质是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
