阅读与思考:函数概念的发展历程 课件(共19张PPT)-2024-2025学年人教A版(2019)高中数学必修一
文档属性
| 名称 | 阅读与思考:函数概念的发展历程 课件(共19张PPT)-2024-2025学年人教A版(2019)高中数学必修一 |  | |
| 格式 | pptx | ||
| 文件大小 | 29.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 12:33:22 | ||
图片预览





文档简介
(共19张PPT)
阅读与思考
函数概念的发展历程
高中数学>人教A版2019>必修第1册>第三章 函数的概念与性质
学习目标
1.了解函数概念的发展历程,函数概念表述的变化,体会数学概念抽象的层次性。
2.从数学文化的角度,体会函数概念发展的历史原因及在生活生产、社会发展中的作用,感受数学家精神
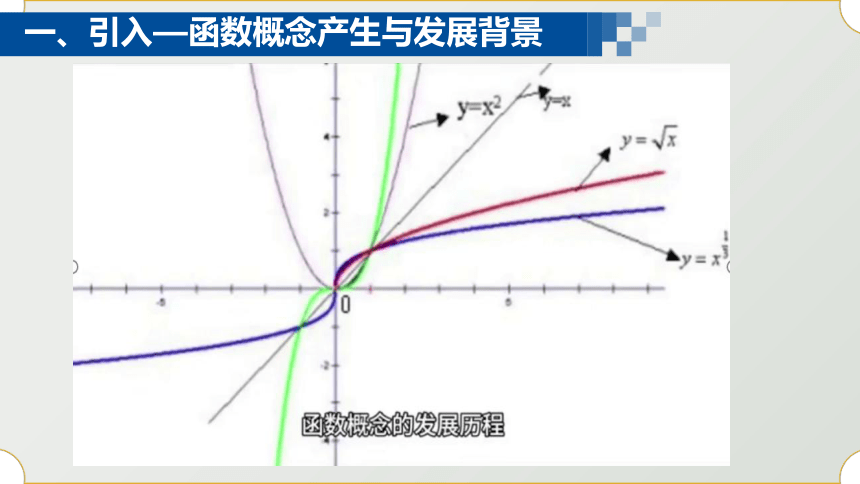
一、引入—函数概念产生与发展背景
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
函数概念经历了哪些发展历程?
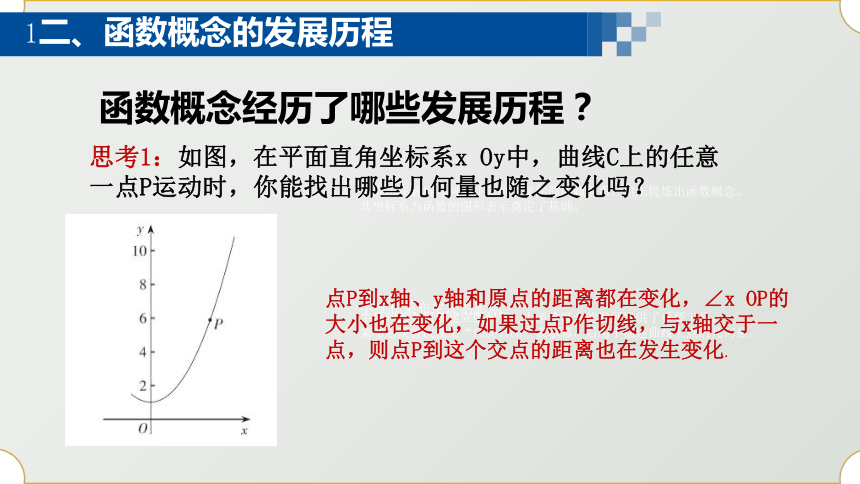
思考1:如图,在平面直角坐标系x Oy中,曲线C上的任意一点P运动时,你能找出哪些几何量也随之变化吗?
点P到x轴、y轴和原点的距离都在变化,∠x OP的大小也在变化,如果过点P作切线,与x轴交于一点,则点P到这个交点的距离也在发生变化.
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
小组交流展示1:课前任务成果(几何观点下的函数)
课前阅读“函数概念的发展历程”材料,并查阅和收集有关函数概念发展历程中各阶段的素材,围绕以下问题,小组合作完成
探究函数概念各发展历程特点及有哪些代表人物、主要成就?
第1阶段:早期函数概念——几何观点下的函数
1二、函数概念的发展历程
第1阶段:早期函数概念——几何观点下的函数
总结:笛卡尔引入变量,用函数表示几何量,函数是函数图象的雏形,今后数形结合思想是我们理解数学概念的重要工具,函数概念体现为一种思想.
思考:应该如何刻画变量之间的关系呢?历史上数学家们在解决微积分问题时也遇到了这个问题,我们一起来看一下他们是怎么解决的
笛卡尔
牛顿和莱布尼茨的影响
1二、函数概念的发展历程
第2阶段:十八世纪函数概念——代数观点下的函数
小组交流展示2:课前任务成果(代数观点)
总结:通过代数式表达变量关系,完成从几何图形的理解到代数式表达的过程
讨论:对于这种表示方法的优缺点,谈一谈你的认识?
欧拉
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
1二、函数概念的发展历程
思考2:所有的函数都有解析式吗?
背景:18世纪中期,数学家们一直在争论振动弦问题,即拨动一根两端固定的弹性弦,使其具有某种初始形状,然后将其释放出来振动.如何用函数描述某一时刻弦的形状?数学家们对任意一段曲线是否有函数解析式展开了讨论,从而推进了函数概念的发展
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
柯西
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
总结:函数不一定能用函数解析式来表达,只要两个变量之间有依赖关系,那就是函数,反映了函数概念中蕴含的辩证思想,体现了从自变到因变的过程
背景:1829年,德国数学家狄利克雷因为傅里叶级数创造了一个新函数:
这个函数用“变量依赖”定义如何解释呢?图象呢?
狄利克雷
思考3:所有的函数都有函数图象吗?
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
第3阶段:十九世纪函数概念—对应关系下的函数
小组交流展示3:课前任务成果(对应关系)
黎曼
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
总结:函数对应说摆脱了变量依赖的束缚,将函数概念置于这一更加一般的框架之中,较清楚地说明了函数的内涵,使函数的适用范围更广泛.
黎曼
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
1二、函数概念的发展历程
第4阶段:现代函数概念—集合论下的函数
小组交流展示4:课前任务成果(现代函数)
格奥尔格·康托尔
背景:1874年——康托尔开创了集合论,到20世纪初,集合论的思想渗透到数学各个领域并且现代数学的各个分支几乎所有成果都构筑在严格的集合理论上。
1900年的国际数学家大会上,法国著名数学家庞加莱就非常兴奋地称:借助集合论概念,我们可以建造整个数学大厦
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
第4阶段:现代函数概念—集合论下的函数
维布伦
库拉托夫斯基
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
二、函数概念的发展历程
总结:从变量对应到集合对应,将函数概念置于集合映射、序偶,这一更加一般的框架之中,摆脱了变量的束缚,使函数的适用范围更广泛.集合对应就是我们高中学习的.
三、以史为鉴,理解函数概念
思考与感悟:从数学史的角度来看,初中阶段和高中阶段对函数概念的定义有什么不同?
初中:
高中:
四、课堂小结
通过本节学习,你收获了什么?谈一下你的感受吧!
(知识方面或研究方法方面或者对数学家、数学文化方面的体会、感想)
17世纪“几何起源”
19世纪“对应观点”
18世纪“代数观点”
现代函数“集合论”
勤于思考
敢于探索
勇于创新
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
五、布置作业
作业1:以时间轴、图表或思维导图的形式整理函数概念的发展历程.
作业2:通过查阅书籍、上网等方式搜集素材,进一步了解函数概念的
发展历程,选择自己感兴趣的一个主题形成数学小论文,在班
里交流讨论.
(参考选题:函数产生的社会背景;函数符号的故事;数学家与函数)
感谢观看
阅读与思考
函数概念的发展历程
高中数学>人教A版2019>必修第1册>第三章 函数的概念与性质
学习目标
1.了解函数概念的发展历程,函数概念表述的变化,体会数学概念抽象的层次性。
2.从数学文化的角度,体会函数概念发展的历史原因及在生活生产、社会发展中的作用,感受数学家精神
一、引入—函数概念产生与发展背景
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
函数概念经历了哪些发展历程?
思考1:如图,在平面直角坐标系x Oy中,曲线C上的任意一点P运动时,你能找出哪些几何量也随之变化吗?
点P到x轴、y轴和原点的距离都在变化,∠x OP的大小也在变化,如果过点P作切线,与x轴交于一点,则点P到这个交点的距离也在发生变化.
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
小组交流展示1:课前任务成果(几何观点下的函数)
课前阅读“函数概念的发展历程”材料,并查阅和收集有关函数概念发展历程中各阶段的素材,围绕以下问题,小组合作完成
探究函数概念各发展历程特点及有哪些代表人物、主要成就?
第1阶段:早期函数概念——几何观点下的函数
1二、函数概念的发展历程
第1阶段:早期函数概念——几何观点下的函数
总结:笛卡尔引入变量,用函数表示几何量,函数是函数图象的雏形,今后数形结合思想是我们理解数学概念的重要工具,函数概念体现为一种思想.
思考:应该如何刻画变量之间的关系呢?历史上数学家们在解决微积分问题时也遇到了这个问题,我们一起来看一下他们是怎么解决的
笛卡尔
牛顿和莱布尼茨的影响
1二、函数概念的发展历程
第2阶段:十八世纪函数概念——代数观点下的函数
小组交流展示2:课前任务成果(代数观点)
总结:通过代数式表达变量关系,完成从几何图形的理解到代数式表达的过程
讨论:对于这种表示方法的优缺点,谈一谈你的认识?
欧拉
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
1二、函数概念的发展历程
思考2:所有的函数都有解析式吗?
背景:18世纪中期,数学家们一直在争论振动弦问题,即拨动一根两端固定的弹性弦,使其具有某种初始形状,然后将其释放出来振动.如何用函数描述某一时刻弦的形状?数学家们对任意一段曲线是否有函数解析式展开了讨论,从而推进了函数概念的发展
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
柯西
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
总结:函数不一定能用函数解析式来表达,只要两个变量之间有依赖关系,那就是函数,反映了函数概念中蕴含的辩证思想,体现了从自变到因变的过程
背景:1829年,德国数学家狄利克雷因为傅里叶级数创造了一个新函数:
这个函数用“变量依赖”定义如何解释呢?图象呢?
狄利克雷
思考3:所有的函数都有函数图象吗?
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
第3阶段:十九世纪函数概念—对应关系下的函数
小组交流展示3:课前任务成果(对应关系)
黎曼
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
总结:函数对应说摆脱了变量依赖的束缚,将函数概念置于这一更加一般的框架之中,较清楚地说明了函数的内涵,使函数的适用范围更广泛.
黎曼
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
1二、函数概念的发展历程
第4阶段:现代函数概念—集合论下的函数
小组交流展示4:课前任务成果(现代函数)
格奥尔格·康托尔
背景:1874年——康托尔开创了集合论,到20世纪初,集合论的思想渗透到数学各个领域并且现代数学的各个分支几乎所有成果都构筑在严格的集合理论上。
1900年的国际数学家大会上,法国著名数学家庞加莱就非常兴奋地称:借助集合论概念,我们可以建造整个数学大厦
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
1二、函数概念的发展历程
第4阶段:现代函数概念—集合论下的函数
维布伦
库拉托夫斯基
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
二、函数概念的发展历程
总结:从变量对应到集合对应,将函数概念置于集合映射、序偶,这一更加一般的框架之中,摆脱了变量的束缚,使函数的适用范围更广泛.集合对应就是我们高中学习的.
三、以史为鉴,理解函数概念
思考与感悟:从数学史的角度来看,初中阶段和高中阶段对函数概念的定义有什么不同?
初中:
高中:
四、课堂小结
通过本节学习,你收获了什么?谈一下你的感受吧!
(知识方面或研究方法方面或者对数学家、数学文化方面的体会、感想)
17世纪“几何起源”
19世纪“对应观点”
18世纪“代数观点”
现代函数“集合论”
勤于思考
敢于探索
勇于创新
笛卡尔在解析几何中注意到变量间的依赖关系,但未提炼出函数概念。
其坐标系为函数的图形表示奠定了基础。
牛顿和莱布尼茨的影响
牛顿和莱布尼茨建立微积分,为函数概念的发展提供了重要工具。
莱布尼茨首次使用“function”表示幂,后用于描述曲线上点的几何量。
五、布置作业
作业1:以时间轴、图表或思维导图的形式整理函数概念的发展历程.
作业2:通过查阅书籍、上网等方式搜集素材,进一步了解函数概念的
发展历程,选择自己感兴趣的一个主题形成数学小论文,在班
里交流讨论.
(参考选题:函数产生的社会背景;函数符号的故事;数学家与函数)
感谢观看
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
