苏科版七年级数学下册第九章单元练习(无答案)
文档属性
| 名称 | 苏科版七年级数学下册第九章单元练习(无答案) | 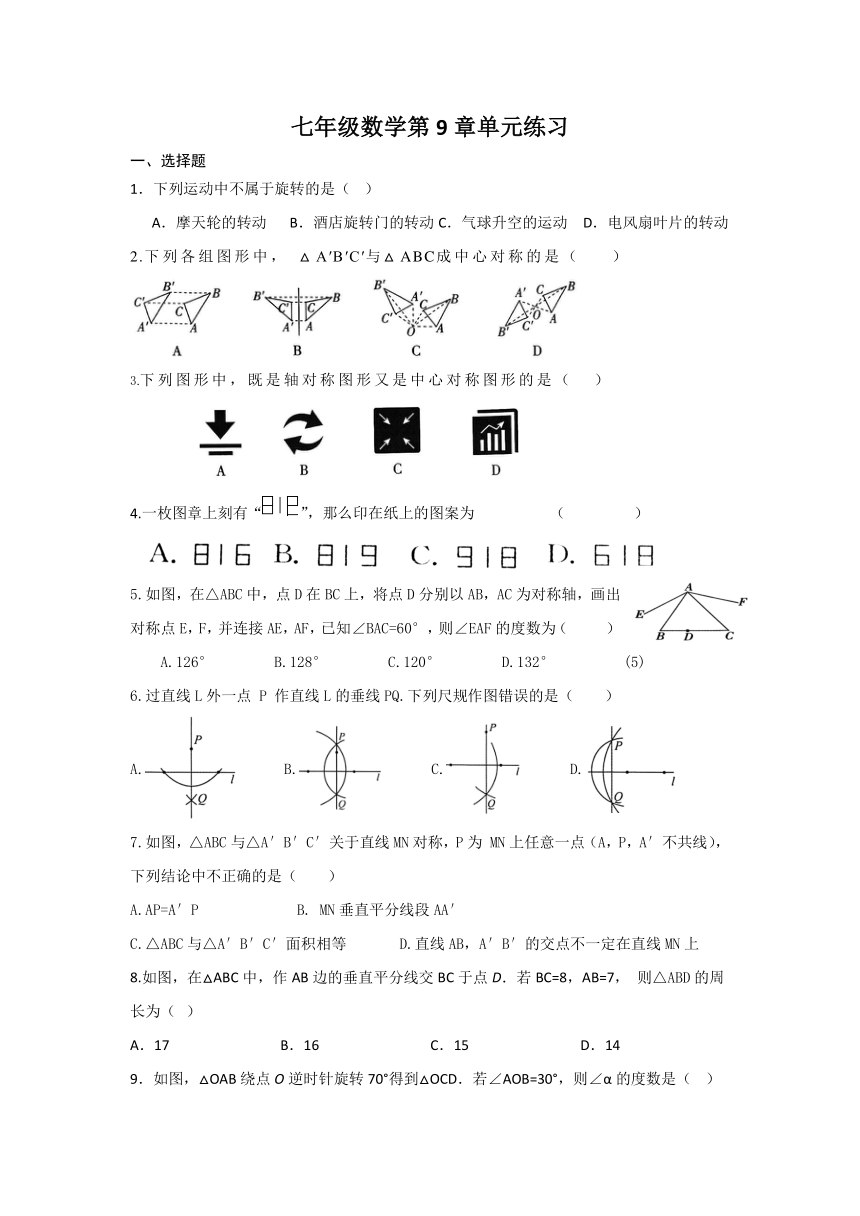 | |
| 格式 | docx | ||
| 文件大小 | 521.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-01 09:49:26 | ||
图片预览


文档简介
七年级数学第9章单元练习
选择题
1.下列运动中不属于旋转的是( )
A.摩天轮的转动 B.酒店旋转门的转动C.气球升空的运动 D.电风扇叶片的转动
2.下列各组图形中, △A′B′C′与△ABC成中心对称的是( )
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
4.一枚图章上刻有“”,那么印在纸上的图案为 ( )
5.如图,在△ABC中,点D在BC上,将点D分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF,已知∠BAC=60°,则∠EAF的度数为( )
A.126° B.128° C.120° D.132° (5)
6.过直线L外一点 P 作直线L的垂线PQ.下列尺规作图错误的是( )
A. B. C. D.
7.如图,△ABC与△A′B′C′关于直线MN对称,P为 MN上任意一点(A,P,A′不共线),下列结论中不正确的是( )
A.AP=A′P B. MN垂直平分线段AA′
C.△ABC与△A′B′C′面积相等 D.直线AB,A′B′的交点不一定在直线MN上
8.如图,在△ABC中,作AB边的垂直平分线交BC于点D.若BC=8,AB=7, 则△ABD的周长为( )
A.17 B.16 C.15 D.14
9.如图,△OAB绕点O逆时针旋转70°得到△OCD.若∠AOB=30°,则∠α的度数是( )
A.30° B.40° C.50° D.60°
(8) (9)
10.如图,将三角形平移得到三角形,下列结论中,不一定成立的是( )
A.或与在同一条直线上
B.或与在同一条直线上
C.
D.
11.如图,正方形网格中的每个小正方形的边长为1,将△ABC绕旋转中心旋转某个角度后得到△A′B′C′,其中点A,B,C的对应点分别是点A′,B′,C′,那么旋转中心是( )
A.点Q B.点P C.点N D.点M
12.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C' 的位置,使得 CC′ //AB,则∠BAB′ 的度数是( )
A.30° B.35° C.40° D.50°
(12)
二.填空题
1.如图,△ABC与关于直线对称,∠F=30°,∠A=55°,则的度数为
2.如图,△ABC经过平移得到,连接,若BB,=5cm则点A与点之间的距离为
3.如图,△ABC,,∠BAC=35°.将△ABC绕点逆时针旋转得,使点的对应点恰好落在边上,则的度数是 °.
4.如图,△ABD和△ACD关于直线AD对称,点E,F是线段AD上的任意两点,若△ABC的面积为18cm2,则图中阴影部分的面积是 cm2.
5.如图,把△ABC绕点A逆时针旋转得到△ADE,点B,C的对应点分别是点D,E,且点E在BC的延长线上,连接BD,则下列结论一定正确的是( )
A.∠CAE=∠BED B.AB=AE C.∠ACE=∠ADE D.CE=BD
6.如图,直线a,b垂直相交于点O,曲线c关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为______.
(2) (3)
(5) (6)
如图,在长方形中,在上分别截取,使,分别以E、F为圆心、以大于长为半径作弧,两弧在内交于点G,作射线;又分别以A、C为圆心,以大于长为半径作弧,两弧相交于点M和N,作直线;射线和直线交于点P,则的度数为 ______.°
三.作图题
1.相关部门要在如图所示的一条笔直的路边 l 建一个燃气站,向 l 同侧的A,B两个城镇分别铺设管道输送燃气.试确定燃气站的位置,使铺设管道的路线最短.(保留画图痕迹,辅助线用虚线,最短路径)
. .
.
2.如图,已知△ABC和直线l,点C在l上.用直尺和圆规作△ABC关于直线 l 对称的三角形.
3.如图,已知△ABC和△EFD成中心对称, 在图中画出其对称中心O
(3)
4.把长方形ABCD(如图)沿箭头所指的方向平移,使点C落在点C'。画出经这一平移后所得的图形。
四.解答题
1.如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把进行平移,得到,使点A与对应,请在网格中画出;
(2)连接AA',BB',则线段AA',BB之间的关系是
(3)的面积为 .
2.如图所示,由每一个边长均为1的小正方形构成的8×8正方形网格中,点A,B,C,M,N均在格点上(小正方形的顶点为格点),利用网格画图.
(1)画出△ABC关于直线MN对称的△A'B'C';
(2)在线段MN上找一点P,使得线段PA+PC最小(保留必要的画图痕迹,并标出点P位置)
(3)连接,,求四边形的面积;
选择题
1.下列运动中不属于旋转的是( )
A.摩天轮的转动 B.酒店旋转门的转动C.气球升空的运动 D.电风扇叶片的转动
2.下列各组图形中, △A′B′C′与△ABC成中心对称的是( )
3.下列图形中,既是轴对称图形又是中心对称图形的是( )
4.一枚图章上刻有“”,那么印在纸上的图案为 ( )
5.如图,在△ABC中,点D在BC上,将点D分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF,已知∠BAC=60°,则∠EAF的度数为( )
A.126° B.128° C.120° D.132° (5)
6.过直线L外一点 P 作直线L的垂线PQ.下列尺规作图错误的是( )
A. B. C. D.
7.如图,△ABC与△A′B′C′关于直线MN对称,P为 MN上任意一点(A,P,A′不共线),下列结论中不正确的是( )
A.AP=A′P B. MN垂直平分线段AA′
C.△ABC与△A′B′C′面积相等 D.直线AB,A′B′的交点不一定在直线MN上
8.如图,在△ABC中,作AB边的垂直平分线交BC于点D.若BC=8,AB=7, 则△ABD的周长为( )
A.17 B.16 C.15 D.14
9.如图,△OAB绕点O逆时针旋转70°得到△OCD.若∠AOB=30°,则∠α的度数是( )
A.30° B.40° C.50° D.60°
(8) (9)
10.如图,将三角形平移得到三角形,下列结论中,不一定成立的是( )
A.或与在同一条直线上
B.或与在同一条直线上
C.
D.
11.如图,正方形网格中的每个小正方形的边长为1,将△ABC绕旋转中心旋转某个角度后得到△A′B′C′,其中点A,B,C的对应点分别是点A′,B′,C′,那么旋转中心是( )
A.点Q B.点P C.点N D.点M
12.如图,在△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C' 的位置,使得 CC′ //AB,则∠BAB′ 的度数是( )
A.30° B.35° C.40° D.50°
(12)
二.填空题
1.如图,△ABC与关于直线对称,∠F=30°,∠A=55°,则的度数为
2.如图,△ABC经过平移得到,连接,若BB,=5cm则点A与点之间的距离为
3.如图,△ABC,,∠BAC=35°.将△ABC绕点逆时针旋转得,使点的对应点恰好落在边上,则的度数是 °.
4.如图,△ABD和△ACD关于直线AD对称,点E,F是线段AD上的任意两点,若△ABC的面积为18cm2,则图中阴影部分的面积是 cm2.
5.如图,把△ABC绕点A逆时针旋转得到△ADE,点B,C的对应点分别是点D,E,且点E在BC的延长线上,连接BD,则下列结论一定正确的是( )
A.∠CAE=∠BED B.AB=AE C.∠ACE=∠ADE D.CE=BD
6.如图,直线a,b垂直相交于点O,曲线c关于点O成中心对称,点A的对称点是点A′,AB⊥a于点B,A′D⊥b于点D.若OB=3,OD=2,则阴影部分的面积之和为______.
(2) (3)
(5) (6)
如图,在长方形中,在上分别截取,使,分别以E、F为圆心、以大于长为半径作弧,两弧在内交于点G,作射线;又分别以A、C为圆心,以大于长为半径作弧,两弧相交于点M和N,作直线;射线和直线交于点P,则的度数为 ______.°
三.作图题
1.相关部门要在如图所示的一条笔直的路边 l 建一个燃气站,向 l 同侧的A,B两个城镇分别铺设管道输送燃气.试确定燃气站的位置,使铺设管道的路线最短.(保留画图痕迹,辅助线用虚线,最短路径)
. .
.
2.如图,已知△ABC和直线l,点C在l上.用直尺和圆规作△ABC关于直线 l 对称的三角形.
3.如图,已知△ABC和△EFD成中心对称, 在图中画出其对称中心O
(3)
4.把长方形ABCD(如图)沿箭头所指的方向平移,使点C落在点C'。画出经这一平移后所得的图形。
四.解答题
1.如图,在边长为1个单位长度的小正方形组成的网格中.
(1)把进行平移,得到,使点A与对应,请在网格中画出;
(2)连接AA',BB',则线段AA',BB之间的关系是
(3)的面积为 .
2.如图所示,由每一个边长均为1的小正方形构成的8×8正方形网格中,点A,B,C,M,N均在格点上(小正方形的顶点为格点),利用网格画图.
(1)画出△ABC关于直线MN对称的△A'B'C';
(2)在线段MN上找一点P,使得线段PA+PC最小(保留必要的画图痕迹,并标出点P位置)
(3)连接,,求四边形的面积;
同课章节目录
