【核心考点集训】第一单元《小数的意义和加减法》课件(共34张PPT)--北师大版四年级下册
文档属性
| 名称 | 【核心考点集训】第一单元《小数的意义和加减法》课件(共34张PPT)--北师大版四年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 30.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
北师大版 数学 四年级 下册
小数的意义和加减法
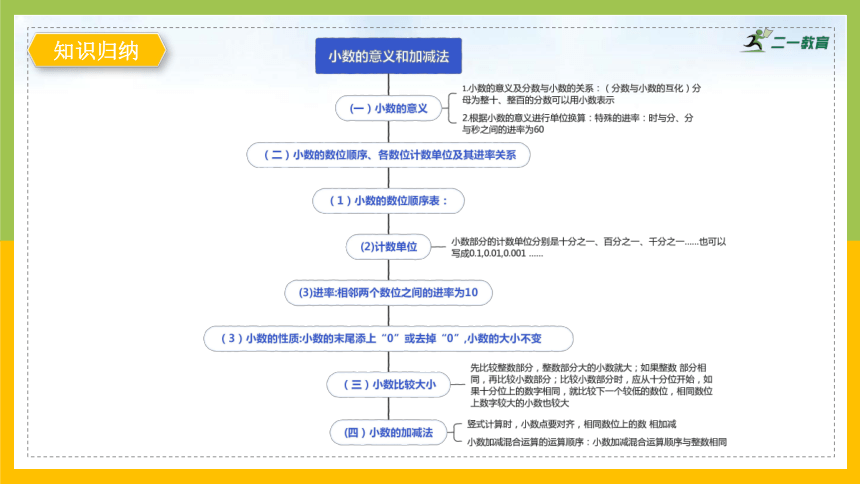
知识归纳
模块一:知识点复习
1、把单位“1”平均分成 10 份、100 份、1000 份……取其中的 1 份或几份,表示十分之几、百分之几、千份之几……的数,叫小数。
2、分母是 10、100、1000……的分数可以用小数表示表示十分之几的小数是一位小数;表示百分之几的小数是两位小数;表示千分之几的小数是三位小数……
知识点一:小数的意义
知识梳理
3、小数的数位、计算单位、进率:
①小数的计数单位是十分之一、百分之一、千分之一……分别写作 0.1、 0.01、0.001……与整数一样,小数每相邻两个计数单位之间的进率是 10。
②小数部分最大的计算单位是十分之一,小数部分没有最小的计数单位。
③小数的数位是无限的。
④在一个小数中,小数点后面含有几个小数数位,它就是几位小数。小数部分末尾的零也要计入其中。
知识点一:小数的意义
知识点一:小数的意义
整数部分 小 数 点 小数部分
数位 ...... 千 位 百 位 十 位 个 位 十 分 位 百 分 位 千 分 位 万 分 位 .......
计数单位 ...... 千 百 十 个 (一) 十 分 之 一 百 分 之 一 千 分 之 一 万 分 之 一 ......
4、小数数位顺序表
知识点二:小数的读写
1.读小数时,从左往右,整数部分按照整数的读法来读(整数部分是 0的读作“零”),小数点读作“点”,小数部分顺次读出每一个数位上的数字,即使是连续的 0,也要依次读出来。
2.写小数时,也是从左往右,整数部分按照整数的写法来写(整数部分是零的写作“0”),小数点点在个位的右下角,小数部分顺次写出每一个数位上的数字。
知识点三:单位换算
①低级单位单名数化为高级单位时,先将这个低级单位的数改写成分母是 10、100、1000……的分数,再把分数写成小数的形式,并在后面加上所要化成的高级单位的名称。
②复名数改单名数:抄相同,改不同。(相同的单位抄在整数部分,不相同的单位按照上面的改写方法写在小数部分)。
知识点三:单位换算
③其他改写方法:
单名数互化:
低级单位名数÷进率=高级单位名数。
高级单位名数×进率=低级单位名数。
复名数与单名数之间互化:抄相同,改不同(同单名数互化方法)
如:3 米 2 厘米=(3.02)米。
相同的单位米,抄在整数部分,整数部分是3;
改写不同:2 厘米÷100=0.02 米
知识点四:比大小
①比较两个小数大小的方法:先看整数部分,整数部分大的小数就大;整数部分相同,再看小数部分的十分位,十分位上数字大的小数就大……
②把几个小数按顺序排列:要先比较它们的大小,再按照题目的要求按顺序排列。当单位不统一的几个数量比较大小时,要先将这几个数量的单位统一,再按小数大小比较方法进行比较,最后答题应按照最目中给的原数进行排列顺序。
知识点五:小数加、减法的意义
小数加减法的意义与整数加减法的意义相同。
①小数加法的意义:把两个数合并成一个数的运算
②小数减法的意义:已知两个加数的和与其中的一个加数,求另一个 加数的运算。
知识点六:小数加减计算法则与小数加减混合运算
小数点对齐;按照整数加减法的法则计算。从末位算起;哪一位上的数相加满十,要向前一位进一。如果被减数的小数末尾位数不够,可以添“0”再减,哪一位上的数不够减,要从前一位退一,在本位上加十再减;得数的小数点要对齐横线上的小数点。
①和整数加减混合运算的顺序相同。同级运算,从左往右;有括号的,先里后外。
②整数加、减法的运算定律同样适用于小数加减法。例如加法的结合律,交换律。
模块二:例题讲解
【典例1】组数问题(列举法)
用分别写有1,5,8和小数点的四张卡片组数,你能组成哪些两位小数 请把它们都写出来。(卡片全用上且不重复使用)
因为要组成两位小数,所以整数部分是一位数,小数部分是两位数。
以1为整数部分时,可组成1.58和1.85;
以5为整数部分时,可组成5.18和5.81;
以8为整数部分时,可组成8.15和8.51。
总结:能组成的两位小数有1.58、1.85、5.18.、5.81、8.15、8.51。
甲、乙、丙、丁四人的体重分别是36.8千克、45.6千克、37.2千克、42千克中的一个。已知甲比丁重,但比丙轻,丁比乙轻,甲比乙重。甲、乙、丙、丁四人的体重各是多少千克
【典例2】比较小数大小(推理法)
首先:梳理体重关系:已知甲比丁重,但比丙轻,可表示为丙>甲>丁;又因为丁比乙轻,甲比乙重,即甲>乙>丁。综合可得:丙>甲>乙>丁。
最后得出答案:甲的体重是42千克,乙的体重是37.2千克丙的体重是45.6千克,丁的体重是36.8千克。
其次:对应体重数值:在36.8千克、45.6千克、37.2千克、42千克中,从大到小排序为45.6千克>42千克>37.2千克>36.8千克。所以丙的体重是45.6千克,甲的体重是42千克,乙的体重是37.2千克,丁的体重是36.8千克。
一个两位小数,最高位十位上的数是9,个位上的数是最小的自然数,十分位上的数表示6个,十分位上的数是百分位上的数的3倍。这个两位小数是( )。
【典例3】用小数的数位知识猜数
首先:确定各数位数字:已知最高位十位上的数是9;个位上的数是最小的自然数,即0;十分位上的数表示6个0.1,所以十分位上的数是6;又因为十分位上的数是百分位上的数的3倍,所以百分位上的数是6÷3=2。
再写出这个两位小数按照数位顺序,这个两位小数是90.62
90.62
【典例4】错中求解问题
淘气在计算一道加法算式时,错把3.2看成了32,算得的结果是55.7。这道题正确的结果是多少
首先:求出另一个加数因为错把3.2看成了32,算得的结果是55.7,所以另一个加数为:55.7-32=23.7。
再计算正确结果用求出的加数加上正确的3.2
正确结果为:55.7-32=23.7 23.7+3.2=26.9。
【典例5】小数加减法中和或差的变化规律
两个数的和是73.6,如果其中一个加数增加11.52,另一个加数减少8.34,那么和变成了多少
分析和的变化:一个加数增加11.52,和会增加11.52;另一个加数减少8.34,和会减少8.34。
计算变化后的和:原来两数的和是73.6
变化后的和为:73.6+11.52-8.34=76.78
【典例6】和差问题
妈妈从菜市场买回7.2千克青椒和土豆,已知青椒比土豆少2.8千克。青椒和土豆各有多少千克
图:
列式:
求土豆的重量:(7.2+2.8)÷2=5(kg)
求青椒的重量:7.2-5=2.2(kg)
【典例7】小数加减法的实际问题(画图法)
淘气家到学校的距离大约是1.8千米。这天淘气放学时向家走了0.6千米后,发现忘记带数学课本了,于是他立即原路返回取数学课本,再回家。这天放学,淘气一共走了多少千米
图:
列式:
淘气多走的路程为:0.6×2=1.2千米
淘气放学一共走的路程为:
1.8+1.2=3(千米)
【典例8】小数加减法的实际问题(消元法)
丁丁、阳阳、欣欣共有零花钱99.6元,其中丁丁、阳阳共有71.2元,丁丁、欣欣共有38.5元。丁丁有多少零花钱
方法一:
列式:
71.2+38.5-109.7(元)
109.7-99.6=10.1(元)
【典例8】小数加减法的实际问题(消元法)
丁丁、阳阳、欣欣共有零花钱99.6元,其中丁丁、阳阳共有71.2元,丁丁、欣欣共有38.5元。丁丁有多少零花钱
方法二:
列式:
99.6-71.2=28.4(元)
38.5-28.4=10.1(元)
【典例9】简便运算
找基准数法
0.9+0.99+0.999+0.9999
分析:
把0.9看成1-0.1,
0.99看成1-0.01;
0.999看成1-0.001;
0.9999看成1-0.0001。
0.9+0.99+0.999+0.9999
=(1-0.1)+(1-0.01)+(1-0.001)+(1-0.0001)
=(1+1+1+1)-(0.1+0.01+0.001+0.0001)
=4-0.1111
=3.8889
【典例9】简便运算
【典例9】简便运算
配对求和法
0.1+0.2+0.3+…+0.8+0.9
分析:
0.1和0.9配对相加得0.1+0.9=1,
0.2和0.8配对相加得0.2+0.8=1,
0.3和0.7配对相加得0.3+0.7=1,
0.4和0.6配对相加得0.4+0.6=1,
还剩下0.5。
一共有4对和为1的数,再加上0.5。
【典例9】简便运算
0.1+0.2+0.3+…+0.8+0.9
=(0.1+0.9)+(0.2+0.8)+(0.3+0.7)+(0.4+0.6)+0.5
=1×4+0.5
=4.5
模块三:完成变式训练
1.用1,3,0,7这四个数字和小数点写出含有0,但(不读出来的两位小数(每个数字只能用一次),至少写4个。
10.37 11.17 12.13 13.73 答案不唯一
2.森林运动会上,小动物们进行50米赛跑。赛跑成绩分别是8.9秒、9.3秒、8.6秒和9.9秒。它们的赛跑成绩分别是多少秒
它们的赛跑成绩分别是:
小免8.6秒,小狗8.9秒,小猫9.3秒,小猴9.9秒。
3.(1)□□□是一个三位小数,十分位上的数是千分位上的数的2倍,百分位上的数是十分位上的数的4倍,并且小数部分的数都不是0。这个三位小数是( )。
0.281
(2)ab.cd是一个两位小数,a,b,c,d分别代表0,3,6,9中的某一个数字。满足ad>b且小数)。末尾不为零的两位小数有( )。
30.96或60.93
4.(1)丁丁在计算一道减法题时,错误地把减数3.6看成了6.3,计算出结果是0.27。这道题正确的结果是多少
先根据错误的减数和结果求出被减数,被减数为6.3+0.27=6.57
再用被减数减去正确的减数,得到正确结果为6.57-3.6=2.97。
(2)小凯在计算4.25加一个一位小数时,由于他只把数的末尾对齐,结果得到6.28。正确的得数是多少
先根据错误的计算结果和一个加数求出错误的另一个加数,6.28-4.25 =2.03.
因为是一位小数,所以正确的加数是20.3 。
那么正确的得数是4.25 +20.3 =24.55。
5.(1)两个数的和是23.8,如果其中一个加数增加7.2,那么另一个加数怎么变化,和才能比原来少4.5
求加数的变化情况一个加数增加7.2,若和不变,另一个加数应减少7.2。
现在和要比原来少4.5,所以另一个加数还要再减少4.5。
总共另一个加数要减少7.2+4.5 =11.7。
(2)在一道减法算式中,差是16.6,当被减数增加3.5,而减数减少6.8时,差是多少
被减数增加3.5,差会增加3.5;减数减少6.8,差会增加6.8。
差是166+3.5+6.8=26.9 。
6.(1)笑笑买了《趣味数独》和《小学生作文》这两本书,一共花了32.65元,《趣味数独》比《小学生作文》便宜4.65元。这两本书分别是多少元
先算出《小学生作文》价格的2倍:32.65+4.65=37.3(元)
那么《小学生作文》的价格是:37.3-2-18.65(元)
《趣味数独》的价格是:18.65-4.65=14(元)
(2)两筐苹果一共重118.76千克,如果从甲筐中拿出9.38千克苹果放入乙筐,两筐苹果就一样重。甲、乙两筐苹果分别重多少千克
两筐苹果一样重时每筐重118.76-2=59.38(千克)
甲筐原来重59.38+9.38=68.76(千克)
乙筐原来重59.38-9.38=50(千克)
7.刘叔叔拉了一车蔬菜到菜市场售卖,进入菜市场时过地磅称重,连车一起重4.5吨,到中午刚好卖了一半蔬菜,这时连车一起重2.8吨。剩下蔬菜的质量是多少 空车的质量是多少
一半蔬菜的质量是4.5-2.8=1.7(吨)
剩下蔬菜的质量等于一半蔬菜的质量,即1.7吨。
空车的质量是2.8-1.7=1.1(吨)
8.用简便方法计算
4.04+3.97+3.99+4.02 10.02+10.1+9.88+9.75
=(4.04+3.97)+(3.99 +4.02)
=8.01+8.01
=8×2+0.01×2
=16+0.02
=16.02
=(10.02+9.88)+(10.1+9.75)
=19.9+19.85
=(20-0.1)+(20-0.15)
=20+20-(0.1+0.15)
=40-0.25
=39.75
1.2+1.4+1.6+1.8+…+3.6+3.8 0.1+0.3+0.5+…+9.7+9.9。
首先求项数:n=(3.8-1.2)÷0.2+1=14
原式=14 ×(1.2+3.8)÷2
=7×5
=35
项数n=(9.9-0.1)÷0.2+1=50
原式=50×(0.1+ 9.9)÷42
=25×10
=250
北师大版 数学 四年级 下册
小数的意义和加减法
知识归纳
模块一:知识点复习
1、把单位“1”平均分成 10 份、100 份、1000 份……取其中的 1 份或几份,表示十分之几、百分之几、千份之几……的数,叫小数。
2、分母是 10、100、1000……的分数可以用小数表示表示十分之几的小数是一位小数;表示百分之几的小数是两位小数;表示千分之几的小数是三位小数……
知识点一:小数的意义
知识梳理
3、小数的数位、计算单位、进率:
①小数的计数单位是十分之一、百分之一、千分之一……分别写作 0.1、 0.01、0.001……与整数一样,小数每相邻两个计数单位之间的进率是 10。
②小数部分最大的计算单位是十分之一,小数部分没有最小的计数单位。
③小数的数位是无限的。
④在一个小数中,小数点后面含有几个小数数位,它就是几位小数。小数部分末尾的零也要计入其中。
知识点一:小数的意义
知识点一:小数的意义
整数部分 小 数 点 小数部分
数位 ...... 千 位 百 位 十 位 个 位 十 分 位 百 分 位 千 分 位 万 分 位 .......
计数单位 ...... 千 百 十 个 (一) 十 分 之 一 百 分 之 一 千 分 之 一 万 分 之 一 ......
4、小数数位顺序表
知识点二:小数的读写
1.读小数时,从左往右,整数部分按照整数的读法来读(整数部分是 0的读作“零”),小数点读作“点”,小数部分顺次读出每一个数位上的数字,即使是连续的 0,也要依次读出来。
2.写小数时,也是从左往右,整数部分按照整数的写法来写(整数部分是零的写作“0”),小数点点在个位的右下角,小数部分顺次写出每一个数位上的数字。
知识点三:单位换算
①低级单位单名数化为高级单位时,先将这个低级单位的数改写成分母是 10、100、1000……的分数,再把分数写成小数的形式,并在后面加上所要化成的高级单位的名称。
②复名数改单名数:抄相同,改不同。(相同的单位抄在整数部分,不相同的单位按照上面的改写方法写在小数部分)。
知识点三:单位换算
③其他改写方法:
单名数互化:
低级单位名数÷进率=高级单位名数。
高级单位名数×进率=低级单位名数。
复名数与单名数之间互化:抄相同,改不同(同单名数互化方法)
如:3 米 2 厘米=(3.02)米。
相同的单位米,抄在整数部分,整数部分是3;
改写不同:2 厘米÷100=0.02 米
知识点四:比大小
①比较两个小数大小的方法:先看整数部分,整数部分大的小数就大;整数部分相同,再看小数部分的十分位,十分位上数字大的小数就大……
②把几个小数按顺序排列:要先比较它们的大小,再按照题目的要求按顺序排列。当单位不统一的几个数量比较大小时,要先将这几个数量的单位统一,再按小数大小比较方法进行比较,最后答题应按照最目中给的原数进行排列顺序。
知识点五:小数加、减法的意义
小数加减法的意义与整数加减法的意义相同。
①小数加法的意义:把两个数合并成一个数的运算
②小数减法的意义:已知两个加数的和与其中的一个加数,求另一个 加数的运算。
知识点六:小数加减计算法则与小数加减混合运算
小数点对齐;按照整数加减法的法则计算。从末位算起;哪一位上的数相加满十,要向前一位进一。如果被减数的小数末尾位数不够,可以添“0”再减,哪一位上的数不够减,要从前一位退一,在本位上加十再减;得数的小数点要对齐横线上的小数点。
①和整数加减混合运算的顺序相同。同级运算,从左往右;有括号的,先里后外。
②整数加、减法的运算定律同样适用于小数加减法。例如加法的结合律,交换律。
模块二:例题讲解
【典例1】组数问题(列举法)
用分别写有1,5,8和小数点的四张卡片组数,你能组成哪些两位小数 请把它们都写出来。(卡片全用上且不重复使用)
因为要组成两位小数,所以整数部分是一位数,小数部分是两位数。
以1为整数部分时,可组成1.58和1.85;
以5为整数部分时,可组成5.18和5.81;
以8为整数部分时,可组成8.15和8.51。
总结:能组成的两位小数有1.58、1.85、5.18.、5.81、8.15、8.51。
甲、乙、丙、丁四人的体重分别是36.8千克、45.6千克、37.2千克、42千克中的一个。已知甲比丁重,但比丙轻,丁比乙轻,甲比乙重。甲、乙、丙、丁四人的体重各是多少千克
【典例2】比较小数大小(推理法)
首先:梳理体重关系:已知甲比丁重,但比丙轻,可表示为丙>甲>丁;又因为丁比乙轻,甲比乙重,即甲>乙>丁。综合可得:丙>甲>乙>丁。
最后得出答案:甲的体重是42千克,乙的体重是37.2千克丙的体重是45.6千克,丁的体重是36.8千克。
其次:对应体重数值:在36.8千克、45.6千克、37.2千克、42千克中,从大到小排序为45.6千克>42千克>37.2千克>36.8千克。所以丙的体重是45.6千克,甲的体重是42千克,乙的体重是37.2千克,丁的体重是36.8千克。
一个两位小数,最高位十位上的数是9,个位上的数是最小的自然数,十分位上的数表示6个,十分位上的数是百分位上的数的3倍。这个两位小数是( )。
【典例3】用小数的数位知识猜数
首先:确定各数位数字:已知最高位十位上的数是9;个位上的数是最小的自然数,即0;十分位上的数表示6个0.1,所以十分位上的数是6;又因为十分位上的数是百分位上的数的3倍,所以百分位上的数是6÷3=2。
再写出这个两位小数按照数位顺序,这个两位小数是90.62
90.62
【典例4】错中求解问题
淘气在计算一道加法算式时,错把3.2看成了32,算得的结果是55.7。这道题正确的结果是多少
首先:求出另一个加数因为错把3.2看成了32,算得的结果是55.7,所以另一个加数为:55.7-32=23.7。
再计算正确结果用求出的加数加上正确的3.2
正确结果为:55.7-32=23.7 23.7+3.2=26.9。
【典例5】小数加减法中和或差的变化规律
两个数的和是73.6,如果其中一个加数增加11.52,另一个加数减少8.34,那么和变成了多少
分析和的变化:一个加数增加11.52,和会增加11.52;另一个加数减少8.34,和会减少8.34。
计算变化后的和:原来两数的和是73.6
变化后的和为:73.6+11.52-8.34=76.78
【典例6】和差问题
妈妈从菜市场买回7.2千克青椒和土豆,已知青椒比土豆少2.8千克。青椒和土豆各有多少千克
图:
列式:
求土豆的重量:(7.2+2.8)÷2=5(kg)
求青椒的重量:7.2-5=2.2(kg)
【典例7】小数加减法的实际问题(画图法)
淘气家到学校的距离大约是1.8千米。这天淘气放学时向家走了0.6千米后,发现忘记带数学课本了,于是他立即原路返回取数学课本,再回家。这天放学,淘气一共走了多少千米
图:
列式:
淘气多走的路程为:0.6×2=1.2千米
淘气放学一共走的路程为:
1.8+1.2=3(千米)
【典例8】小数加减法的实际问题(消元法)
丁丁、阳阳、欣欣共有零花钱99.6元,其中丁丁、阳阳共有71.2元,丁丁、欣欣共有38.5元。丁丁有多少零花钱
方法一:
列式:
71.2+38.5-109.7(元)
109.7-99.6=10.1(元)
【典例8】小数加减法的实际问题(消元法)
丁丁、阳阳、欣欣共有零花钱99.6元,其中丁丁、阳阳共有71.2元,丁丁、欣欣共有38.5元。丁丁有多少零花钱
方法二:
列式:
99.6-71.2=28.4(元)
38.5-28.4=10.1(元)
【典例9】简便运算
找基准数法
0.9+0.99+0.999+0.9999
分析:
把0.9看成1-0.1,
0.99看成1-0.01;
0.999看成1-0.001;
0.9999看成1-0.0001。
0.9+0.99+0.999+0.9999
=(1-0.1)+(1-0.01)+(1-0.001)+(1-0.0001)
=(1+1+1+1)-(0.1+0.01+0.001+0.0001)
=4-0.1111
=3.8889
【典例9】简便运算
【典例9】简便运算
配对求和法
0.1+0.2+0.3+…+0.8+0.9
分析:
0.1和0.9配对相加得0.1+0.9=1,
0.2和0.8配对相加得0.2+0.8=1,
0.3和0.7配对相加得0.3+0.7=1,
0.4和0.6配对相加得0.4+0.6=1,
还剩下0.5。
一共有4对和为1的数,再加上0.5。
【典例9】简便运算
0.1+0.2+0.3+…+0.8+0.9
=(0.1+0.9)+(0.2+0.8)+(0.3+0.7)+(0.4+0.6)+0.5
=1×4+0.5
=4.5
模块三:完成变式训练
1.用1,3,0,7这四个数字和小数点写出含有0,但(不读出来的两位小数(每个数字只能用一次),至少写4个。
10.37 11.17 12.13 13.73 答案不唯一
2.森林运动会上,小动物们进行50米赛跑。赛跑成绩分别是8.9秒、9.3秒、8.6秒和9.9秒。它们的赛跑成绩分别是多少秒
它们的赛跑成绩分别是:
小免8.6秒,小狗8.9秒,小猫9.3秒,小猴9.9秒。
3.(1)□□□是一个三位小数,十分位上的数是千分位上的数的2倍,百分位上的数是十分位上的数的4倍,并且小数部分的数都不是0。这个三位小数是( )。
0.281
(2)ab.cd是一个两位小数,a,b,c,d分别代表0,3,6,9中的某一个数字。满足a
30.96或60.93
4.(1)丁丁在计算一道减法题时,错误地把减数3.6看成了6.3,计算出结果是0.27。这道题正确的结果是多少
先根据错误的减数和结果求出被减数,被减数为6.3+0.27=6.57
再用被减数减去正确的减数,得到正确结果为6.57-3.6=2.97。
(2)小凯在计算4.25加一个一位小数时,由于他只把数的末尾对齐,结果得到6.28。正确的得数是多少
先根据错误的计算结果和一个加数求出错误的另一个加数,6.28-4.25 =2.03.
因为是一位小数,所以正确的加数是20.3 。
那么正确的得数是4.25 +20.3 =24.55。
5.(1)两个数的和是23.8,如果其中一个加数增加7.2,那么另一个加数怎么变化,和才能比原来少4.5
求加数的变化情况一个加数增加7.2,若和不变,另一个加数应减少7.2。
现在和要比原来少4.5,所以另一个加数还要再减少4.5。
总共另一个加数要减少7.2+4.5 =11.7。
(2)在一道减法算式中,差是16.6,当被减数增加3.5,而减数减少6.8时,差是多少
被减数增加3.5,差会增加3.5;减数减少6.8,差会增加6.8。
差是166+3.5+6.8=26.9 。
6.(1)笑笑买了《趣味数独》和《小学生作文》这两本书,一共花了32.65元,《趣味数独》比《小学生作文》便宜4.65元。这两本书分别是多少元
先算出《小学生作文》价格的2倍:32.65+4.65=37.3(元)
那么《小学生作文》的价格是:37.3-2-18.65(元)
《趣味数独》的价格是:18.65-4.65=14(元)
(2)两筐苹果一共重118.76千克,如果从甲筐中拿出9.38千克苹果放入乙筐,两筐苹果就一样重。甲、乙两筐苹果分别重多少千克
两筐苹果一样重时每筐重118.76-2=59.38(千克)
甲筐原来重59.38+9.38=68.76(千克)
乙筐原来重59.38-9.38=50(千克)
7.刘叔叔拉了一车蔬菜到菜市场售卖,进入菜市场时过地磅称重,连车一起重4.5吨,到中午刚好卖了一半蔬菜,这时连车一起重2.8吨。剩下蔬菜的质量是多少 空车的质量是多少
一半蔬菜的质量是4.5-2.8=1.7(吨)
剩下蔬菜的质量等于一半蔬菜的质量,即1.7吨。
空车的质量是2.8-1.7=1.1(吨)
8.用简便方法计算
4.04+3.97+3.99+4.02 10.02+10.1+9.88+9.75
=(4.04+3.97)+(3.99 +4.02)
=8.01+8.01
=8×2+0.01×2
=16+0.02
=16.02
=(10.02+9.88)+(10.1+9.75)
=19.9+19.85
=(20-0.1)+(20-0.15)
=20+20-(0.1+0.15)
=40-0.25
=39.75
1.2+1.4+1.6+1.8+…+3.6+3.8 0.1+0.3+0.5+…+9.7+9.9。
首先求项数:n=(3.8-1.2)÷0.2+1=14
原式=14 ×(1.2+3.8)÷2
=7×5
=35
项数n=(9.9-0.1)÷0.2+1=50
原式=50×(0.1+ 9.9)÷42
=25×10
=250
