沪科版七下(2024版)8.3.1 完全平方公式 课件
文档属性
| 名称 | 沪科版七下(2024版)8.3.1 完全平方公式 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 15:52:40 | ||
图片预览







文档简介
(共23张PPT)
第8章 整式乘法与因式分解
8.3.1 完全平方公式
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
会推导完全平方公式,理解公式的结构特征,并能正确利用公式进行乘法运算。
01
了解完全平方公式的几何背景。
02
经历探索完全平方公式的过程,进一步发展符号感和推理能力。
03
通过完全平方公式的发现和推导过程,培养观察、发现、归纳、概括、猜想等探究创新能力。
04
02
新知导入
计算:
(a+1)2=(a+1)(a+1)=___________________=___________________;
(a+2)2=(a+2)(a+2)=___________________=___________________;
(a+3)2=(a+3)(a+3)=___________________=___________________;
(a-1)2=(a-1)(a-1)=___________________=___________________;
(a-2)2=(a-2)(a-2)=___________________=___________________;
(a-3)2=(a-3)(a-3)=___________________=___________________。
a2+2a+1
a2+4a+4
a2+6a+9
a2-2a+1
a2-4a+4
a2-6a+9
aa+a+a+12
aa+2a+2a+22
aa+3a+3a+32
aa-a-a+12
aa-2a-2a+22
aa-3a-3a+32
思考:观察上列等式,你有什么发现吗?
03
新知探究
猜测:(a+b)2=a2+2ab+b2 ①
(a-b)2=a2+2ab+b2 ②
你能通过计算验证这两个等式吗?
(a+b)2=aa+ab+ab+b2=a2+2ab+b2
(a-b)2=aa-ab-ab+b2=a2-2ab+b2
实际上将公式①中的b用-b代替就得出公式②.
03
新知探究
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
上面两个等式称为完全平方公式。
完全平方公式用语言叙述是:
两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
注意:两个完全平方公式可以直接使用,公式中的a,b既可代表单项式,还可代表具体的数或多项式
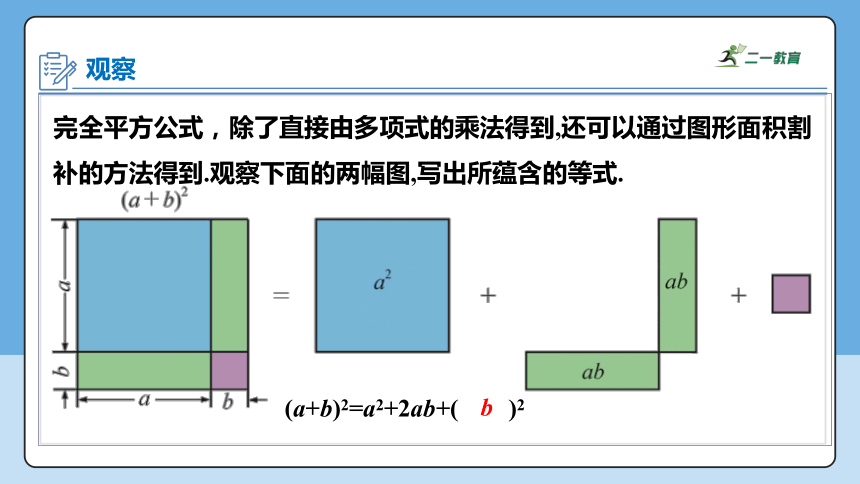
观察
完全平方公式,除了直接由多项式的乘法得到,还可以通过图形面积割补的方法得到.观察下面的两幅图,写出所蕴含的等式.
(a+b)2=a2+2ab+( )2
b
观察
(a+b)2=a2-( )+b2
2ab
03
例题探究
例1 利用乘法公式计算:(1)(2x+y)2; (2)(3a-2b)2.
解: (1)(2x+y)2 =(2x)2+2(2x)y+y2=4x2+4xy+y2
( a+b)2= a2 +2 a b+b2
(2)(3a-2b)2 =(3a)2+2(3a)2b+2b2=9a2-12ab+4b2
( a+b)2= a2 +2 a b + b2
运用公式计算,要先识别a,b在具体式子中分别表示什么.
03
例题探究
例1 利用乘法公式计算:(-m-2n)2.
解:
(-m-2n)2
=[-(m+2n)]2
=(m+2n)2
= m2+2(2n)+(2n)2
=m2+4mn+4n2
还有其它计算方法吗?
03
例题探究
例1 利用乘法公式计算:(-m-2n)2.
解:
(-m-2n)2
=(-m)2+2(-2n)+(-2n)2
=m2+4mn+4n2
1.下列多项式中是完全平方式的有( )
① ② ③ ④
A.1个
B.2个
C.3个
D.4个
04
课堂练习
【知识技能类作业】必做题:
B
2.计算(2x+1)2的结果为 ( )
A.-4x2+4x+1 B.-4x2-4x-1 C.4x2+4x+1 D.4x2-4x-1
3.若,则的值为( )
A.0 B.4 C.5 D.3或
04
课堂练习
【知识技能类作业】必做题:
C
D
04
课堂练习
【知识技能类作业】选做题:
4.若则的值为 .
5.已知是完全平方式,则 .
6.已知为实数,要使多项式是完全平方式,则k的值为 .
30
±2
04
课堂练习
【综合拓展类作业】
7.先化简,再求值:,其中.
解:
.
当时,原式.
05
课堂小结
完全平方公式用语言叙述是:
两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
注意:两个完全平方公式可以直接使用,公式中的a,b既可代表单项式,还可代表具体的数或多项式
完全平方公式
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
06
作业布置
【知识技能类作业】
1.若为任意整数,则的值总能( )
A.被整除 B.被整除 C.被整除 D.被整除
2.已知一个长方形的长为a,宽为b,它的面积为6,周长为12,则的值为( )
A.16 B.28 C.24 D.22
C
C
06
作业布置
【知识技能类作业】
3.下列图形阴影部分的面积能够直观地解释的是( )
D
A
B
C
D
06
作业布置
【综合拓展类作业】
4.已知,求下列各式的值;
(1); (2); (3).
(1)解:依题意,,
则
即.
(2)解:由(1)得,
∵,
则,
∴
06
作业布置
【综合拓展类作业】
4.已知,求下列各式的值;
(1); (2); (3).
(3)解:由(2)得,
∴,
.
或(,故舍去).
07
板书设计
完全平方公式:
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
注意:公式中的a,b既可代表单项式,还可代表具体的数或多项式
8.3.1完全平方公式
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第8章 整式乘法与因式分解
8.3.1 完全平方公式
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
会推导完全平方公式,理解公式的结构特征,并能正确利用公式进行乘法运算。
01
了解完全平方公式的几何背景。
02
经历探索完全平方公式的过程,进一步发展符号感和推理能力。
03
通过完全平方公式的发现和推导过程,培养观察、发现、归纳、概括、猜想等探究创新能力。
04
02
新知导入
计算:
(a+1)2=(a+1)(a+1)=___________________=___________________;
(a+2)2=(a+2)(a+2)=___________________=___________________;
(a+3)2=(a+3)(a+3)=___________________=___________________;
(a-1)2=(a-1)(a-1)=___________________=___________________;
(a-2)2=(a-2)(a-2)=___________________=___________________;
(a-3)2=(a-3)(a-3)=___________________=___________________。
a2+2a+1
a2+4a+4
a2+6a+9
a2-2a+1
a2-4a+4
a2-6a+9
aa+a+a+12
aa+2a+2a+22
aa+3a+3a+32
aa-a-a+12
aa-2a-2a+22
aa-3a-3a+32
思考:观察上列等式,你有什么发现吗?
03
新知探究
猜测:(a+b)2=a2+2ab+b2 ①
(a-b)2=a2+2ab+b2 ②
你能通过计算验证这两个等式吗?
(a+b)2=aa+ab+ab+b2=a2+2ab+b2
(a-b)2=aa-ab-ab+b2=a2-2ab+b2
实际上将公式①中的b用-b代替就得出公式②.
03
新知探究
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
上面两个等式称为完全平方公式。
完全平方公式用语言叙述是:
两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
注意:两个完全平方公式可以直接使用,公式中的a,b既可代表单项式,还可代表具体的数或多项式
观察
完全平方公式,除了直接由多项式的乘法得到,还可以通过图形面积割补的方法得到.观察下面的两幅图,写出所蕴含的等式.
(a+b)2=a2+2ab+( )2
b
观察
(a+b)2=a2-( )+b2
2ab
03
例题探究
例1 利用乘法公式计算:(1)(2x+y)2; (2)(3a-2b)2.
解: (1)(2x+y)2 =(2x)2+2(2x)y+y2=4x2+4xy+y2
( a+b)2= a2 +2 a b+b2
(2)(3a-2b)2 =(3a)2+2(3a)2b+2b2=9a2-12ab+4b2
( a+b)2= a2 +2 a b + b2
运用公式计算,要先识别a,b在具体式子中分别表示什么.
03
例题探究
例1 利用乘法公式计算:(-m-2n)2.
解:
(-m-2n)2
=[-(m+2n)]2
=(m+2n)2
= m2+2(2n)+(2n)2
=m2+4mn+4n2
还有其它计算方法吗?
03
例题探究
例1 利用乘法公式计算:(-m-2n)2.
解:
(-m-2n)2
=(-m)2+2(-2n)+(-2n)2
=m2+4mn+4n2
1.下列多项式中是完全平方式的有( )
① ② ③ ④
A.1个
B.2个
C.3个
D.4个
04
课堂练习
【知识技能类作业】必做题:
B
2.计算(2x+1)2的结果为 ( )
A.-4x2+4x+1 B.-4x2-4x-1 C.4x2+4x+1 D.4x2-4x-1
3.若,则的值为( )
A.0 B.4 C.5 D.3或
04
课堂练习
【知识技能类作业】必做题:
C
D
04
课堂练习
【知识技能类作业】选做题:
4.若则的值为 .
5.已知是完全平方式,则 .
6.已知为实数,要使多项式是完全平方式,则k的值为 .
30
±2
04
课堂练习
【综合拓展类作业】
7.先化简,再求值:,其中.
解:
.
当时,原式.
05
课堂小结
完全平方公式用语言叙述是:
两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
注意:两个完全平方公式可以直接使用,公式中的a,b既可代表单项式,还可代表具体的数或多项式
完全平方公式
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
06
作业布置
【知识技能类作业】
1.若为任意整数,则的值总能( )
A.被整除 B.被整除 C.被整除 D.被整除
2.已知一个长方形的长为a,宽为b,它的面积为6,周长为12,则的值为( )
A.16 B.28 C.24 D.22
C
C
06
作业布置
【知识技能类作业】
3.下列图形阴影部分的面积能够直观地解释的是( )
D
A
B
C
D
06
作业布置
【综合拓展类作业】
4.已知,求下列各式的值;
(1); (2); (3).
(1)解:依题意,,
则
即.
(2)解:由(1)得,
∵,
则,
∴
06
作业布置
【综合拓展类作业】
4.已知,求下列各式的值;
(1); (2); (3).
(3)解:由(2)得,
∴,
.
或(,故舍去).
07
板书设计
完全平方公式:
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
两个数的和(或差)的平方,等于这两个数的平方和加(或减)这两个数乘积的2倍.
注意:公式中的a,b既可代表单项式,还可代表具体的数或多项式
8.3.1完全平方公式
习题讲解书写部分
Thanks!
https://www.21cnjy.com/recruitment/home/fine
