人教A版高二下册选择性必修第三册-第七章-随机变量及其分布-大单元复习 教学设计(表格式)
文档属性
| 名称 | 人教A版高二下册选择性必修第三册-第七章-随机变量及其分布-大单元复习 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 22:18:44 | ||
图片预览


文档简介
人教A版高二下册选择性必修第三册
第七章-随机变量及其分布-大单元复习教学设计
单元课题 随机变量及其分布
本单元在高考的地位和作用分析 1.本章是概率论与数理统计的基础,涉及离散型和连续型随机变量及其分布,是高考数学的重要考点。起到承上启下的作用,衔接必修课程的概率知识,为后续的统计推断打下基础。 2.在高考中约占10%15%,是必考内容之一。高考常见题型(1)选择题:考查基本概念和性质。(2)填空题:涉及概率计算和分布函数应用。(3)解答题:综合考查随机变量的期望、方差及实际应用。 3.知识掌握 离散型随机变量:理解概念,掌握常见分布(如二项分布、泊松分布)。 连续型随机变量:理解概率密度函数,掌握正态分布及其应用。 期望与方差:会计算并理解其意义。 4.能力培养 逻辑思维:通过概率模型培养逻辑推理能力。 数据分析:提升数据处理和分析能力。 实际问题解决:应用随机变量理论解决实际问题。
单元课时计划 7.1 条件概率与全概率公式 4课时 7.2离散型随机变量及其分布列 2课时 7.3离散型随机变量的数字特征 4课时 7.4二项分布与超几何分布 4课时 7.5正态分布 2课时 总结 2课时
课程标准要求 1. 理解随机变量 掌握随机变量的概念,能够区分离散型和连续型随机变量。理解随机变量与事件的联系,并能用随机变量描述随机现象。 2. 掌握离散型随机变量及其分布列 理解离散型随机变量的分布列,掌握其性质。熟悉常见离散型随机变量的分布,如二项分布、超几何分布等,并能计算其概率。 3. 掌握连续型随机变量及其概率密度函数 理解连续型随机变量的概率密度函数,掌握其性质。熟悉常见连续型随机变量的分布,如正态分布、均匀分布等,并能计算相关概率。 理解随机变量的期望与方差 掌握期望和方差的定义及计算方法。理解期望和方差的线性性质,并能应用于实际问题。 5. 掌握正态分布及其应用 理解正态分布的定义、性质及其在实际中的应用。能利用正态分布表计算概率,解决相关问题。 6. 了解随机变量的函数及其分布 理解随机变量函数的分布,掌握简单函数的分布推导方法。 7. 应用随机变量解决实际问题 能够运用随机变量及其分布知识解决实际问题,如概率计算、期望与方差的应用等。 8. 培养数学建模能力 通过随机变量及其分布的学习,提升数学建模能力,能够将实际问题转化为数学模型并求解。 9. 培养数据分析能力 通过随机变量的学习,提升数据分析能力,能够利用概率分布分析数据并得出结论。 10. 培养逻辑思维与推理能力 通过随机变量及其分布的学习,提升逻辑思维与推理能力,能够进行复杂的概率计算与推导。
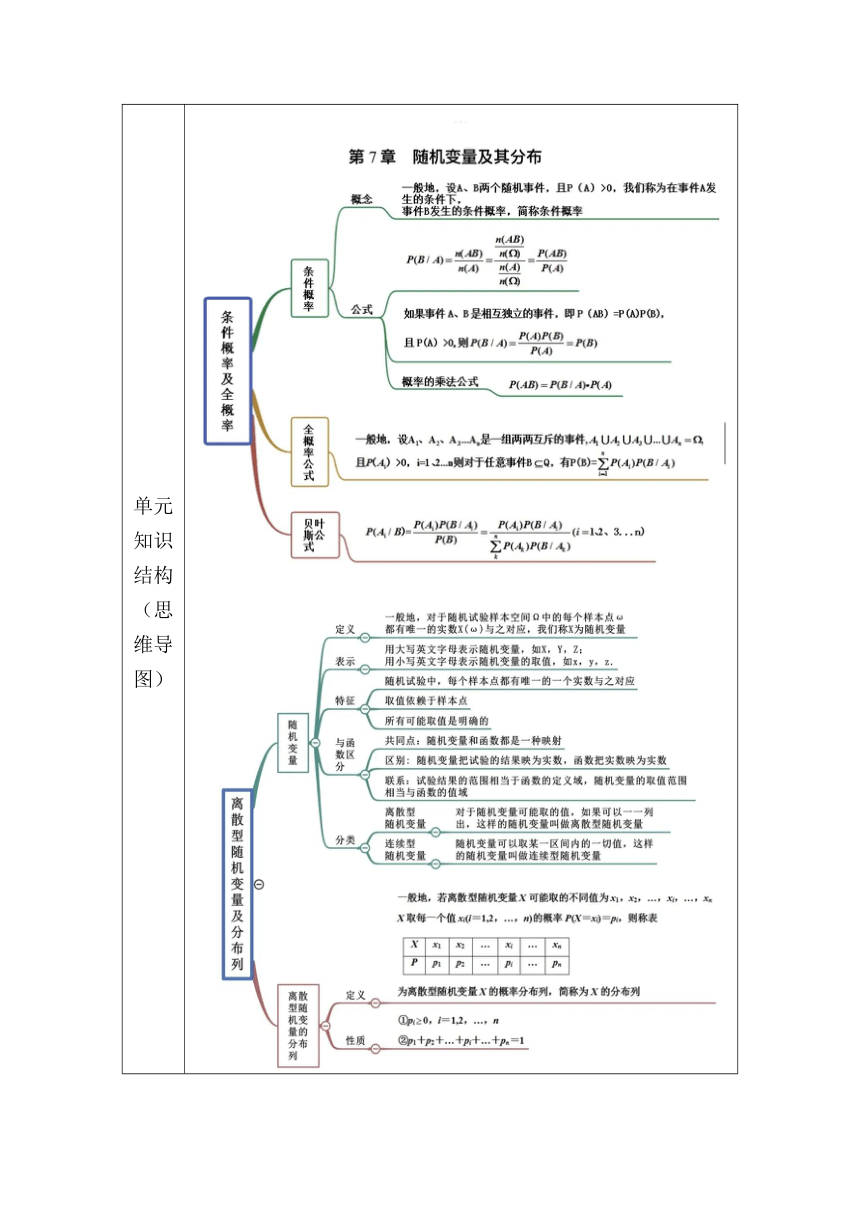
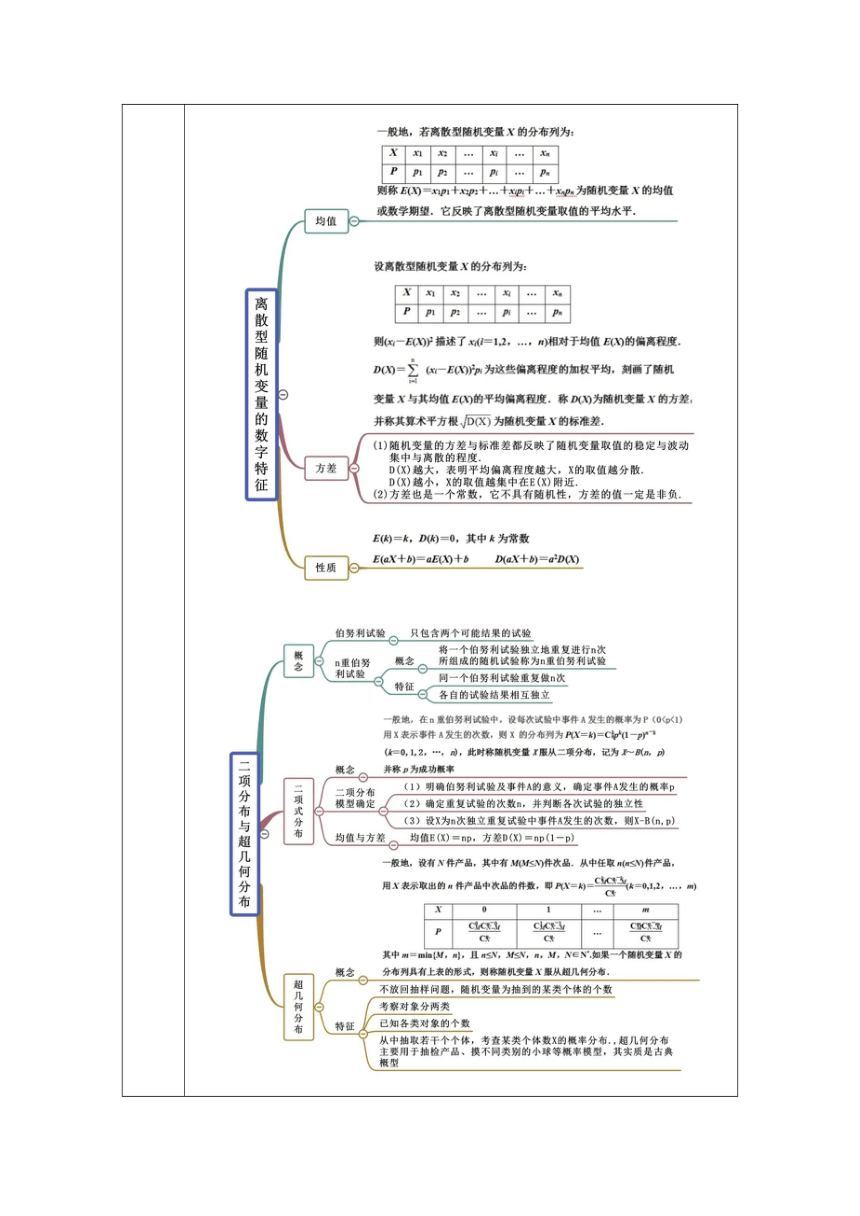
单元知识结构(思维导图)
单元教学重难点分析 一、重点内容 1. 随机变量的概念与分类 理解随机变量的定义,能够区分离散型随机变量和连续型随机变量。随机变量是概率论的核心概念,贯穿整个章节,是后续学习的基础。 2. 离散型随机变量的分布列 掌握离散型随机变量分布列的定义及性质,能够计算常见离散型随机变量的概率。离散型随机变量是概率论中最基础的类型,其分布列是描述随机现象的重要工具。 3. 常见离散型随机变量的分布 掌握二项分布、超几何分布等常见离散型随机变量的定义、性质及应用。这些分布在实际问题中应用广泛,是概率计算的重要工具。 4. 连续型随机变量的概率密度函数 理解概率密度函数的定义及性质,掌握连续型随机变量的概率计算方法。连续型随机变量是描述连续现象的基础,概率密度函数是其核心工具。 5. 正态分布及其应用 掌握正态分布的定义、性质及其在实际中的应用,能够利用正态分布表计算概率。正态分布是概率论中最重要的分布之一,广泛应用于自然科学和社会科学领域。 6. 随机变量的期望与方差 掌握期望和方差的定义、性质及计算方法,理解其在实际问题中的意义。期望和方差是描述随机变量特征的重要指标,是概率论的核心内容。 二、难点内容 1. 随机变量函数的分布 理解随机变量函数的分布,掌握其推导方法。涉及函数的变换和概率分布的转换,需要较强的数学推导能力。 2. 连续型随机变量的概率计算 理解概率密度函数的积分意义,掌握连续型随机变量概率的计算方法。连续型随机变量的概率计算涉及积分运算,对学生的数学基础要求较高。 3. 正态分布的应用 理解正态分布的性质,能够灵活应用正态分布表解决实际问题。正态分布的应用需要结合实际问题,涉及概率的标准化和查表计算,步骤较为复杂。 4. 期望与方差的性质及应用 理解期望和方差的线性性质,能够灵活应用于复杂问题。期望和方差的性质涉及较多的数学推导,应用时需要较强的逻辑思维能力。 5. 离散型与连续型随机变量的区分与联系 理解离散型与连续型随机变量的本质区别,掌握两者的联系与转换。两者在定义、性质和应用上有较大差异,容易混淆。 三、突破重难点的方法 1. 加强概念理解 通过具体例子理解随机变量、分布列、概率密度函数等概念,避免死记硬背。 2. 注重实际应用 通过实际问题(如抽奖、测量误差等)理解随机变量及其分布的应用,增强学习兴趣。 3. 强化计算训练 针对期望、方差、概率计算等内容,进行专项练习,提升计算能力。 4. 掌握正态分布表的使用 通过大量练习熟悉正态分布表的查表方法,掌握标准化公式的应用。 5. 总结常见分布的特点 对比二项分布、超几何分布、正态分布等常见分布的特点,形成系统的知识框架。 6. 培养数学建模能力 通过实际问题建模,将随机变量及其分布的知识应用于实际,提升解决问题的能力。
单元拓展知识 1. 更深入的分布类型 除了二项分布、超几何分布和正态分布外,可以拓展学习泊松分布、几何分布、指数分布等常见分布。这些分布在统计学和实际应用中有广泛用途,能够帮助学生更全面地理解随机变量的多样性。 2. 多维随机变量及其分布 引入多维随机变量(如二维随机变量)的概念,学习联合分布、边缘分布和条件分布。多维随机变量是概率论的重要内容,为后续学习统计学和机器学习奠定基础。 3. 大数定律与中心极限定理 介绍大数定律和中心极限定理的基本思想,理解其在概率论中的重要性。这两个定理是概率论的基石,能够帮助学生理解随机现象的规律性。 4. 随机变量的矩与特征函数 拓展学习随机变量的矩(如原点矩、中心矩)以及特征函数的定义和性质。矩和特征函数是描述随机变量特征的重要工具,在概率论和统计学中有广泛应用。 5. 条件期望与条件方差 引入条件期望和条件方差的概念,学习其计算方法及应用。条件期望和条件方差是概率论中的重要工具,能够帮助学生更深入地分析随机现象。 6. 随机过程初步 简单介绍随机过程的概念,如马尔可夫链、泊松过程等。随机过程是概率论的高级内容,能够帮助学生了解概率论在实际问题中的广泛应用。
单元备课使用资料计划 集体备课材料,《高中同步测控优化设计》
备注
第七章-随机变量及其分布-大单元复习教学设计
单元课题 随机变量及其分布
本单元在高考的地位和作用分析 1.本章是概率论与数理统计的基础,涉及离散型和连续型随机变量及其分布,是高考数学的重要考点。起到承上启下的作用,衔接必修课程的概率知识,为后续的统计推断打下基础。 2.在高考中约占10%15%,是必考内容之一。高考常见题型(1)选择题:考查基本概念和性质。(2)填空题:涉及概率计算和分布函数应用。(3)解答题:综合考查随机变量的期望、方差及实际应用。 3.知识掌握 离散型随机变量:理解概念,掌握常见分布(如二项分布、泊松分布)。 连续型随机变量:理解概率密度函数,掌握正态分布及其应用。 期望与方差:会计算并理解其意义。 4.能力培养 逻辑思维:通过概率模型培养逻辑推理能力。 数据分析:提升数据处理和分析能力。 实际问题解决:应用随机变量理论解决实际问题。
单元课时计划 7.1 条件概率与全概率公式 4课时 7.2离散型随机变量及其分布列 2课时 7.3离散型随机变量的数字特征 4课时 7.4二项分布与超几何分布 4课时 7.5正态分布 2课时 总结 2课时
课程标准要求 1. 理解随机变量 掌握随机变量的概念,能够区分离散型和连续型随机变量。理解随机变量与事件的联系,并能用随机变量描述随机现象。 2. 掌握离散型随机变量及其分布列 理解离散型随机变量的分布列,掌握其性质。熟悉常见离散型随机变量的分布,如二项分布、超几何分布等,并能计算其概率。 3. 掌握连续型随机变量及其概率密度函数 理解连续型随机变量的概率密度函数,掌握其性质。熟悉常见连续型随机变量的分布,如正态分布、均匀分布等,并能计算相关概率。 理解随机变量的期望与方差 掌握期望和方差的定义及计算方法。理解期望和方差的线性性质,并能应用于实际问题。 5. 掌握正态分布及其应用 理解正态分布的定义、性质及其在实际中的应用。能利用正态分布表计算概率,解决相关问题。 6. 了解随机变量的函数及其分布 理解随机变量函数的分布,掌握简单函数的分布推导方法。 7. 应用随机变量解决实际问题 能够运用随机变量及其分布知识解决实际问题,如概率计算、期望与方差的应用等。 8. 培养数学建模能力 通过随机变量及其分布的学习,提升数学建模能力,能够将实际问题转化为数学模型并求解。 9. 培养数据分析能力 通过随机变量的学习,提升数据分析能力,能够利用概率分布分析数据并得出结论。 10. 培养逻辑思维与推理能力 通过随机变量及其分布的学习,提升逻辑思维与推理能力,能够进行复杂的概率计算与推导。
单元知识结构(思维导图)
单元教学重难点分析 一、重点内容 1. 随机变量的概念与分类 理解随机变量的定义,能够区分离散型随机变量和连续型随机变量。随机变量是概率论的核心概念,贯穿整个章节,是后续学习的基础。 2. 离散型随机变量的分布列 掌握离散型随机变量分布列的定义及性质,能够计算常见离散型随机变量的概率。离散型随机变量是概率论中最基础的类型,其分布列是描述随机现象的重要工具。 3. 常见离散型随机变量的分布 掌握二项分布、超几何分布等常见离散型随机变量的定义、性质及应用。这些分布在实际问题中应用广泛,是概率计算的重要工具。 4. 连续型随机变量的概率密度函数 理解概率密度函数的定义及性质,掌握连续型随机变量的概率计算方法。连续型随机变量是描述连续现象的基础,概率密度函数是其核心工具。 5. 正态分布及其应用 掌握正态分布的定义、性质及其在实际中的应用,能够利用正态分布表计算概率。正态分布是概率论中最重要的分布之一,广泛应用于自然科学和社会科学领域。 6. 随机变量的期望与方差 掌握期望和方差的定义、性质及计算方法,理解其在实际问题中的意义。期望和方差是描述随机变量特征的重要指标,是概率论的核心内容。 二、难点内容 1. 随机变量函数的分布 理解随机变量函数的分布,掌握其推导方法。涉及函数的变换和概率分布的转换,需要较强的数学推导能力。 2. 连续型随机变量的概率计算 理解概率密度函数的积分意义,掌握连续型随机变量概率的计算方法。连续型随机变量的概率计算涉及积分运算,对学生的数学基础要求较高。 3. 正态分布的应用 理解正态分布的性质,能够灵活应用正态分布表解决实际问题。正态分布的应用需要结合实际问题,涉及概率的标准化和查表计算,步骤较为复杂。 4. 期望与方差的性质及应用 理解期望和方差的线性性质,能够灵活应用于复杂问题。期望和方差的性质涉及较多的数学推导,应用时需要较强的逻辑思维能力。 5. 离散型与连续型随机变量的区分与联系 理解离散型与连续型随机变量的本质区别,掌握两者的联系与转换。两者在定义、性质和应用上有较大差异,容易混淆。 三、突破重难点的方法 1. 加强概念理解 通过具体例子理解随机变量、分布列、概率密度函数等概念,避免死记硬背。 2. 注重实际应用 通过实际问题(如抽奖、测量误差等)理解随机变量及其分布的应用,增强学习兴趣。 3. 强化计算训练 针对期望、方差、概率计算等内容,进行专项练习,提升计算能力。 4. 掌握正态分布表的使用 通过大量练习熟悉正态分布表的查表方法,掌握标准化公式的应用。 5. 总结常见分布的特点 对比二项分布、超几何分布、正态分布等常见分布的特点,形成系统的知识框架。 6. 培养数学建模能力 通过实际问题建模,将随机变量及其分布的知识应用于实际,提升解决问题的能力。
单元拓展知识 1. 更深入的分布类型 除了二项分布、超几何分布和正态分布外,可以拓展学习泊松分布、几何分布、指数分布等常见分布。这些分布在统计学和实际应用中有广泛用途,能够帮助学生更全面地理解随机变量的多样性。 2. 多维随机变量及其分布 引入多维随机变量(如二维随机变量)的概念,学习联合分布、边缘分布和条件分布。多维随机变量是概率论的重要内容,为后续学习统计学和机器学习奠定基础。 3. 大数定律与中心极限定理 介绍大数定律和中心极限定理的基本思想,理解其在概率论中的重要性。这两个定理是概率论的基石,能够帮助学生理解随机现象的规律性。 4. 随机变量的矩与特征函数 拓展学习随机变量的矩(如原点矩、中心矩)以及特征函数的定义和性质。矩和特征函数是描述随机变量特征的重要工具,在概率论和统计学中有广泛应用。 5. 条件期望与条件方差 引入条件期望和条件方差的概念,学习其计算方法及应用。条件期望和条件方差是概率论中的重要工具,能够帮助学生更深入地分析随机现象。 6. 随机过程初步 简单介绍随机过程的概念,如马尔可夫链、泊松过程等。随机过程是概率论的高级内容,能够帮助学生了解概率论在实际问题中的广泛应用。
单元备课使用资料计划 集体备课材料,《高中同步测控优化设计》
备注
