人教A版高二下册选择性必修第三册7.1.1条件概率 课件(共28张PPT)
文档属性
| 名称 | 人教A版高二下册选择性必修第三册7.1.1条件概率 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 456.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-03-31 22:29:12 | ||
图片预览







文档简介
(共28张PPT)
7.1.1 条件概率
第7章《随机变量及其分布》
人教A版2019选择性必修第三册
1.结合古典概型,了解条件概率的概念,能计算简单随机事件的条件概率.
2.结合古典概型,了解条件概率与事件的独立性的关系.
3.结合古典概型,会利用乘法公式计算概率.
学习目标
概率是随机事件发生可能性大小的度量.在必修课程的概率学习中,我们结合古典概型,研究了简单随机事件及其概率的计算方法,并讨论了概率的一些性质.本章将在此基础上,结合古典概型,研究随机事件的条件概率,建立概率的乘法公式和全概率公式,并用它们计算较复杂事件的概率.
为了利用数学工具,并以简洁、统一的形式研究随机试验的规律,本章我们还将把随机试验的结果数量化,引入随机变量的概念.对离散型随机变量,我们主要研究其分布列及数字特征,并对二项分布、超几何分布进行重点研究.对于连续型随机变量,我们只研究服从正态分布的情况.通过用随机变量描述和分析随机试验,解决一些简单的实际问题,进一步体会概率模型的作用及概率思想和方法的特点.
环节一:创设情境,引入课题
如果事件A与B不独立,如何表示积事件AB的概率呢?下面我们从具体问题入手.
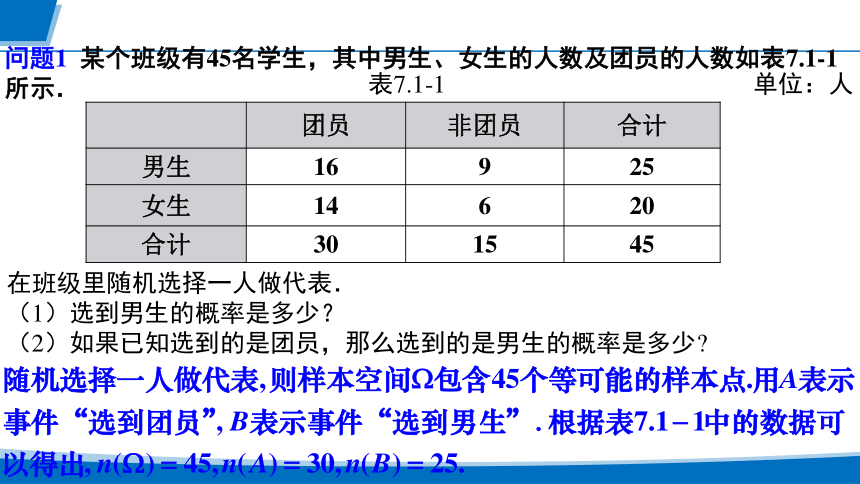
问题1 某个班级有45名学生,其中男生、女生的人数及团员的人数如表7.1-1所示.
表7.1-1 单位:人
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少
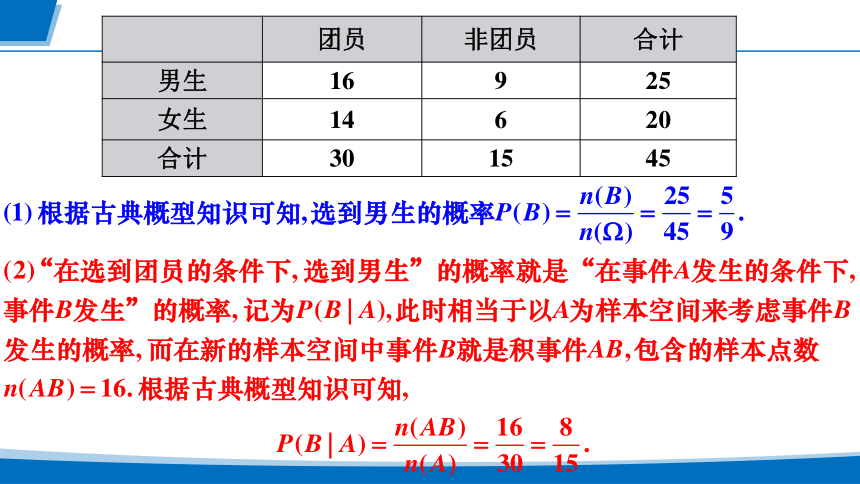
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
问题2 假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭.随机选择一个家庭,那么
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
环节二:观察分析,感知概念
问题2 假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭.随机选择一个家庭,那么
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
A
B
AB
图7.1-1
这个结论对于一般的古典概型仍然成立.事实上,如图7.1-1所示,若已知事件A发生,则A成为样本空间.此时,事件B发生的概率是AB包含的样本点数与A包含的样本点数的比值,即
探究
环节三:抽象概括,形成概念
我们称上式为概率的乘法公式(multiplication formula).
环节四:辨析理解,深化概念
例 1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是积事件的概率,问题(2)就是条件概率.可以先求积事件的概率,再用条件概率公式求条件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
环节五:课堂练习,巩固运用
例 1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
例 1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
例 1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗
分析:要知道中奖概率是否与抽奖次序有关,只要考察甲、乙、丙3名同学的中奖概率是否相等.因为只有1张有奖,所以“乙中奖”等价于“甲没中奖且乙中奖”,“丙中奖”等价于“甲和乙都没中奖”,利用乘法公式可求出乙、丙中奖的概率.
事实上,在抽奖问题中,无论是放回随机抽取还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
分析:最后1位密码“不超过2次就按对”等价于“第1次按对,或者第1次按错但第2次按对”.因此,可以先把复杂事件用简单事件表示,再利用概率的性质求解.
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
1. 条件概率:
在事件A发生的条件下,事件B发生的条件概率,简称条件概率,记作
由条件概率公式可得
2. 乘法公式:
当P(A)>0 时,当且仅当事件A与B相互独立时,有P(B|A)=P(B)成立.
环节六:归纳总结,反思提升
3.条件概率需注意以下几点
(1)事件B在事件A已发生这个附加条件下的概率与没有这个附加条件的概率是不同的.
(2)所谓条件概率,是当试验结果的一部分信息已知(即在原随机试验的条件下,再加上一定的条件),求另一事件在此条件下的概率.
(3)已知事件A发生,在此条件下B发生,相当于AB发生,求P(B|A)时,可把A看做新的基本事件空间来计算B发生的概率,
4.如何理解条件概率公式?
(1)前提条件:P(A)>0
(2)条件概率公式揭示了条件概率P(B|A)与事件P(A),P(AB)三者之间的关系,由条件概率公式可以解决下列两类问题.
①已知P(A),P(AB),求P(B|A);
②已知P(A),P(B|A),求P(AB).
环节七:目标检测,作业布置
完成教材:
第48页练习1,2题,
习题7.1第1,2,3,6,9,10题
练习 第48页
2.从一副不含大小王的52张扑克牌中,每次从中随机抽出1张扑克牌,抽出的牌不再放回.已知第1次抽到A牌,求第2次抽到A牌的概率.
设“第1次抽到A”为事件B,“第2次抽到A”为事件C,则“第1次和第2次都抽到A”为事件BC.
3.袋子中有10个大小相同的小球,其中7个白球,3个黑球.每次从袋子中随机摸出1个球,摸出的球不再放回.求:
(1)在第1次摸到白球的条件下,第2次摸到白球的概率;
(2)两次都摸到白球的概率.
7.1.1 条件概率
第7章《随机变量及其分布》
人教A版2019选择性必修第三册
1.结合古典概型,了解条件概率的概念,能计算简单随机事件的条件概率.
2.结合古典概型,了解条件概率与事件的独立性的关系.
3.结合古典概型,会利用乘法公式计算概率.
学习目标
概率是随机事件发生可能性大小的度量.在必修课程的概率学习中,我们结合古典概型,研究了简单随机事件及其概率的计算方法,并讨论了概率的一些性质.本章将在此基础上,结合古典概型,研究随机事件的条件概率,建立概率的乘法公式和全概率公式,并用它们计算较复杂事件的概率.
为了利用数学工具,并以简洁、统一的形式研究随机试验的规律,本章我们还将把随机试验的结果数量化,引入随机变量的概念.对离散型随机变量,我们主要研究其分布列及数字特征,并对二项分布、超几何分布进行重点研究.对于连续型随机变量,我们只研究服从正态分布的情况.通过用随机变量描述和分析随机试验,解决一些简单的实际问题,进一步体会概率模型的作用及概率思想和方法的特点.
环节一:创设情境,引入课题
如果事件A与B不独立,如何表示积事件AB的概率呢?下面我们从具体问题入手.
问题1 某个班级有45名学生,其中男生、女生的人数及团员的人数如表7.1-1所示.
表7.1-1 单位:人
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
在班级里随机选择一人做代表.
(1)选到男生的概率是多少?
(2)如果已知选到的是团员,那么选到的是男生的概率是多少
团员 非团员 合计
男生 16 9 25
女生 14 6 20
合计 30 15 45
问题2 假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭.随机选择一个家庭,那么
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
环节二:观察分析,感知概念
问题2 假定生男孩和生女孩是等可能的,现考虑有两个小孩的家庭.随机选择一个家庭,那么
(1)该家庭中两个小孩都是女孩的概率是多大?
(2)如果已经知道这个家庭有女孩,那么两个小孩都是女孩的概率又是多大?
A
B
AB
图7.1-1
这个结论对于一般的古典概型仍然成立.事实上,如图7.1-1所示,若已知事件A发生,则A成为样本空间.此时,事件B发生的概率是AB包含的样本点数与A包含的样本点数的比值,即
探究
环节三:抽象概括,形成概念
我们称上式为概率的乘法公式(multiplication formula).
环节四:辨析理解,深化概念
例 1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
分析:如果把“第1次抽到代数题”和“第2次抽到几何题”作为两个事件,那么问题(1)就是积事件的概率,问题(2)就是条件概率.可以先求积事件的概率,再用条件概率公式求条件概率;也可以先求条件概率,再用乘法公式求积事件的概率.
环节五:课堂练习,巩固运用
例 1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
例 1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
例 1 在5道试题中有3道代数题和2道几何题,每次从中随机抽出1道题,抽出的题不再放回.求:
(1)第1次抽到代数题且第2次抽到几何题的概率;
(2)在第1次抽到代数题的条件下,第2次抽到几何题的概率.
例2 已知3张奖券中只有1张有奖,甲、乙、丙3名同学依次不放回地各随机抽取1张.他们中奖的概率与抽奖的次序有关吗
分析:要知道中奖概率是否与抽奖次序有关,只要考察甲、乙、丙3名同学的中奖概率是否相等.因为只有1张有奖,所以“乙中奖”等价于“甲没中奖且乙中奖”,“丙中奖”等价于“甲和乙都没中奖”,利用乘法公式可求出乙、丙中奖的概率.
事实上,在抽奖问题中,无论是放回随机抽取还是不放回随机抽取,中奖的概率都与抽奖的次序无关.
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
分析:最后1位密码“不超过2次就按对”等价于“第1次按对,或者第1次按错但第2次按对”.因此,可以先把复杂事件用简单事件表示,再利用概率的性质求解.
例3 银行储蓄卡的密码由6位数字组成.某人在银行自助取款机上取钱时,忘记了密码的最后1位数字.求:
(1)任意按最后1位数字,不超过2次就按对的概率;
(2)如果记得密码的最后1位是偶数,不超过2次就按对的概率.
1. 条件概率:
在事件A发生的条件下,事件B发生的条件概率,简称条件概率,记作
由条件概率公式可得
2. 乘法公式:
当P(A)>0 时,当且仅当事件A与B相互独立时,有P(B|A)=P(B)成立.
环节六:归纳总结,反思提升
3.条件概率需注意以下几点
(1)事件B在事件A已发生这个附加条件下的概率与没有这个附加条件的概率是不同的.
(2)所谓条件概率,是当试验结果的一部分信息已知(即在原随机试验的条件下,再加上一定的条件),求另一事件在此条件下的概率.
(3)已知事件A发生,在此条件下B发生,相当于AB发生,求P(B|A)时,可把A看做新的基本事件空间来计算B发生的概率,
4.如何理解条件概率公式?
(1)前提条件:P(A)>0
(2)条件概率公式揭示了条件概率P(B|A)与事件P(A),P(AB)三者之间的关系,由条件概率公式可以解决下列两类问题.
①已知P(A),P(AB),求P(B|A);
②已知P(A),P(B|A),求P(AB).
环节七:目标检测,作业布置
完成教材:
第48页练习1,2题,
习题7.1第1,2,3,6,9,10题
练习 第48页
2.从一副不含大小王的52张扑克牌中,每次从中随机抽出1张扑克牌,抽出的牌不再放回.已知第1次抽到A牌,求第2次抽到A牌的概率.
设“第1次抽到A”为事件B,“第2次抽到A”为事件C,则“第1次和第2次都抽到A”为事件BC.
3.袋子中有10个大小相同的小球,其中7个白球,3个黑球.每次从袋子中随机摸出1个球,摸出的球不再放回.求:
(1)在第1次摸到白球的条件下,第2次摸到白球的概率;
(2)两次都摸到白球的概率.
